Security Analysis of Network Protocols John Mitchell Stanford

Security Analysis of Network Protocols John Mitchell Stanford University

Computer Security Research ? Semantic Assurance Cyber Strategy Auto Forensics OODA Web Services Intrusion Tolerance Privacy Autonomic Response Cyber Survivable Security of Control Panel Network Mobile Infrastructures IA Agents Malicious Sensors Code Protective Intrusion Situational Mechanisms Detection Understanding Open Source Crypto Strategies Law Enforcemen Composable Course t Policy Trust of Action Physical Dynamic Projection Security Coalitions Cyber Sensor Exploitation ? Lifecycle Attacks Formalized Design Insider MDS/MLS

Security Protocols u. Challenge-response • ISO 9798 -1, 2, 3; Needham-Schroeder, … u. Authentication • Kerberos u. Key Exchange • SSL handshake, IKE, JFK, IKEv 2, u. Wireless and mobile computing • Mobile IP, WEP, 802. 11 i u. Electronic commerce • Contract signing, SET, electronic cash, …

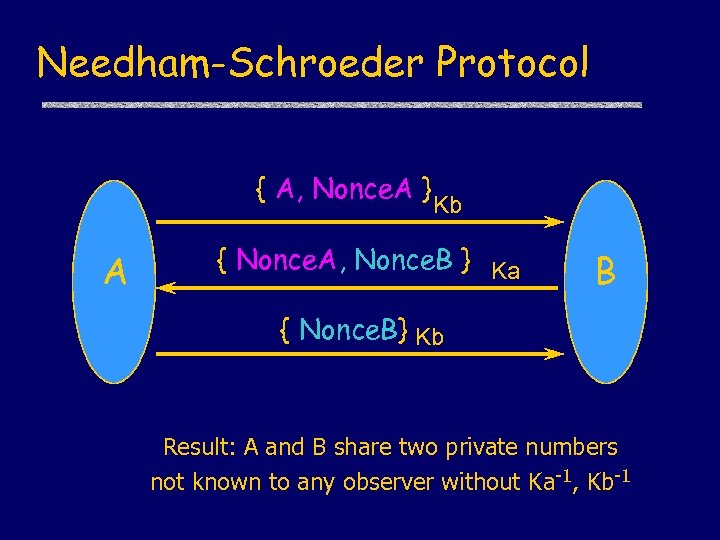Needham-Schroeder Protocol { A, Nonce. A } A Kb { Nonce. A, Nonce. B } Ka B { Nonce. B} Kb Result: A and B share two private numbers not known to any observer without Ka-1, Kb-1

Anomaly in Needham-Schroeder [Lowe] { A, Na } Ke A E { Na, Nb } Ka { Nb } Ke Evil agent E tricks honest A into revealing private key Nb from B. Evil E can then fool B. { Na, Nb } { A, Na } Ka B Kb

Needham-Schroeder Lowe { A, Nonce. A } A Kb { Nonce. A, B, Nonce. B } { Nonce. B} Kb Authentication? Secrecy? Replay attack Forward secrecy? Denial of service? Identity protection? Ka B

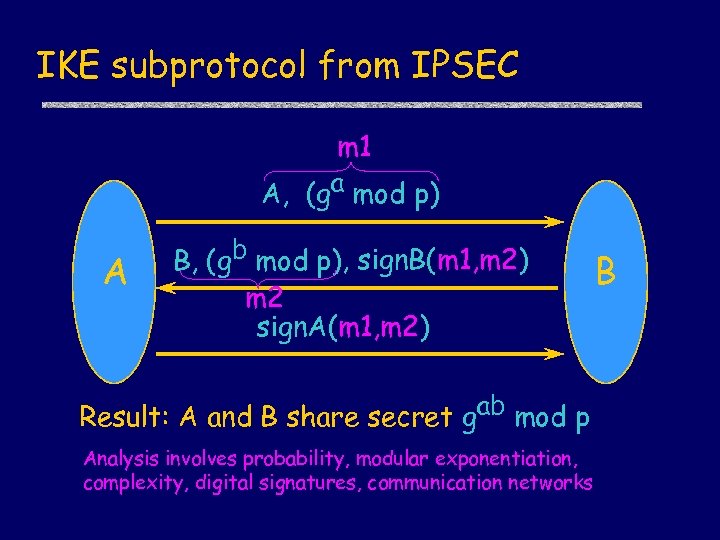IKE subprotocol from IPSEC m 1 A, (ga mod p) A B, (gb mod p), sign. B(m 1, m 2) m 2 sign. A(m 1, m 2) Result: A and B share secret gab mod p Analysis involves probability, modular exponentiation, complexity, digital signatures, communication networks B

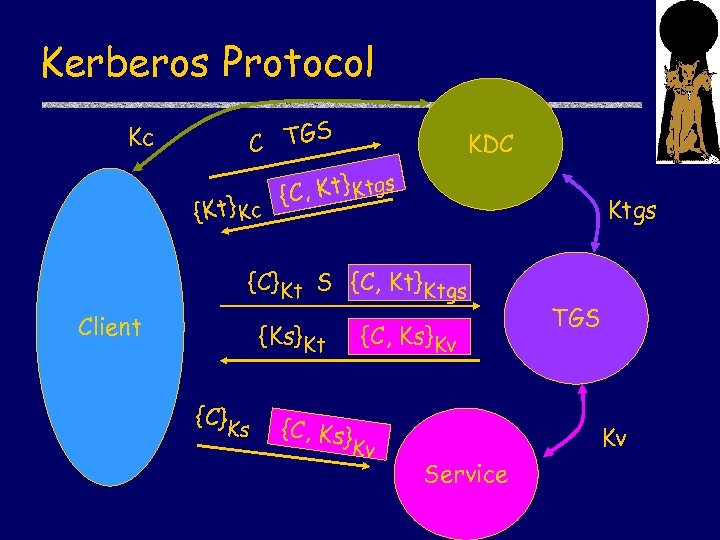Kerberos Protocol S C TG Kc {Kt} Kc KDC 1 T Kt}t s {C, icke Ktgs {C}Kt S {C, Kt}Ktgs Ticket 1 Client {Ks}Kt {C}K s {C, Ks}Kv Ticket 2 {Ti, cket 2 C Ks} Kv TGS Kv Service

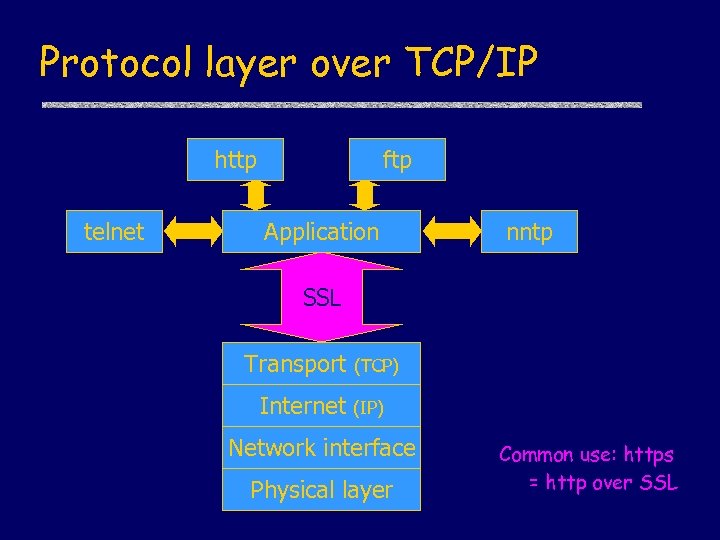Protocol layer over TCP/IP http telnet ftp Application nntp SSL Transport Internet (TCP) (IP) Network interface Physical layer Common use: https = http over SSL

Handshake Protocol Client. Hello C S C, Ver. C, Suite. C, NC Server. Hello S C Ver. S, Suite. S, NS, sign. CA{ S, KS } Client. Verify C S sign. CA{ C, VC } { Ver. C, Secret. C } KS S sign. C { Hash( Master(NC, NS, Secret. C) + Pad 2 + Hash(Msgs + C + Master(NC, NS, Secret. C) + Pad 1)) } (Change to negotiated cipher) Server. Finished S C { Hash( Master(NC, NS, Secret. C) + Pad 2 + Hash( Msgs + S + Master(NC, NS, Secret. C) + Pad 1)) } Master(NC, NS, Secret. C) Client. Finished C S { Hash( Master(NC, NS, Secret. C) + Pad 2 + Hash( Msgs + C + Master(NC, NS, Secret. C) + Pad 1)) } Master(N , Secret ) C S C

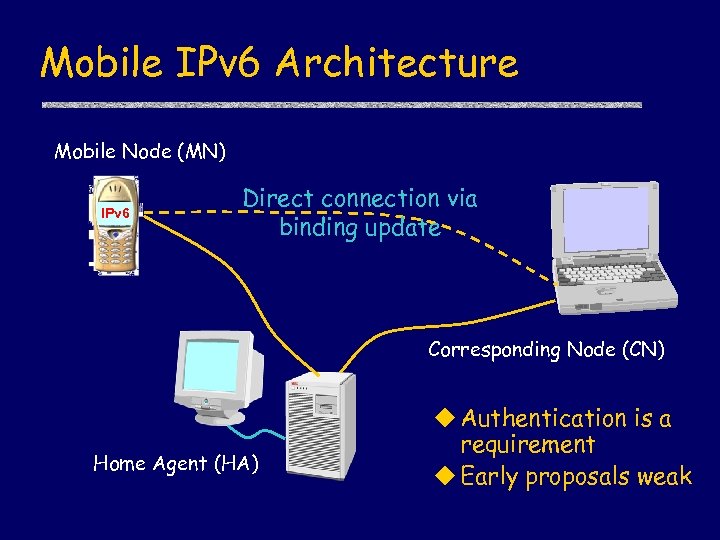Mobile IPv 6 Architecture Mobile Node (MN) IPv 6 Direct connection via binding update Corresponding Node (CN) Home Agent (HA) u Authentication is a requirement u Early proposals weak

Wireless Authentication: Robust Security Network Association u. Pre-RSNA Poor Security • 802. 11 Authentication • Wired Equivalent Protocol • CRC MIC (Message Integrity Code) u. RSNA Better Security • 802. 1 x Authentication • Key Management • Improved MIC scheme, data encryption

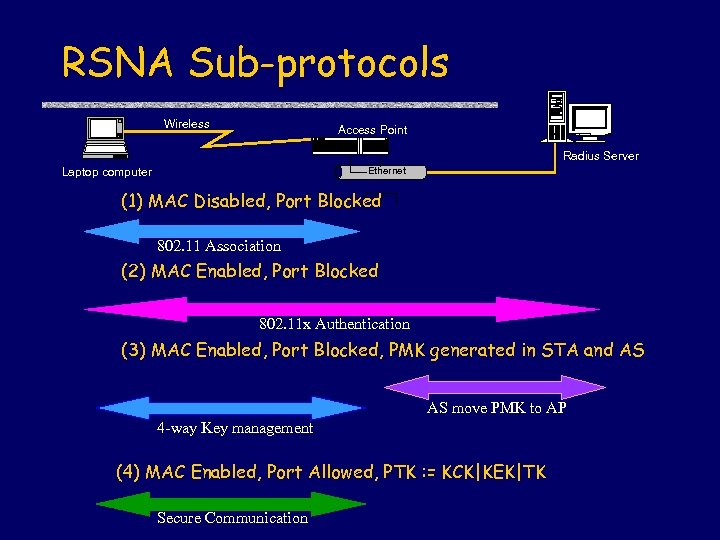RSNA Sub-protocols Wireless Access Point Radius Server Ethernet Laptop computer (1) MAC Disabled, Port Blocked 802. 11 Association (2) MAC Enabled, Port Blocked 802. 11 x Authentication (3) MAC Enabled, Port Blocked, PMK generated in STA and AS AS move PMK to AP 4 -way Key management (4) MAC Enabled, Port Allowed, PTK : = KCK|KEK|TK Secure Communication

Optimistic contract signing I am going to sign the contract A Here is my signature B Here is my signature u. Trusted third party can force contract • Third party can declare contract binding if presented with first two messages.

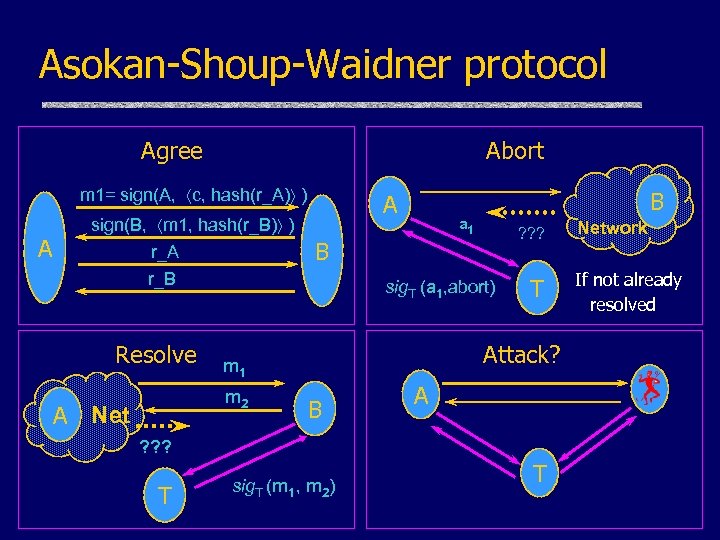Asokan-Shoup-Waidner protocol Agree Abort m 1= sign(A, c, hash(r_A) ) A sign(B, m 1, hash(r_B) ) r_A A Resolve ? ? ? sig. T (a 1, abort) T Attack? m 1 m 2 A Net a 1 B r_B B B A ? ? ? T sig. T (m 1, m 2) T Network If not already resolved

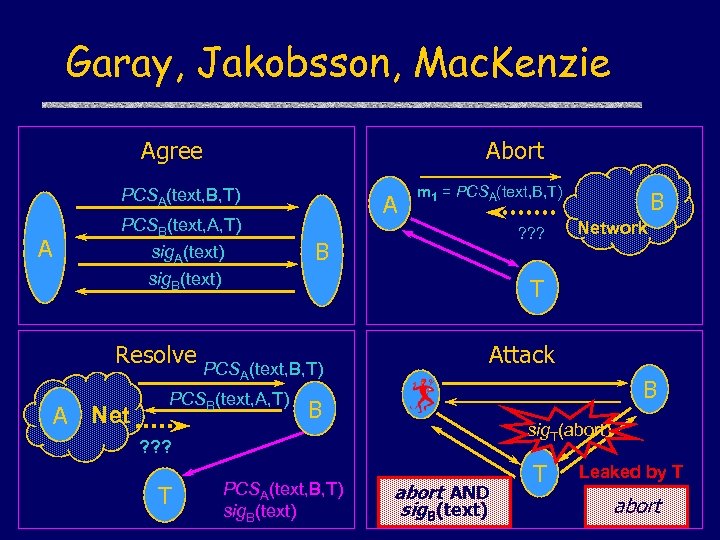Garay, Jakobsson, Mac. Kenzie Agree Abort PCSA(text, B, T) A PCSB(text, A, T) sig. A(text) A m 1 = PCSA(text, B, T) ? ? ? B sig. B(text) A(text, B, T) PCSB(text, A, T) Attack B B sig. T(abort) ? ? ? T Network T Resolve PCS A Net B PCSA(text, B, T) sig. B(text) abort AND sig. B(text) T Leaked by T abort

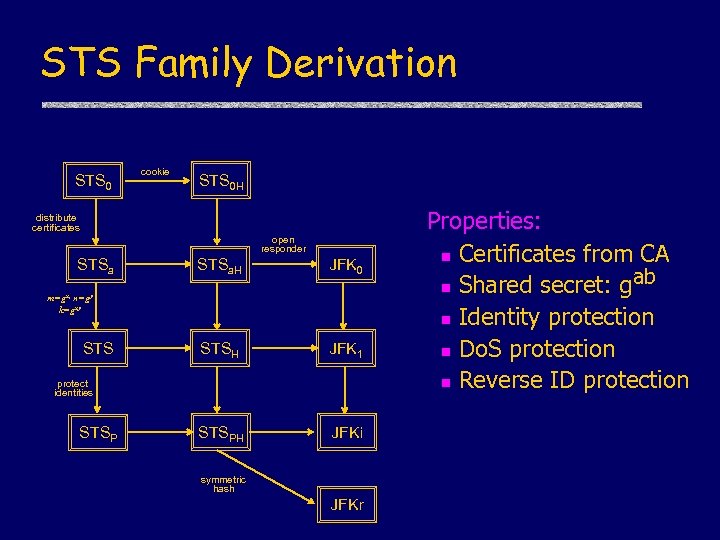STS Family Derivation STS 0 cookie STS 0 H distribute certificates open responder STSa. H JFK 0 STSH JFK 1 STSPH JFKi m=gx, n=gy k=gxy STS protect identities STSP symmetric hash JFKr Properties: n Certificates from CA ab n Shared secret: g n Identity protection n Do. S protection n Reverse ID protection

Protocol Analysis u. Computational approaches (insightful, no tools…) • Proof methods of Bellare-Rogaway, Mauer • Canetti, Backes-Pfitzmann-Waidner u BAN and related axiomatic approaches u. Methods grounded in symbolic execution • Assume perfect cryptography • Protocol determines set of traces – Arbitrary number of principals plus intruder • Enumerate, search, or reason about this set

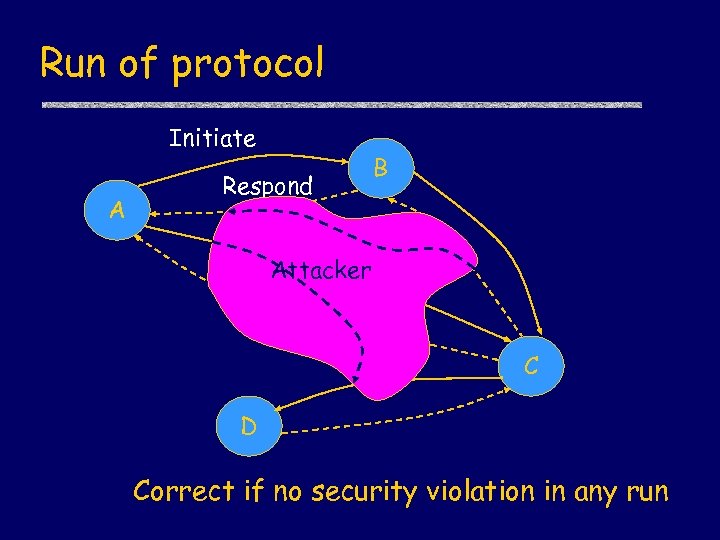Run of protocol Initiate A Respond B Attacker C D Correct if no security violation in any run

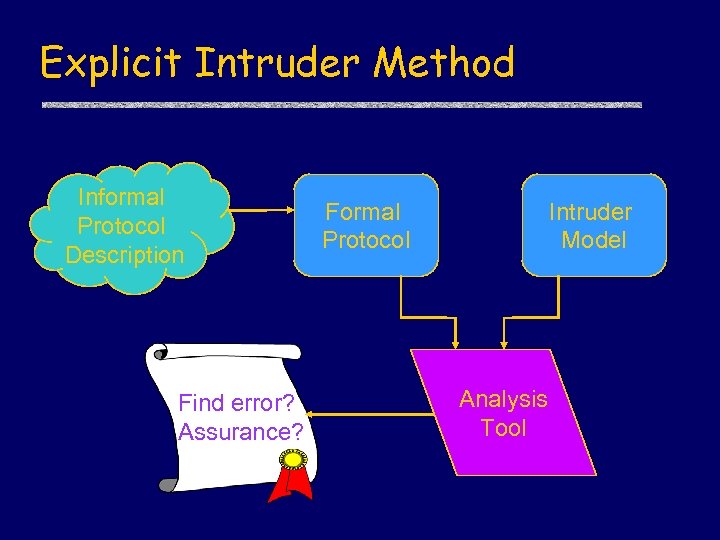Explicit Intruder Method Informal Protocol Description Find error? Assurance? Formal Protocol Intruder Model Analysis Tool

Automated Finite-State Analysis u. Define finite-state system • Bound on number of steps • Finite number of participants • Nondeterministic adversary with finite options u. Pose correctness condition • Can be simple: authentication and secrecy • Can be complex: contract signing u. Exhaustive search using “verification” tool • Error in finite approximation Error in protocol • No error in finite approximation ? ? ?

State Reduction on N-S Protocol

Model Checking Studies u. Standard academic benchmarks • Needham-Schroeder, TMN, Kerberos- u. Realistic network protocols • SSL 3. 0, with resumption protocol u. Contract signing protocols • Asokan-Shoup-Waidner, Garay-Jakobsson-Mac. Kenzie u. Wireless networking • Authenticated Mobile IPv 6 • 802. 11 i

CS 259 Term Projects i. KP protocol family Electronic voting IEEE 802. 11 i wireless Onion Routing handshake protocol Secure Ad-Hoc Distance Vector Routing An Anonymous Fair Exchange E-commerce Protocol Secure Internet Live Conferencing Windows file-sharing protocols XML Security Electronic Voting Key Infrastructure

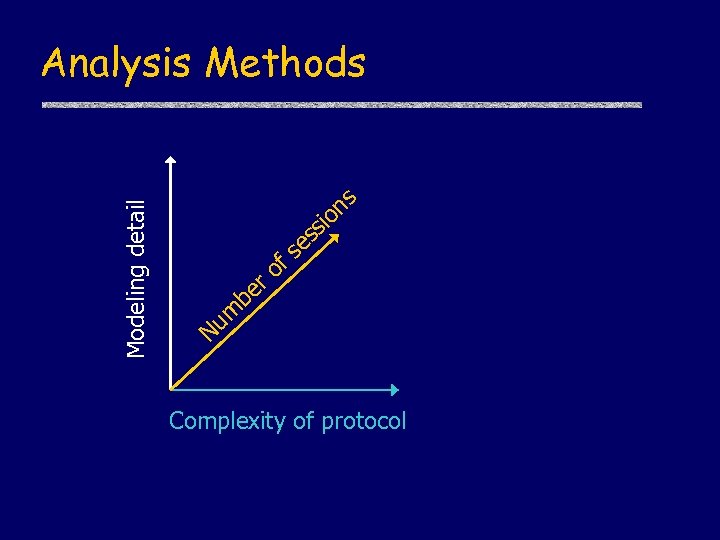Modeling detail Analysis Methods ns o i ss e er b fs o um N Complexity of protocol

High Hand proofs Poly-time calculus Multiset rewriting with Spi-calculus Athena Paulson NRL Strand spaces BAN logic Low Modeling detail Protocol analysis spectrum Protocol logic Low Model checking FDR Protocol complexity High Mur

Protocol derivation u. Protocol derivation • Build security protocols by combining parts from standard sub-protocols. u. Proof of correctness • Prove protocols correct using logic that follows steps of derivation.

Example u. Construct protocol with properties: • • Shared secret Authenticated Identity Protection Do. S Protection u. Design requirements for IKE, JFK, IKEv 2 (IPSec key exchange protocol)

Component 1 u. Diffie-Hellman A B: ga B A: gb • Shared secret (with someone) – A deduces: Knows(Y, gab) (Y = A) ۷ Knows(Y, b) • Authenticated • Identity Protection • Do. S Protection

Component 2 u. Challenge Response: A B: m, A B A: n, sig. B {m, n, A} A B: sig. A {m, n, B} • Shared secret (with someone) • Authenticated – A deduces: Received (B, msg 1) Λ Sent (B, msg 2) • Identity Protection • Do. S Protection

Composition u. ISO 9798 -3 protocol: A B: ga, A B A: gb, sig. B {ga, gb, A} A B: sig. A {ga, gb, B} • • Shared secret: gab Authenticated Identity Protection Do. S Protection m : = ga n : = gb

Refinement u. Encrypt signatures: A B: ga, A B A: gb, EK {sig. B {ga, gb, A}} A B: EK {sig. A {ga, gb, B}} • • Shared secret: gab Authenticated Identity Protection Do. S Protection

Transformation u. Use cookie: JFK core protocol A B: ga, A B A: gb, hash. KB {gb, ga} A B: ga, gb, hash. KB {gb, ga} EK {sig. A {ga, gb, B}} B A: gb, EK {sig. B {ga, gb, A}} • • Shared secret: gab Authenticated Identity Protection Do. S Protection

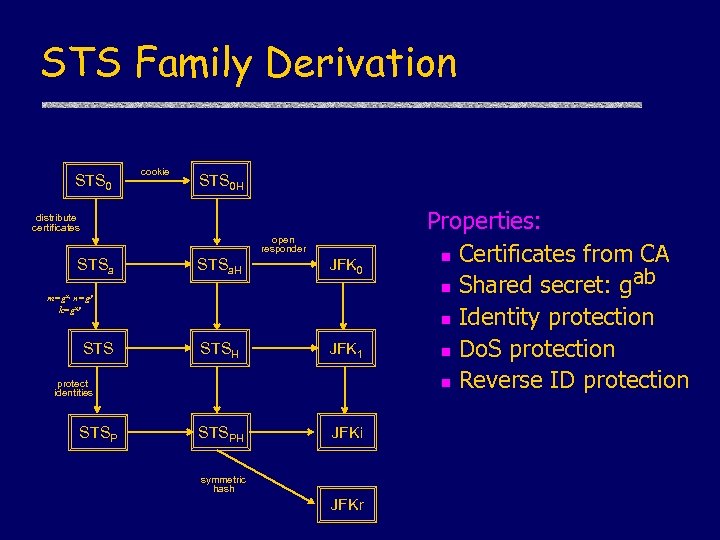STS Family Derivation STS 0 cookie STS 0 H distribute certificates open responder STSa. H JFK 0 STSH JFK 1 STSPH JFKi m=gx, n=gy k=gxy STS protect identities STSP symmetric hash JFKr Properties: n Certificates from CA ab n Shared secret: g n Identity protection n Do. S protection n Reverse ID protection

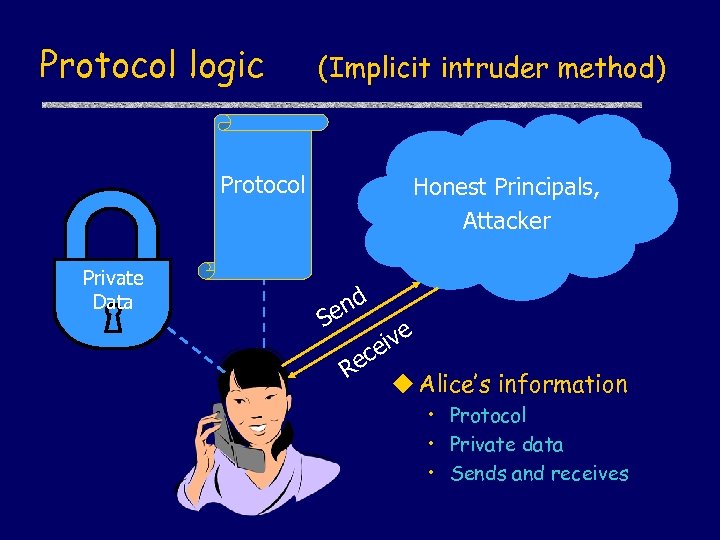Protocol logic (Implicit intruder method) Protocol Private Data Honest Principals, Attacker nd e S ec R ive e u Alice’s information • Protocol • Private data • Sends and receives

Intuition u. Reason about local information • • I chose a new number I sent it out encrypted I received it decrypted Therefore: someone decrypted it u. Incorporate knowledge about protocol • Protocol: Server only sends m if it got m’ • If server not corrupt and I receive m signed by server, then server received m’

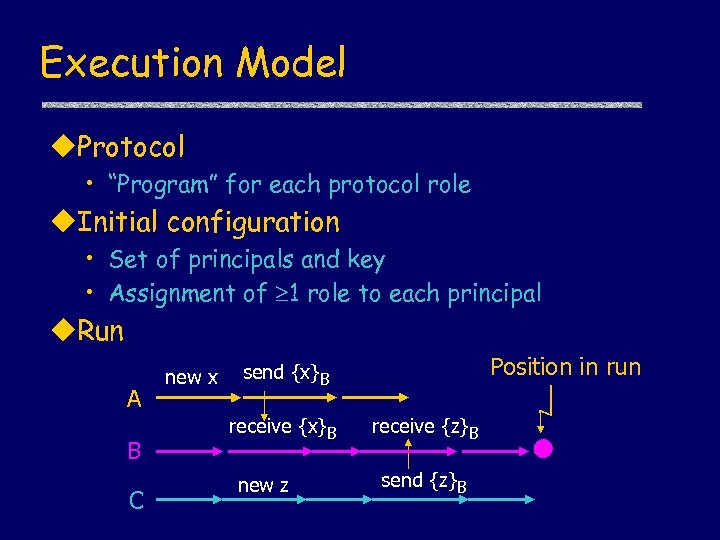Execution Model u. Protocol • “Program” for each protocol role u. Initial configuration • Set of principals and key • Assignment of 1 role to each principal u. Run A B C new x Position in run send {x}B receive {x}B new z receive {z}B send {z}B

Formulas true at a position in run u. Action formulas a : : = Send(P, m) | Receive (P, m) | New(P, t) | Decrypt (P, t) | Verify (P, t) u. Formulas : : = a | Has(P, t) | Fresh(P, t) | Honest(N) | Contains(t 1, t 2) | | 1 2 | x | | u. Example After(a, b) = (b a)

Modal Formulas u. After actions, postcondition [ actions ] P where P = princ, role id u. Before/after assertions [ actions ] P u. Composition rule [S]P [T]P [ ST ] P Note: same P in all formulas

Proof System u. Sample Axioms: • Reasoning about knowledge: – Has(A, enc. X{m}) Has(A, K) Has(A, m) – Has(A, {m, n}) Has(A, m) Has(A, n) • Reasoning about crypto primitives: – Honest(X) Decrypt(Y, enc. X{m}) X=Y – Honest(X) Verify(Y, sig. X{m}) m’ ( Send(X, m’) Contains(m’, sig. X{m}) u. Inference Rule • Persistence rules, … • Honesty/Invariance rule u. Soundness Theorem: • Every provable formula is valid

Bidding conventions (motivation) u. Blackwood response to 4 NT – 5§ : 0 or 4 aces – 5¨ : 1 ace – 5© : 2 aces – 5ª : 3 aces u. Reasoning • If my partner is following Blackwood, then if she bid 5©, she must have 2 aces

Correctness of NSL u. Bob knows he’s talking to Alice [ recv encrypt( Key(B), A, m ); new n; msg 1 send encrypt( Key(A), m, B, n ); recv encrypt( Key(B), n ) ]B msg 3 Honest(A) Csent(A, msg 1) Csent(A, msg 3) where Csent(A, …) Created(A, …) Sent(A, …)

Composition Rules u. Prove assertions from invariants |- […]P u. Invariant weakening rule |- […]P ’ |- […]P If combining protocols, extend assertions to combined invariants u. Prove invariants from protocol Q Q’ Use honesty (invariant) rule to show that both protocols preserve assumed invariants

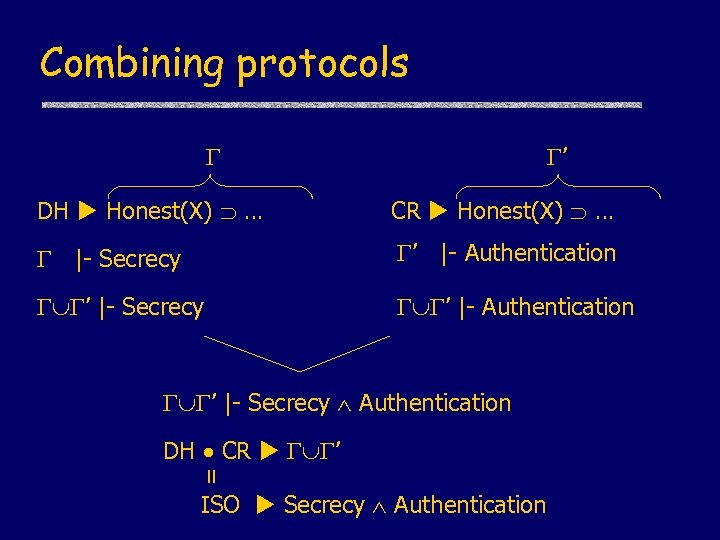Combining protocols ’ DH Honest(X) … CR Honest(X) … |- Secrecy ’ |- Authentication ’ |- Secrecy Authentication = DH CR ’ ISO Secrecy Authentication

Protocol Templates u. Protocols with function variables instead of specific operations • One template can be instantiated to many protocols u. Advantages: • proof reuse • design principles/patterns

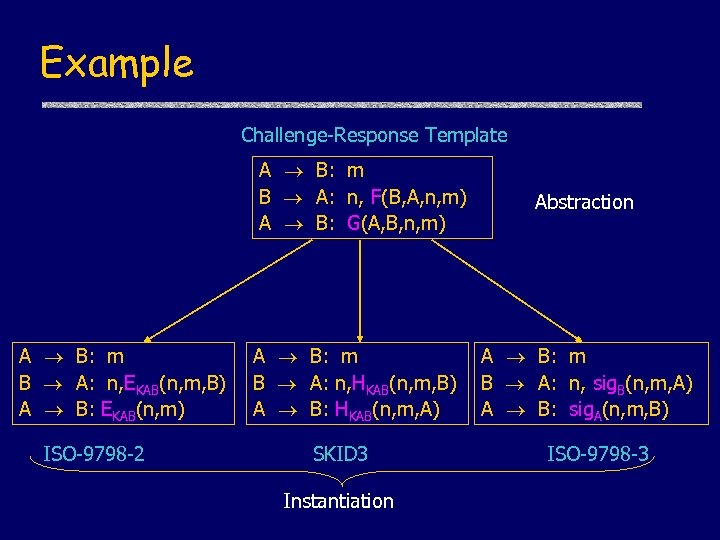Example Challenge-Response Template A B: m B A: n, F(B, A, n, m) A B: G(A, B, n, m) A B: m B A: n, EKAB(n, m, B) A B: EKAB(n, m) ISO-9798 -2 A B: m B A: n, HKAB(n, m, B) A B: HKAB(n, m, A) SKID 3 Instantiation Abstraction A B: m B A: n, sig. B(n, m, A) A B: sig. A(n, m, B) ISO-9798 -3

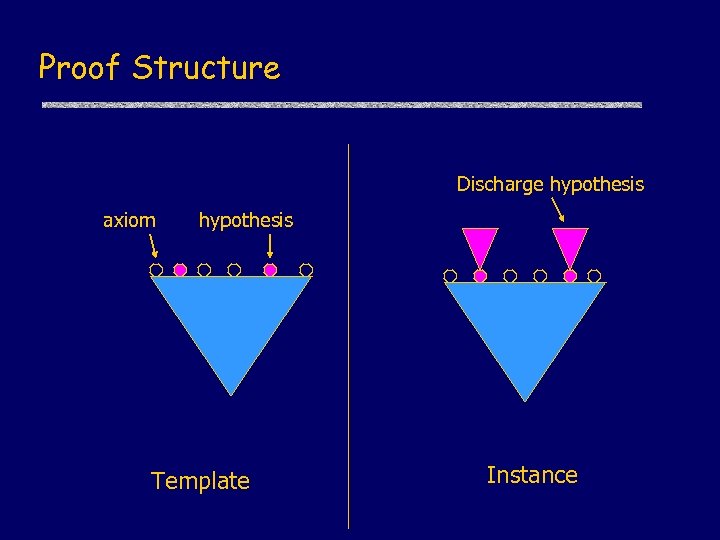Proof Structure Discharge hypothesis axiom hypothesis Template Instance

Sample projects using this method u. Key exchange • STS family, JFK, IKEv 2 • Diffie-Hellman -> MQV • GDOI [Meadows, Pavlovic] u. Work in progress • SSL verification • Wireless 802. 11 i

Symbolic vs Computational model u. Suppose |- [actions]X • If a protocol P satisfies invariants , then if X does actions, will be true u. Symbolic soundness • No idealized adversary acting against “perfect” cryptography can make fail u. Computational soundness • No probabilistic polytime adversary can make fail with nonnegligible probability

Conclusions u. Security Protocols • Subtle, critical, prone to error u. Analysis methods • Model checking – Practically useful; brute force is a good thing – Limitation: find errors in small configurations • Protocol derivation – Systematic development of certain classes of protocols • Proof methods – Time-consuming to use general logics – Special-purpose logics can be sound, useful • Cryptographic foundations – Scientific challenge; currently hot area

Collaborators on work described u. Former and current students • Vitaly Shmatikov, Ulrich Stern • Nancy Durgin, Anupam Datta, Ante Derek • Ajith Ramanathan, Changhua He, … u. Outside Stanford • Andre Scedrov (U Penn) • Patrick Lincoln (SRI) • Dusko Pavlovic (Kestrel)