Securing the Wireless World Sunday March 18 2018

Securing the Wireless World Sunday, March 18, 2018

Validation of Elliptic Curve Public Keys Adrian Antipa*, Dan Brown*, Alfred Menezes+, Rene Struik* and Scott Vanstone+* PKC 2003 Miami, Florida Jan 7, 2003 Presented by Dan Brown * Certicom Research + U. Waterloo Sunday, March 18, 2018

Outline • • • ECC and Public Key Validation Attacking ECIES, 1 -Pass ECDH, & ECMQV Inadequacy of Proof-of-Possession for ECPKV Improving Attack: Power Order Curves Modifying Attack for Compressed Points Countermeasures and Conclusions Securing the Wireless World

Elliptic Curve Cryptography in Standards (incl. Drafts & Proposals) • • ANSI X 9: 62, 63, 92, … IEEE: 1363 -2000, P 1363 a, P 1363. 2, P 802. 15. 3/4, … ISO: 14888 -3, 9496, 15496, 18033 -2, … FIPS: 186 -2, 2 XX, … NESSIE, IPA Cryptrec, … SECG: SEC 1, SEC 2, … IETF: PKIX, IPSec, SMIME, TLS, … SET, Media. Player, 5 C, WAP, … Securing the Wireless World

Elliptic Curves in Cryptography Usual elliptic curves (ANSI, SECG, FIPS): Ea, b(GF(p)): y 2=x 3+ax+b, Ea, b(GF(2 m)): y 2+xy=x 3+ax 2+b. • Group consists of: Pairs (x, y) satisfying curve equation, Point at infinity, “ 0”. • CRUCIAL FACT: b determinable from x, y, a. • Securing the Wireless World

Coefficient b as Function of x, y, a Securing the Wireless World

Elliptic Curve Group Law Usual formulae for EC group law: Do not use coefficient b, and Are the most efficient known. • Example: Over GF(p), compute 2(x, y) = (x’, y’): Set t = (3 x 2+a)/(2 y). Set x’ = t 2 -2 x. Set y’ = t(x-x’’)-y. • Securing the Wireless World

Elliptic Curve Domain Parameters • • Field size q. Coefficients a, b of E=Ea, b(GF(q)). Field representation (if q=2 m). Seed s (Optional). Base point G on curve E. Order n of G: should be prime. Cofactor h such that #E = hn. Usually h belongs to {1, 2, 4}. Securing the Wireless World

Elliptic Curve Public Key Validation (ECPKV) Input: Domain (E, n) and alleged point P. • Output: Valid or invalid. • Actions: Parse P and then output: Invalid if P = 0, Invalid if x or y invalid for GF(q), Invalid if equation for E fails for (x, y), Invalid if n. P is not 0, (*) Valid otherwise. * Note: Naïve n. P too slow (but tricks known). • Securing the Wireless World

ECPKV: Why and When? Why ECPKV: If not then: Private key stolen via following attacks. • When ECPKV: On any EC point to which an EC private key is applied: Static public key (ECDH, ECMQV), Ephemeral public key (ECDH, ECIES), Public keys for certification (ECDSA). • Scope: A variety of protocols are at risk. • Securing the Wireless World

Elliptic Curve Integrated Encryption Scheme (ECIES) - Encryption • • Input: Public key (static) Q in E, message M. Output: Ciphertext (R, S, A). Actions: Set R = r. G for random r in [1, n-1]. Set (s, a) = KDF(x( r. Q )). Set S = SYM(s, M) and A = MAC(a, S). Note: (R, r) ephemeral public-private key pair. Securing the Wireless World

ECIES - Decryption • • • Input: Private key q, ciphertext (R, S, A). Output: Invalid; or valid and message M. Actions: Set (s, a) = KDF( x( q. R )). Valid if A=MAC (a, S) else invalid. If valid, set M = SYM-1(s, S). Securing the Wireless World

Invalid Curve Attack on ECIES, Phase 1 Choose small integer n’. • Find curve E’ = Ea, b’ with n’ |#E’. • Find point R’ of order n’ on E’. • • Notation: Z’ indicates the adversary’s version of a variable Z. • Note: R’ generates “small subgroup” (cf. Lim and Lee, Crypto 97) of another group. Securing the Wireless World

Invalid Curve Attack, Phase 2 • • • Choose any message M’. Pick random q’ in [1, n’-1]. Compute (s’, a’) = KDF(x(q’R’)). Compute S’=SYM(s’, M’) and A’=MAC(a’, S). Send victim (R’, S’, A’). Securing the Wireless World

Victim Response to Phase 2 Victim receives (R’, S’, A’). • Victim decrypts with (s, a) = KDF(x(q. R’)). • If q=±q’ mod n’ then: x(q. R’) = x(q’R’), (s, a) = (s’, a’), A’ = MAC(a’, S’) = MAC(a, S’), M = SYM-1(s, S’) = SYM-1(s’, S’) = M’, “Valid” ciphertext decryption. • Securing the Wireless World

Invalid Curve Attack, Phase 3 • • • Observe reaction of victim. Determine validity or invalidity of (R’, S’, A’) Repeat Phase 2 until (R’, S’, A’) valid: If (R’, S’, A’) invalid, try another q’. Conclude q = ±q’ mod n’. This is partial information about victim’s private key q. Securing the Wireless World

Invalid Curve Attack, Phase 4 • • • Note: q 2=(±q’)2=(q’)2 mod n’. Repeat Phase 1 to 3 with various n’. Example: for small primes n’. Learn q 2 mod n’ for various n’. Chinese Remainder Theorem Combines info about q, Deduces q 2 exactly as integer. Find q by ordinary square root of q 2. Securing the Wireless World

Cost of Attack on ECIES • # of ciphertexts: (n 1+…+nk)/4 where ni is ith prime and n 1…nk > n 2. Bits in q Ciphertexts 192 1996 224 2548 256 3275 384 6735 521 11548 Securing the Wireless World

Attack on Ephemeral-Static ECDH • If responder (victim) uses shared key before initiator (adversary): Bits in q Ciphertexts 192 61(1) 224 68(1) 256 76(1) 384 105(1) 521 134(1) But, in practice, initiator (adversary) uses key first. • NOTE: Biehl, Meyer, Müller (Crypto 2000). • Securing the Wireless World

1 -Pass Menezes-Qu-Vanstone (MQV) Alice (Attacker) Bob (Victim) Static Key Ephemeral Key Securing the Wireless World

Attack on 1 -Pass ECMQV • • Same idea as ECIES but … Attacker needs invalid static key (certified). Attacker needs CA to certify invalid key. Attacker needs CA to skip ECPKV. Standards for PKI do not require (EC)PKV. Standards for PKI require POP. Does “proof-of-possession” stop attack? Securing the Wireless World

Proof of Possession via Certificate Requests Certificate request is a self-signed public key and identity information. • Signature “proves” possession of private key, which helps avoid certain other attacks. • ECDSA natural choice for EC public key. • Securing the Wireless World

Elliptic Curve Digital Signature Algorithm (ECDSA) - Verification • A pair (r, s) is a valid signature On message M, • For public key Q, • For EC domain (E, G, n) and • For hash function H, • If: r and s integers are in [1, n-1], and r=x((H(M)/s mod n)G+(r/s mod n)Q) mod n. Securing the Wireless World

Valid ECDSA Signature with Invalid Public Key • • • Input: Message M, valid EC domain (E, G, n), invalid public key info Q’ and n’. Output: Valid signature (r, s) on M in domain (E, G, n) under invalid public key Q’. Actions: Choose s in [1, n-1] and a in [1, n’-1]. Set r = x((H(M)/s mod n) G + a. Q’) mod n. If not a=(r/s mod n) mod n’ try again. Securing the Wireless World

Invalid Curve Attack on ECMQV • • • Choose invalid static public keys of orders n 1, n 2, …, nk. Generate ECDSA certificate requests. Get invalid static keys certified by lazy CA. Send invalid static and ephemeral keys to victim. Learn victim’s (static) private key. Securing the Wireless World

Special Curves for Accelerating Attack • • Pohlig-Hellman approach works if #E’ is divisible by powers of small primes. Example: NIST field GF(2521 -1). Let E’=E-3, 0: y 2=x 3 -3 x (supersingular). Then #E’ = 2521. Attack uses 521 ciphertexts (< 11548). Problem 1: Find #E’(GF(2 m))=2 m. Problem 2: Find #E’(GF(p))=2 m (or 2 md). Securing the Wireless World

Elliptic Curve Point Compression Compressed point (x, z) where z=0 or z=1. • Decompression solves quadratic for y. • Bit z determines which y, if any, to use for the decompressed point (x, y). • Securing the Wireless World

Invalid Compressed Points • • • Fixing x leaves 0, 1, or 2 solutions for y. Half of x have 0 solutions for y. Element x invalid if y has 0 solutions. Compressed point (x’, z) invalid if x’ invalid. Reject invalid compressed points. Can an invalid compressed point be “used”? Securing the Wireless World

Invalid Decompression in GF(p) Fact: If p=3 mod 4, then y 2=w can be solved as y=f(w)=w(p+1)/4 mod p. • Proof: y 2=w(p+1)/2=wp-(p-1)/2=w(w/p) mod p, where (w/p) is the Legendre symbol, which is 1 (or 0) if w has a square root and – 1 if not. • Note: If x invalid, an invalid compressed point (x, z) can be decompressed to (x, y) where y=(x 3+ax+b)(p+1)/4. • Securing the Wireless World

1 -Time Setup: Finding Low Order Invalid Compressed Points • Fact: If x invalid then y 2=-(x 3+ax+b) mod p, since if w has no square root then f(w)2=-w. • Output: Invalid x with (x, y) of low order m Actions: Find division polynomial in x and b’. Substitute b’ = -2(x 3+ax+b). Find invalid root x of subbed poly. Problem 3: Setup cost as Schoof for #E? • • • Securing the Wireless World

Order 11 Invalid Compressed Point • Consider the octet string: 02 2 f 8 c 8 c 8 a 7 c b 1 1 c 06 aa a 3 4 b 23 4 f 7 d 88 cd b 9 9 f d 7 66 4 a 00 a 4 d 7. Parses under FIPS 186 -2 EC domain P-192 (secp 192 r 1) to invalid compressed point. • Non-validated decompression gives order 11. • Found with Maple, by solving degree 60 poly. • Securing the Wireless World

Countermeasures Best: Validate EC public keys: Ephemeral and static, When verifying and decrypting, In key agreement. • Special EC arithmetic: Eg: Koblitz curves (used for efficiency). “Frobenius” map is f: (x, y) -> (x 2, y 2). Invalid curves: f moves off curve. Invalid curve attack seems to fail. • Securing the Wireless World

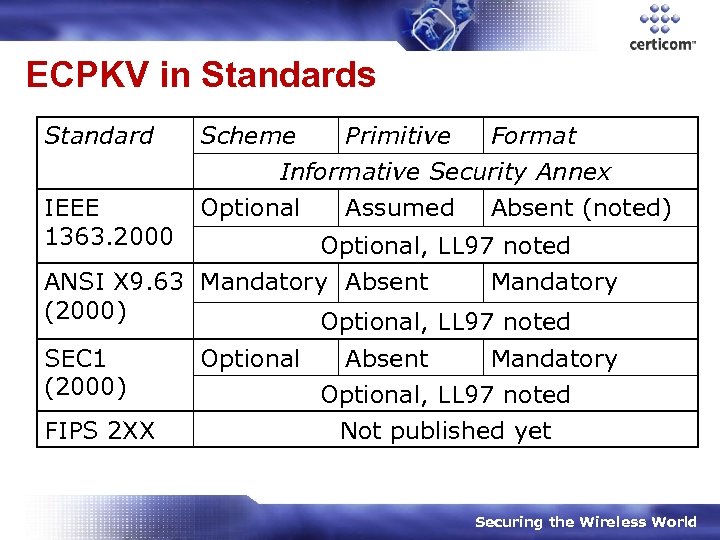ECPKV in Standards Standard IEEE 1363. 2000 Scheme Primitive Format Informative Security Annex Optional Assumed Absent (noted) Optional, LL 97 noted ANSI X 9. 63 Mandatory Absent Mandatory (2000) Optional, LL 97 noted SEC 1 (2000) FIPS 2 XX Optional Absent Mandatory Optional, LL 97 noted Not published yet Securing the Wireless World

Conclusions Elliptic curve private keys risk being compromised if applied to invalid EC points. • Standards have not provided adequate warning about this attack. • Securing the Wireless World

References I. Biehl, B. Meyer, and V. Müller, “Differential fault analysis on elliptic curve cryptosystems”, Advances in Cryptology – CRYPTO 2000, Lecture Notes in Computer Science 1880, pp. 131 -146. • C. Lim and P. Lee, “A key recovery attack on discrete log-based schemes using a prime order subgroup”, Advances in Cryptology CRYPTO 97, Lecture Notes in Computer Science 1294, pp. 249 -263. • Securing the Wireless World