a0bbc186f78740ec535ee38e1a844065.ppt
- Количество слайдов: 46

Secure Electronic Commerce Prof. Amir Herzberg Seminar 89 -957, Wedn. 6 -8 pm CS Dept. , Bar Ilan University סמינר: אבטחת סחר אלקטרוני Lecture 1: Overview of security & crypto Network Security 1

Administration r Seminar for graduate & undergrad students r Related courses: m Intro to communication networks 89 -350 (parallel Ok) m Intro to Cryptography (89 -656, fall term) m This term: Crypto applied to security (89 -956): requires intro first m I’ll try to cover the most relevant stuff in the first 2 -3 lectures r Requirements m Deliver seminar for one topic m Few in pairs m Attend and understand most classes • Missing 2 is Ok; if more: justify all r Reception: Wedn. 12 -2, room 324. Network Security 2

Goals of this seminar r Understand secure e-commerce r Expose to recent, active research area m Possibilities of new research r Experience in research work – reading, presenting Network Security 3

Subjects r Payments m Micropayments m Aggregated (micro)payments m Anonymous payments (digital cash) r Trust and credential management m Overview including Key. Note, SPKI m Understanding Trust Management Systems m Credentials / Certificate Chain Discovery r Others? You can propose… Network Security 4

What to do next? r Pick subject: m See site for subjects, papers and dates • Two pairs, few singles m m m Site: link from my homepage, http: //amir. herzberg. name/ Inform me of your choices (2 please) by e-mail Only if you’re going to deliver… `a honor commitment` r Read paper(s) carefully, prepare lecture, handouts m See related papers in http: //citeseer. org m Ask to change if you prefer another paper/topic m Use English or Hebrew, foils or PC (but write well!) m Give me a copy r We next give overview of crypto & security m You can leave if not interested (e. g. know already) Network Security 5

Security and Cryptography Overview Goals: r understand principles of network security: m cryptography and its many uses beyond “confidentiality” m authentication m message integrity m key distribution r security in practice: m firewalls m security in application, transport, network, link layers Network Security 6

What is network security? Confidentiality: only sender, intended receiver should “understand” message contents m sender encrypts message m receiver decrypts message m Privacy: hide `who is doing what with whom` Authentication: sender, receiver want to confirm identity of each other Message Integrity: sender, receiver want to ensure message not altered (in transit, or afterwards) without detection Access and Availability: services must be accessible and available to users Network Security 7
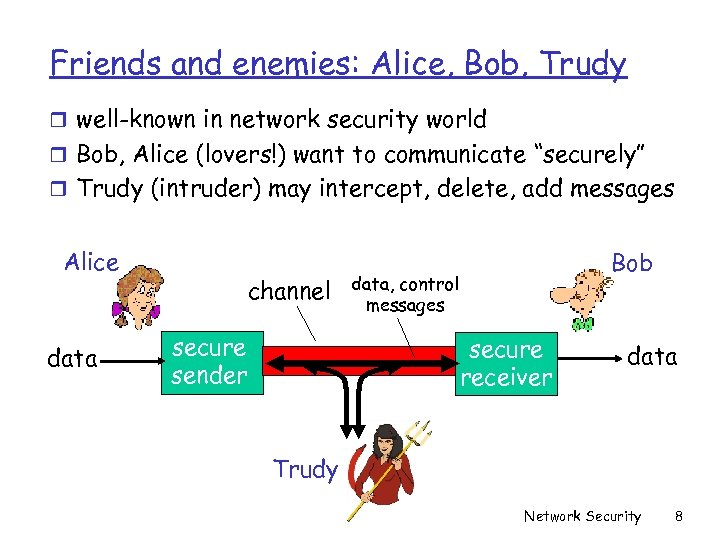
Friends and enemies: Alice, Bob, Trudy r well-known in network security world r Bob, Alice (lovers!) want to communicate “securely” r Trudy (intruder) may intercept, delete, add messages Alice data channel secure sender Bob data, control messages secure receiver data Trudy Network Security 8

There are bad guys (and girls) out there! Q: What can a “bad guy” do? A: a lot! m eavesdrop: intercept messages m actively insert messages into connection m impersonation: can fake (spoof) source address in packet (or any field in packet) m hijacking: “take over” ongoing connection by removing sender or receiver, inserting himself in place m denial of service: prevent service from being used by others (e. g. , by overloading resources) Cryptography can help …… Network Security 9
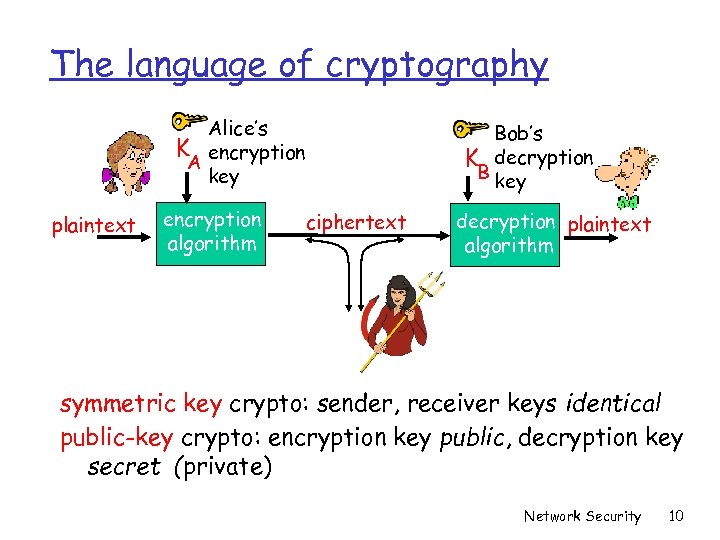
The language of cryptography Alice’s K encryption A key plaintext encryption algorithm Bob’s K decryption B key ciphertext decryption plaintext algorithm symmetric key crypto: sender, receiver keys identical public-key crypto: encryption key public, decryption key secret (private) Network Security 10

Symmetric key cryptography KA-B plaintext message, m encryption ciphertext algorithm K (m) A-B decryption plaintext algorithm m=K A-B ( KA-B(m) ) symmetric key crypto: Bob and Alice share know same (symmetric) key: K A-B r e. g. , key is knowing substitution pattern in mono alphabetic substitution cipher r Q: how do Bob and Alice agree on key value? Network Security 11

Public Key Cryptography symmetric key crypto r requires sender, receiver know shared secret key r Q: how to agree on key in first place (particularly if never “met”)? public key cryptography r radically different approach [Diffie. Hellman 76, RSA 78] r sender, receiver do not share secret key r public encryption key known to all r private decryption key known only to receiver Network Security 12
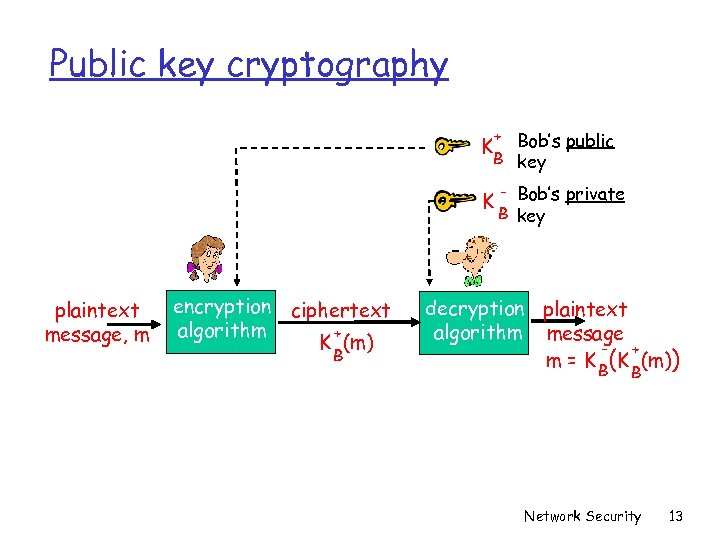
Public key cryptography + Bob’s public B key K K plaintext message, m encryption ciphertext algorithm + K (m) B - Bob’s private B key decryption plaintext algorithm message + m = K B(K (m)) B Network Security 13

Public key encryption algorithms Requirements: 1 2 . . + need K B( ) and K - ( ) such that B - + K (K (m)) = m B B + given public key KB , it should be impossible to compute private key K B RSA: Rivest, Shamir, Adelman algorithm Network Security 14

RSA: Choosing keys 1. Choose two large prime numbers p, q. (e. g. , 1024 bits each) 2. Compute n = pq, z = (p-1)(q-1) 3. Choose e (with e<n) that has no common factors with z. (e, z are “relatively prime”). 4. Find d such that ed-1 is exactly divisible by z. (in other words: ed mod z = 1 ). 5. Public key is (n, e). Private key is (n, d). + KB - KB Network Security 15

RSA: Encryption, decryption 0. Given (n, e) and (n, d) as computed above 1. To encrypt bit pattern, m, compute e mod n (i. e. , remainder when m e is divided by n) c=m 2. To decrypt received bit pattern, c, compute d m = c d mod n (i. e. , remainder when c is divided by n) Magic d m = (m e mod n) mod n happens! c Network Security 16

RSA example: Bob chooses p=5, q=7. Then n=35, z=24. e=5 (so e, z relatively prime). d=29 (so ed-1 exactly divisible by z. encrypt: decrypt: letter m me l 12 1524832 c 17 d c 48196857210675091411825223071697 c = me mod n 17 m = cd mod n letter 12 l Network Security 17

RSA: m = (m e mod n) Why is that d mod n Useful number theory result: If p, q prime and n = pq, then: y y mod (p-1)(q-1) x mod n = x mod n e (m mod n) d mod n = med mod n = m ed mod (p-1)(q-1) mod n (using number theory result above) 1 = m mod n (since we chose ed to be divisible by (p-1)(q-1) with remainder 1 ) = m Network Security 18

RSA: another important property The following property will be very useful later: - + B B K (K (m)) + = m = K (K (m)) B B use public key first, followed by private key use private key first, followed by public key Result is the same! Network Security 19

Roadmap. 1 What is network security? . 2 Principles of cryptography. 3 Authentication and integrity mechanisms. 4 Digital Signatures. 5 Key Distribution and certification. 6 Attacks and counter measures. 7 Access control: firewalls. 8 Security in many layers Network Security 20
Example: `paper, stone, scissors` r Popular kids game r Kid’s implementation: m `Simultaneous` exposure m Cheating common… r Physical implementation: m Write choice on card m Cards placed `face down` m Choices fixed but secret m Cards turned r How to do over network? Bob Alice Network Security 21
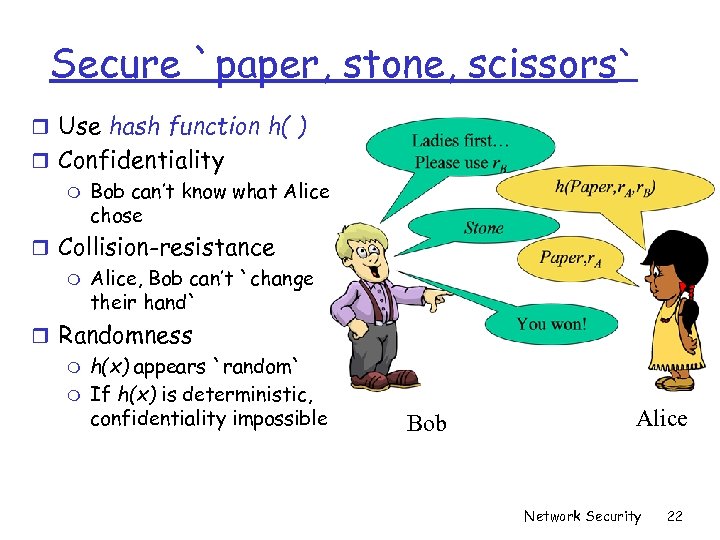
Secure `paper, stone, scissors` r Use hash function h( ) r Confidentiality m Bob can’t know what Alice chose r Collision-resistance m Alice, Bob can’t `change their hand` r Randomness m h(x) appears `random` m If h(x) is deterministic, confidentiality impossible Bob Alice Network Security 22

Crypto-Hash Functions - `Wish List` r Compression m Unbounded/Long input m Short (finite) output r Confidentiality m Can’t find x from h(x) r Collision-resistance m `Strong`: can’t find x, x’ s. t. h(x)=h(x’) m `Weak`: given x, can’t find x’≠x s. t. h(x)=h(x’) r Randomness: uniform output distribution Network Security 23
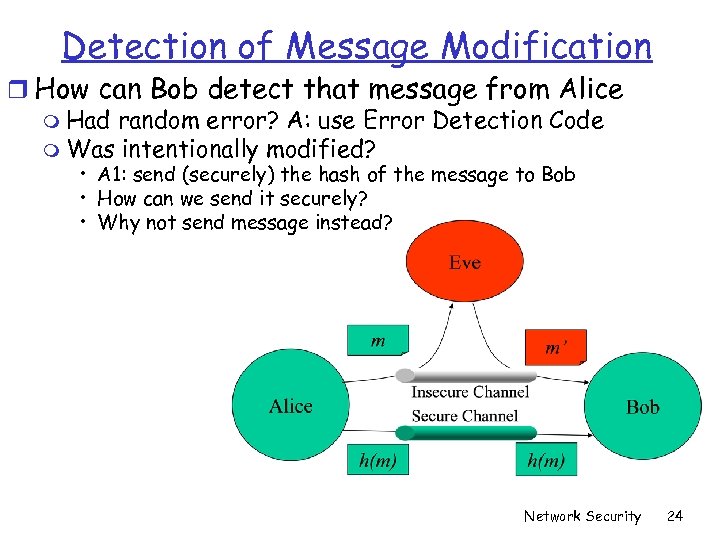
Detection of Message Modification r How can Bob detect that message from Alice m Had random error? A: use Error Detection Code m Was intentionally modified? • A 1: send (securely) the hash of the message to Bob • How can we send it securely? • Why not send message instead? Network Security 24
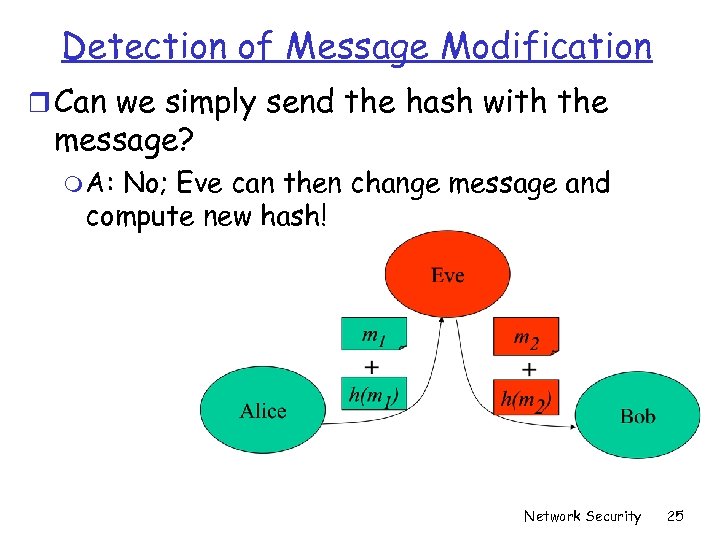
Detection of Message Modification r Can we simply send the hash with the message? m A: No; Eve can then change message and compute new hash! Network Security 25
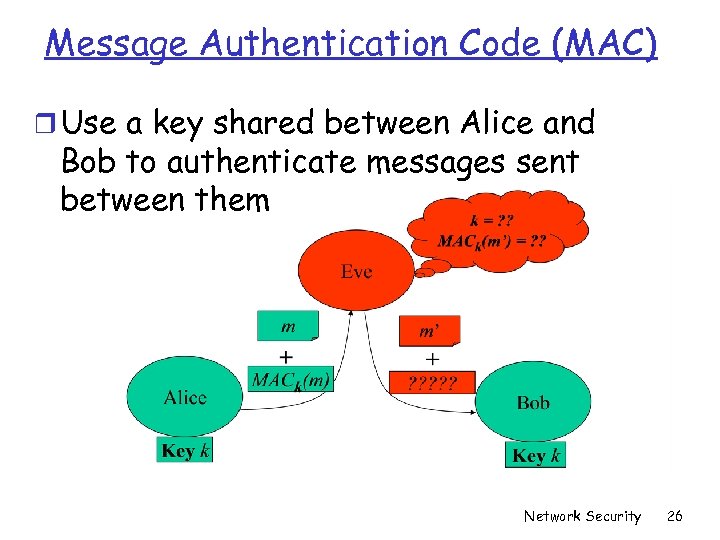
Message Authentication Code (MAC) r Use a key shared between Alice and Bob to authenticate messages sent between them Network Security 26
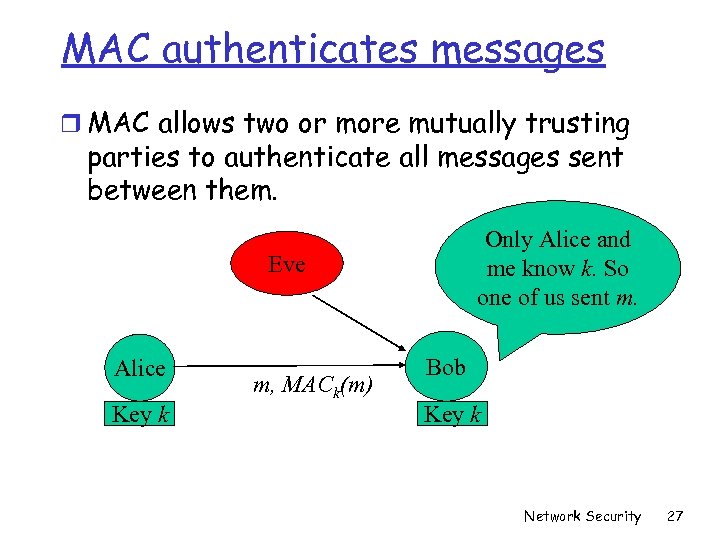
MAC authenticates messages r MAC allows two or more mutually trusting parties to authenticate all messages sent between them. Only Alice and me know k. So one of us sent m. Eve Alice Key k m, MACk(m) Bob Key k Network Security 27
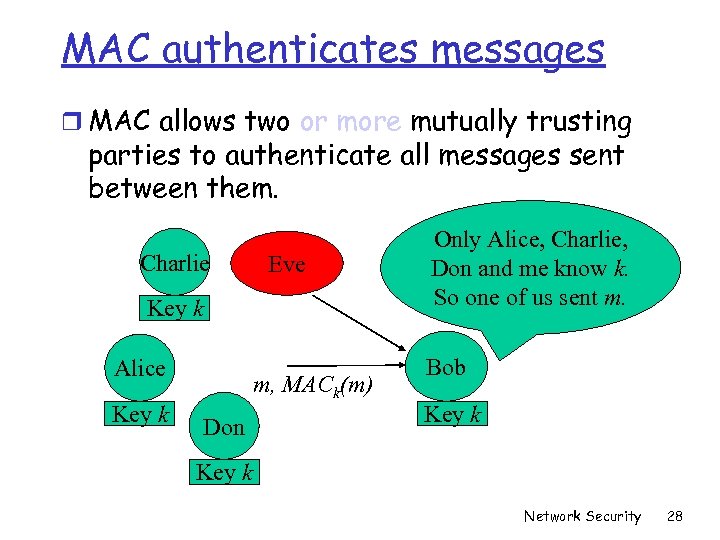
MAC authenticates messages r MAC allows two or more mutually trusting parties to authenticate all messages sent between them. Charlie Eve Key k Alice Key k m, MACk(m) Don Only Alice, Charlie, Don and me know k. So one of us sent m. Bob Key k Network Security 28

MAC Use Secret Key r Random or pseudo-random r Do not reveal to adversary r Do not use for anything except MAC m. E. g. use different key for encryption Network Security 29

Limitations of MAC r MACk(m) may expose information about m! m Example: Let MAC be any secure MAC. Define MAC’k(m)=LSb(m)||MACk(m), where LSb is least significant bit. r MAC only shows a key-holder computed it r Could be any key holder (e. g. recipient)… Specify sender, recipient in message r Could be re-transmission / replay… Add time/counter/random challenge to identify Network Security 30
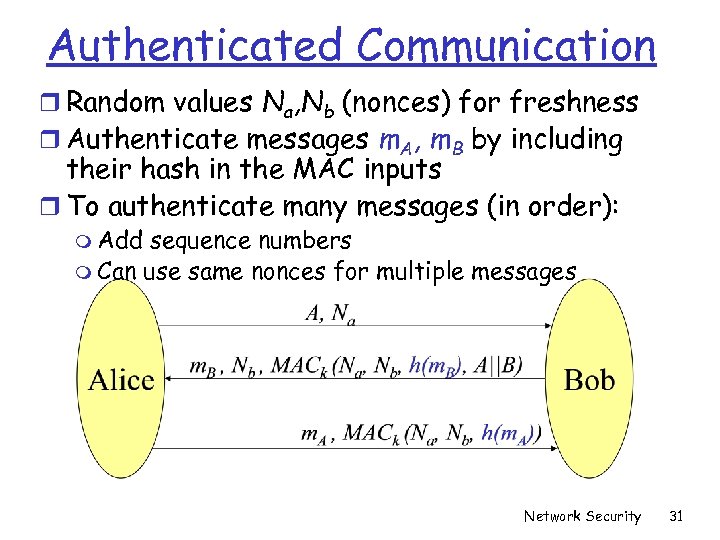
Authenticated Communication r Random values Na, Nb (nonces) for freshness r Authenticate messages m. A, m. B by including their hash in the MAC inputs r To authenticate many messages (in order): m Add sequence numbers m Can use same nonces for multiple messages Network Security 31

Non-repudiation r Non-repudiation: proof of authenticity that cannot be disputed by `signer` m m Long-lived Validation by multiple, arbitrary parties r Not ensured by MAC – key known to both! r Applications: m Contract/document//payment signing m Time-stamping of documents m Guaranteed/Certified Messaging Services r Main tool: digital signatures and certificates Network Security 32
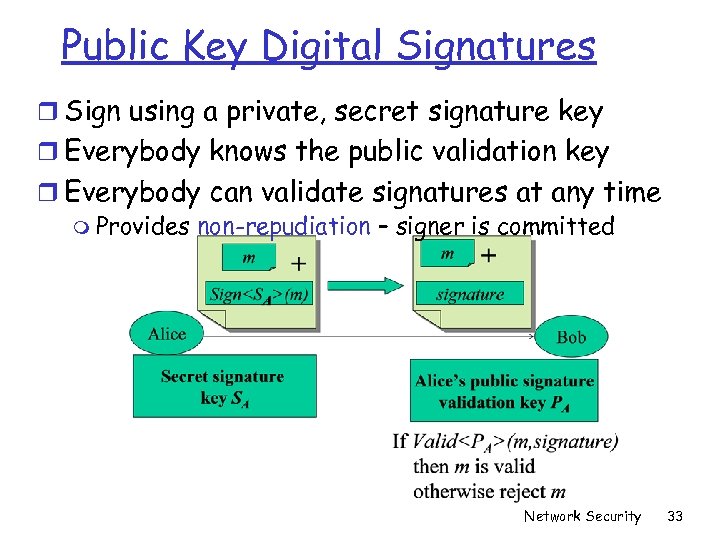
Public Key Digital Signatures r Sign using a private, secret signature key r Everybody knows the public validation key r Everybody can validate signatures at any time m Provides non-repudiation – signer is committed Network Security 33

Metaphor to Public Key Signature: Cylinder Seal (ancient Iran) r Public key: impression of seal r Private key: cylinder seal r Hard to create impression without seal r Hard to change clay tablet with impression r Hard to create the seal from the impression r Clay tablets (w/ impressions) last long time Network Security 34
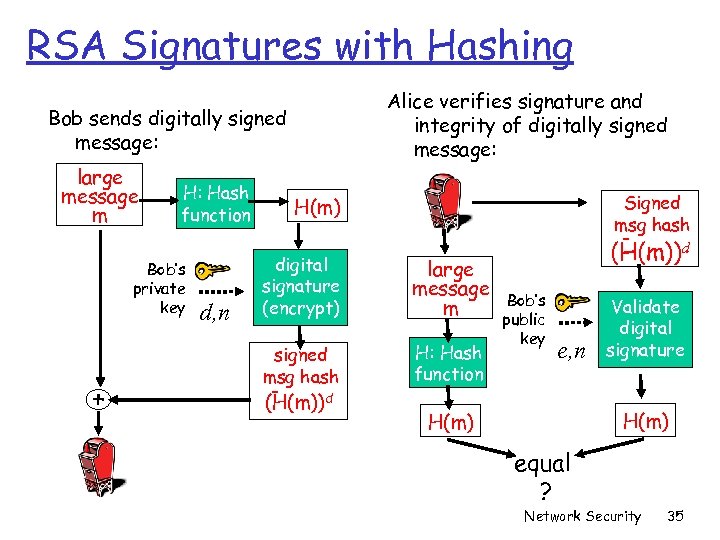
RSA Signatures with Hashing Alice verifies signature and integrity of digitally signed message: Bob sends digitally signed message: large message m H: Hash function Bob’s private key + d, n Signed msg hash H(m) - digital signature (encrypt) large message m signed msg hash H: Hash function (H(m))d Bob’s public key e, n Validate digital signature H(m) equal ? Network Security 35

Problem: validation of public key r How does Alice obtain Bob’s public key… m To encrypt messages to Bob m To validate signatures by Bob r If Eve can cause Bob to use Eve’s key thinking it is Alice’s key… m Eve can decrypt messages sent to Alice m Eve can pretend to sign for documents as Alice r Solution: certificate: signed public key Network Security 36
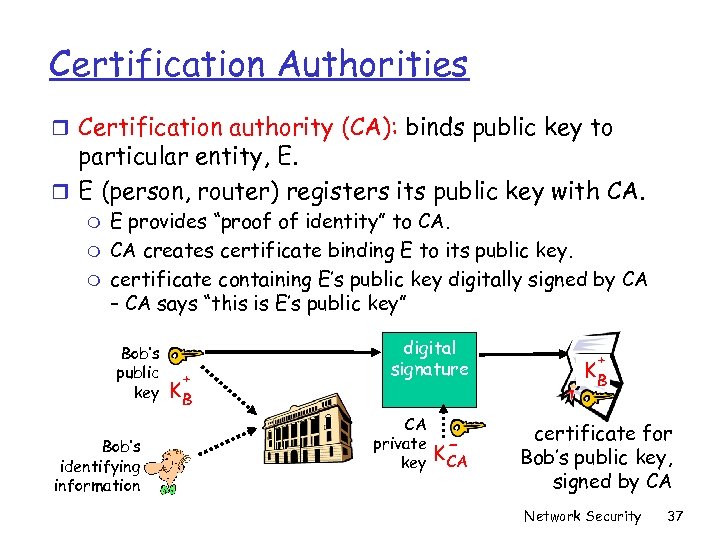
Certification Authorities r Certification authority (CA): binds public key to particular entity, E. r E (person, router) registers its public key with CA. m m m E provides “proof of identity” to CA. CA creates certificate binding E to its public key. certificate containing E’s public key digitally signed by CA – CA says “this is E’s public key” Bob’s public key Bob’s identifying information + KB digital signature CA private key K- CA + KB certificate for Bob’s public key, signed by CA Network Security 37
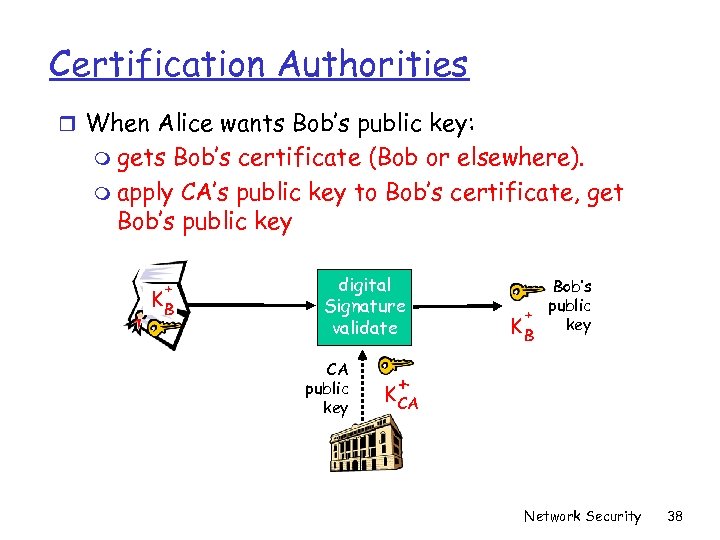
Certification Authorities r When Alice wants Bob’s public key: m gets Bob’s certificate (Bob or elsewhere). m apply CA’s public key to Bob’s certificate, get Bob’s public key + KB digital Signature validate CA public key Bob’s public + key KB + K CA Network Security 38

A certificate contains: r Serial number (unique to issuer) r info about certificate owner, including algorithm and key value itself (not shown) r info about certificate issuer r valid dates r digital signature by issuer Network Security 39

Time-Stamping of Signatures, etc. r Goal: non-repudiated proof of document creation date m Proof doc/signature existed at/before date m Signature existed before public key was revoked it is valid r Timestamp signed by Time-stamping Authority r Hash document to protect confidentiality Author h(doc) (paper, invention) Relying Party h(doc, sign), certificate(PK) Time-Stamping Authority (TSA) Network Security 40

Non-Repudiated Delivery Services Delivery Authority Origin r Non-Repudiation of Origin (NRO) m m r Destination proves that it received the message, originated by the origin, at particular time. Signature of Delivery Authority and/or Origin + Time. Stamping Auth. Non-Repudiation of Submission (NRS) m r Destination Origin proves it submitted the message, to the destination, at particular time by signature of Delivery Authority Non-Repudiation of Receipt (NRR) m Origin proves that the destination received the message, at particular time by signature of destination + TSA Network Security 41

SSL / TLS in a Nutshell r SSL provides a `secure TCP tunnel from client to server`: m Confidentiality m Authentication of server, optionally also of client m Message and connection integrity r SSL: Secure Socket Layer m Since SSL (& TLS) operate on top of `standard` Sockets API r TLS: Transport Layer Security m Since TLS (& SSL) secure TCP (the transport layer) m IETF standard version of SSL m When we describe common aspects we usually say just SSL Network Security 42
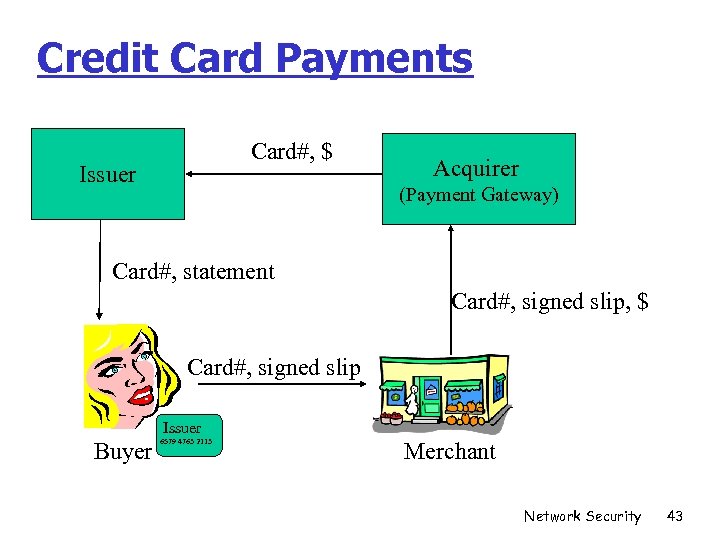
Credit Card Payments Card#, $ Issuer Acquirer (Payment Gateway) Card#, statement Card#, signed slip, $ Card#, signed slip Issuer Buyer 6579 4763 2113 Merchant Network Security 43
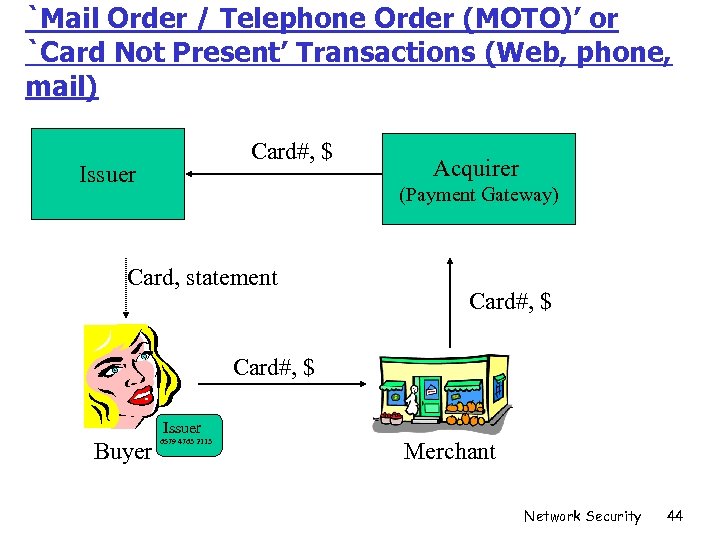
`Mail Order / Telephone Order (MOTO)’ or `Card Not Present’ Transactions (Web, phone, mail) Card#, $ Issuer Acquirer (Payment Gateway) Card, statement Card#, $ Issuer Buyer 6579 4763 2113 Merchant Network Security 44
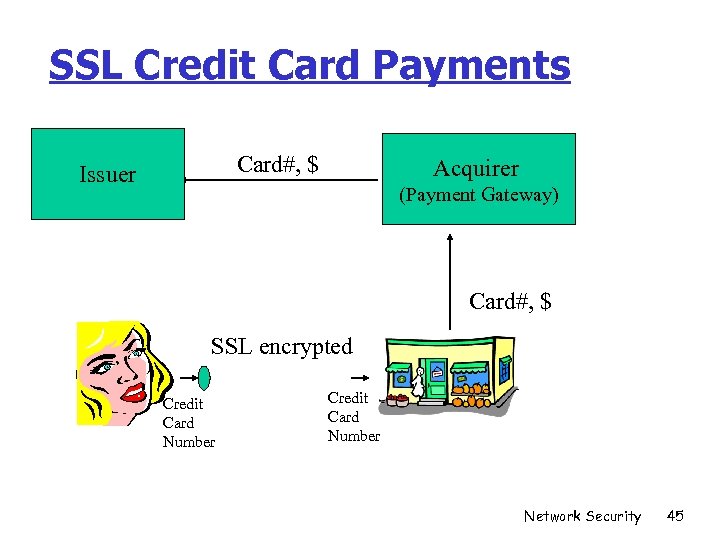
SSL Credit Card Payments Card#, $ Issuer Acquirer (Payment Gateway) Card#, $ SSL encrypted Credit Card Number Network Security 45

SSL Based Credit Card Payments r Use SSL to securely transfer credit card numbers r Trivial deployment (merchant decision). r No client software required (SSL is in browser). r Built on top of the existing credit card infrastructure. r By far, the most widely used payment method. But, due to several security problems… ÜVery high dispute rates (esp. for online services) ÜVery expensive for banks and merchants Network Security 46
a0bbc186f78740ec535ee38e1a844065.ppt