Section 6 5 Trees Trees Two Examples

Section 6. 5 Trees

Trees Two Examples Definition Examples 6. 5 Trees 2

3 Topics 1. Minimal Cost Spanning Trees 2. Counting Trees 3. Searching Trees Animations 6. 5 Trees 3

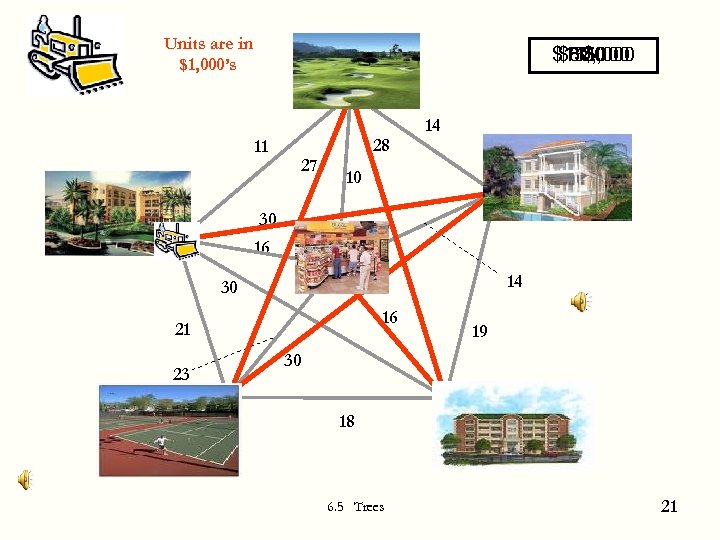
Minimal Cost Spanning Tree Example: A planned community Build a road system to begin for a 1000 -acre planned community. It will include a convenience store, golf course, tennis courts, and three condo units The developer has two goals 1. 2. 6. 5 Trees 4

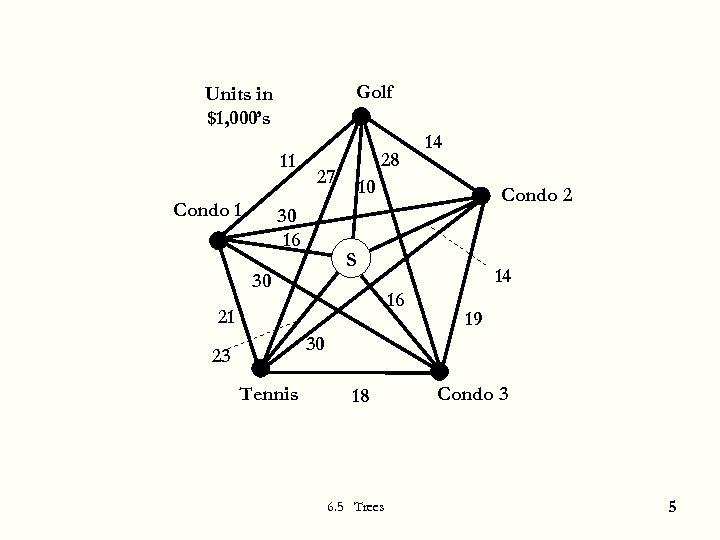Golf Units in $1, 000’s 11 Condo 1 28 27 30 16 14 10 Condo 2 S 30 14 16 21 19 30 23 Tennis 18 6. 5 Trees Condo 3 5

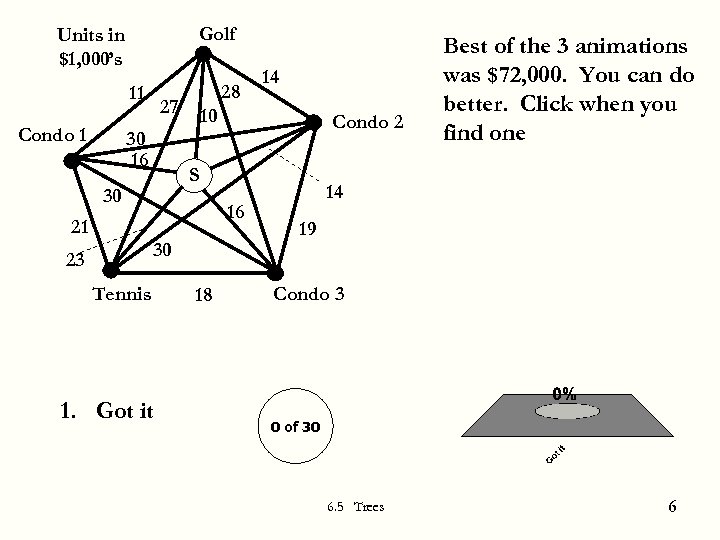Golf Units in $1, 000’s 11 Condo 1 28 27 30 16 10 Condo 2 S 30 16 21 30 23 14 Tennis 1. Got it 18 Best of the 3 animations was $72, 000. You can do better. Click when you find one 14 19 Condo 3 0 of 30 6. 5 Trees 6

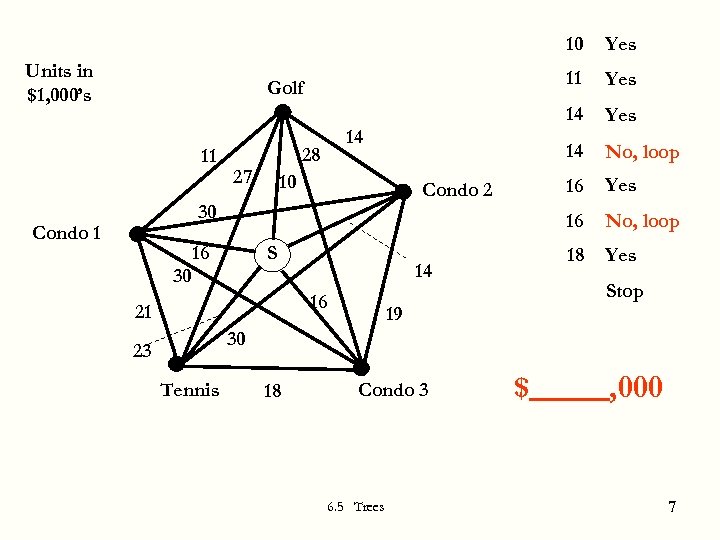10 11 11 27 10 16 30 Condo 1 16 S 14 30 16 21 Yes No, loop 18 Condo 2 No, loop 16 28 14 Yes 14 Golf Yes 14 Units in $1, 000’s Yes Stop 19 30 23 Tennis 18 Condo 3 6. 5 Trees $ , 000 7

Summarize the Algorithm 1. 2. 3. Resulting set of edges is called a minimal cost spanning tree Joseph Kruskal 6. 5 Trees 8

Understanding the terms “Minimal cost” = “Spanning” = No isolated vertices “Tree” = A graph with no loops 6. 5 Trees Obvious 9

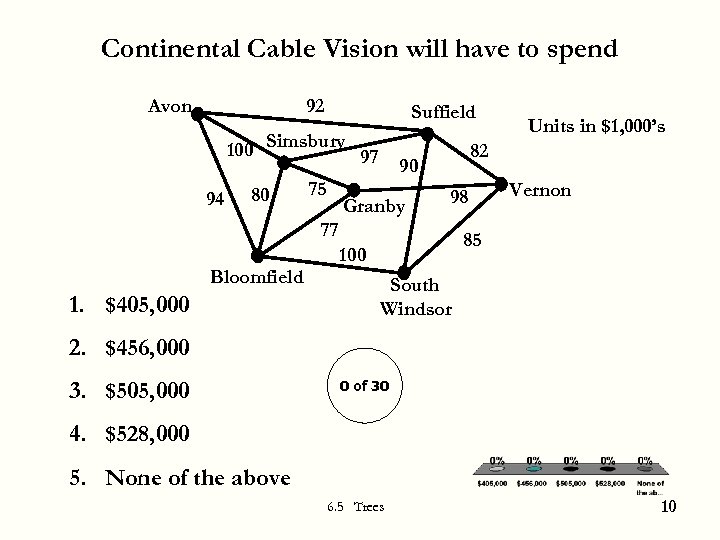Continental Cable Vision will have to spend 92 Avon Suffield 100 Simsbury 97 94 80 75 82 90 Granby 98 77 Bloomfield 1. $405, 000 Units in $1, 000’s Vernon 85 100 South Windsor 2. $456, 000 3. $505, 000 0 of 30 4. $528, 000 5. None of the above 6. 5 Trees 10

2. Counting Two teams, A and B, play a “best-of 5” game series. For example, here are some ways that A could win: In how many different ways can A win the series? 6. 5 Trees 11

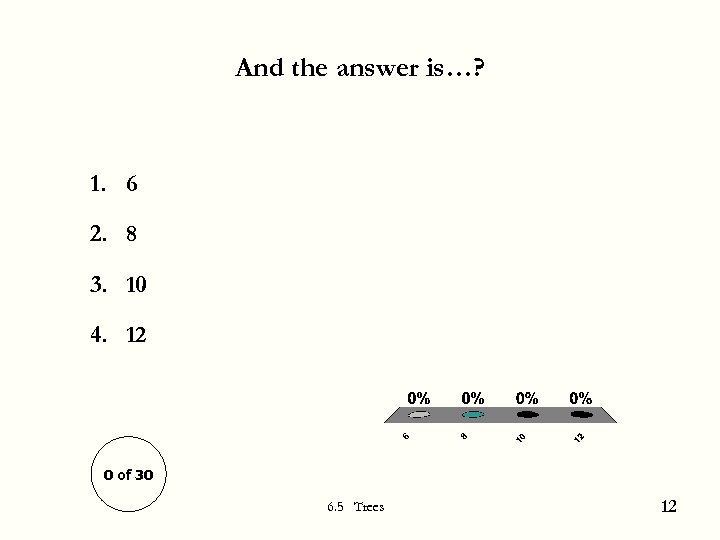And the answer is…? 1. 6 2. 8 3. 10 4. 12 0 of 30 6. 5 Trees 12

A “Tree” Solution 6. 5 Trees 13

“Red Sox vs. Yanks” The Red Sox play the Yanks in an unusual 4 -game series. If the visiting team (in this case the beloved Red Sox) wins two games, they win the series. The home team must win three games to win the series For example: In how many different ways can the series be played? 6. 5 Trees 14

And the answer is…? 1. 4 ways 2. 6 ways 3. 8 ways 4. 10 ways 6. 5 Trees 15

6. 5 Trees 16

A red chip, a white chip, and a blue chip are placed in a container. A person blindly picks one chip, notes its color, and then replaces it in the container. The person then chooses a second chip from the container and notes its color. Use a tree to determine the number of ways in which exactly one of the two chips drawn is the blue chip 1. 2 2. 3 3. 4 4. 5 6. 5 Trees 17

3. Searching You secretly choose an integer from 1 -100. I claim that I can find your number after I ask you X “yes/no” questions. What is X? 1. 7 -10 2. 11 -15 3. 16 -20 4. More than 20 6. 5 Trees 18

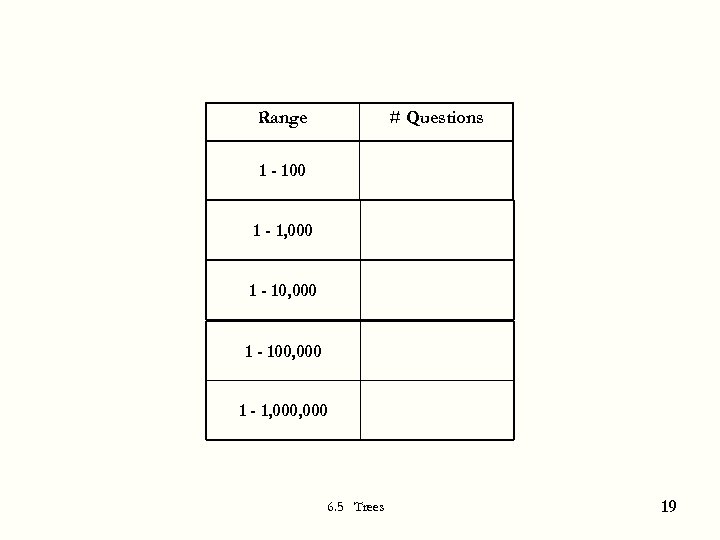Range # Questions 1 - 100 1 - 1, 000 1 - 100, 000 1 - 1, 000 6. 5 Trees 19

End of 6. 5 Trees

Units are in $1, 000’s $131, 000 $115, 000 $87, 000 $57, 000 $30, 000 $0 14 11 27 28 10 30 16 14 30 16 21 23 19 30 18 6. 5 Trees 21

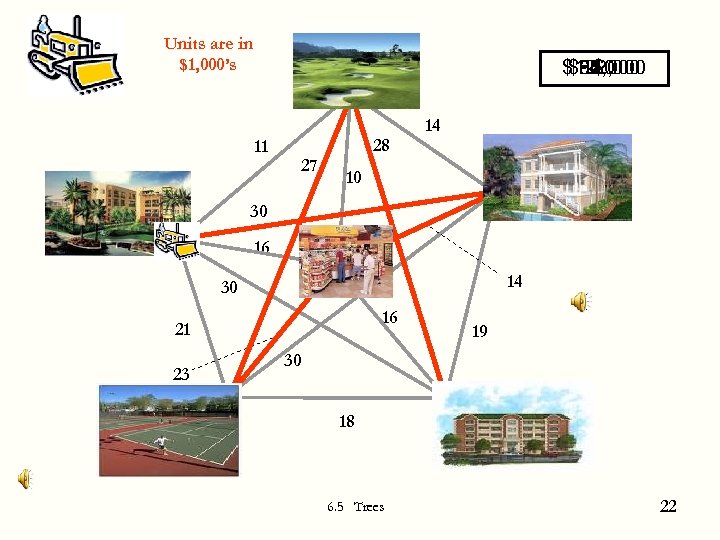Units are in $1, 000’s $122, 000 $94, 000 $67, 000 $53, 000 $30, 000 $0 14 11 27 28 10 30 16 14 30 16 21 23 19 30 18 6. 5 Trees 22

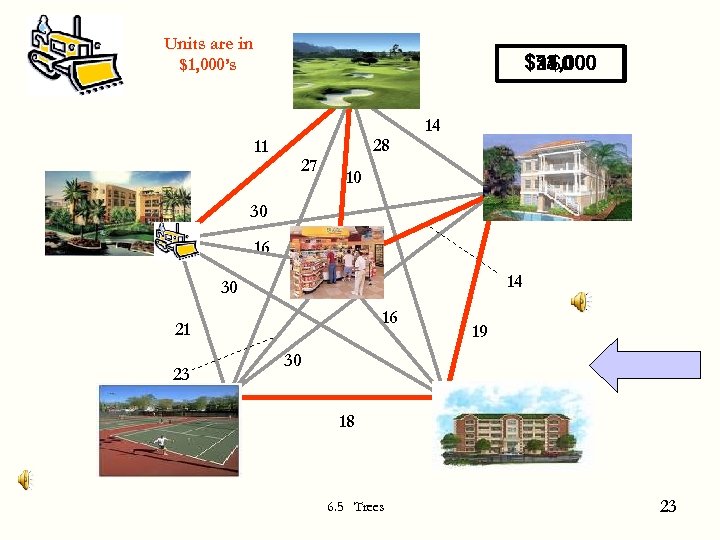Units are in $1, 000’s $72, 000 $54, 000 $11, 000 $35, 000 $0 $21, 000 14 11 27 28 10 30 16 14 30 16 21 23 19 30 18 6. 5 Trees 23

Family Trees 6. 5 Trees 24

Zork 6. 5 Trees 25

Minimal Cost Spanning Trees Joseph B. Kruskal 1928 - 6. 5 Trees 26

Meta - Material 6. 5 Trees

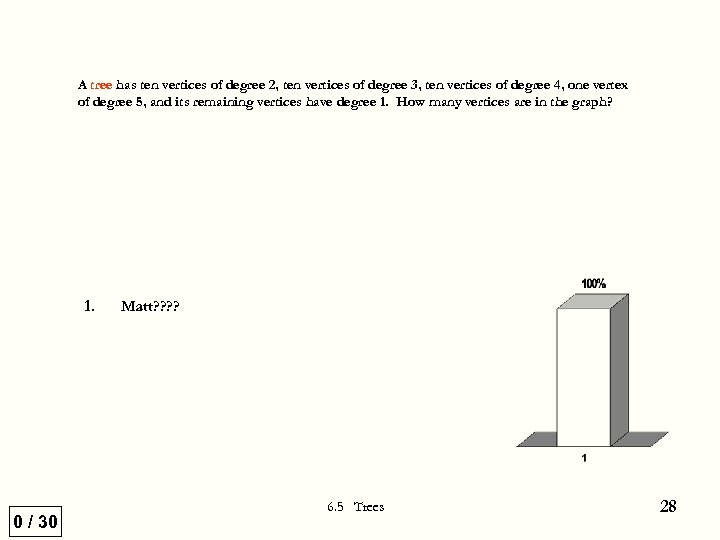A tree has ten vertices of degree 2, ten vertices of degree 3, ten vertices of degree 4, one vertex of degree 5, and its remaining vertices have degree 1. How many vertices are in the graph? 1. 0 / 30 Matt? ? 6. 5 Trees 28

Cheapest Link • Like NN start with two closest vertices, but keep on selecting pairs of vertices with the shortest distance between them. Not just the ones adjacent to the already selected pairs. • • Restrictions: don’t complete a circuit until all vertices are included A link may not be added if it results in more than two edges coming from the same vertex 6. 5 Trees 29

Nearest Insertion • Start once again with two closest vertices • Then make a circuit using those two and a third vertex, namely the one that is nearer to either one of the original two vertices Now include the unused vertex closest to any of the three. • 6. 5 Trees 30

Bonus questions • • Jack and Jill were at a party with three other married couples. As people were introduced a good deal of handshaking took place. No one shook hands with his or her spouse No none shook hands with herself or himself No one shook hands with anyone more than once. When leaving the party, Jill asked the other seven people how many hands they had shaken aand received 7 different answers. How many hands did Jill shake at the party? How many handshakes for Jack? 6. 5 Trees 31

Ex. 3 Oil Pipeline A pipeline is to be constructed to take oil across the northern part of Canada Find the minimum cost to ship the oil between connecting points 6. 5 Trees 32

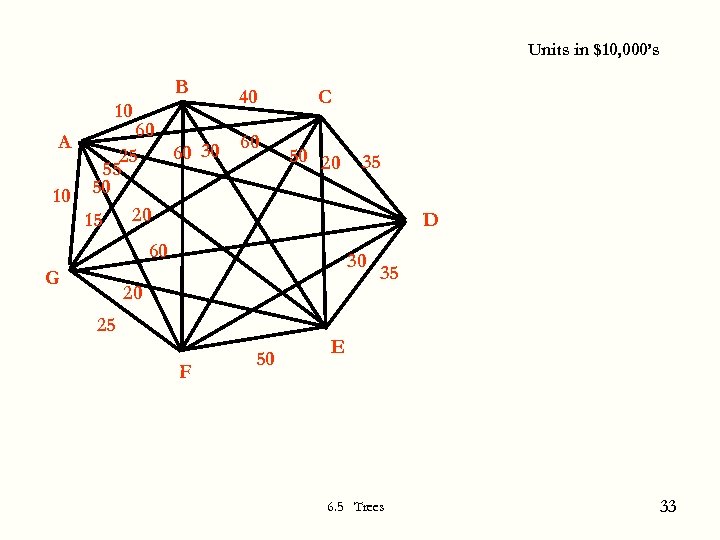Units in $10, 000’s B 10 60 60 30 25 55 10 50 15 20 A 40 60 C 50 20 D 60 G 35 30 20 35 25 F 50 E 6. 5 Trees 33

And, the answer is …. . (Choose the closest answer) 1. 2. $55, 000 3. $59, 000 4. $69, 000 5. 0 / 30 $49, 000 $73, 000 6. 5 Trees 34

Test question? If there are N locations (vertices), how many edges are there? 1. N 2. N+1 3. N– 1 4. 5 0 / 30 6. 5 Trees 35

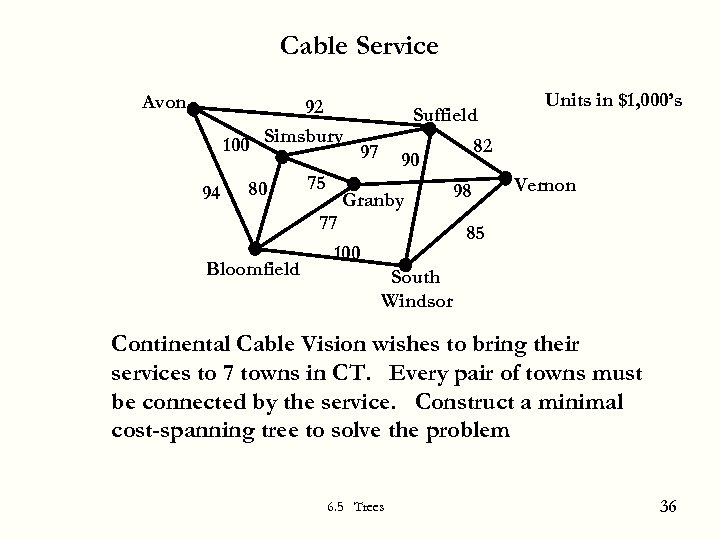Cable Service Avon 92 100 Simsbury 97 94 80 Bloomfield 75 Suffield 82 90 Granby 77 100 Units in $1, 000’s 98 Vernon 85 South Windsor Continental Cable Vision wishes to bring their services to 7 towns in CT. Every pair of towns must be connected by the service. Construct a minimal cost-spanning tree to solve the problem 6. 5 Trees 36

6. 5 Trees 37