Section 2 4 Slope Is a Rate of

Section 2. 4 Slope Is a Rate of Change

Definition Calculate the Rate of Change Definition The ratio of a to b is the fraction is a ratio written as A unit ratio with Example Suppose the sea level increases steadily by 12 inches in the past 4 hours as it approaches high tide. We can compute how much sea level change per hour by finding the unit ratio of the change in sea level to the change in time: Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 2

Definition Calculate the Rate of Change Solution So, sea level increases by 3 inches per hours. • This is an example of rate of change • We say, “The rate of change of sea level with respect to time is 3 inches per hour. ” • The rate of change is constant because sea level increases steadily Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 3

Examples of Rates of Change Calculate the Rate of Change Examples of rates of changes: • The number of members of a club increases by five people per month. • The value of a stock decreases by $2 per week. • The cost of a gallon of gasoline increases by 10¢ per month. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 4

Formula for Rate of Change and Average Rate of Change Calculate the Rate of Change Definition Suppose that a quality y changes steadily form y 1 to y 2 as a quality x changes steadily from x 1 to x 2. Then the rate of change of y with respect to x is the ratio of the change in y to the change in x: If either quantity does not change steadily, then this formula is the average rate of change of y with respect to x. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 5

Finding Rates of Change Calculate the Rate of Change Example 1. The number of fires in U. S. hotels declined approximately steadily from 7100 fires in 1990 to 4200 in 2002. Find the average rate of change of the number of hotel fires per year between 1990 and 2002. Solution Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 6

Finding Rates of Change Calculate the Rate of Change Solution Continued The average rate of change of the number of fires per year was about – 241. 67 fires per year. So, on average, the number of fires declined yearly by about 242 fires. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 7

Finding Rates of Change Calculate the Rate of Change Example Continued 2. In San Bruno, California, the average value of a two-bedroom home is $543 thousand, and the average value of a five-bedroom home is $793. Find the average rate of change of the average value of a home with respect to the number of bedrooms. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 8

Finding Rates of Change Calculate the Rate of Change Solution • Consistent in finding signs of the changes • Assume that number of bedrooms increases form two to five • Assume that the average value increases from $543 thousand to $793 thousand Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 9

Finding Rates of Change Calculate the Rate of Change Solution Continued • Average rate of change of the average value with respect to the number of bedrooms is about $83. 33 thousand per bedroom • Average value increases by about $83. 33 thousand per bedroom Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 10

Increasing and Decreasing Quantities Calculate the Rate of Change Properties Suppose that a quantity p depends on a quantity t: • If p increases steadily as t increases steadily, then the rate of change of p with respect to t is positive • If p decreases steadily as t increases steadily, then the rate of change of p with respect to t is negative Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 11

Comparing Slope with a Rate of Change Slope Is a Rate of Change Example Suppose that a student drives at a constant rate. Let d be the distance (in miles) that the student can drive in t hours. Some values of t and d are shown in the table. 1. Create a scattergram. Then draw a linear model. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 12

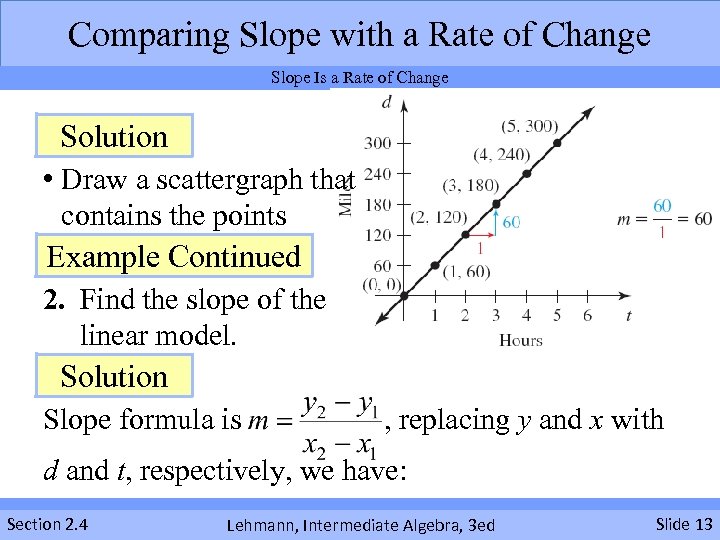Comparing Slope with a Rate of Change Slope Is a Rate of Change Solution • Draw a scattergraph that contains the points Example Continued 2. Find the slope of the linear model. Solution Slope formula is , replacing y and x with d and t, respectively, we have: Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 13

Comparing Slope with a Rate of Change Slope Is a Rate of Change Solution Continued Arbitrarily use the points (2, 120) and (3, 180) to calculate the slope: • The slope is 60 • Checks with calculations shown in the scattergraph Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 14

Comparing Slope with a Rate of Change Slope Is a Rate of Change Example Continued 3. Find the rate of change of distance per hour for each given period. Compare each result with the slope of the linear model. a. From b. From Solution • Calculate rate of change of the distance per hour from Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 15

Comparing Slope with a Rate of Change Slope Is a Rate of Change Solution Continued • The rate of change (60 miles per hour) is equal to the slope (60) • For part b. , calculate the rate of change of distance per hour from Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 16

Comparing Slope with a Rate of Change Slope Is a Rate of Change Solution Continued • The rate of change (60 miles per hour) is equal to the slope (60) Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 17

Slope is a Rate of Change Slope Is a Rate of Change Property If there is a linear relationship between quantities t and p, and if p depends on t, then the slope of the linear model is equal to the rate of change of p with respect to t. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 18

Constant Rate of Change Slope Is a Rate of Change Property Suppose that a quantity p depends on a quantity t: • If there is a linear relationship between t and p, then the rate of change of p with respect to t is constant. • If the rate of change of p with respect to t is constant, then there is a liner relationship between t and p. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 19

Finding a Model Finding an Equation of a Linear Model Example A company’s profit was $10 million in 2005 and has increased by $3 million per year. Let p be the profit (in millions of dollars) in the year that is t years since 2005. 1. Is there a linear relationship between t and p? Solution • Since the profit is a constant $3 million per year, the variables t and p are linearly related Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 20

Finding a Model Finding an Equation of a Linear Model Example Continued 2. Find the p-intercept of a linear model Solution • Profit was $10 million in 2005 • 2005 is 0 years since 2005 • This gives the ordered pair (0, 10) • So, the p-intercept is (0, 10) Example Continued 3. Find the slope of the linear model. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 21

Finding a Model Finding an Equation of a Linear Model Solution • Rate of change of profit per year is $3 million per year • So, the slope of the linear model is 3 Example Continued 4. Find an equation of the linear model. Solution • Since p-intercept is (0, 10) and slope is 3, the linear model is: Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 22

Finding a Model Finding an Equation of a Linear Model Graphing Calculator • Verify the ordered pair (0, 10) • Verify that as the input increases by 1, the output increases by 3 Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 23

Definition: Unit Analysis of a Linear Model Definition We perform a unit analysis of a model’s equations by determining the units of the expression on both sides of the equation. The simplified units of the expressions on both sides of the equation should be the same. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 24

Finding a Model Unit Analysis of a Linear Model Example A driver fills her car’s 12 -gallon gasoline tank and drives as a constant speed. The car consumes 0. 04 gallon per mile. Let G be the number of gallons of gasoline remaining in the tank after she has driven d miles since filling up. 1. Is there a linear relationship between d and G? Solution • Rate of change is a constant – 0. 04 gallons per minute, so d and G are linearly related Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 25

Finding a Model Unit Analysis of a Linear Model Example Continued 2. Find the G-intercept of a linear model. Solution • Tank is full at 12 gallons: ordered pair (0, 12) Example Continued 3. Find the slope of the linear model. Solution • Gasoline remaining in the tank with respect to distance traveled is: Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 26

Finding a Model Unit Analysis of a Linear Model Example Continued 4. Find the equation of the linear model. Solution • Since p-intercept is (0, 12) and slope is – 0. 04, the linear model is: Example Continued 5. Perform a unit analysis of the equation Solution • Here a unit analysis on the equation Section 2. 4 Lehmann, Intermediate Algebra, 3 ed : Slide 27

Finding a Model Unit Analysis of a Linear Model Solution Continued • We use the fact that = 1 to simplify the units of the expression on the right-hand side of the equation: • Units on both sides are gallons: Suggesting correct Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 28

Analyzing a Model Two Variables That Are Approximately Linearly Related Example Yogurt sales (in billions of dollars) in the United States are shown in the table for various years. Let s be yogurt sales (in billions of dollars) in the year that is t years since 2000. A model of the situation is: 1. Use a graphing calculator to draw a scattergram and the model in the same viewing window. Check whether the line comes close to the data. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 29

Analyzing a Model Two Variables That Are Approximately Linearly Related Solution • Draw in the same screen using a graphing calculator • See Sections B. 8 and B. 10 Example Continued 2. What is the slope of the model? What does it mean in this situation? Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 30

Analyzing a Model Two Variables That Are Approximately Linearly Related Solution • which is of the form • Since m is the slope, the slope is 0. 17 • Sales increase by 0. 17 billion dollars per year Example Continue 3. Find the rates of change in sales from one year to the next. Compare the rates of change with the results in Problem 2. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 31

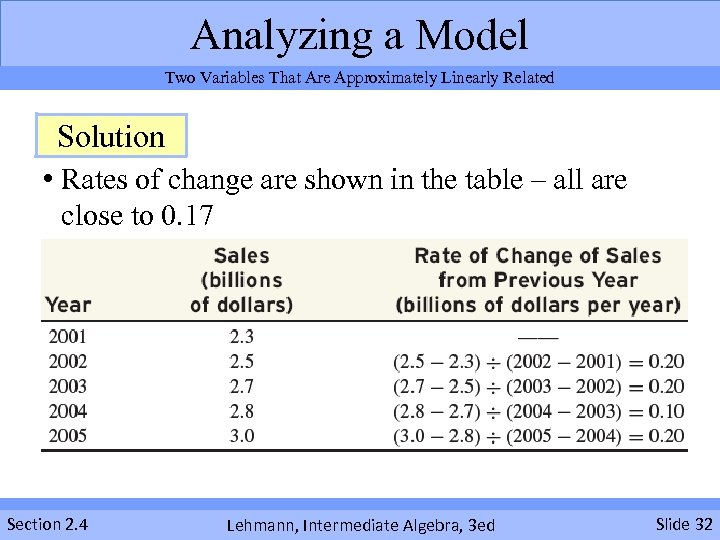Analyzing a Model Two Variables That Are Approximately Linearly Related Solution • Rates of change are shown in the table – all are close to 0. 17 Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 32

Analyzing a Model Two Variables That Are Approximately Linearly Related Example Continue 4. Predict the sales in 2010. Solution • Substitute the input of 10 for t: Property If two quantities t and p are approximately linearly related, and if p depends on t, then the slope of a reasonable linear model is approximately equal to the average rate of change of p with respect to t. Section 2. 4 Lehmann, Intermediate Algebra, 3 ed Slide 33