0ecf90791146fde210c679faddb598c8.ppt
- Количество слайдов: 10

Section 2. 4 ~ Index Numbers Introduction to Probability and Statistics Ms. Young

Sec. 2. 4 Objective n To understand the concept of an index number; particularly how the Consumer Price Index (CPI) is used to measure inflation and make comparisons over different time periods.

Sec. 2. 4 Index Numbers n n We have all heard our elders say things like, “When I was young, this same loaf of bread only cost a nickel” or “It only cost me $8 to fill my tank in 1955” One way to facilitate comparisons of the same thing over time is by using index numbers ¨ n To calculate an index number for a certain product (gas, bread, etc. ), each value is compared to one reference value ¨ n Index numbers are numbers that provide a simple way to compare measurements of the same thing made at different times or in different places Ex. ~ We might call the price in 1975 the reference value in which case the index numbers come from the comparison of each year to 1975 The index numbers are the percentage of the comparison to the reference value written without the percent symbol
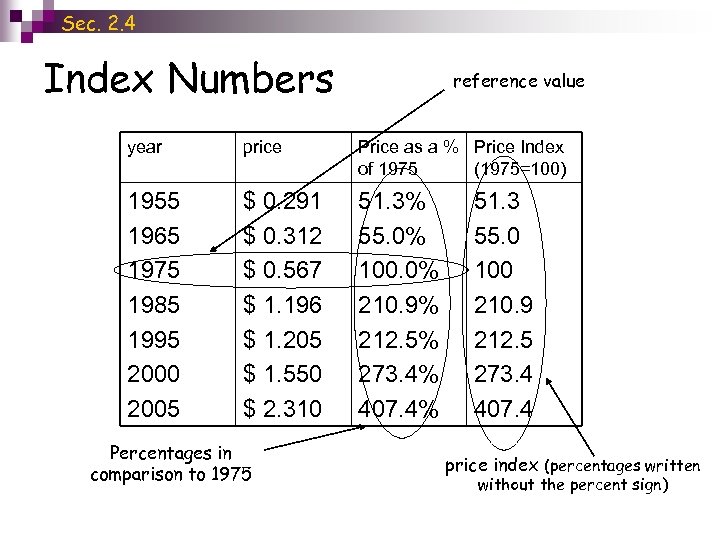
Sec. 2. 4 Index Numbers reference value year price Price as a % Price Index of 1975 (1975=100) 1955 1965 1975 1985 1995 2000 2005 $ 0. 291 $ 0. 312 $ 0. 567 $ 1. 196 $ 1. 205 $ 1. 550 $ 2. 310 51. 3% 55. 0% 100. 0% 210. 9% 212. 5% 273. 4% 407. 4% Percentages in comparison to 1975 51. 3 55. 0 100 210. 9 212. 5 273. 4 407. 4 price index (percentages written without the percent sign)

Sec. 2. 4 Example 1 n Suppose the cost of gasoline today is $2. 79 per gallon. Using the 1975 price as the reference value, find the price index number for gasoline today. ¨ This means that the current price of gas is 492. 1% of the price in 1975 or 4. 921 times the price in 1975 n Or you could even say that it is 392. 1% more than the gas price in 1975

Sec. 2. 4 Making Comparisons with Index Numbers n The index numbers that are reported are in comparison to the reference value, but you can use the index numbers to compare other values as well ¨ Ex. ~ Suppose we want to know how much more expensive gas was in 1995 than in 1965, but 1975 is the reference value. n Since both index values are in comparison to the same reference value (the year 1975), you can just compare them to each other ¨ This means that the 1995 price for gas was 3. 86 times the 1965 price, or 386% of the 1965 price.

Sec. 2. 4 Example 2 n Use the gas index number table to answer the following questions. ¨ a. Suppose that it cost $7. 00 to fill your gas tank in 1975. How much did it cost to buy the same amount of gas in 2005? n n ¨ The index number for 2005 is 407. 4, which means that it was 407. 4% of the price in 1975 or 4. 074 times the price in 1975 If the cost was $7. 00 to fill your gas tank in 1975, then it was $28. 52 ($7 x 4. 074 = $28. 52) in 2005 b. Suppose that it cost $20. 00 to fill your tank in 1995. How much did it cost to buy the same amount of gas in 1955? n n You must first compare the index number in 1955 to that in 1995 The price in 1955 is. 2414 times the price in 1995, so if it cost $20. 00 to fill your tank in 1995, then it cost $4. 83 ($20 x. 2414 = $4. 83) in 1955

Sec. 2. 4 The Consumer Price Index n Inflation – when prices of goods, services, and housing costs increase over time ¨ ¨ n n Deflation would be when prices decrease Ex. ~ As we talked about earlier, the 1995 price of gas was 3. 86 times the 1965 price. This may seem extremely high, but you have to remember that this number is based solely on the price index and doesn’t account for any wage increases Because of inflation, simply comparing the changes in prices for certain items (such as gas) is not very meaningful unless you take other factors into consideration The Consumer Price Index (CPI) is a monthly report that represents an average of prices for a sample of more than 60, 000 goods, services, and housing costs in comparison to a reference value In other words, The Consumer Price Index reports the overall inflation rate in comparison to a certain year (1982 -1984 at this time) ¨ This allows us to compare overall prices at different times ¨ n n Ex. ~ to find out how much higher typical prices were in 2005 than in 1995, you divide the CPI’s for the two years (refer to p. 77 for the report) Based on the CPI, typical prices in 2005 were 1. 28 times those in 1995. In other words, an item that cost $1, 000 in 1995 would cost $1, 280 in 2005

Sec. 2. 4 Example 3 n Suppose you needed $30, 000 to maintain a particular standard of living in 2000. How much would you have needed in 2006 to maintain the same living standard? ¨ Since the CPI is an index value, we can make comparisons the same way we did before: ¨ The cost of living in 2006 is 1. 17 times the cost of living in 2000, so a $30, 000 standard of living would cost $35, 100 ($30, 000 x 1. 17) in 2006

Sec. 2. 4 Adjusting Prices for Inflation n The CPI is also commonly used to make comparisons of salary increases versus the inflation rate ¨ n This value can then be used to examine whether or not a company is paying enough (or too much) in comparison to the average rate of inflation Example 4 ¨ In 1987, the mean salary for major league baseball players was $412, 000. In 2006, it was $2, 867, 000. Compare the increase in mean baseball salaries to the overall rate of inflation measured by the Consumer Price Index. n First compare the Consumer Price Indices for 2006 and 1987: n Next, compare the average baseball salaries for the two years: n By comparing the two values, you can see that while the average inflation rate rose about 77%, the baseball salaries rose about 600% which tells us that the mean baseball salary far surpassed the average rate of inflation!
0ecf90791146fde210c679faddb598c8.ppt