Section 1 6 The Coordinate Plane Distance Midpoint

Section 1. 6: The Coordinate Plane Distance, Midpoint, and Graphing • Distance is amount of space from one place or object to another. – Knowing the distance could be useful when getting gas for your car so you know how many gallons of gas to get for a certain number of miles. • Midpoint is the middle of two points. – Knowing the midpoint of something can be useful when you want to meet someone half way. If you and your friend’s house is 1000 meters away from each other, you can meet them halfway, which is 500 meters. (You can also use landscapes instead of measuring). 1000 meters 500 meters • Graphing on a coordinate plane can be used to show the change of something. – Graphing can come in handy when you want to show the production of a company’s sales over a certain time period.

Chapter 1 -7: Perimeter, Circumference, & Area • • • Perimeter- the sum of all the lengths and sides of a polygon Area- the # of square units a polygon encloses Circumference- perimeter of a circle Real World: Knowing the perimeter, circumference, or area of something can come in handy when baking a cake that needs to be a certain size. For example, if it needs to be round about 36 inches around, you might need to measure the diameter of the pan to get it right. C= 37. 68 4 in. A= s² s b h h C= 3. 14(12) d=12 in P= 4 s s P= 2 b+2 h A= bh b 4 in. d=12 in r Also, if you need a picture frame for your picture, you need to know the perimeter of your picture so you know what size your frame needs to be. P= 2(4) + 2(8) h d C= πd A= πr² C P= 24 in. Inside of frame needs to be 24 in. 4 in 8 in Finally, knowing the area of something would be helpful when creating a banner for something. If you need to make a banner that is 3 feet by 4 feet, you would need to know the area so you know how much material to get. 40 in A= 40(12) A=480 in. of material 12 in

Section 2. 1 -2. 2: Conditional Statements • A conditional is an if-then statement. (hypothesis-conclusion) – If you get 2 pretzels, then you get a free drink. + • Free! = A biconditional is when a conditional and it’s converse are true. (if and only if, or IFF) – Parents might say, “You can go out with your friends if and only if you get a 90 or higher on your math project. ” =

2 -5: Angle Pairs • Vertical angles are two angles whose sides form two pairs of opposite rays. • Adjacent angles are two coplanar angles with a common side, a common vertex, and no common interior points. • Complementary angles have a sum of 90°. • Supplementary angles have a sum of 180°.

Section 3. 2: Angle Pairs Formed by Parallel Lines/ Proving Lines Parallel • Transversal- a line that intersects 2 coplanar lines at 2 distinct points. It forms 8 angles. • Same-side interior angles are supplementary. • 2 lines are parallel if there are congruent: corresponding angles, alternate interior angles, & same-side interior angles. • 2 lines are parallel to each other if they are parallel to the same line. a b c • If two lines are perpendicular to the same line, they are parallel to each other. c a b Transversal l Same-side interior l m n l m ∠ 1 ∠ 2 ∠ 4 ∠ 3 n Corresponding angles are parallel l m Alternate interior angles are parallel ∠ 1 ∠ 2 n l m ∠ 1 ∠ 4 ∠ 2 n If ∠ 1 ≅ , l ||m ∠ 2 If ∠ 2 & ∠ 4 are supplementary, l ||m

Section 3. 3: Triangle and Polygon Classification All angles are congruent. All angles are acute. (<90°) One obtuse angle. (>90°) One right angle. (90°) 4 -sided 5 -sided All sides congruent. At least 2 sides congruent. Square Pentagon 6 -sided Hexagon 7 - sided Heptagon 8 -sided Octagon 9 -sided Nonagon 10 -sided Decagon 12 -sided Dodecagon No sides congruent. hexagon

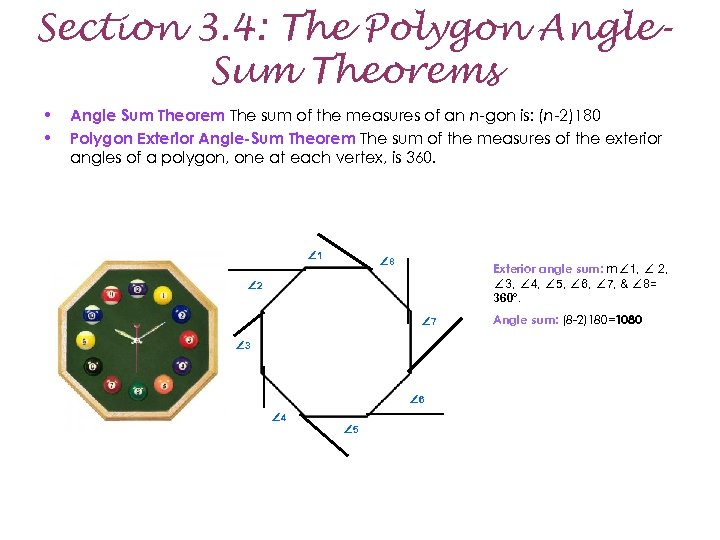Section 3. 4: The Polygon Angle. Sum Theorems • • Angle Sum Theorem The sum of the measures of an n-gon is: (n-2)180 Polygon Exterior Angle-Sum Theorem The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360. ∠ 1 ∠ 8 Exterior angle sum: m∠ 1, ∠ 2, ∠ 3, ∠ 4, ∠ 5, ∠ 6, ∠ 7, & ∠ 8= 360°. ∠ 2 ∠ 7 ∠ 3 ∠ 6 ∠ 4 ∠ 5 Angle sum: (8 -2)180=1080

Section 4. 1: Congruent Figures • Congruent polygons have matching sides, angles, and vertices. B A A corresponds to Y. X W Y Z AC corresponds to YW. C corresponds to W. C AB corresponds to YZ. B corresponds to Z. D BD corresponds to ZX. D corresponds to X. CD corresponds to WX. ∠ A corresponds to ∠ Y. ∠ B corresponds to ∠ Z. ∠ C corresponds to ∠ W. ∠ D corresponds to ∠ X. ABCD ≅ YZWX

4 -5: Isosceles & Equilateral Triangle Properties Isosceles • • Congruent sides of an isosceles triangle are its legs, which form the vertex angle Base is the other side. Other two angles are the base angles. If two sides of a triangle are congruent, then the angles and sides opposite those are congruent. The bisector of the vertex angle is the perpendicular bisector of the base. Vertex Angle C Base A Scalene • If a triangle is equilateral, it is equiangular. • If a triangle is equiangular, it is equilateral. B D Base Angles