Second generation geometry compression Edgebreaker is fast simple

Second generation geometry compression: Edgebreaker is fast, simple, and effective Rossignac, Szymczak, King, Safonova Gumhold Isenberg&Snoeyink Coors Lopes Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 1

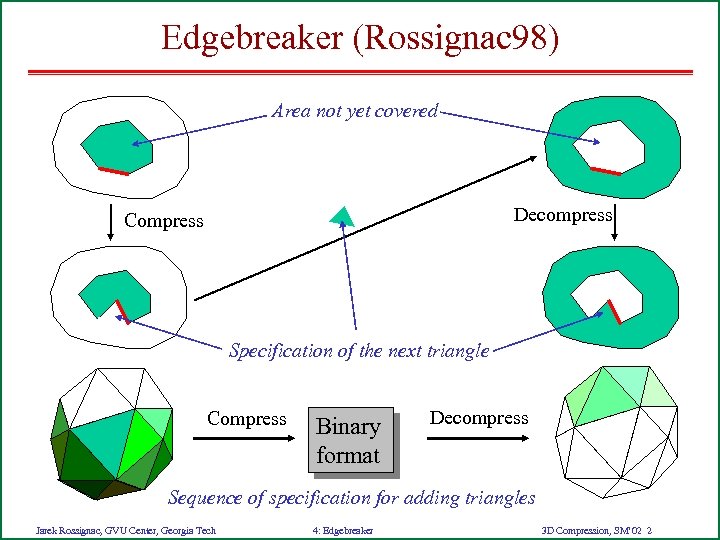
Edgebreaker (Rossignac 98) Area not yet covered Decompress Compress Specification of the next triangle Compress Binary format Decompress Sequence of specification for adding triangles Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 2

Same spiraling traversal as TS-MPEG 4 Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 3

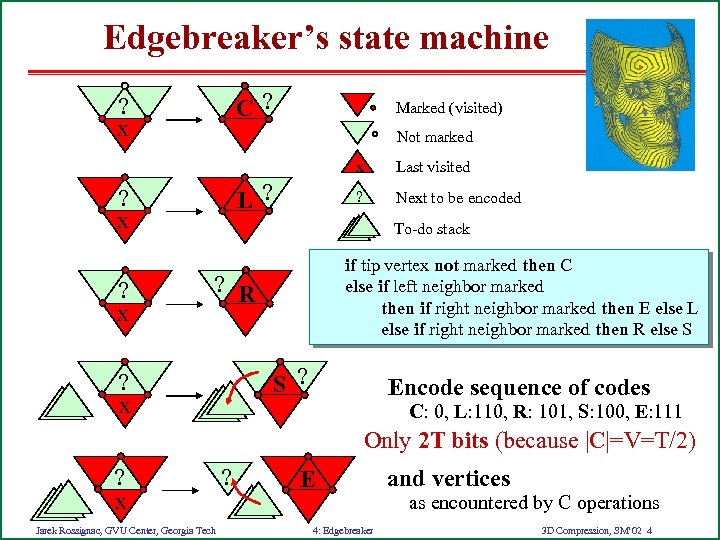
Edgebreaker’s state machine C? ? x Marked (visited) Not marked x ? L? ? x Last visited Next to be encoded To-do stack if tip vertex not marked then C else if left neighbor marked then if right neighbor marked then E else L else if right neighbor marked then R else S ? R S ? ? x Encode sequence of codes C: 0, L: 110, R: 101, S: 100, E: 111 Only 2 T bits (because |C|=V=T/2) ? x Jarek Rossignac, GVU Center, Georgia Tech ? E 4: Edgebreaker and vertices as encountered by C operations 3 D Compression, SM’ 02 4

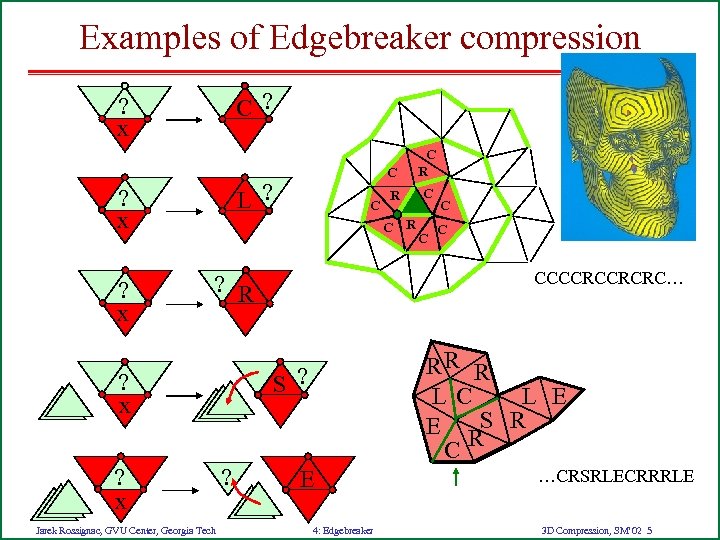
Examples of Edgebreaker compression C ? ? x L ? ? x C C C R R C C R ? x Jarek Rossignac, GVU Center, Georgia Tech RR R LC L E E RS R C S ? ? C CCCCRCCRCRC… ? R ? x C C E 4: Edgebreaker …CRSRLECRRRLE 3 D Compression, SM’ 02 5

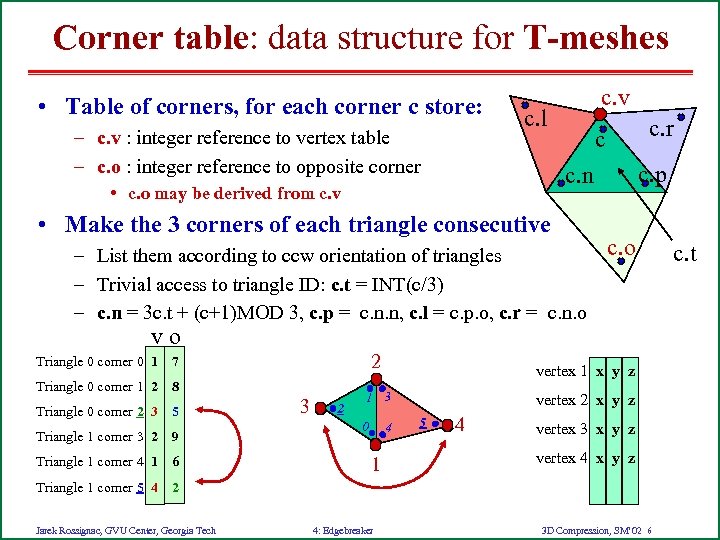
Corner table: data structure for T-meshes • Table of corners, for each corner c store: – c. v : integer reference to vertex table – c. o : integer reference to opposite corner c. v c. l c. r c c. p c. n • c. o may be derived from c. v • Make the 3 corners of each triangle consecutive – List them according to ccw orientation of triangles – Trivial access to triangle ID: c. t = INT(c/3) – c. n = 3 c. t + (c+1)MOD 3, c. p = c. n. n, c. l = c. p. o, c. r = c. n. o c. o vo Triangle 0 corner 0 1 Triangle 0 corner 1 2 2 7 8 Triangle 0 corner 2 3 5 Triangle 1 corner 3 2 9 Triangle 1 corner 4 1 6 3 2 vertex 1 x y z 1 3 0 4 1 vertex 2 x y z 5 4 vertex 3 x y z vertex 4 x y z Triangle 1 corner 5 4 2 Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 6 c. t

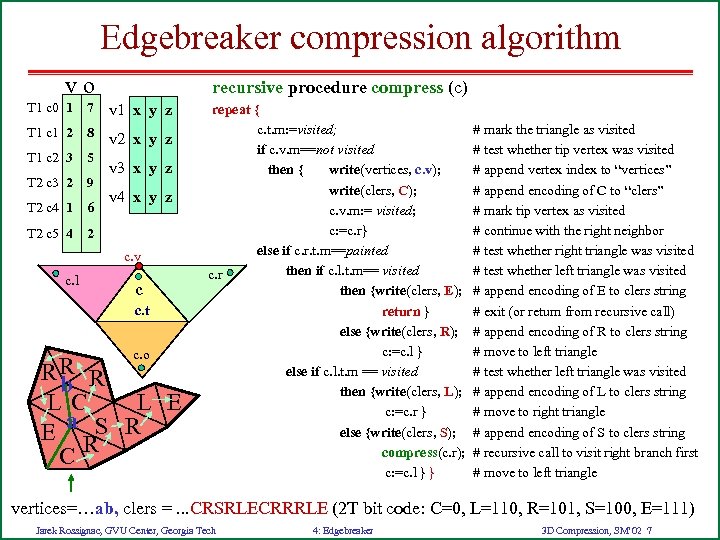
Edgebreaker compression algorithm vo recursive procedure compress (c) T 1 c 0 1 7 v 1 x y z T 1 c 1 2 8 v 2 x y z T 1 c 2 3 5 T 2 c 3 2 9 T 2 c 4 1 6 v 3 x y z v 4 x y z T 2 c 5 4 2 c. v c. l c c. t c. o RR R b LC L E E a RS R C repeat { c. t. m: =visited; if c. v. m==not visited then { write(vertices, c. v); write(clers, C); c. v. m: = visited; c: =c. r} else if c. r. t. m==painted then if c. l. t. m== visited c. r then {write(clers, E); return } else {write(clers, R); c: =c. l } else if c. l. t. m == visited then {write(clers, L); c: =c. r } else {write(clers, S); compress(c. r); c: =c. l } } # mark the triangle as visited # test whether tip vertex was visited # append vertex index to “vertices” # append encoding of C to “clers” # mark tip vertex as visited # continue with the right neighbor # test whether right triangle was visited # test whether left triangle was visited # append encoding of E to clers string # exit (or return from recursive call) # append encoding of R to clers string # move to left triangle # test whether left triangle was visited # append encoding of L to clers string # move to right triangle # append encoding of S to clers string # recursive call to visit right branch first # move to left triangle vertices=…ab, clers =. . . CRSRLECRRRLE (2 T bit code: C=0, L=110, R=101, S=100, E=111) Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 7

Decompression Receive the CLERS sequence Decode it Construct the triangle tree Decode&reconstruct vertices …CRSRLECRRRLE RR R LC L E S R E CR How to zip up the cracks? Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 8

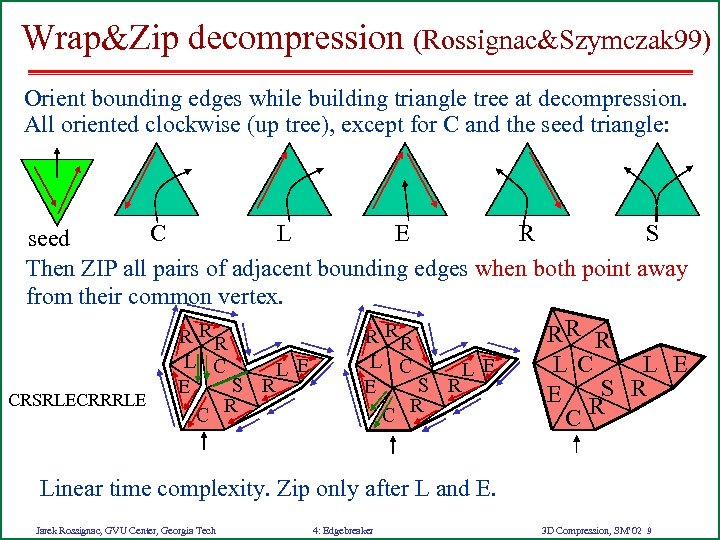
Wrap&Zip decompression (Rossignac&Szymczak 99) Orient bounding edges while building triangle tree at decompression. All oriented clockwise (up tree), except for C and the seed triangle: C L E R S seed Then ZIP all pairs of adjacent bounding edges when both point away from their common vertex. RR RR CRSRLECRRRLE R L C L E S R E R C LC L E E RS R C Linear time complexity. Zip only after L and E. Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 9

Wrap&Zip properties • Only L and E require checking whether zipping is possible – No new zipping is made possible by C, R, S • • • L creates at most one zip (one pair of edges, no iteration) E operation creates at least 2 zips # of zipping operations = # of edges in vertex tree An edge can only be tried and rejected for zipping only once Wrap&Zip has linear time complexity (very fast in practice) R RR L C L E S R E R C Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 10

Spirale Reversi (Isenburg&Snoeyink 99) • “Spirale Reversi: Reverse decoding of the Edgebreaker encoding” • Decompression for Edgebreaker similar to Wrap&Zip • Reads CLERS string backward – Reconstructs mesh backwards – Assigns vertices before the C operation defines them Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 11

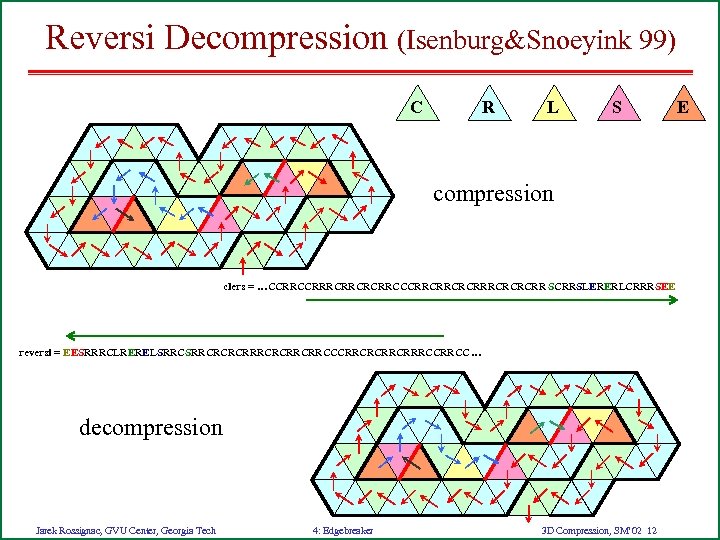
Reversi Decompression (Isenburg&Snoeyink 99) C R L S compression clers = …CCRRRCRRCCCRRCRRCRCRCRR SCRRSLERERLCRRRSEE reversi = EESRRRCLRERELSRRCRCRCRRCRRCCCRRCRRRCC … decompression Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 12 E

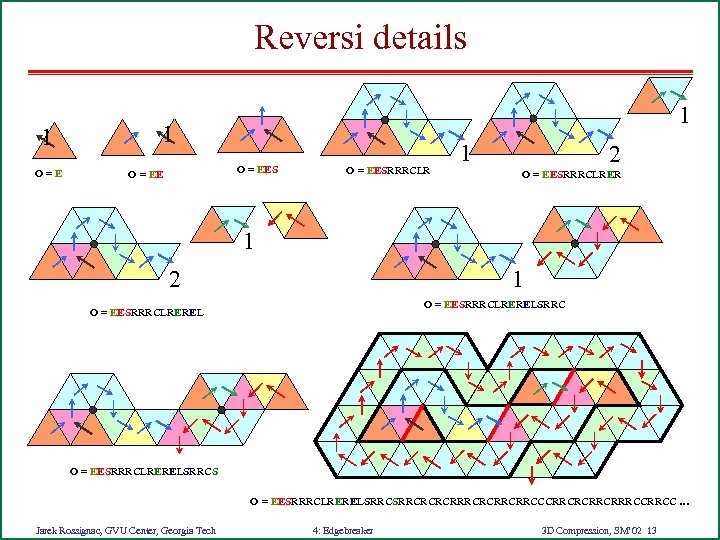
Reversi details 1 O=E 1 1 O = EESRRRCLR 1 2 O = EESRRRCLRER 1 1 2 O = EESRRRCLRERELSRRCS O = EESRRRCLRERELSRRCRCRCRRCRRCCCRRCRRRCC … Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 13

Expected/measured results of Edgebreaker • Expected 1. 7 T bit and guaranteed 2. 0 T bit code – CL and CE combinations are impossible – Use a shorter code for S (11) and R (10) when they follow a C – On average 36% of symbols are R. Half of them follow a C • Expected 1. 3 T to 1. 6 T bits, guaranteed 2. 0 T bits – – Encode CC, CS, CR pairs as single symbols After even # of Cs: CR (01), CC (00), CS (1101), R (10), S(1111) L (1110), E (1100) Stanford Bunny: 1. 3 T bits, Delaunay triangulation: 1. 6 T bits • Measured entropy codes 0. 91 to 1. 26 T bits – – Huffman code: all words start with a consecutive sequence of C Bunny: 173 words, 0. 85 T bits for Huffman codes, 0. 91 T bits total Large model: 1, 400 word dictionary (32 Kb table, large part is fixed) Gzip on the result improves them by 2% Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 14

Edgebreaker + Wrap&Zip Results • Compress: Visit&mark triangles, encode CLERS ops, encode vertices • Decode: Build triangle tree, orient free edges, zip, label & decode vertices • Compression results for connectivity information – Guaranteed 2 T bits for all meshes homeomorphic to a sphere • C: 0, L: 110, R: 101, S: 100, E: 111 (|C|=V=T/2) – Measured entropy code: about 1 T bits (dictionary not included) • Publications (http: //www. gvu. gatech. edu/~jarek/papers) – Rossignac, Edgebreaker Compression, IEEE TVCG’ 99 • Sigma Xi Award for Best Paper by Georgia Tech faculty published in 1999 – Rossignac&Szymczak, Wrap&zip, CGTA’ 99 – King&Rossignac: Guaranteed 3. 67 V bit encoding. . . , CCCG’ 99 – Szymczak&King&Rossignac: Compression of regular meshes, CCCG’ 00 Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 15

Edgebreaker Results • Compression results for connectivity information – Guaranteed 2 T bits, entropy down to 0. 9 T bits for large models – Source code available: 3 page detailed pseudo-code, arrays of integers, fast • http: //www. gvu. gatech. edu/~jarek/edgebreaker/eb • Publications <http: //www. gvu. gatech. edu/~jarek/papers> – Rossignac, Edgebreaker Compression, IEEE TVCG’ 99 • Sigma Xi Best Paper Award – – Rossignac&Szymczak, Wrap&zip, CGTA’ 99 King&Rossignac: Guaranteed 3. 67 V bit encoding. . . , CCCG’ 99 Szymczak&King&Rossignac: Mostly regular meshes, CCCG’ 00 …. Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 16

Edgebreaker extensions and improvements • Better compression – Tighter guaranteed upper bound (King&Rossignac, Gumhold): 1. 80 T bits – Quadrilateral meshes (with Szymczak and King): 1. 34 T bits – Sufficiently regular meshes (with Szymczak and King): 0. 81 T bits guaranteed • Topological extensions – Non manifold solids (with Cardoze) – Handles (with Safonova, Szymczak, Coors, and Lopes) – Holes (with Safonova) • Geometry – Optimal quantization (with King and Szymczak): best B and T – Better predictors from connectivity and neighbors (with Coors) • Higher dimension – Tetrahedra for FEM (with Szymczak): 7 T bits (prior to entropy) – Pentatopes for 4 D simulations (with Szymczak, and with Snoeyink) • Progressive and error-resilient – Compressed batches of vertex-split upgrades (with Pajarola): 3. 5 T bits (total) – Tetrahedra (with Pajarola and Szymczak): 5 T bits (after entropy) Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 17

Guaranteed 1. 84 T bit (King&Rossignac 99) • “Guaranteed 3. 67 v bits encoding of planar triangle graphs” – Proc. 11 th Canadian Conference on Computational Geometry, August 1999 • Encoding of symbols that follow a C – C is 0, S is 10, R is 11 • 3 possible encoding systems for symbols that do not follow a C – Code I: C is 0, S is 100, R is 101, L is 110, E is 111 – Code II: C is 00, S is 111, R is 10, L is 110, E is 01 – Code III: C is 00, S is 010, R is 011, L is 10, E is 11 • One of these 3 codes takes less than (2 -1/6)T bits – Use a 2 -bit switch to identify which code is used for each model • Further constraints (Gumhold 00): 1. 80 T bits guaranteed – E is impossible after C, CCR, … – Because they have increased the length of the bounding loop to more than 3 Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 18

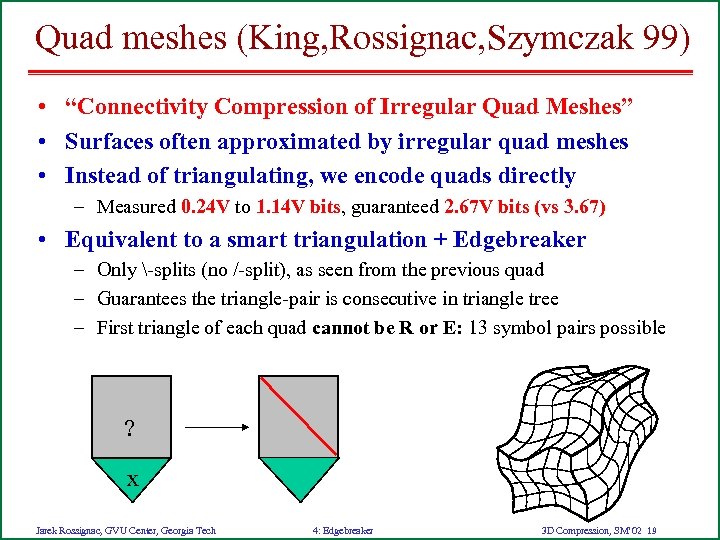
Quad meshes (King, Rossignac, Szymczak 99) • “Connectivity Compression of Irregular Quad Meshes” • Surfaces often approximated by irregular quad meshes • Instead of triangulating, we encode quads directly – Measured 0. 24 V to 1. 14 V bits, guaranteed 2. 67 V bits (vs 3. 67) • Equivalent to a smart triangulation + Edgebreaker – Only -splits (no /-split), as seen from the previous quad – Guarantees the triangle-pair is consecutive in triangle tree – First triangle of each quad cannot be R or E: 13 symbol pairs possible ? x Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 19

Improved Edgebreaker code (Gumhold 00) • “New bounds on the encoding of planar triangulations” – Siggraph course notes on “ 3 D Geometry Compression” • 1. 8 T bits guaranteed • Exploits the length of the outer boundary of T-patch (>2) – Not convenient for treating non-manifolds (See later) • CE is impossible – Was at least 3, C increased it to at least 4, can’t have an E • CCRE is impossible – Was at least 3, CC increased it to at least 5, R reduced it by 1, can’t have an E • These constraints impact the probability of the next symbol and improve coding Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 20

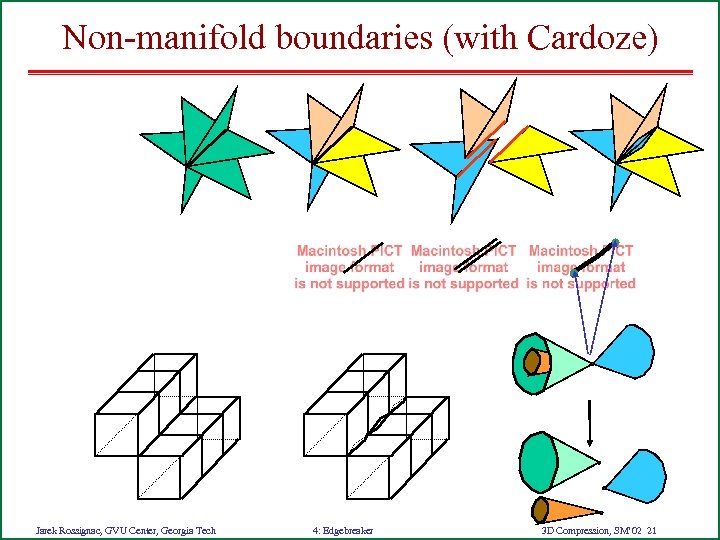
Non-manifold boundaries (with Cardoze) Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 21

Holes (with Safonova) • Many meshes have holes • Plug hole with a triangle fan (Touma&Gotsman’ 98) • Encode identifiers for dummy vertices – HLog(v) bits • The boundary of holes may by non-manfold • What is a hole? Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 22

Handles (with Lopes and Safonova) Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 23

Connectivity compression: An new problem? • Use vertex permutation to encode incidence – • Compression of the connectivity graph (planar triangle graph) – – – • Denny, Sohler: Encoding a triangulation as a permutation of its point set, CCCG, 97 Itai, Rodeh: Representation of graphs, Acta Informatica, 82 Turan: On the succinct representation of graphs, Discrete Applied Math, 84 Naor: Succinct representation of general unlabeled graphs, Discrete Applied Math, 90 Keeler, Westbrook: Short encoding of planar graphs and maps, Discrete Applied Math, 93 Deering: Geometry Compression, Siggraph, 95 Taubin, Rossignac: Geometric compression through topological surgery, ACM To. G, 98 Taubin, Horn, Lazarus, Rossignac: Geometry coding and VRML, Proc. IEEE, 98 Touma, Gotsman: Triangle Mesh Compression, GI, 98 Gumbold, Straßer: Realtime Compression of Triangle Mesh Connectivity, Siggraph, 98 Rossignac: Edgebreaker: Compressing the incidence graph of triangle meshes, TVCG, 99 Rossignac, Szymczak: Wrap&Zip: Linear decompression of triangle meshes, CGTA, 99 Szymczak, Rossignac: Grow&Fold: Compression of tetrahedral meshes, ACM SM, 99 Compressed inverse of progressive simplification steps or batches – – Hoppe: Progressive meshes, Siggraph, 96 Taubin, Gueziec, Horn, Lazarus: Progressive forest split compression, Siggraph, 98 Pajarola, Rossignac: Compressed Progressive Meshes, IEEE TVCG 99 Pajarola, Szymczak, Rossignac: Implant. Spray: Compressed Tetrahedral Meshes, VIS 99 Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker 3 D Compression, SM’ 02 24

Edgebereaker compression contributors Safonova: Holes, implementation Szymczak: Decompression Rossignac: Edgebreaker King: Improved code, quads Isenburg (UCS): Spirale Reversi Gotsman (Israel): Polygons Lopes (Brasil): Handles Coors (Germany): Prediction Jarek Rossignac, GVU Center, Georgia Tech 4: Edgebreaker Gumhold (Germany): Better bounds 3 D Compression, SM’ 02 25