Сечения тетраэдра Взаимное расположение плоскости и многогранника

Сечения тетраэдра

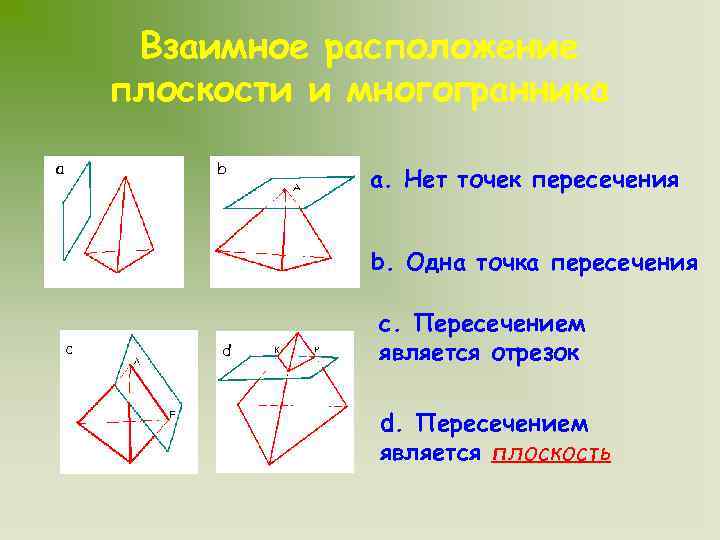Взаимное расположение плоскости и многогранника a b a. Нет точек пересечения b. Одна точка пересечения c d c. Пересечением является отрезок d. Пересечением является плоскость

Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью

МЕТОД СЛЕДОВ ЗАДАЧА № 1 Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, P. Известно, что N SC, P BC

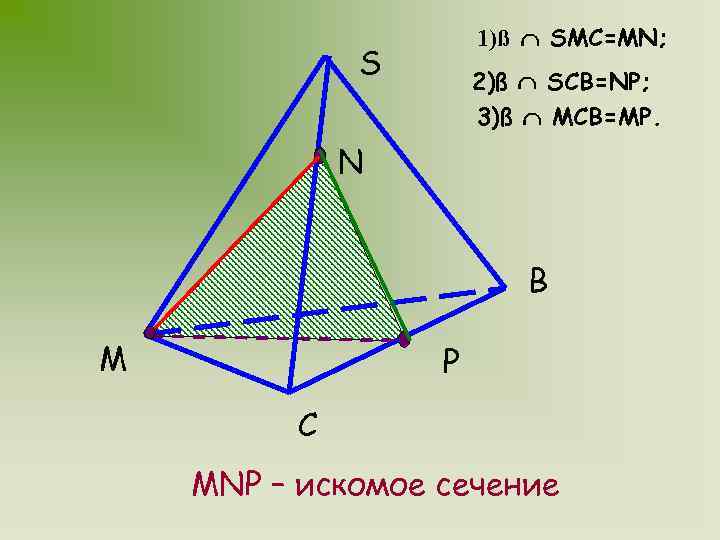1)ß SMC=MN; S 2)ß SCB=NP; 3)ß MCB=MP. N B M P C MNP – искомое сечение

МЕТОД СЛЕДОВ ЗАДАЧА № 2 Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, P. Известно, что N SMC P MSB

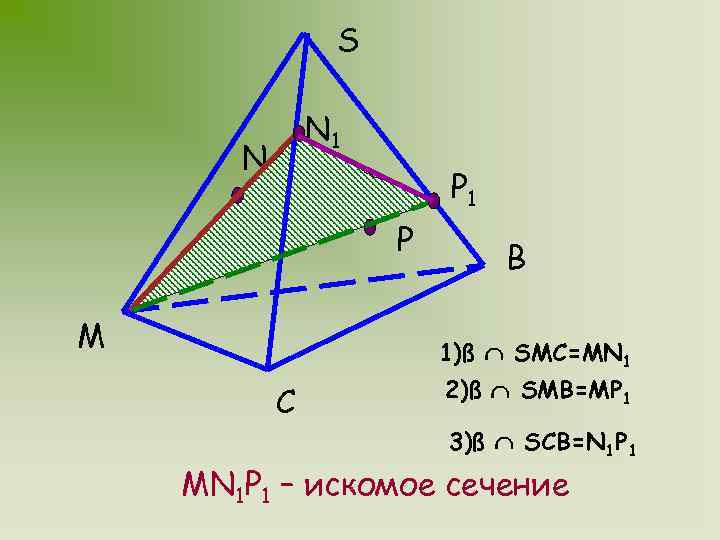S N 1 N P 1 P M B 1)ß SMC=MN 1 C 2)ß SMB=MP 1 3)ß SCB=N 1 P 1 MN 1 P 1 – искомое сечение

МЕТОД СЛЕДОВ ЗАДАЧА № 3 Дан тетраэдр SMCB. Постройте сечение тетраэдра плоскостью, проходящей через точки M, N, P. Известно, что N AB, P AD, M BC

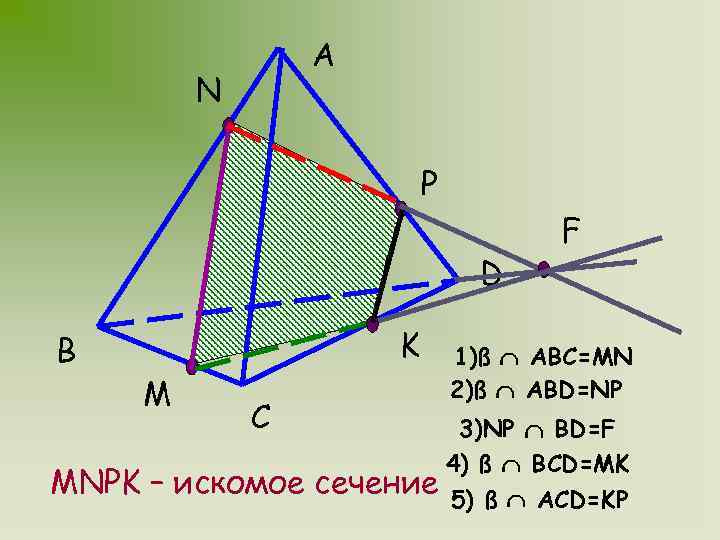A N P D B K M C MNPK – искомое F 1)ß ABC=MN 2)ß ABD=NP 3)NP BD=F 4) ß BCD=MK сечение 5) ß ACD=KP