Sec 12 5 Circles in the Coordinate

Sec. 12 – 5 Circles in the Coordinate Plane Of Lions Quarrel A flying squirrel

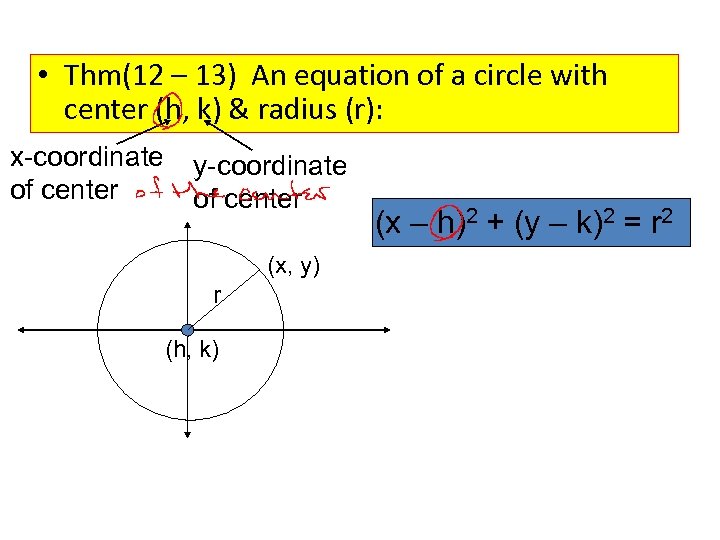• Thm(12 – 13) An equation of a circle with center (h, k) & radius (r): x-coordinate of center y-coordinate of center (x, y) r (h, k) (x – h)2 + (y – k)2 = r 2

Ex. 1: • Write the standard equation of a circle with center (8, 1) and radius of √ 5. Graph it. (x – h)2 + (y – k)2 = r 2 (x – (-8))2 + (y – 1)2 = (√ 5)2 √ 5 1 -8 (x + 8)2 + (y – 1)2 = 5

Ex. 2: Find the center and radius of a circle with the following equation. • Equation: (x – 4)2 + (y + 2)2 = 25 – Center (4, -2) – Radius = 5

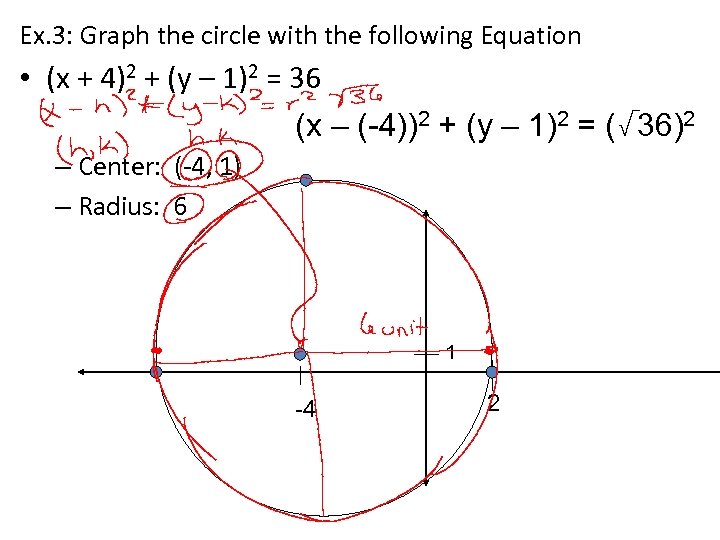Ex. 3: Graph the circle with the following Equation • (x + 4)2 + (y – 1)2 = 36 (x – (-4))2 + (y – 1)2 = (√ 36)2 – Center: (-4, 1) – Radius: 6 1 -4 2

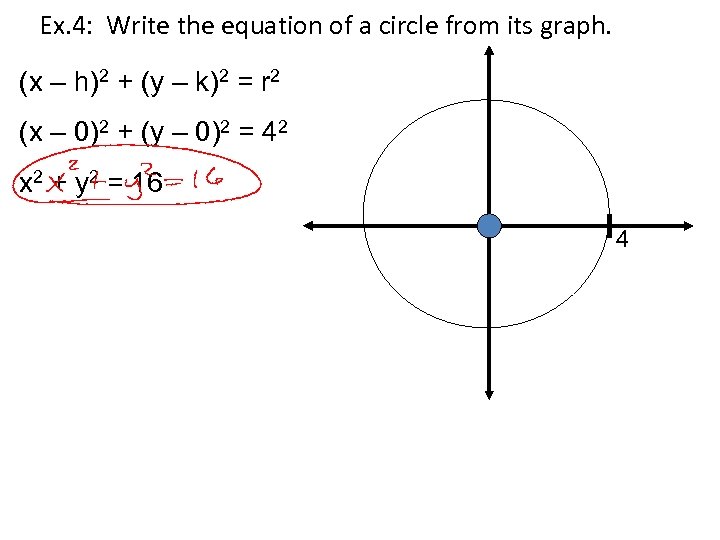Ex. 4: Write the equation of a circle from its graph. (x – h)2 + (y – k)2 = r 2 (x – 0)2 + (y – 0)2 = 42 x 2 + y 2 = 16 4

Ex. 4: Write the standard equation of a circle with center (5, 8) & passes through point (-15, -13). h k x y (x – h)2 + (y – k)2 = r 2 (-15 – 5)2 + (-13 - 8)2 = r 2 (x – 5)2 + (y – 8)2 = 292 -202 + -212 = r 2 400 + 441 = r 2 841 = r 2 29 = r (x – 5)2 + (y – 8)2 = 841

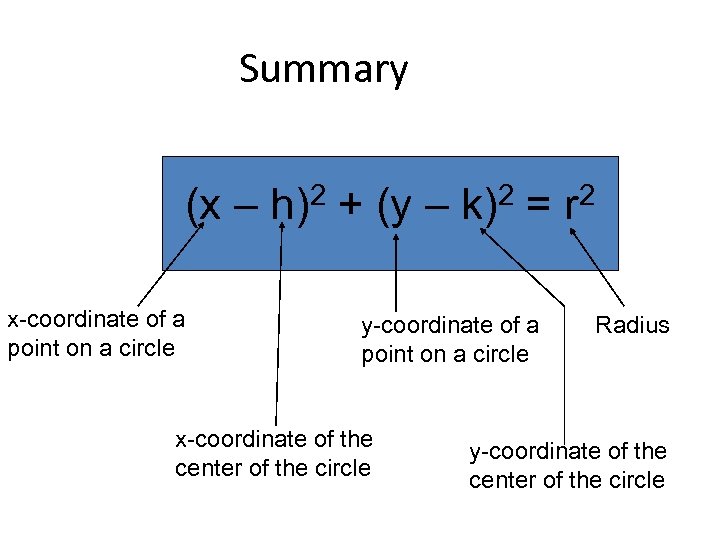Summary (x – h)2 + (y – k)2 = r 2 x-coordinate of a point on a circle y-coordinate of a point on a circle x-coordinate of the center of the circle Radius y-coordinate of the center of the circle

Homework: p. 697 #1 -21 odd, 27 -33 odd House Wheat This Hound How sweet the sound