Scientific session DNIT of the RAS New optimization

Scientific session DNIT of the RAS New optimization coding theory and its applied achievements 24. 04. 2008. V. V. Zolotarev, SRI RAS V. V. Zolotarev. The coding theory

The main fundamental scientific • Theoretical basis of unequivocal exact • • problem of transition from theorem restoration of an analog signal is theanalog of Communications(connections readout of academician V. A. Kotelnikov. ) and computer science At transition of our technological civilization To digital to transmission and storage of the information to a discrete form the main requirement to such • Maintenance of a high their systems, becomes level conformity to Shannon of reliability of formation, theorem. transfer and processing, storage of figures. In this case it is possible to restore always in • Means of the decision of this problem methods of the receiver- the digital message deformed in a theory of noiseproof channel, with as much as necessary small error coding probability if the length of the code block will grow. This theorem has begun the modern of coding. V. V. Zolotarev. The coding theory 2

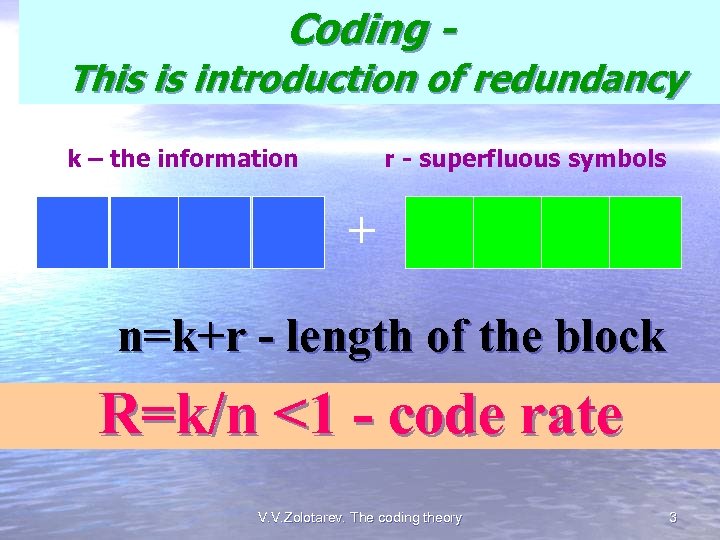Coding -This introduction of This is introduction of redundancy K - the k information – the information Rr--superfluous symbols + + n=k+r - length of the block R=k/n <1 --code speed <1 code rate R=k/n V. V. Zolotarev. The coding theory 3

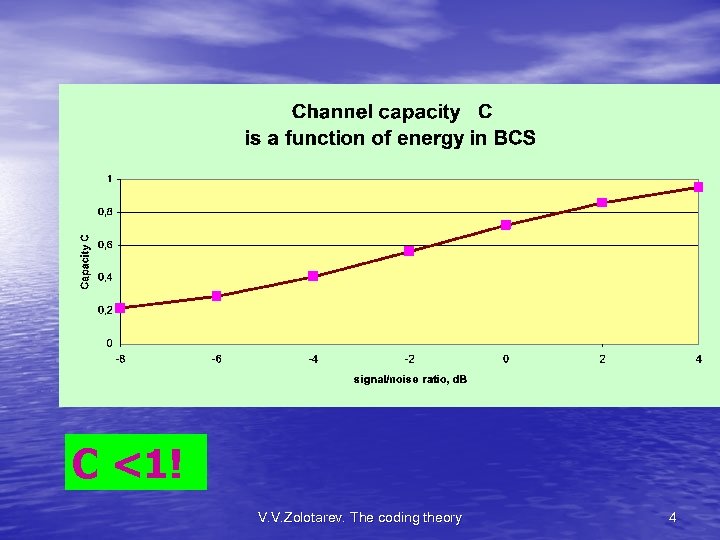WIT H C <1! V. V. Zolotarev. The coding theory 4

The basic restriction of the Information Theory for coding • Always condition R

What is necessary for codes in communication networks? • It is - a code gain, CG!, - a measure of signal • • energy effectiveness increase. Now every one additional d. B in CG gives in communication networks economic benefit in many millions dollars! Resource ЭВК can be realized at ERS for decrease of aerials sizes, and also for increase in speed, reliability and distance of communication. It is extremely important for satellite communication systems such as VSAT, and also projects micro- and nano- satellites or other high-speed communication systems. It is achieved only by correct fast mathematical processing of a digital stream! V. V. Zolotarev. The coding theory 6

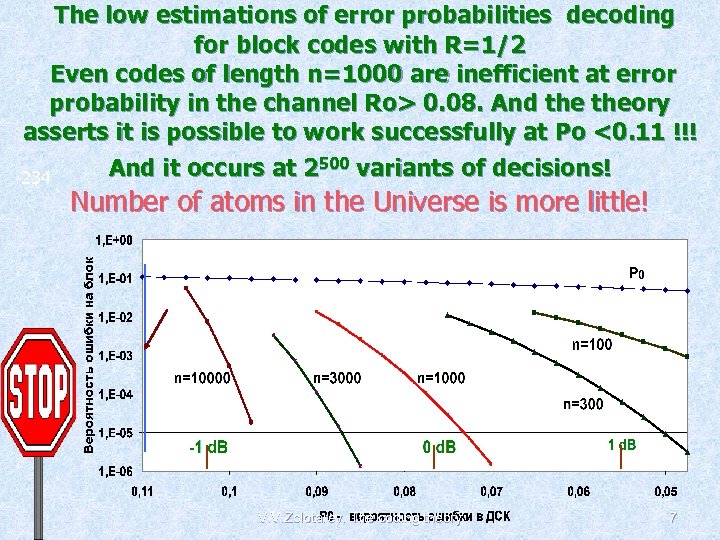The low estimations of error probabilities decoding for block codes with R=1/2 Even codes of length n=1000 are inefficient at error probability in the channel Ro> 0. 08. And theory asserts it is possible to work successfully at Ро <0. 11 !!! And it occurs at 2500 variants of decisions! 234 Number of atoms in the Universe is more little! V. V. Zolotarev. The coding theory 7

Complexity of decoders for different codes with length n en VA !!! MTD Discr. algebra V. V. Zolotarev. The coding theory 8

The block multithreshold decoder for a code with R=1/2, d=5 and I iterations MTD, complexity-N~d*I*n V. V. Zolotarev. The coding theory 9

The reasons of high efficiency new MTD a method • 1. Procedure is applied special very easy for • • realization iterative оптимизационная. 2. Special codes with a minimum level of grouping of mistakes - too a method of optimization are constructed. 3. Process of many hundreds parameters special optimization in the decoder was realized. Problems 1 and 2 - “are very difficult" The problem 3 - has not appeared at all V. V. Zolotarev. The coding theory 10

Minimum of calculations at decoding - in MTD! (Number of operations per bit, soft realization) Usually: N 1 ~ d*I, - product and in MTD: only N 2~d+I, - the sum of key parameters d and I. It is in ~100 times easier and faster than, for example, at use of a turbo codes! It was realized in special TV-system. V. V. Zolotarev. The coding theory 11

Hardware realization MTD at VLSI 1. MTD will consist almost completely of store elements or shift registers. These are the fastest elements in VLSI. The share of other elements in MTD is less than 1 %. 2. MTD may be absolutely parallel one step algorithm. For this reason MTD for some values of parameters approximately in 1000 times faster, than for example, a turbo decoders. A delay - as for the elementary 2 input key - absolute minimum. 3. Realization: throughput: up to 1, 6 Gb/s, and CG = 7 - 9, 5 d. B V. V. Zolotarev. The coding theory 12

Chipset of the MTD decoder at Xilinx for channels with speeds up to 150 Mb / s V. V. Zolotarev. The coding theory 13

Multithreshold decoder (MTD) for satellite and space channels, raises efficiency of their use in 3 -10 times, including for EDS. Simple MODEL MTD at Altera for channels up to 640 Mbit / s. The method can work at information speeds up to 1, 6 Gbit / s MTD for the Space! V. V. Zolotarev. The coding theory 14

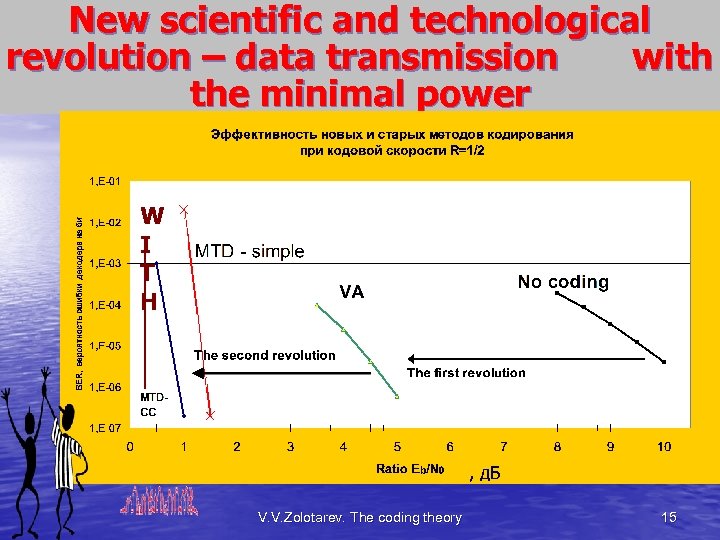New scientific and technological revolution – data transmission with the minimal power W I T H , д. Б V. V. Zolotarev. The coding theory 15

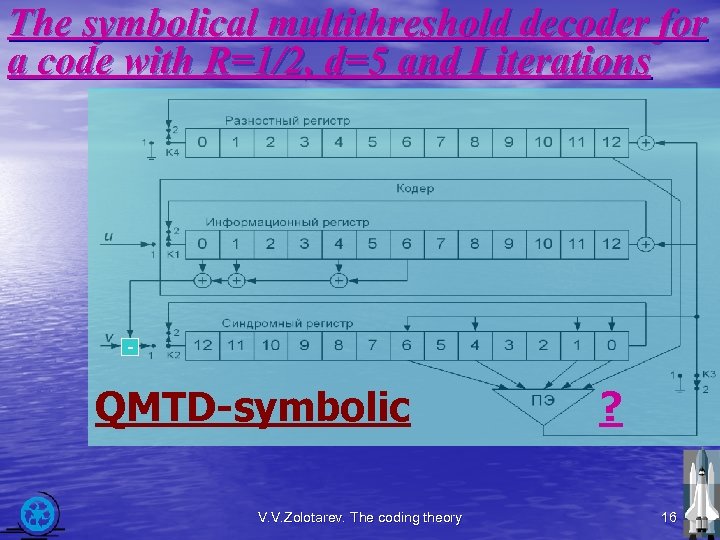The symbolical multithreshold decoder for a code with R=1/2, d=5 and I iterations - QMTD-symbolic V. V. Zolotarev. The coding theory ? 16

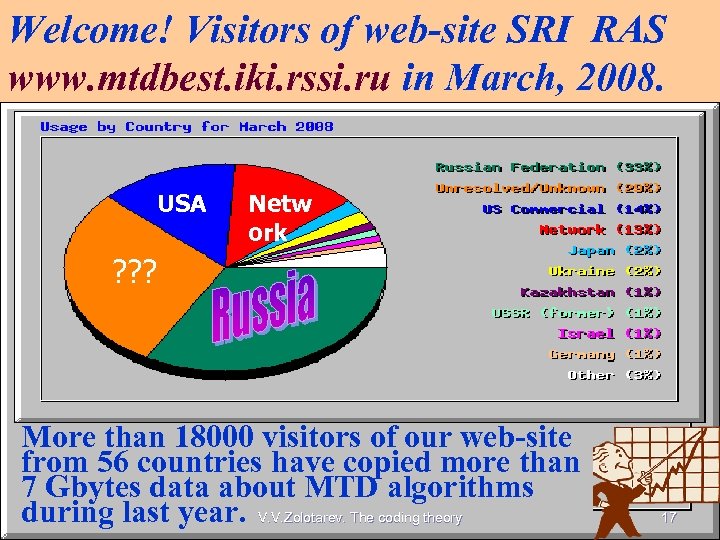Welcome! Visitors of web-site SRI RAS www. mtdbest. iki. rssi. ru in March, 2008. USA Netw ork ? ? ? More than 18000 visitors of our web-site from 56 countries have copied more than 7 Gbytes data about MTD algorithms during last year. V. V. Zolotarev. The coding theory 17

Chipset MTD decoder at ALTERA basis V. V. Zolotarev. The coding theory 18

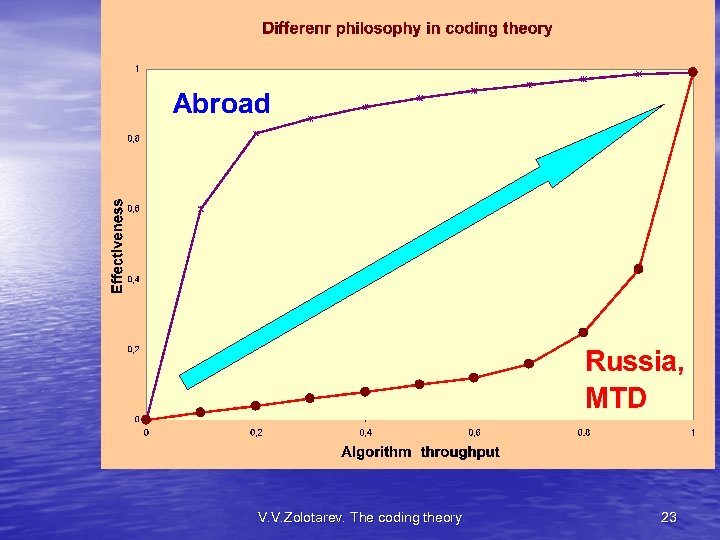
Conclusions 1. We have opened iterative MTD algorithms 35 years ago. 2. Complexity of the soft versions MTD is an absolute known minimum of calculations. A difference with other codes is ~100 times! The rare case in theory! We outstrip all countries ~ 7 ÷ 10 years. 3. Hard MTD are faster than a other codes ~1000 times! 4. Decisions MTD are almost always optimum even at the big noise level. 5. MTD - the absolute leader by criteria "complexity - efficiency". It is created in Russia! 6. Nonbinary codes for MTD - the most unique discovery in the coding theory during last 30 years. They are unknown abroad! The Russian scientific school - again in the group of world leaders in theory! V. V. Zolotarev. The coding theory 19

SRI of the Russian Academy of Sciences in Moscow w. ph. : (495) 333 45 45, www. mtdbest. iki. rssi. ru, -mail: zolotasd@yandex. ru e mobil: +7 916 518 86 28 V. V. Zolotarev 24. 04. 2008. V. V. Zolotarev. The coding theory 20

Furthere are help slides - appendices to the report V. V. Zolotarev. The coding theory 21

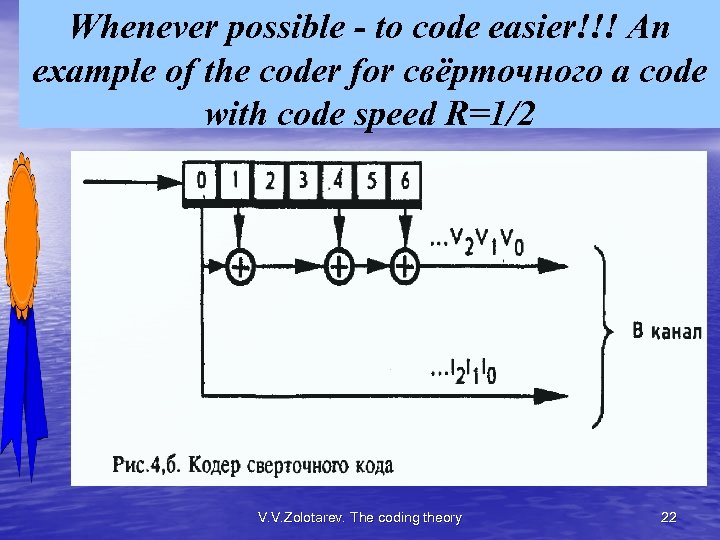Whenever possible - to code easier!!! An example of the coder for свёрточного a code with code speed R=1/2 V. V. Zolotarev. The coding theory 22

V. V. Zolotarev. The coding theory 23

Complexity of various algorithms of decoding Codes and algorithms Algorithm Viterbi Algebraic codes Turbo codes Low dencity parity codes Majority codes- only in Russia - MTD which almost always converges to optimum (total search!) the decision, but with linear complexity V. V. Zolotarev. The coding theory Complexity 2 n n 2 C 1*n C 2*n C 3*n С 3

Convolutionale multithreshold decoder for a code with R=1/2, d=5 and 3 iterations Fig. 1. The multithreshold decoder сверточного JUICE with R=1/2, d=5 and n. A=14 V. V. Zolotarev. The coding theory 25

The reasons of high efficiency new МПД a method • 1. Procedure is applied special very easy for realization iterative оптимизационная. • 2. Special codes with a minimum level of grouping of mistakes - a method of optimization are constructed. • 3. Special optimization of many hundreds parameters of the decoder is carried out. • Problems(Tasks) 1 and 2 - "very difficult" • The problem(task) 3 -coding theory not put at all was V. V. Zolotarev. The 26

Multithreshold decoding (MTD) – MTD repeatedly changes symbols of the accepted message and can achieve at linear complexity of realization the decision of the optimum decoder (OD). – It is a result of the iterative approach application to the error correction. It was revealed at USSR at 22 years earlier, than in the West. – Usually "price" of optimum decoding – (as for Viterbi algorithm, VA) - full search, and complexity MTD - only linear function of a code length!!! V. V. Zolotarev. The coding theory 27 –

What is necessary from codes for communication networks? • Prof. Berlecamp (USA) had said in 1980 in the review : • " It - a code gain! ", - a measure of effect of increase • • • in energy of the signal, estimated as ~ $1 million per 1 d. B CG. Now it is even more important as it is shown on ours website SRI RAS www. mtdbest. iki. rssi. ru Now every additional one d. B CG gives in the big networks economic benefit in hundred millions dollars! Resource CG can be realized for decrease in the sizes of aerials, and also for increase in speed, reliability and distance of communication. It is extremely important for satellite systems of communication such as VSAT, and also projects micro- and nano- satellites or other high-speed systems of communication. V. V. Zolotarev. The coding theory 28

The main fundamental scientific The main transition from analog problem offundamental scientific problem of transition from analog Communications(connections) Communications and computer science to the digital one To digital • Maintenance of a high level • of reliability of formation, Maintenance on completely new processing, transfer and theoretical principles of a high level of storage of figures. • Means of the decision of reliability of transmission and storage of this problem - methods of data. theory of noiseproof coding • The most successful decisions of this problem are offered with theory of noiseproof coding V. V. Zolotarev. The coding theory 29

The main problems of coding technology • 1. To decode - it is easier!. • 2. Reliability - is higher! • 3. Maximum to take into account Conditions of coding in real systems of communication • 4. How it may be reached? Multithreshold Decoders!!! • Why? They are extremely simple and very affective! V. V. Zolotarev. The coding theory 30

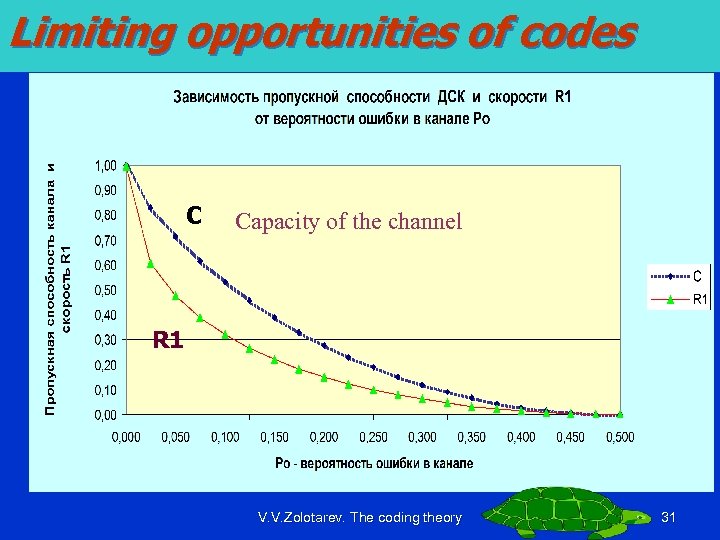Limiting opportunities of codes C Capacity of the channel R 1 V. V. Zolotarev. The coding theory 31

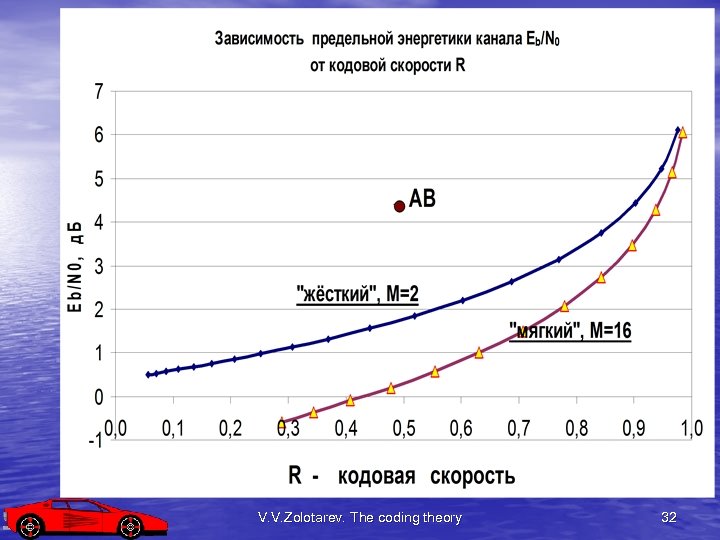V. V. Zolotarev. The coding theory 32

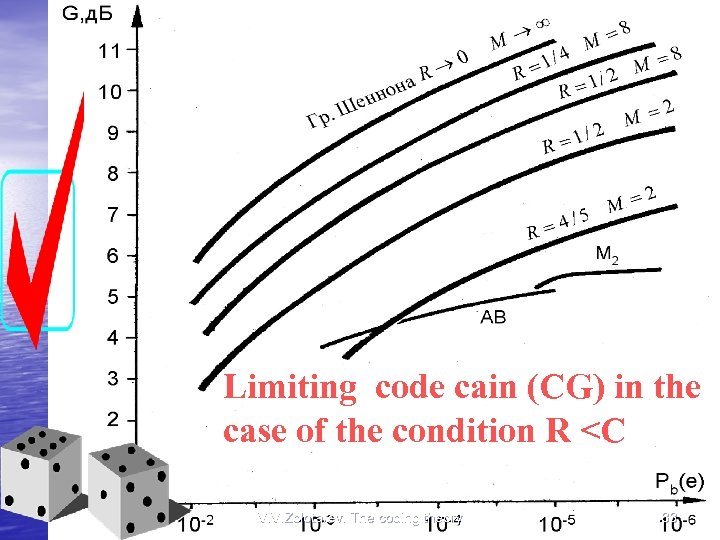Limiting code cain (CG) in the case of the condition R