11d42fb6999aaa2b26627eea117492b7.ppt
- Количество слайдов: 35
 Schwerpunkt Project SPINTRONICS-- 1285 (with J. von Delft LMU Munich QD 2010 Chernogolovka Russia-Israel cooperation IMOST (YG-I. Burmistrov) CHARGE – SPIN INTERPLAY IN QUANTUM DOTS I. Burmistrov, YG, M. Kiselev see also… B. Nissan, YG, M. Kiselev, I. Lerner in progress. . I. Burmistrov, YG, M. Kiselev, L. Medvedovsky – numerics A. Saha, A. Shnirman, A. Altland, YG – geometric phases
Schwerpunkt Project SPINTRONICS-- 1285 (with J. von Delft LMU Munich QD 2010 Chernogolovka Russia-Israel cooperation IMOST (YG-I. Burmistrov) CHARGE – SPIN INTERPLAY IN QUANTUM DOTS I. Burmistrov, YG, M. Kiselev see also… B. Nissan, YG, M. Kiselev, I. Lerner in progress. . I. Burmistrov, YG, M. Kiselev, L. Medvedovsky – numerics A. Saha, A. Shnirman, A. Altland, YG – geometric phases
 what the problem is why is it non-trivial what can we do about it …
what the problem is why is it non-trivial what can we do about it …
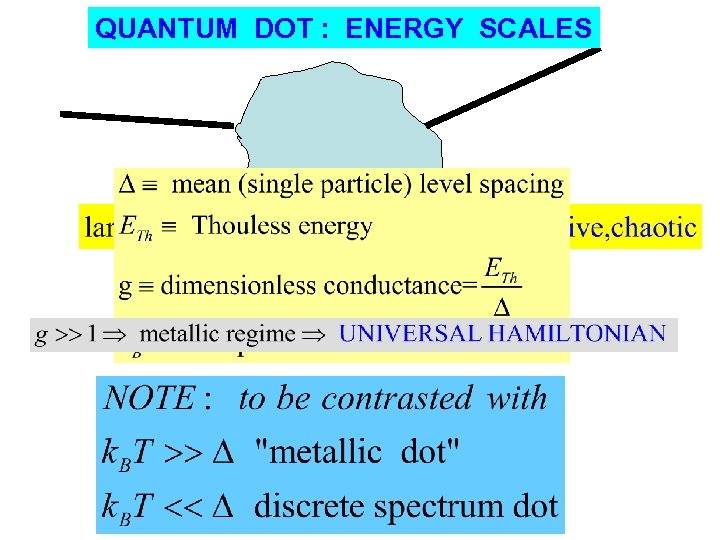 QUANTUM DOT : ENERGY SCALES
QUANTUM DOT : ENERGY SCALES
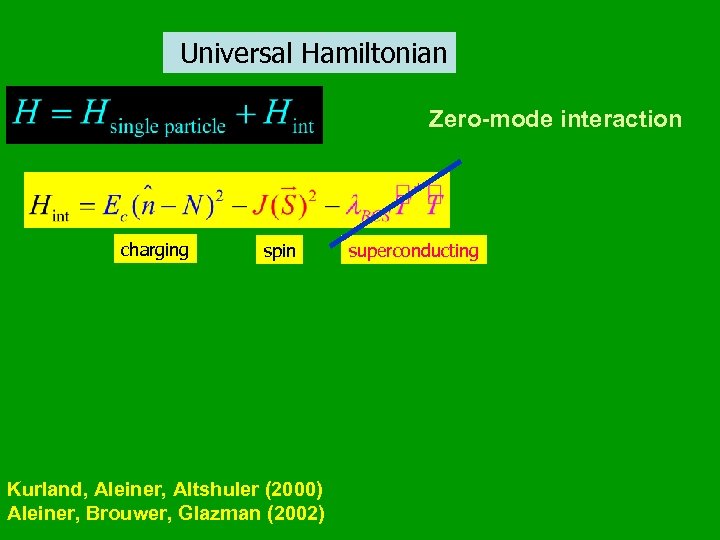 Universal Hamiltonian Zero-mode interaction charging spin Kurland, Aleiner, Altshuler (2000) Aleiner, Brouwer, Glazman (2002) superconducting
Universal Hamiltonian Zero-mode interaction charging spin Kurland, Aleiner, Altshuler (2000) Aleiner, Brouwer, Glazman (2002) superconducting
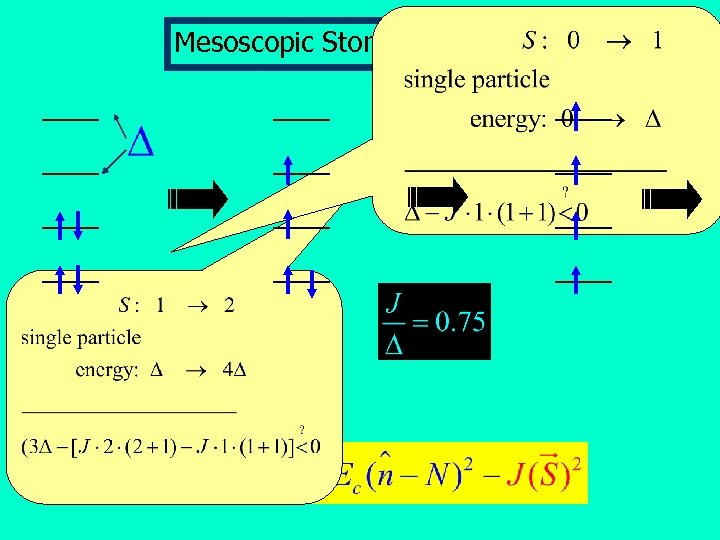 Mesoscopic Stoner Instability
Mesoscopic Stoner Instability
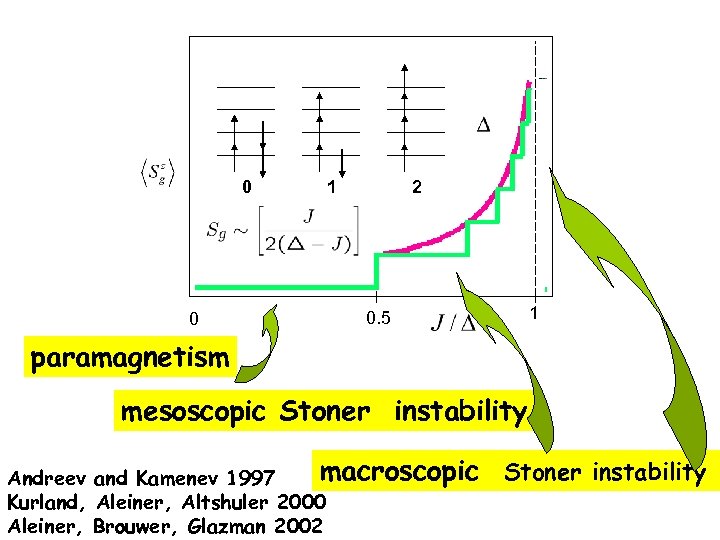 0 0 1 2 1 0. 5 paramagnetism mesoscopic Stoner instability macroscopic Andreev and Kamenev 1997 Kurland, Aleiner, Altshuler 2000 Aleiner, Brouwer, Glazman 2002 Stoner instability
0 0 1 2 1 0. 5 paramagnetism mesoscopic Stoner instability macroscopic Andreev and Kamenev 1997 Kurland, Aleiner, Altshuler 2000 Aleiner, Brouwer, Glazman 2002 Stoner instability
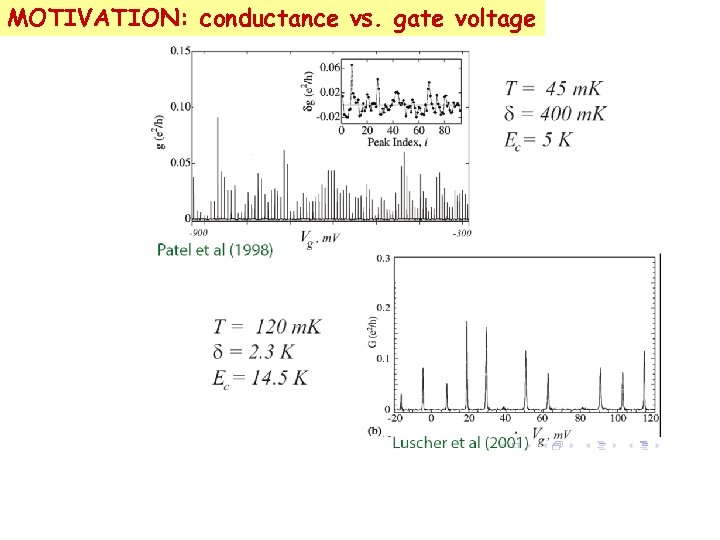 MOTIVATION: conductance vs. gate voltage
MOTIVATION: conductance vs. gate voltage
 MOTIVATION CALCULATE…. TUNNELING DENSITY OF STATES (GF) MAGNETIC SUSCEPTIBILITY (dc, ac) TRANSPORT THROUGH QD …… Alhassid and Rupp, PRL 91, 056801 (2003); Usaj, Baranger, PRB 67, 121308 (2003) Alhassid, Rupp, Kaminski and Glazman PRB 69, 115331(2004); Tureci and Alhassid, PRB 74, 165333 (2006); some aspects --analyzed exactly
MOTIVATION CALCULATE…. TUNNELING DENSITY OF STATES (GF) MAGNETIC SUSCEPTIBILITY (dc, ac) TRANSPORT THROUGH QD …… Alhassid and Rupp, PRL 91, 056801 (2003); Usaj, Baranger, PRB 67, 121308 (2003) Alhassid, Rupp, Kaminski and Glazman PRB 69, 115331(2004); Tureci and Alhassid, PRB 74, 165333 (2006); some aspects --analyzed exactly
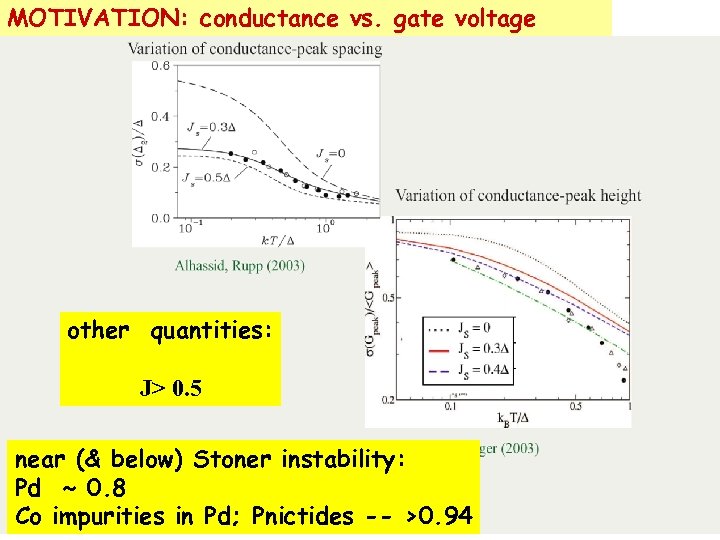 MOTIVATION: conductance vs. gate voltage other quantities: J> 0. 5 near (& below) Stoner instability: Pd ~ 0. 8 Co impurities in Pd; Pnictides -- >0. 94
MOTIVATION: conductance vs. gate voltage other quantities: J> 0. 5 near (& below) Stoner instability: Pd ~ 0. 8 Co impurities in Pd; Pnictides -- >0. 94
 what the problem is why is it non-trivial what can we do about it …
what the problem is why is it non-trivial what can we do about it …
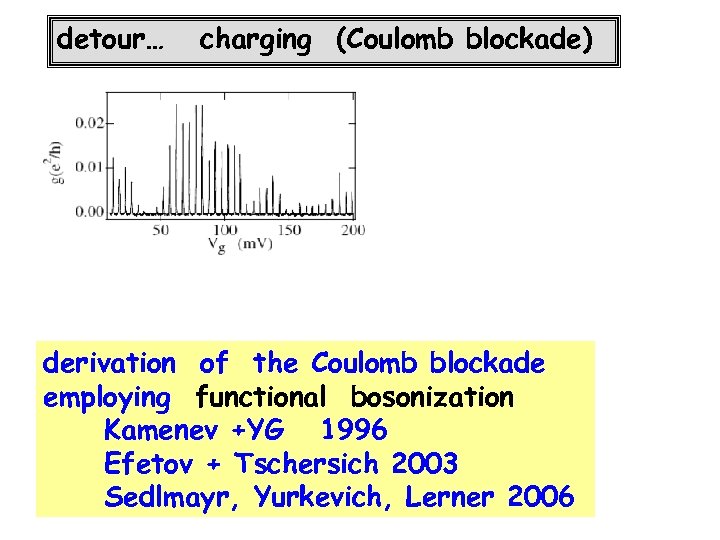 detour… charging (Coulomb blockade) derivation of the Coulomb blockade employing functional bosonization Kamenev +YG 1996 Efetov + Tschersich 2003 Sedlmayr, Yurkevich, Lerner 2006
detour… charging (Coulomb blockade) derivation of the Coulomb blockade employing functional bosonization Kamenev +YG 1996 Efetov + Tschersich 2003 Sedlmayr, Yurkevich, Lerner 2006
 to calculate tunneling density of states needs GF. in imaginary time: Kamenev, YG 1996
to calculate tunneling density of states needs GF. in imaginary time: Kamenev, YG 1996
 interaction term decouple by Hubbard-Stratonovich transformation:
interaction term decouple by Hubbard-Stratonovich transformation:
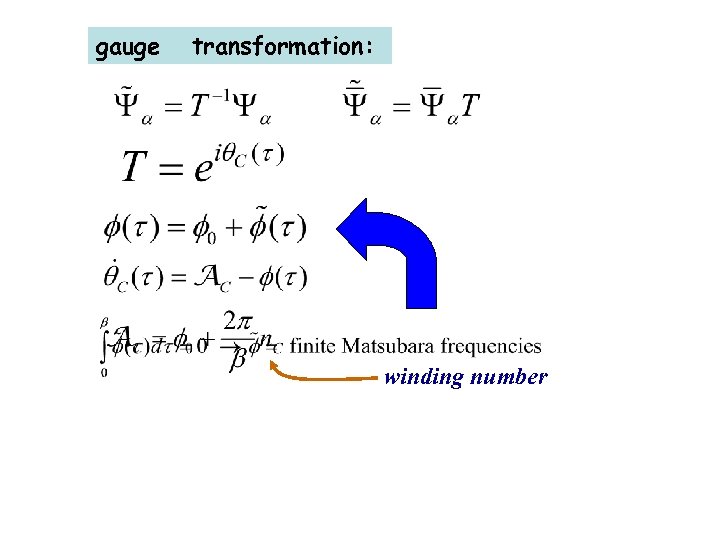 gauge transformation: winding number
gauge transformation: winding number

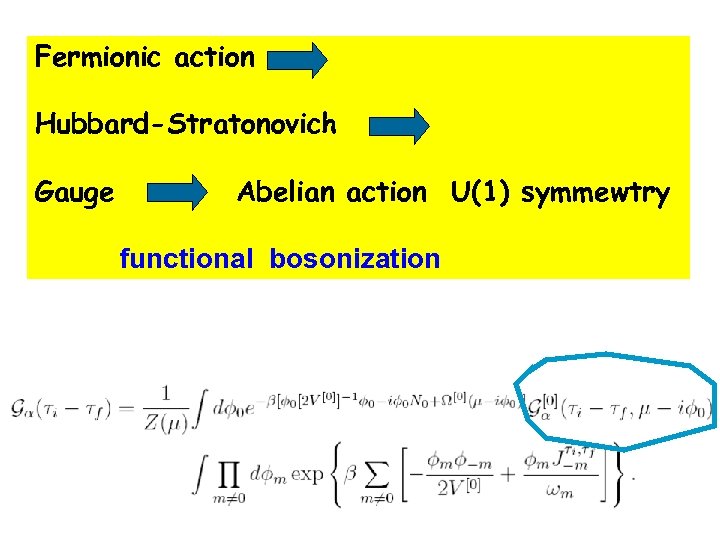 Fermionic action Hubbard-Stratonovich Gauge Abelian action U(1) symmewtry functional bosonization
Fermionic action Hubbard-Stratonovich Gauge Abelian action U(1) symmewtry functional bosonization
 END OF detour… charging (Coulomb blockade) now do the same with spin exchange:
END OF detour… charging (Coulomb blockade) now do the same with spin exchange:
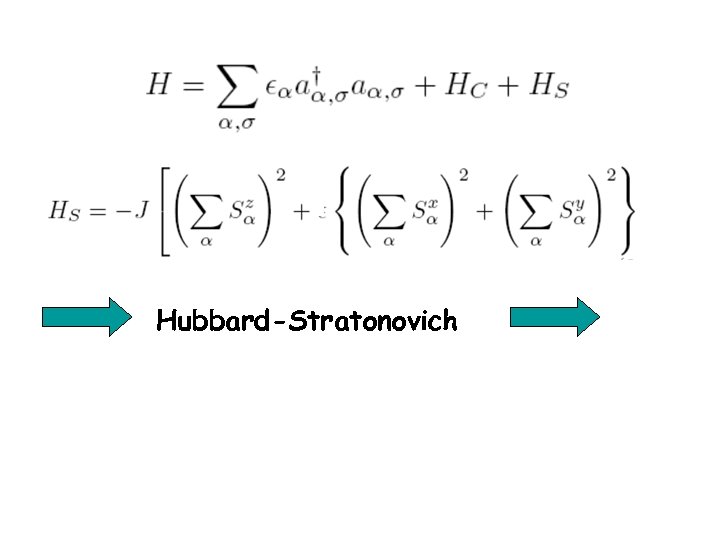 Hubbard-Stratonovich
Hubbard-Stratonovich
 charge+ spin Non-Abelian action ( SU(2) symmetry) various attempts: perturbation in spin anisotropy (Kiselev, YG, 2006) mapping into coupled stochastic eqs. (Kiselev, YG) ? ? ? Ising spin (Nissan, YG, Kiselev, Lerner) Geometric phase (Saha, Shnirman, Altland, Gefen)
charge+ spin Non-Abelian action ( SU(2) symmetry) various attempts: perturbation in spin anisotropy (Kiselev, YG, 2006) mapping into coupled stochastic eqs. (Kiselev, YG) ? ? ? Ising spin (Nissan, YG, Kiselev, Lerner) Geometric phase (Saha, Shnirman, Altland, Gefen)
 what the problem is why is it non-trivial what can we do about it …
what the problem is why is it non-trivial what can we do about it …
 EXACT SOLUTION: action non-Abelian trick: Kolokolov (1990); Wei-Norman (1963)
EXACT SOLUTION: action non-Abelian trick: Kolokolov (1990); Wei-Norman (1963)
 time ordering
time ordering
 EXACT RESULTS Static susceptibility Pauli Curie Stoner inst.
EXACT RESULTS Static susceptibility Pauli Curie Stoner inst.
 EXACT RESULTS canonical partition function without
EXACT RESULTS canonical partition function without
 NON-TRIVIAL CHECKS :
NON-TRIVIAL CHECKS :
 New energy scale emerges : For for crucial dependence on specific realizations; may calculate
New energy scale emerges : For for crucial dependence on specific realizations; may calculate
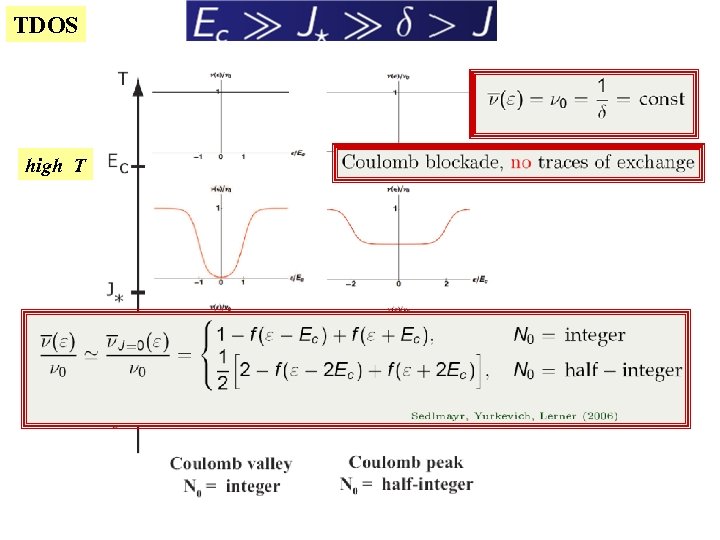 TDOS high T
TDOS high T
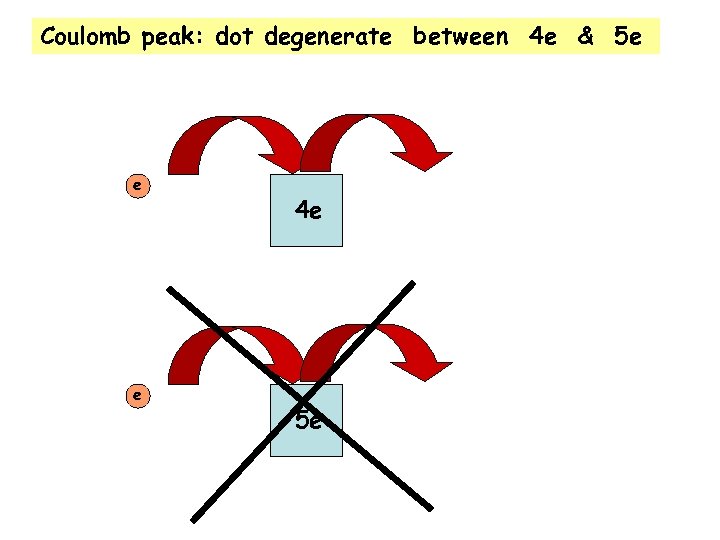 Coulomb peak: dot degenerate between 4 e & 5 e e e 4 e 5 e
Coulomb peak: dot degenerate between 4 e & 5 e e e 4 e 5 e
 TDOS intermediate T exponentially suppressed osc. precession physics
TDOS intermediate T exponentially suppressed osc. precession physics
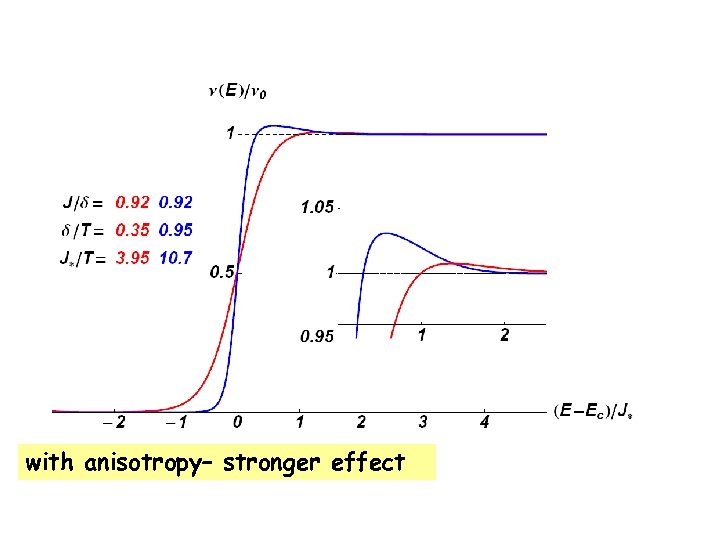 with anisotropy– stronger effect
with anisotropy– stronger effect
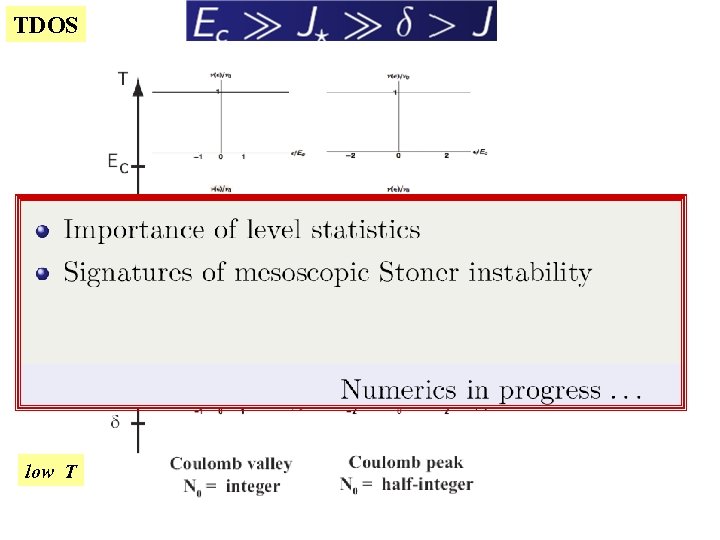 TDOS low T
TDOS low T

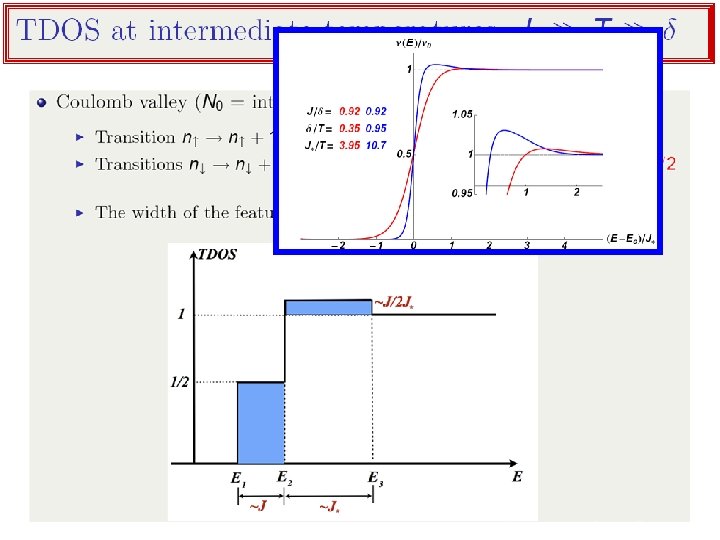
 SUMMARY: exact solution (non-monotonic TDOS; susceptibility; ) Possible Generalizations / Extensions • • anisotropic spin interactions ; finite B; susceptibility (d. c. + a. c. ) include superconductivity channel conductance: sequential tunneling; cotunneling. • disorder
SUMMARY: exact solution (non-monotonic TDOS; susceptibility; ) Possible Generalizations / Extensions • • anisotropic spin interactions ; finite B; susceptibility (d. c. + a. c. ) include superconductivity channel conductance: sequential tunneling; cotunneling. • disorder



