School quality school access and the formation of

School quality, school access and the formation of neighbourhoods Simon Burgess and Tomas Key November 2008 PLUG, Nov 2008 www. bris. ac. uk/CMPO

Motivations • Understanding the role of income in gaining access to good schools. • School access – if proximity matters, how does that come about? Look at differential “strategic” moving rates. • Formation of communities – how segregated communities are formed, in relation to school quality. PLUG, Nov 2008 www. bris. ac. uk/CMPO 2

Results • Estimating the process of moving house in its possible relationship to school quality. • We show that school quality matters. • Strong differences between poor and non-poor families: – For non-poor families there is a relationship between school quality and moving; not so for poor families. • Different process for within- and across-labour market moves. PLUG, Nov 2008 www. bris. ac. uk/CMPO 3

Plan • • • Literature Framework Data Results Conclusions PLUG, Nov 2008 www. bris. ac. uk/CMPO 4

Literature • Results relating house price premia to school quality (Black; Machin & Gibbons). • General equilibrium models of residential location and school selection. – In the US, Epple and Romano; Nechyba; and Bayer and Mc. Millan. – In the UK, a different setting. PLUG, Nov 2008 www. bris. ac. uk/CMPO 5

Framework • Simplified story is: – Families start out w/out children, and choose where to live on that basis – Acquire children and consider relocating before the key date for school assignment – If they choose to move, they attempt to move with increasing effort. – Of course, there are other (random) reasons for moving too. PLUG, Nov 2008 www. bris. ac. uk/CMPO 6

Framework 2 • Assumptions: – In overall equilibrium in the sense that all the distributions of income, tastes, labour market states, amenities and school qualities are fixed. – Within that, individuals move and change within a cohort as it ages. – So house prices are fixed; people move between locations, but in equilibrium, prices remain constant. – School quality and neighbourhood quality are exogenous, unaffected by the people learning or living there (future work …). PLUG, Nov 2008 www. bris. ac. uk/CMPO 7

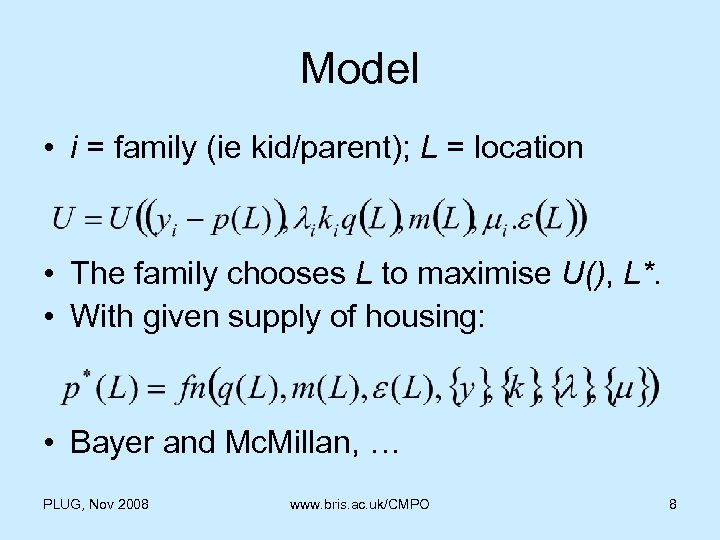Model • i = family (ie kid/parent); L = location • The family chooses L to maximise U(), L*. • With given supply of housing: • Bayer and Mc. Millan, … PLUG, Nov 2008 www. bris. ac. uk/CMPO 8

• Choice of L* with kids or not: • Pick L*(0) to start with at k=0 so q is irrelevant. So necessarily live somewhere nicer in terms of e and/or cheaper. • L* (k=1) cannot be at a lower q than L*(k=0), unless e is correlated in strange way. • The decision whether to move at all or not is balancing the extra cost of higher price Dp, with the value of higher quality, l. Dq. PLUG, Nov 2008 www. bris. ac. uk/CMPO 9

• Invest in attempting to move, c. • So pia = f(c*), and c* = f(a, DUia), where D between k = 0 and k = 1. • Approximate: PLUG, Nov 2008 www. bris. ac. uk/CMPO 10

• So, within TTWA Dm = 0: • Dp* substituted out by Dq, De and location. • Allow for heterogeneity in response to q • Include q or Dq? PLUG, Nov 2008 www. bris. ac. uk/CMPO 11

Data • • • PLASC/NPD 5 censuses merged together Non-selective, non-middle schools LEAs Looked at TTWAs as unit, LEAs. Spatial controls: – TTWA dummies, LEA dummies – LLSOA dummies – Smoothed LLSOA effects from contiguous areas PLUG, Nov 2008 www. bris. ac. uk/CMPO 12

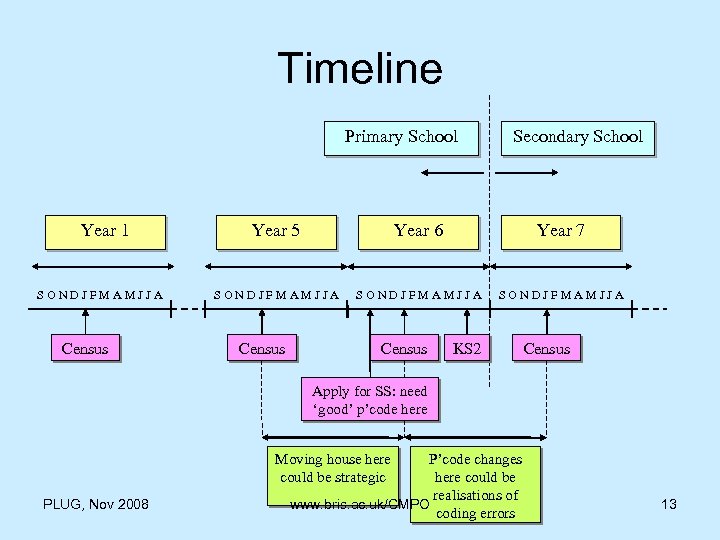Timeline Primary School Year 1 SONDJFMAMJJA Census Secondary School Year 5 Year 6 Year 7 SONDJFMAMJJA Census KS 2 Census Apply for SS: need ‘good’ p’code here P’code changes here could be realisations of www. bris. ac. uk/CMPO coding errors Moving house here could be strategic PLUG, Nov 2008 13

• We have tried several different controls for spatial context: - Dummies for Travel To Work Area - Dummies for Lower Layer Super Output Area (LLSOA) - Smoothed LLSOA effects from contiguous areas, using the IMD Score for neighbouring LLSOAs, as well as the pupil’s own IMD score. • Varying these controls has no qualitative impact on the results. PLUG, Nov 2008 www. bris. ac. uk/CMPO 14

• Two different ways of defining ‘default’ secondary school: – Nearest secondary school – Modal secondary school given primary school attended • Lots of cleaning work on changing postcodes, to eliminate redistricting, input errors and miscoding • We attempt to identify siblings in our data, and pick out eldest mover only. We do this by grouping pupils who move from/to the same postcode, and count these pupils as a family if there are less than 8 of them. PLUG, Nov 2008 www. bris. ac. uk/CMPO 15

Cleaning of p/code changes • We use Royal Mail information about postcode redistricting. • We do not count as moves postcode changes that leave the first and last two characters of the postcode unchanged. • If all in former postcode moved, and all includes more than 8 pupils (our cut-off for a family), then we do not count this as a move: it is likely to have been a redistricting. • We do not count moves of less than 100 m. • We do not count as a move cases where either of the first or last two characters of the postcode only change. • We do not count as a move cases where the first or last two characters only are coded in reverse compared with the postcode for the other academic year. • We do not count as a move cases where there are changes in the postcode length by one character, e. g. AB 1 becoming AB 12 or B 12 becoming CB 12, with all remaining characters unchanged. PLUG, Nov 2008 www. bris. ac. uk/CMPO 16

Results • • • Descriptive analysis of moves Basic analysis of probability of moves Analysis by within- and across-TTWA moves Analysis by pupil age Dynamic, non-linear panel data models with unobserved heterogeneity and initial conditions problems. – Panel analysis 1 – Panel analysis 2 PLUG, Nov 2008 www. bris. ac. uk/CMPO 17

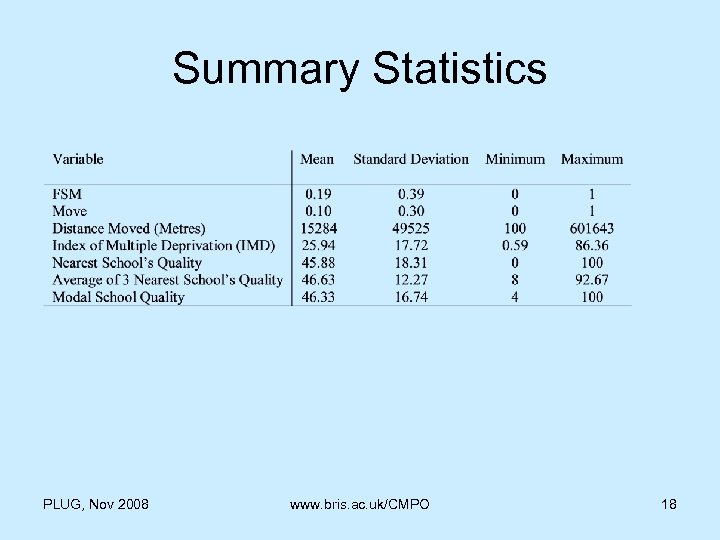Summary Statistics PLUG, Nov 2008 www. bris. ac. uk/CMPO 18

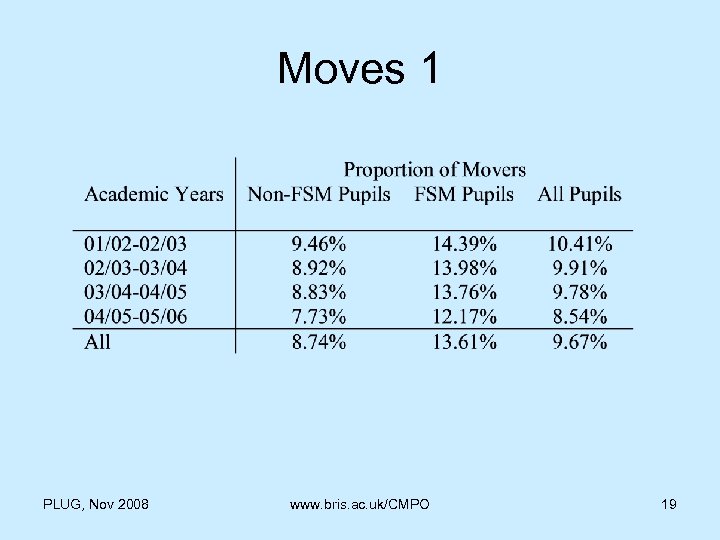Moves 1 PLUG, Nov 2008 www. bris. ac. uk/CMPO 19

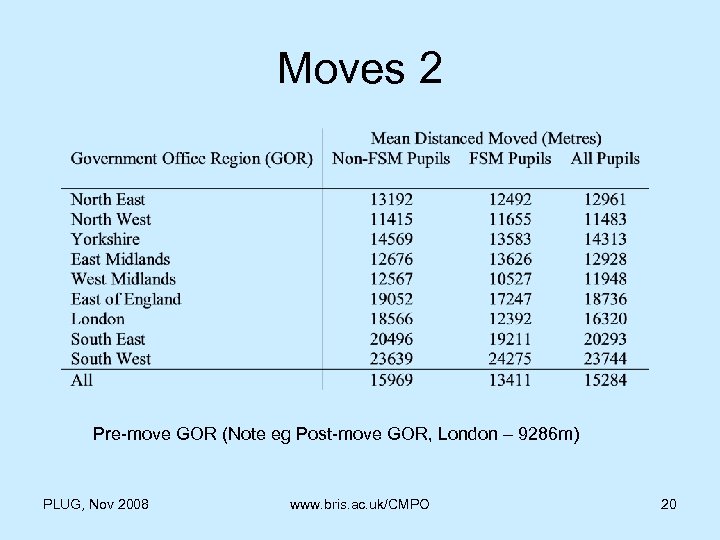Moves 2 Pre-move GOR (Note eg Post-move GOR, London – 9286 m) PLUG, Nov 2008 www. bris. ac. uk/CMPO 20

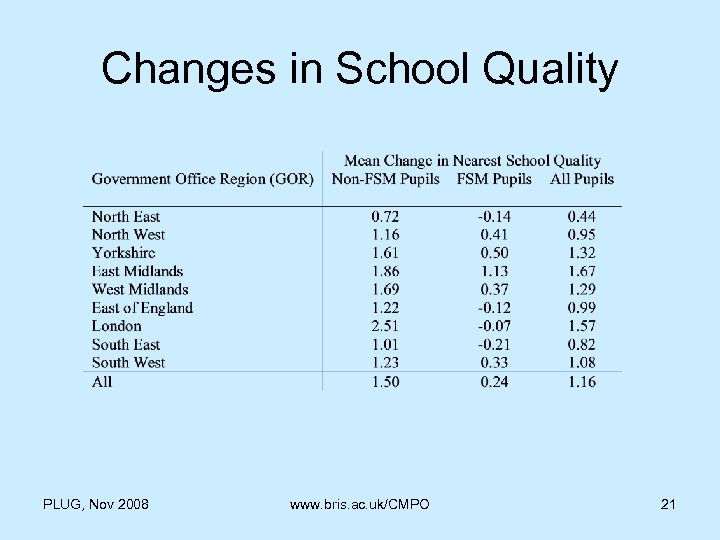Changes in School Quality PLUG, Nov 2008 www. bris. ac. uk/CMPO 21

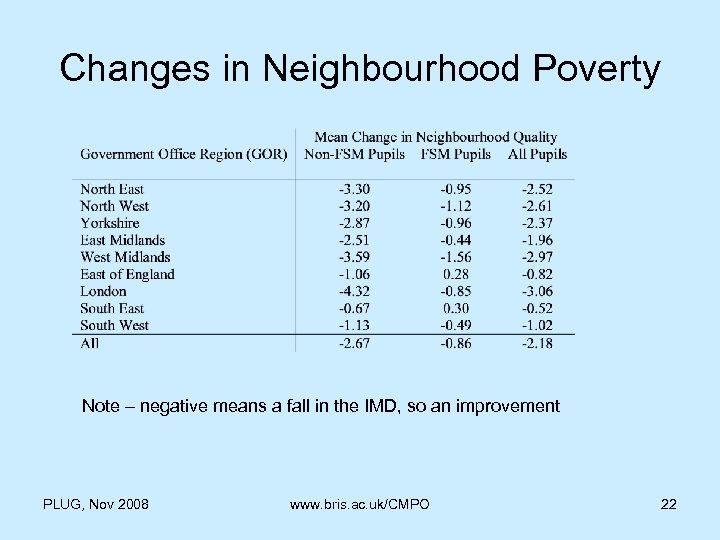Changes in Neighbourhood Poverty Note – negative means a fall in the IMD, so an improvement PLUG, Nov 2008 www. bris. ac. uk/CMPO 22

Basic Results PLUG, Nov 2008 www. bris. ac. uk/CMPO 23

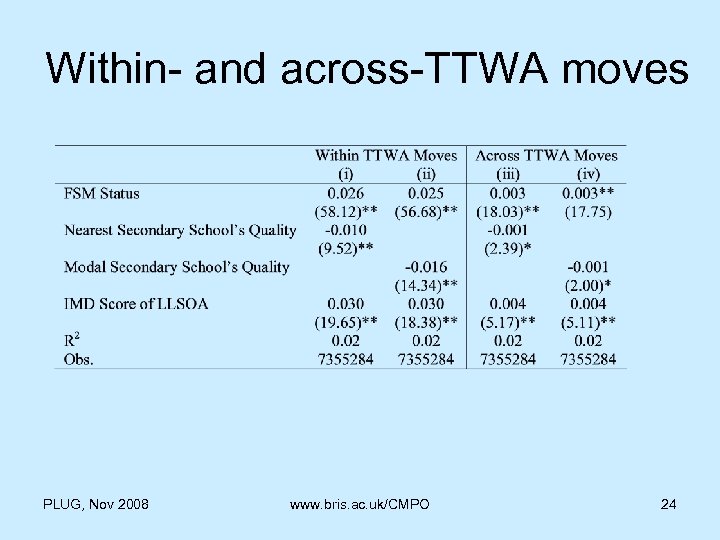Within- and across-TTWA moves PLUG, Nov 2008 www. bris. ac. uk/CMPO 24

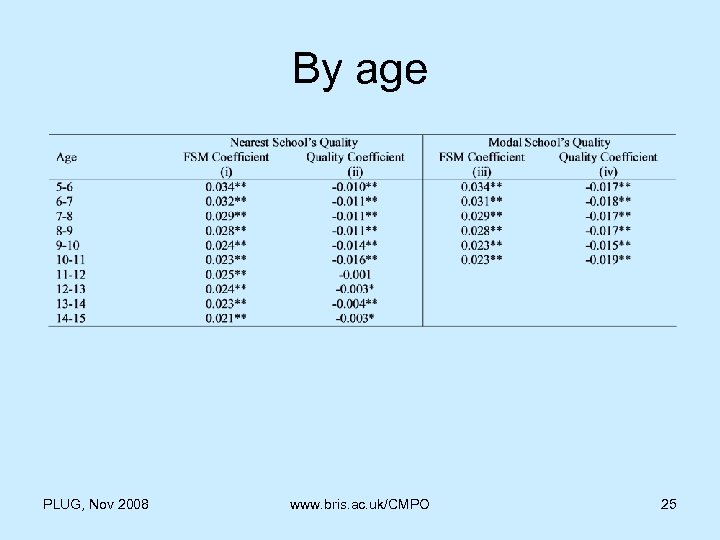By age PLUG, Nov 2008 www. bris. ac. uk/CMPO 25

Econometric Issues • Potential problems: – Omitted variables? Neighbourhood – well covered; schools – GCSE results, other things likely correlated; Families – repeated obs. – Reverse causation? Timing, local controls, movers are small fraction of any school. – Initial conditions problem: current school quality might result from previous choices – a (non-random) group of families may already have moved. PLUG, Nov 2008 www. bris. ac. uk/CMPO 26

Main threat to identification: Birds of paradise behaviour (Some) birds of paradise build a nest first and then seek a mate – not least through having a nice nest to live in. The equivalent here is families moving to get a good default school before having a child to send to the school. If pre-kid location chosen independent of school quality, then in principle this is ok as an initial condition. Separate practical problem that we don’t see everyone from the start. PLUG, Nov 2008 www. bris. ac. uk/CMPO 27

Econometric Issues • Assume q (age = 0) is exogenous, we first see people at age = A. Some movers may already have moved by then. • Who would move early? People with high preference for schooling, low preference for other amenities • So expect a bigger coefficient if capture more and earlier part of families’ lives. Confirmed: get bigger coefficient on short early window, and on long window. PLUG, Nov 2008 www. bris. ac. uk/CMPO 28

Panel Analysis • Use Wooldridge’s approach for dynamic nonlinear models with unobserved effects and initial conditions problems. • Approach models the distribution of the unobserved heterogeneity conditional on the initial value. • Essentially a random effects probit model with controls for initial state. PLUG, Nov 2008 www. bris. ac. uk/CMPO 29

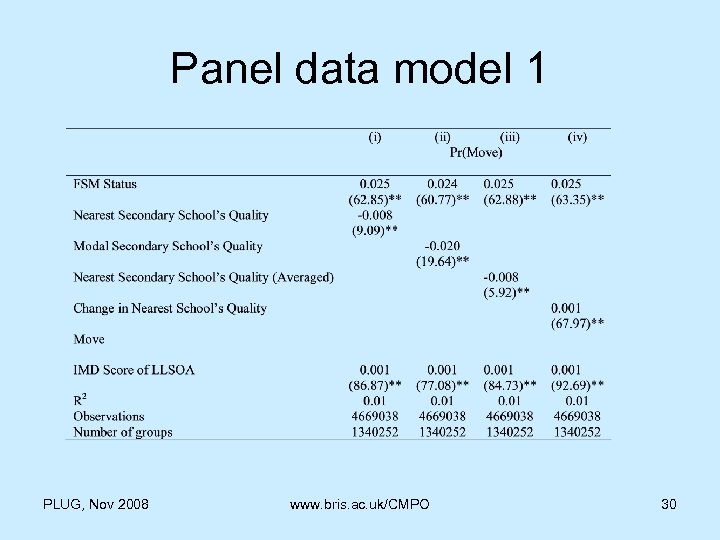Panel data model 1 PLUG, Nov 2008 www. bris. ac. uk/CMPO 30

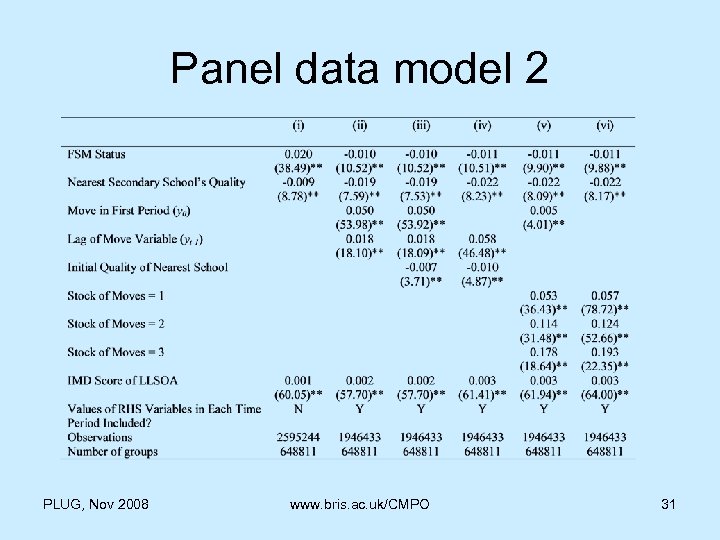Panel data model 2 PLUG, Nov 2008 www. bris. ac. uk/CMPO 31

Conclusions • Implications for school access. • Implications for the formation of neighbourhoods. – Invert estimated moving model to analyse the composition of neighbourhoods. • Future work: … joint model of school performance and neighbourhood formation PLUG, Nov 2008 www. bris. ac. uk/CMPO 32