SCF-техники Използване на симетрията Двуелектронни интеграли Изисквания

SCF-техники Използване на симетрията Двуелектронни интеграли

Изисквания за SCF-сходимост Основна ключова дума: # SCF RHF 3 -21 G*. . . Информация в изходния файл: Requested convergence on RMS density matrix = 1. 00 D-04 within. . . cycles. Requested convergence on MAX density matrix = 1. 00 D-02 Requested convergence on energy = 5. 00 D-05 При успех: . . . SCF Done: E(RHF) = -226. 517764737 Convg = 0. 9093 D-04 A. U. after При неуспех: . . . Restarting incremental Fock formation. >>>>> Convergence criterion not met. . . Convergence failure -- run terminated. Error termination via Lnk 1 e in /usr/g 98/l 502. exe. 6 cycles

Стандартни стойности на SCF-критерии Gaussian #SCF=Single. Point(SP, Sleazy) 10 -4/10 -2/10 -5 a. u. . . По подразбиране при 1 SCF HF/DFT изчисления #SCF=Tight 10 -8/10 -6 a. u. . . По подразбиране при останалите изчисления #SCF(Conver=7) 10 -7/10 -5 a. u. . . Според спецификата на задачата Hyperchem 10 -2 kcal/mol за енергията при ММ и полуемпирични методи 10 -8 kcal/mol за енергията при ab initio и DFT методи H. B. Schlegel and J. J. Mc. Douall, in Computational Advances in Organic Chemistry, Ed. C. Ogretir and I. G. Csizmadia (Kluwer Academic, The Netherlands, 1991) 167 -185

Проблемите. . . Кога възникват? ~ твърде напрегната геометрия – преходни състояния, линейни молекули ~ големи базиси съдържащи дифузни функции ~ молекули с изродени или близколежащи (спинови) състояния – радикали, съединения на преходни метали ~ високосиметрични структури – нанотръби, фулерени ~ неподходящи изходни молекулни орбитали “Работна” молекула: RHF/3 -21 G* Симетрия: Cs оцетна к-на

Решението. . . Рестартиране на SCF-процедурата Изчислението продължава от последния етап записан в предварително зададен checkpoint файл. Препоръчва се само при технически проблеми, напр. спиране на тока или “намеса” на външни лица. %chk=acet_restart #SCF=Restart RHF 3 -21 G*. . . SCF restart from the checkpoint file: acet_restart. chk Увеличаване броя на SCF-циклите Предвидени са по подразбиране 64 (G 03) и съответно 50 (НС) цикъла за достигане на сходимост. Само увеличаването им рядко помага за решаване на проблема. #SCF(Max. Cycle=200) RHF 3 -21 G*. . . Requested convergence. . . within 200 cycles. . . SCF Done: E(RHF) = after 1 cycles . . .

Решението. . . Екстраполация (extrapolation)# Текущата матрица на плътността се екстраполира от няколко (най-често 3) предишни Най-разпространен вариант – директна инверсия в подпространството на итерациите (DIIS) минимизира се функция на грешката #SCF=DIIS RHF 3 -21 G*. . . Job cpu time: 0 days 0 hours По подразбиране в G 03. Няма специално съобщение. 0 minutes 7. 0 seconds. # Методът може да се прилага само при геометрична оптимизация.

Решението. . . Нагнетяване (damping)# В текущата матрица на плътността се включва част от предишната с някакво тегло = const #SCF=Damp RHF 3 -21 G*. . . Job cpu time: 0 days 0 hours Няма специално съобщение. 0 minutes 13. 0 seconds. const – варира се през първите N цикъла #SCF(Ndamp=10) RHF 3 -21 G*. . . Job cpu time: 0 days 0 hours Няма специално съобщение. 0 minutes 7. 0 seconds. # Методът може да се прилага само при геометрична оптимизация.

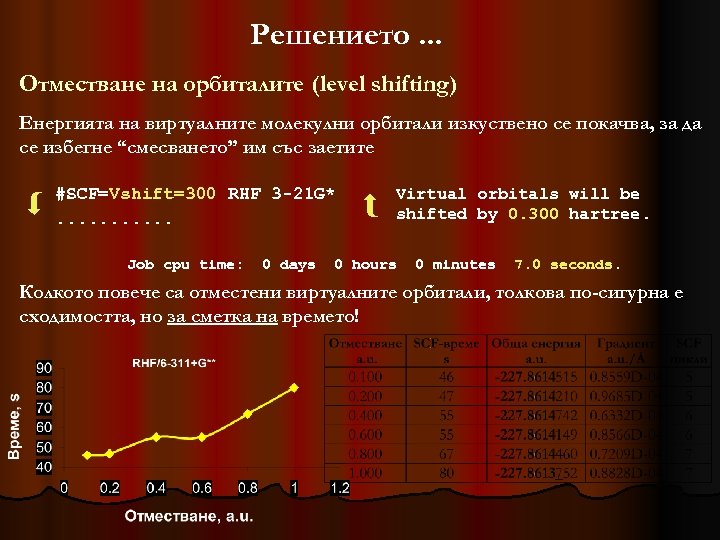Решението. . . Отместване на орбиталите (level shifting) Енергията на виртуалните молекулни орбитали изкуствено се покачва, за да се избегне “смесването” им със заетите #SCF=Vshift=300 RHF 3 -21 G*. . . Job cpu time: 0 days Virtual orbitals will be shifted by 0. 300 hartree. 0 hours 0 minutes 7. 0 seconds. Колкото повече са отместени виртуалните орбитали, толкова по-сигурна е сходимостта, но за сметка на времето!

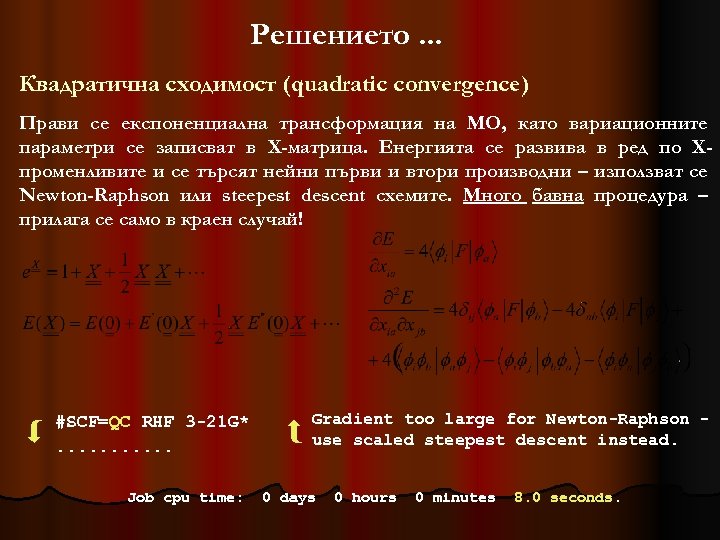Решението. . . Квадратична сходимост (quadratic convergence) Прави се експоненциална трансформация на МО, като вариационните параметри се записват в Х-матрица. Енергията се развива в ред по Хпроменливите и се търсят нейни първи и втори производни – използват се Newton-Raphson или steepest descent схемите. Много бавна процедура – прилага се само в краен случай! #SCF=QC RHF 3 -21 G*. . . Job cpu time: Gradient too large for Newton-Raphson use scaled steepest descent instead. 0 days 0 hours 0 minutes 8. 0 seconds.

Използване на симетрията Интегралите имат ненулева стойност, само когато функциите принадлежат към едно и също неприводимо представяне. При използване на симетрията: ü намалява се количеството на входните данни; ü матричните представяния на операторите стават блок-диагонални; ü отпада съществена част от интегралите; ü изчислителното време намалява симетричните операции в групата. толкова пъти, колкото са Възможно е да се получи решение с по-висока енергия от истинкото!

Симетрична информация Основна ключова дума: # Symm scf=Focksymm RHF 3 -21 G*. . . Молекулната симетрия се задава чрез Z-матрицата (G 03) или при конструиране на модела (HC). . . Ethylene (D 2 h) Geometry Optimization 0 C C H H 1 1 2 2 CC CH 2 HCC 3 180. CH 1 HCC 4 180. Variables: CC=1. 31 CH=1. 07 HCC=121. 5. . .

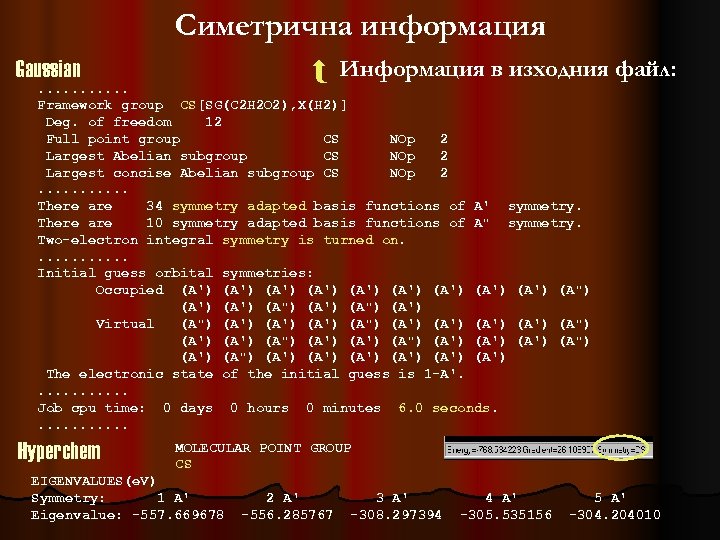Gaussian Симетрична информация Информация в изходния файл: . . . Framework group CS[SG(C 2 H 2 O 2), X(H 2)] Deg. of freedom 12 Full point group CS NOp 2 Largest Abelian subgroup CS NOp 2 Largest concise Abelian subgroup CS NOp 2. . . There are 34 symmetry adapted basis functions of A' symmetry. There are 10 symmetry adapted basis functions of A" symmetry. Two-electron integral symmetry is turned on. . . Initial guess orbital symmetries: Occupied (A') (A') (A') (A") (A') Virtual (A") (A') (A') (A") (A') (A') (A") (A') (A') The electronic state of the initial guess is 1 -A'. . . Job cpu time: 0 days 0 hours 0 minutes 6. 0 seconds. . . Hyperchem MOLECULAR POINT GROUP CS EIGENVALUES(e. V) Symmetry: 1 A' Eigenvalue: -557. 669678 2 A' -556. 285767 3 A' -308. 297394 4 A' -305. 535156 5 A' -304. 204010

Понижаване или премахване на симетрията Задаване на занижени критерии при определяне на първоначалната симетрия – при неоптимална или експериментална входна геометрия #Symm=Loose RHF 3 -21 G*. . . Няма специално съобщение. Не се разрешава използване на симетрията при самосъгласуване на МО – доста времеемко при големи задачи #Symm=No. SCF RHF 3 -21 G*. . . #SCF=No. Symm RHF 3 -21 G*. . . SCF N**3 symmetry information disabled. Не се използва симетрията при пресмятане на двуелектронните интеграли #Symm=No. Int RHF 3 -21 G*. . . #Int=No. Symm RHF 3 -21 G*. . . Two-electron integral symmetry is turned off.

Пресмятане на двуелектронни интеграли Броят на двуелектронните интеграли е ~ M 4/8 възникват проблеми с дисковото пространство и паметта Методи за изчисляване на двуелектронни интеграли: Конвенционален (conventional) Интегралите се изчисляват в началото и се съхраняват на диска, като при всяка итерация се прочитат и презаписват. По подразбиране в НС. Предимства: ü Изисква сравнително малко памет #SCF=Conventional RHF 3 -21 G*. . . Job cpu time: Недостатъци: N Четенето е бавна операция N Необходимо е огромно дисково пространство при повече от 150 базисни функции! Out 2 e will use a cutoff of 1. 00 D-10 265066 integrals produced for a total of 265066. Phoenix requires 263168 words of memory. 0 days 0 hours 0 minutes 14. 0 seconds.

Пресмятане на двуелектронни интеграли В паметта (In. Core) RAM = 500 000 W +M 4/8 (RHF); 500 000 W +M 4/4 (UHF); Интегралите се изчисляват и се съхраняват в паметта. Предимства: Недостатъци: ü Изключително бърза процедура! N Необходимо е огромно количество RAM дори и за малки задачи! #SCF=In. Core RHF 3 -21 G*. . . Keep R 1 integrals in memory in canonical form, NReq=959022. Job cpu time: 0 days 0 hours 0 minutes 6. 0 seconds. Директен (Direct) Интегралите се преизчисляват всеки път при необходимост. По подразбиране в G 03 Предимства: ü Бърз за големи задачи ü Оптимални памет и диск #SCF=Direct. . . RHF 3 -21 G* Job cpu time: Недостатъци: N Бавен за малки задачи, трябва да се знае пресечната точка Няма 0 days специално съобщение. 0 hours 0 minutes 7. 0 seconds.

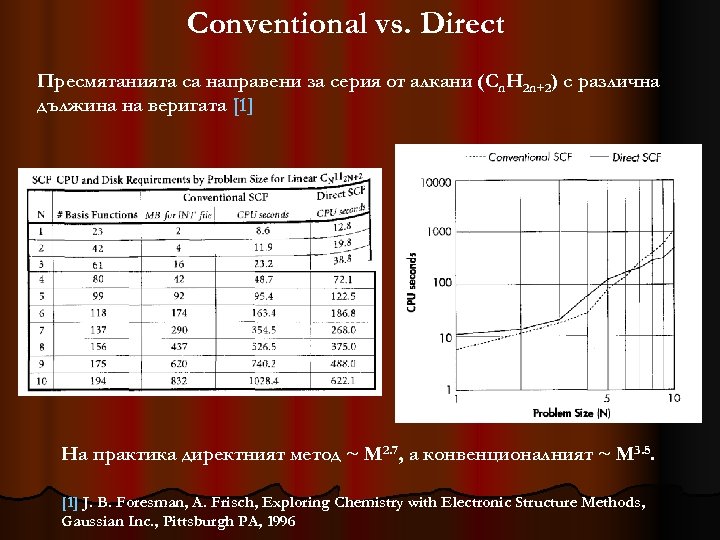Conventional vs. Direct Пресмятанията са направени за серия от алкани (Cn. H 2 n+2) с различна дължина на веригата [1] На практика директният метод ~ M 2. 7, а конвенционалният ~ M 3. 5. [1] J. B. Foresman, A. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian Inc. , Pittsburgh PA, 1996

Формат на двуелектронните интеграли Основна ключова дума: # Int RHF 3 -21 G*. . . Интегралите могат да бъдат в Raffenetti или обикновен (regular) формат. Raffenetti формат #Int=Raff RHF. . . 3 -21 G* Raffenetti 1 integral format. Част от интегралите могат да се съхраняват на диска. #Int=Pass RHF. . . 3 -21 G* Няма специално съобщение.

Ускоряване на процедурите Отсяване на интегралите (integral screening) на партиди – неравенство на Шварц. Формиране на Фоковата матрица по части (incremental Fock formation) – пресмятат се само тези интеграли, които са се променили спрямо предишната итерация. По подразбиране в G 03. #SCF=Inc. Fock. . . RHF 3 -21 G* Няма специално съобщение. Тази техника може да сведе скалирането при изчисляване на двуелектронните интеграли най-много до ~ M 2.

Ускоряване на процедурите Бързи мултиполни моменти (Fast Multipole Moments) – линейно скалиране с M. Близкодействащата част се смята точно, а далекодействащата – като взаимодействие между мултиполи разположени в центъра на всяка клетка. #FMM RHF 3 -21 G*. . . Job cpu time: Няма 0 days специално съобщение. 0 hours 0 minutes 8. 0 seconds. Работи добре за достатъчно големи задачи (> 60 атома)! Ефективен е най-вече за кулоновите, но не и за обменните интеграли! А сега опитайте сами. . .