Scattering and diffraction Based on chapert 4

$Scattering and diffraction Based on chapert 4 + some crystallography$

Scattering and diffraction Based on chapert 4 + some crystallography

Repetition and continuation The probability of scattering is described in terms of either an “interaction cross-section” (σ) or a mean free path (λ). Differential scattering cross section (dσ/dΩ). i. e. the probability for scattering in a solid angle dΩ 100 ke. V: σelastic = ~10 -22 m 2 σinelastic = ~10 -22 - 10 -26 m 2 Is almost always the dominant compo of the total scattering.

Scattering • Elastic Electron-nucleon High angle scattering Rutherford scattering Electron-electron Low angle scattering • Inelastic Electron-nucleon Bremsstrahlung Electron-electron X-rays SE Plasmons Electron-atoms Phonons

Inelastic scattering electron-nucleus interaction • Kramers cross section – To predict bremsstrahlung production N(E)=KZ(E 0 – E)/E, N(E): number of bremsstrahlung photons, K: konstant E<~2 ke. V is absorbed in the specimen and detector

Ineleastic scattering electron-electron interaction σ (m 2) 10 -21 Cross sections in Al assuming θ~0 o P E L 10 -23 K 10 -25 SE 100 200 300 Incident beam energy (ke. V) 400

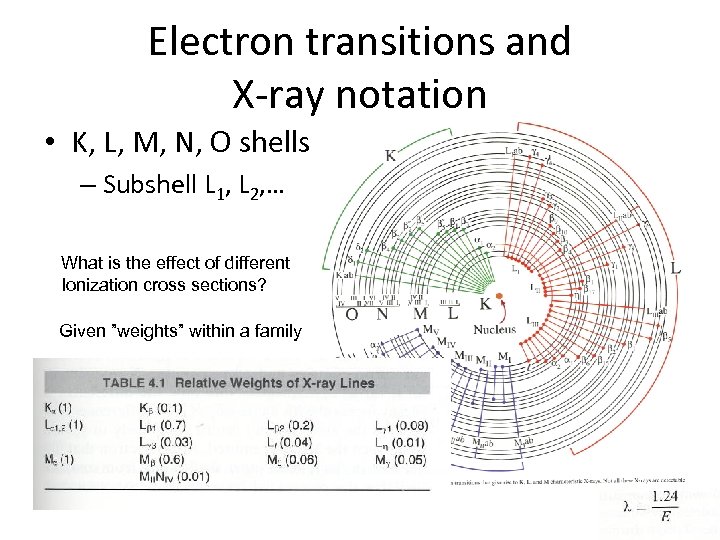
Electron transitions and X-ray notation • K, L, M, N, O shells – Subshell L 1, L 2, … What is the effect of different Ionization cross sections? Given ”weights” within a family

Inelastic scattering → Ionization Total ionization cross section (Bethe -1930): ns: number of electrons in the ionized subshell bs and cs: constants for that shell Ec: Critical ionization energy -Shell and Z dependent (Measured by EELS) - The differential form show that the scattered electron deviate through very small angles (<~10 mrad). -The resultant characteristic X-ray is a spherical wave emitted uniformly over 4π sr -with relativistic correction (Williams -1933): Relativistic factor β=v/c

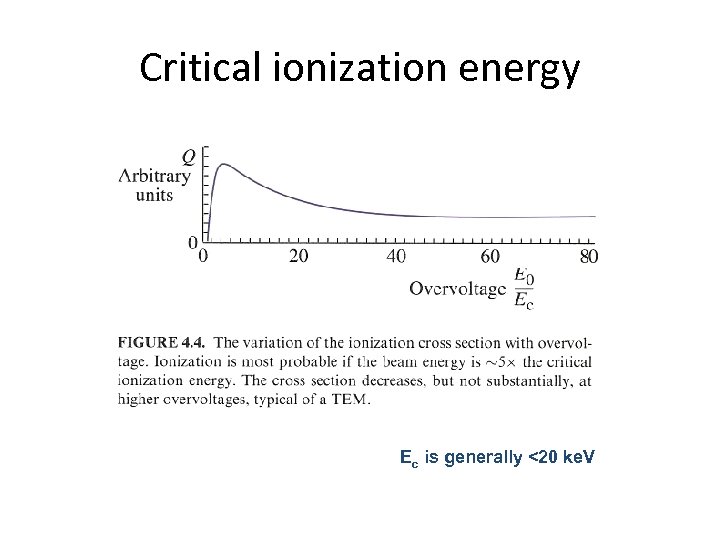
Critical ionization energy Ec is generally <20 ke. V

Difference between Ec and the X-ray energy

Cascade to ground • An ionized atom returns to ground state via a cascade of transitions.

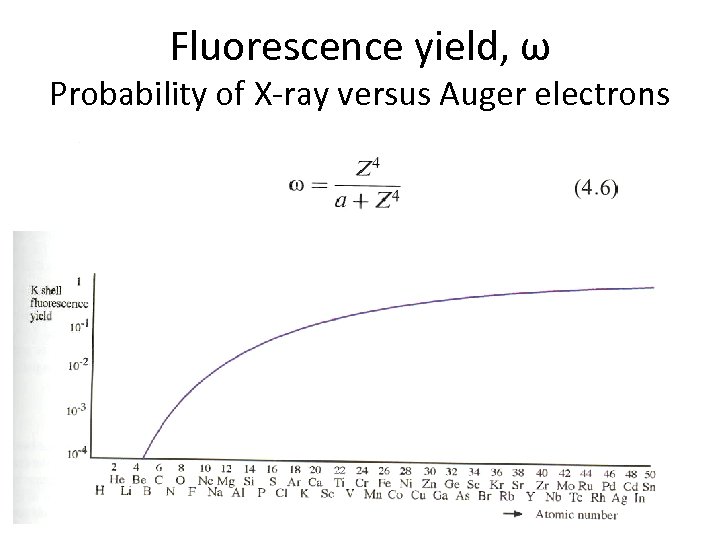
Fluorescence yield, ω Probability of X-ray versus Auger electrons

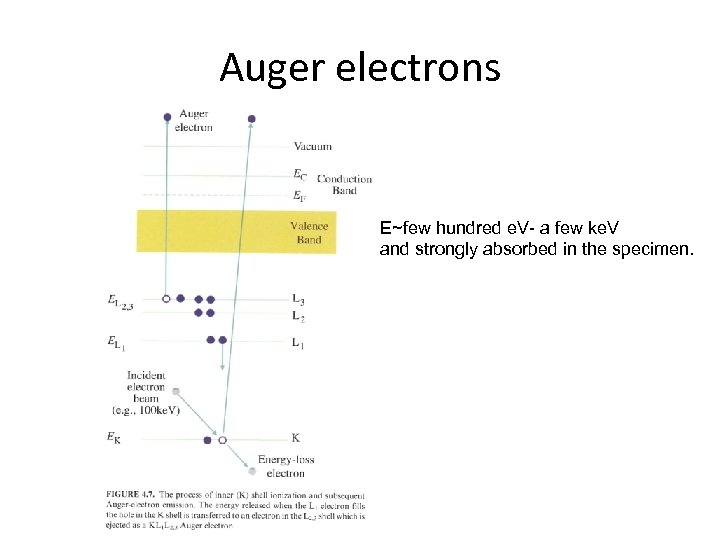
Auger electrons E~few hundred e. V- a few ke. V and strongly absorbed in the specimen.

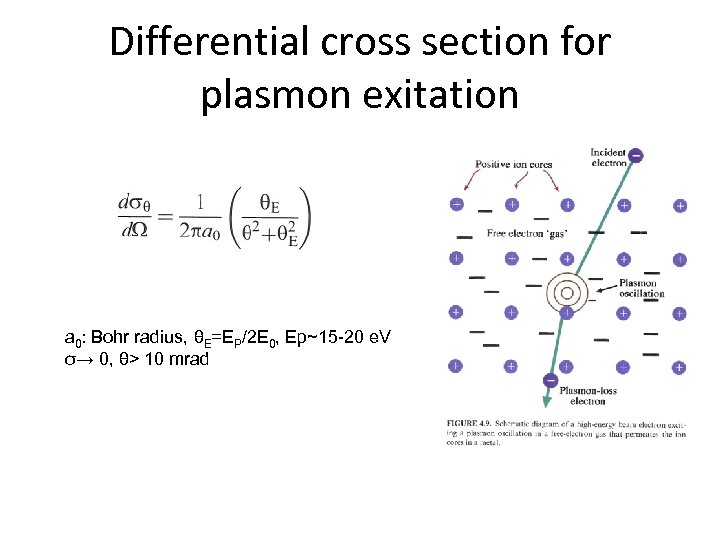
Differential cross section for plasmon exitation a 0: Bohr radius, θE=EP/2 E 0, Ep~15 -20 e. V σ→ 0, θ> 10 mrad

Phonon scattering • Scatter electrons to 5 - 15 mrad – Diffuse background in diffraction pattern – Energy loss < 0. 1 e. V – Scattering increases with Z (~ Z 3/2)

Beam damage • Three principal forms Effect of HT? – Radiolysis • Inelastic scattering breaks chemical bonds – Knock-on damage or sputtering • Displacement of atoms from the crystal lattice → point defects – Heating • Source of damage to polymers and biological tissue. Electron dose : Charge density (C/m 2) hitting the specimen

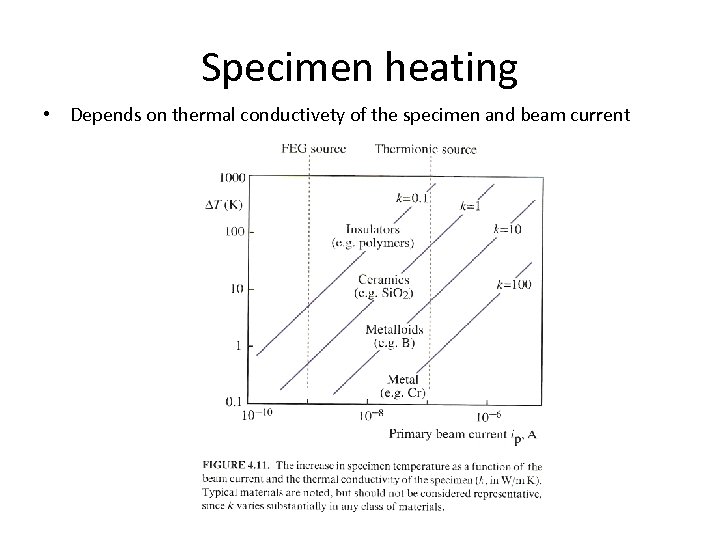
Specimen heating • Depends on thermal conductivety of the specimen and beam current

Knock-on damage • Directly related to the incident beam energy – Primary way metals are damaged • Frenkel pair – Bond strength is a factor • Related to the displacement energy Threshold energy for dispacement of an atoms with atomic weight A:

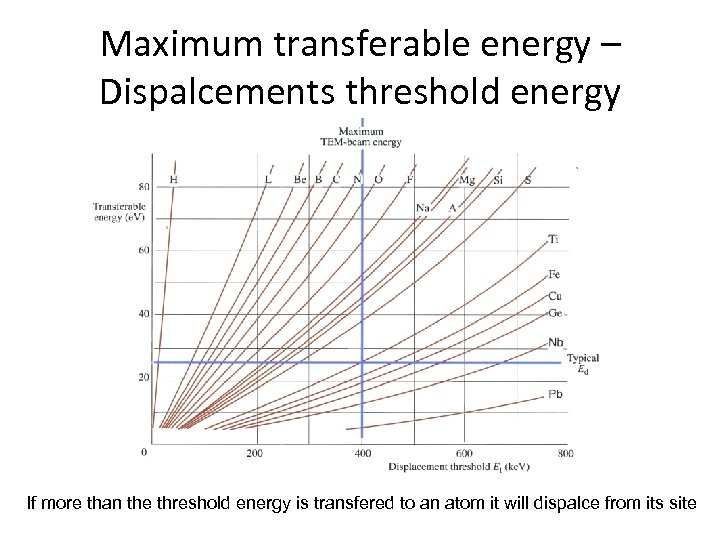
Maximum transferable energy – Dispalcements threshold energy If more than the threshold energy is transfered to an atom it will dispalce from its site

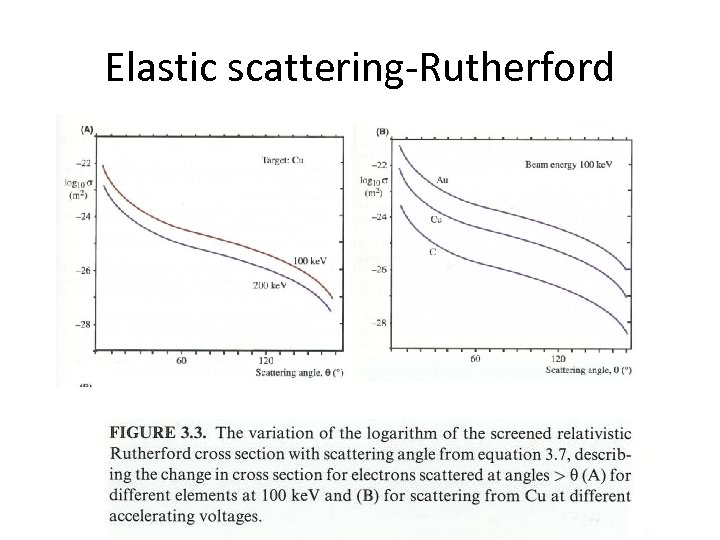
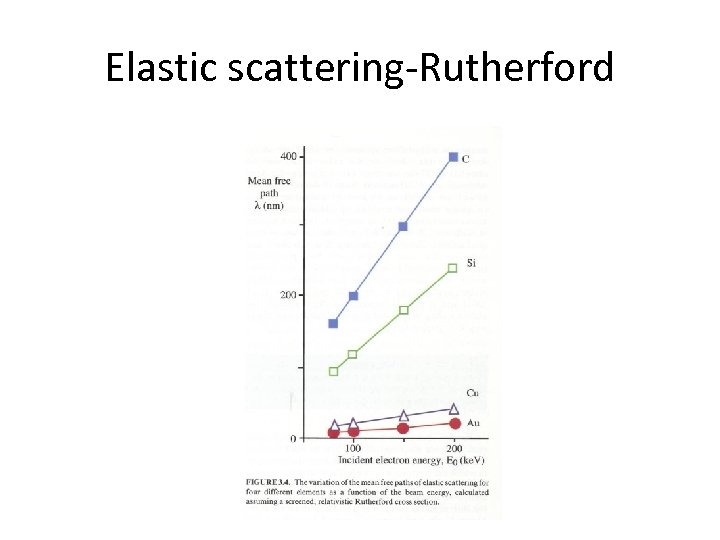
Elastic scattering-Rutherford

Elastic scattering- small angles (<~3 o) • Rutherford cross section can not be used • Scattering-factor approach is complementary – Wave nature of electrons Amplitudes: – Atomic scattering factor f(θ) – Structure factor F(θ)

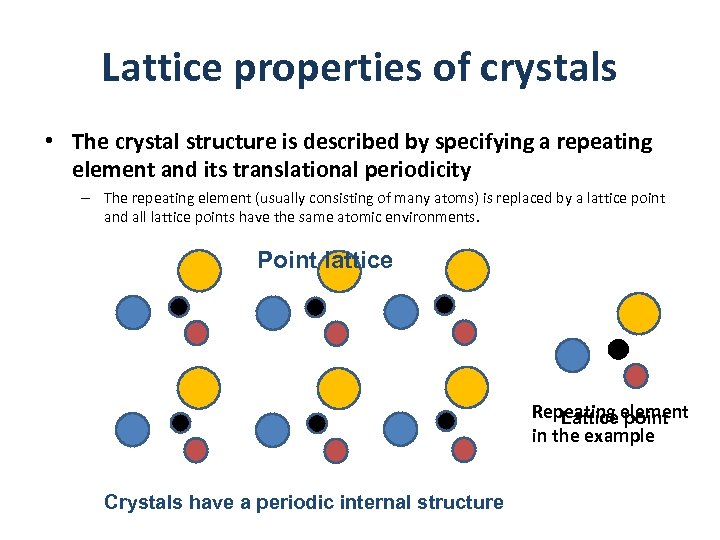
Lattice properties of crystals • The crystal structure is described by specifying a repeating element and its translational periodicity – The repeating element (usually consisting of many atoms) is replaced by a lattice point and all lattice points have the same atomic environments. Point lattice Repeating element Lattice point in the example Crystals have a periodic internal structure

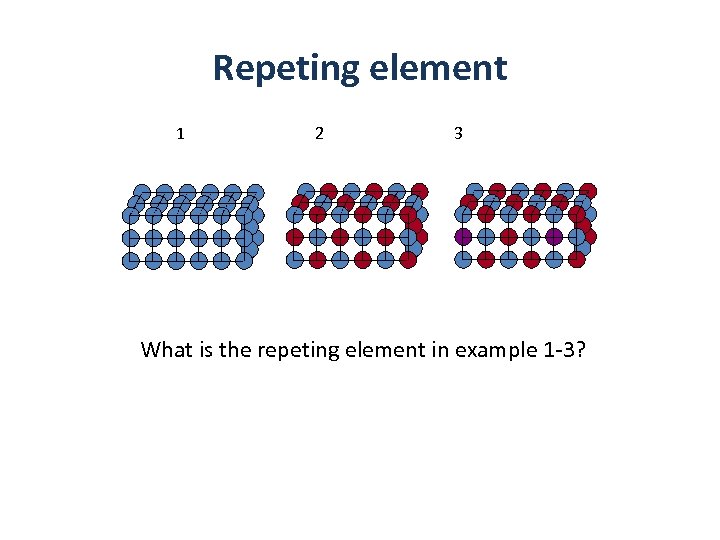
Repeting element 1 2 3 What is the repeting element in example 1 -3?

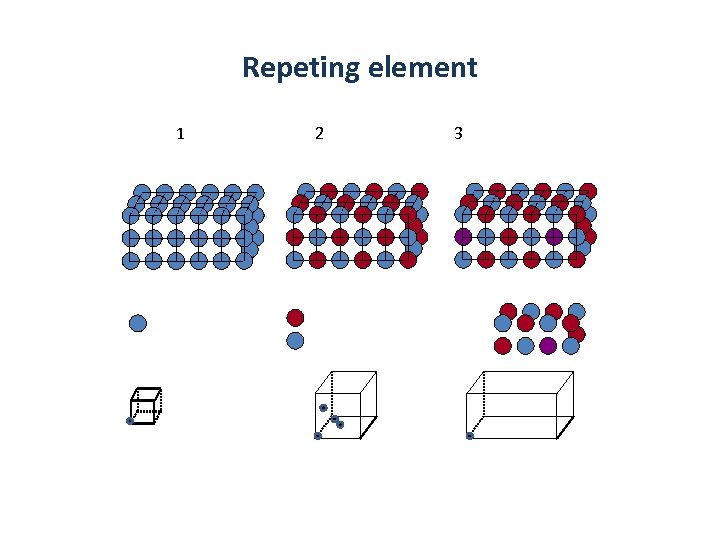
Repeting element 1 2 3

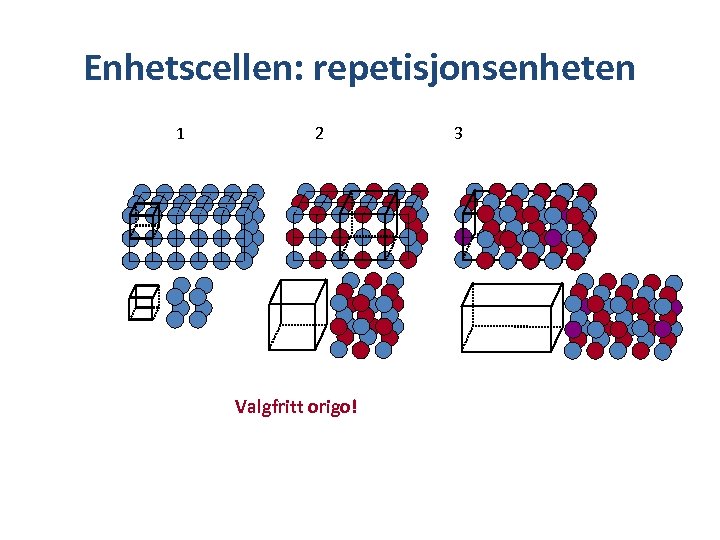
Enhetscellen: repetisjonsenheten 1 2 Valgfritt origo! 3

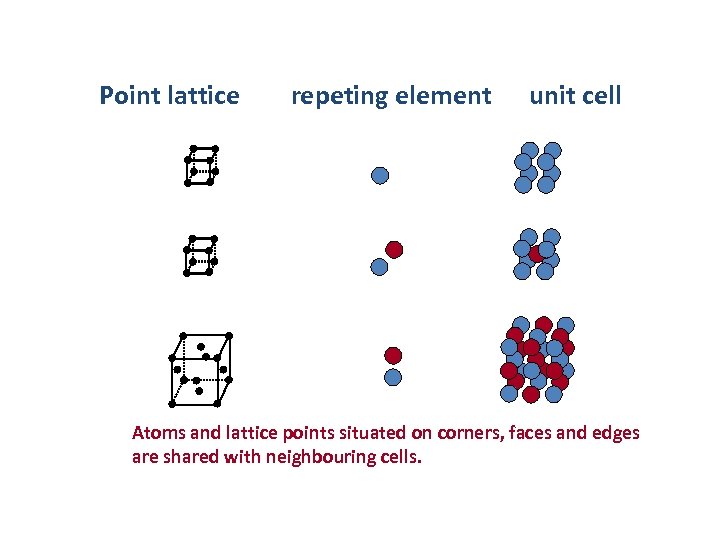
Point lattice repeting element unit cell Atoms and lattice points situated on corners, faces and edges are shared with neighbouring cells.

Unit cell Elementary unit of volume! - Defined by three non planar lattice vectors: a, b and c c α β γ a b -or by the length of the vectors a, b and c and the angles between them (alpha, beta, gamma). The origin of the unit cells can be described by a translation vector t: t=ua + vb + wc The atom position within the unit cell can be described by the vector r: r = xa + yb + zc

Axial systems The point lattices can be described by 7 axial systems (coordinate systems) z Axial system a x γ b y a≠b≠c α≠β≠γ≠ 90 o Monoclinic a≠b≠c α=γ=90 o ≠ β Orthorombic a≠b≠c α= β=γ=90 o Tetragonal a=b≠c α= β=γ=90 o Cubic β α Angles Triclinic c Axes a=b=c α= β=γ=90 o Hexagonal a 1=a 2=a 3≠c α= β=90 o γ=120 o Rhombohedral a=b=c α= β=γ ≠ 90 o

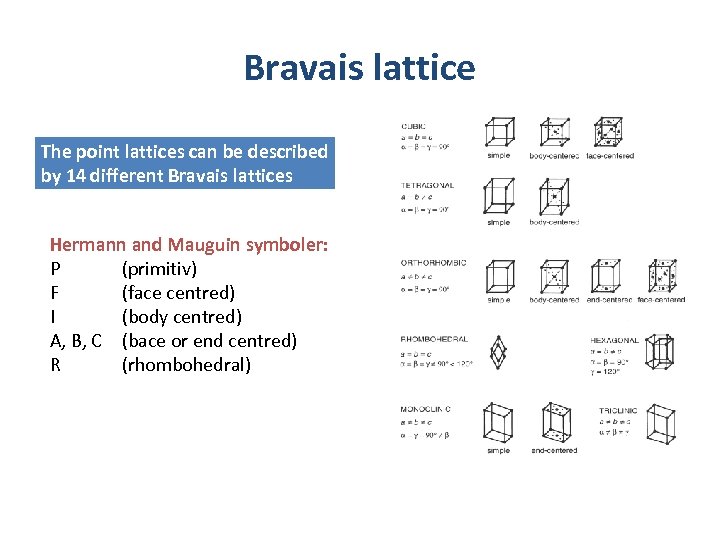
Bravais lattice The point lattices can be described by 14 different Bravais lattices Hermann and Mauguin symboler: P (primitiv) F (face centred) I (body centred) A, B, C (bace or end centred) R (rhombohedral)

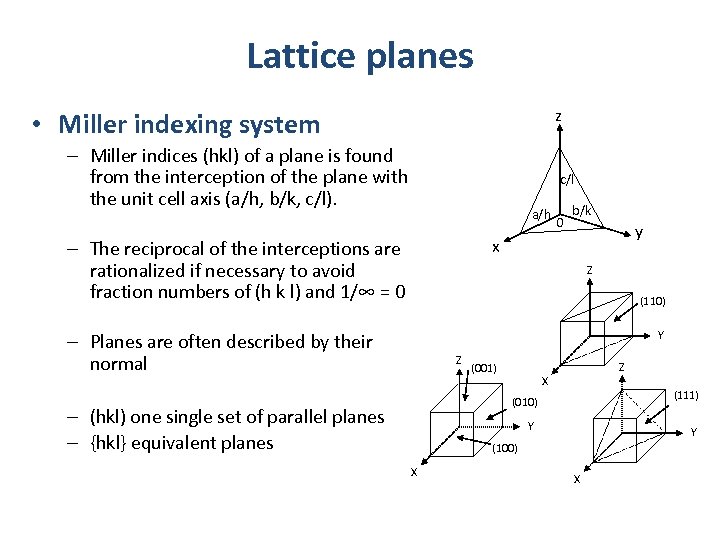
Lattice planes z • Miller indexing system – Miller indices (hkl) of a plane is found from the interception of the plane with the unit cell axis (a/h, b/k, c/l). c/l a/h 0 b/k y x – The reciprocal of the interceptions are rationalized if necessary to avoid fraction numbers of (h k l) and 1/∞ = 0 Z (110) Y – Planes are often described by their normal Z Z (001) X (111) (010) – (hkl) one single set of parallel planes – {hkl} equivalent planes Y Y (100) X X

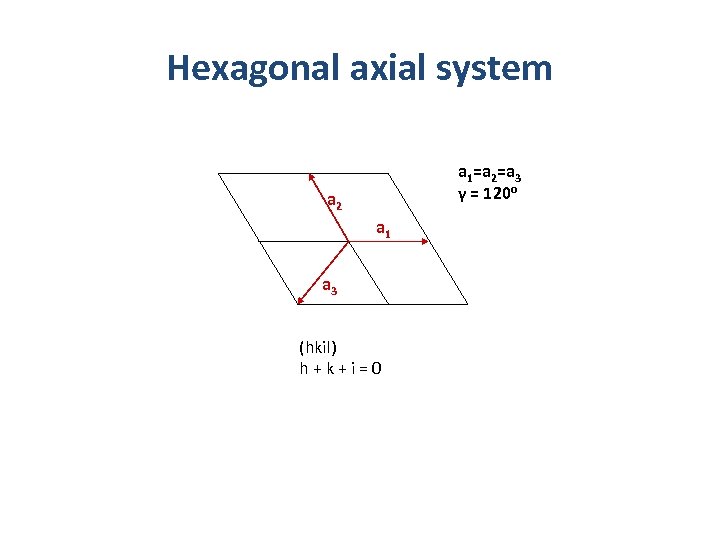
Hexagonal axial system a 1=a 2=a 3 γ = 120 o a 2 a 1 a 3 (hkil) h+k+i=0

Directions • The indices of directions (u, v and w) can be found from the components of the vector in the axial system a, b, c. wc [uvw] c • The indices are scaled so that all are integers and as small as possible • Notation – [uvw] one single direction or zone axis – <uvw> geometrical equivalent directions • [hkl] is normal to the (hkl) plane in cubic axial systems z ua a b vb y x

Determination of the Bravais-lattice of an unknown crystalline phase Tilting series around common axis 27 o 50 nm 15 o 10 o 0 o

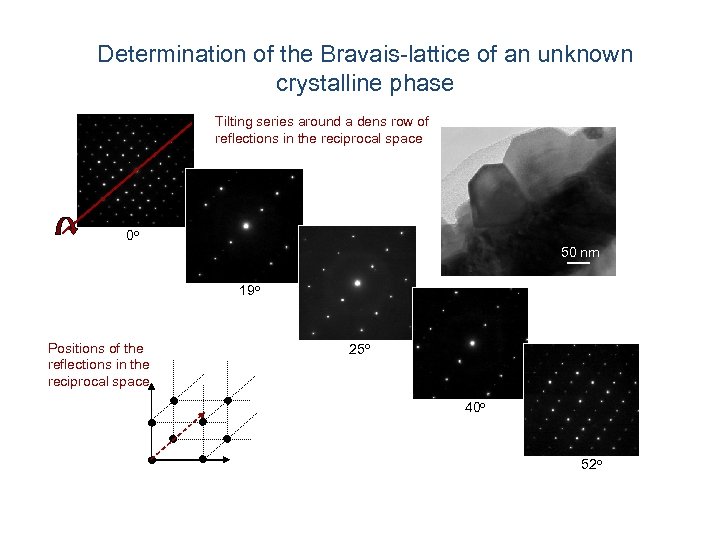
Determination of the Bravais-lattice of an unknown crystalline phase Tilting series around a dens row of reflections in the reciprocal space 0 o 50 nm 19 o Positions of the reflections in the reciprocal space 25 o 40 o 52 o

Bravais-lattice and cell parameters 011 111 001 c 101 b 010 a 110 [100] [011] [101] d=Lλ/R 100 6. 04 Å From the tilt series we find that the unknown phase has a primitive orthorhombic Bravias-lattice with cell parameters: a= 6, 04 Å, b= 7. 94 Å og c=8. 66 Å 7. 94 Å 6 8. 6 Å α= β= γ= 90 o

Resiprocal lattice Important for interpretation of ED patterns Defined by the vectors a*, b* and c* which satisfy the relations: a*. a=b*. b=c*. c=1 and a*. b=b*. c=c*. a=a*. c=……. . =0 Solution: a* is normal to the plane containing b and c etc. Unless a is normal to b and c, a* is not parallel to a. V: Volume of the unit cell V=a. (bxc)=b. (cxa)=c. (axb) Orthogonal axes: a* = 1/Ia. I, b*=1/Ib. I, c*=1/Ic. I

Reciprocal vectors, planar distances –The resiprocal vector is normal to the plane (hkl). and the spacing between the (hkl) planes is given by Unit normal vector: n= ghkl/Ighkl. I Convince your self ! What is the dot product beteen the normal to a (hkl) plane with a vector In the (hkl) plane? • Planar distance (d-value) between planes {hkl} in a cubic crystal with lattice parameter a: