5c6869b0a774c617a9127e10844d191b.ppt
- Количество слайдов: 70

SAT Problem Definition KR with SAT Tractable Subclasses DPLL Search Algorithm Slides by: Florent Madelaine Roberto Sebastiani Edmund Clarke Sharad Malik Toby Walsh Thomas Stützle Kostas Stergiou KNOWLEDGE REPRESENTATION & REASONING - SAT 1

Material of lectures on SAT definitions n Tractable subclasses n n Algorithms for SAT g · Basic chronological backtracking algorithm · Branching heuristics · Look-ahead (propagation) · Backjumping and learning Horn-SAT g 2 -SAT g n CNF DPLL-based g Local Search · GSAT · Walk. SAT · Other enhancements n Application of SAT g g Planning as satisfiability Hardware verification KNOWLEDGE REPRESENTATION & REASONING - SAT 2

Local Search for SAT n Despite the success of modern DPLL-based solvers on real problems there are still very large (and hard) instances that are out of their reach Some random SAT problems really are hard! g Chaff’s and the other complete solvers’ tricks don’t work so well here g · Especially conflict-directed backjumping and learning n Local search methods are very successful on a number of such instances they can quickly find models, if models exist g …but cannot prove insolubility if no models exists g KNOWLEDGE REPRESENTATION & REASONING - SAT 3

k-SAT n Subclass of the SAT problem g n 3 -SAT is NP-complete g n Exactly k variables in each clause (P Q) (Q R) ( R P) is in 2 -SAT can be reduced to 3 -SAT 2 -SAT is in P g Exists linear time algorithm KNOWLEDGE REPRESENTATION & REASONING - SAT 4

Experiments with 3 -SAT n Where are the hard 3 -SAT problems? n Sample randomly generated 3 -SAT · · Fix number of clauses, l Number of variables, n By definition, each clause has 3 variables Generate all possible clauses with uniform probability KNOWLEDGE REPRESENTATION & REASONING - SAT 5
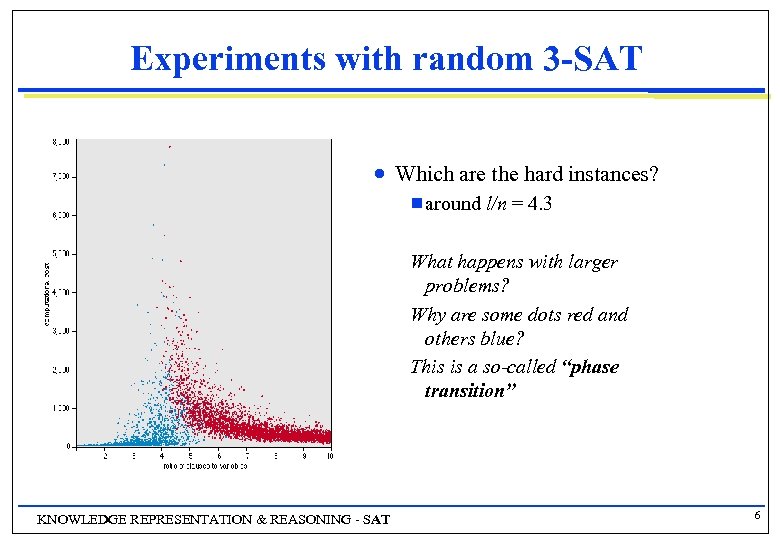
Experiments with random 3 -SAT n Which are the hard instances? g around l/n = 4. 3 What happens with larger problems? Why are some dots red and others blue? This is a so-called “phase transition” KNOWLEDGE REPRESENTATION & REASONING - SAT 6
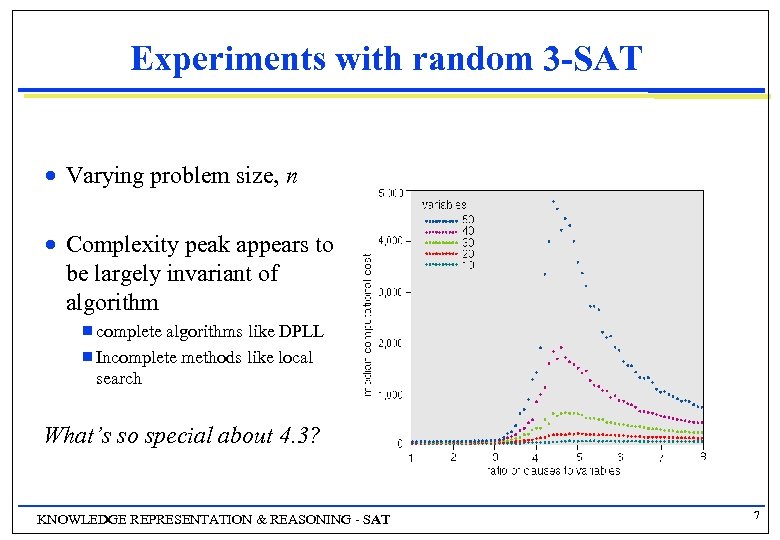
Experiments with random 3 -SAT n Varying problem size, n n Complexity peak appears to be largely invariant of algorithm g complete algorithms like DPLL g Incomplete methods like local search What’s so special about 4. 3? KNOWLEDGE REPRESENTATION & REASONING - SAT 7
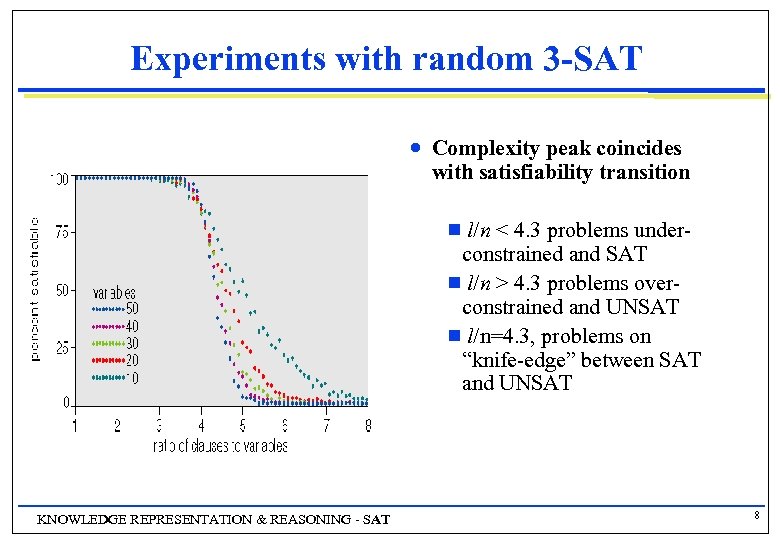
Experiments with random 3 -SAT n Complexity peak coincides with satisfiability transition l/n < 4. 3 problems underconstrained and SAT g l/n > 4. 3 problems overconstrained and UNSAT g l/n=4. 3, problems on “knife-edge” between SAT and UNSAT g KNOWLEDGE REPRESENTATION & REASONING - SAT 8

Phase Transitions n Similar “phase transitions” for other NP-hard problems q q n job shop scheduling traveling salesperson exam timetabling constraint satisfaction problems Was a “hot research topic” until recently: q q predict hardness of a given instance & use hardness to control search strategy but real problems with structure are much different than random ones… KNOWLEDGE REPRESENTATION & REASONING - SAT 9

Local Search Methods n Can handle “big” random SAT problems g g n Also handle big structured SAT problems g n Can go up about 10 x bigger than systematic solvers! Rather smaller than structured problems (espec. if ratio 4. 26) But lose here to best systematic solvers Try hard to find a good solution g Very useful for approximating MAX-SAT · g g the optimization version of SAT Not intended to find all solutions Not intended to show that there are no solutions (UNSAT) KNOWLEDGE REPRESENTATION & REASONING - SAT 10
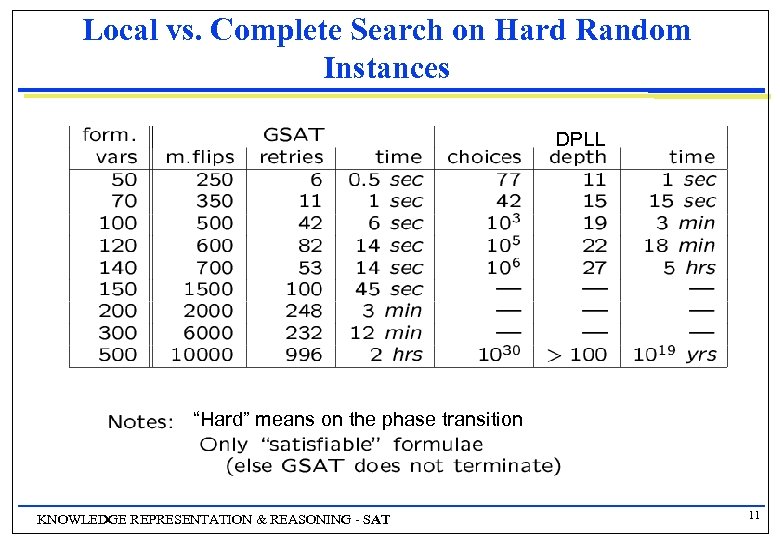
Local vs. Complete Search on Hard Random Instances DPLL “Hard” means on the phase transition KNOWLEDGE REPRESENTATION & REASONING - SAT 11

Problem Formulation for Complete Search INPUT: some initial state and a set of goal states n BASIC ACTIONS: explore a successor of a visited state. n PATH COSTS: sum of the step costs n SOLUTION: a path from the initial state to one of the goal states through the state space. n OPTIMAL SOLUTION: a solution of lowest cost n QUESTION: Find a (optimal) solution. n KNOWLEDGE REPRESENTATION & REASONING - SAT 12

Problem Formulation for Local Search INPUT: some initial state n BASIC ACTIONS: move from the current state to a successor state. n EVALUATION FUNCTION: gives the score of a state n SOLUTION: state with the highest score. n KNOWLEDGE REPRESENTATION & REASONING - SAT 13

Local Search Techniques n n Typically ignore large portions of the search space and are based on complete initial formulation of the problem deterministic: (steepest) Hill Climbing (greedy local search) g Local beam search g Tabu search g n stochastic: Stochastic Hill Climbing g Simulated annealing g Genetic algorithms g Ant colony optimisation g q They have one important advantage: they work on large instances because they only keep track of few states. KNOWLEDGE REPRESENTATION & REASONING - SAT 14

Steepest Hill Climbing starts from initial state while there is a better successor do move to the best successor end while n This method has one important drawback: it may return a bad solution because it can get stuck on a local optimum and is very dependent of the initial state g a local optimum is a state where there is no successor better than the current state, but there are other states that are better KNOWLEDGE REPRESENTATION & REASONING - SAT 15

Problems with Hill Climbing n Foothills / Local Optimal: No neighbor is better, but not at global optimum. g n Plateaus: All neighbors look the same. g n (8 -puzzle: perhaps no action will change # of tiles out of place) Ridge: going up only in a narrow direction. g n (Maze: may have to move AWAY from goal to find (best) solution) Suppose no change going South, or going East, but big win going SE Ignorance of the peak: Am I done? KNOWLEDGE REPRESENTATION & REASONING - SAT 16

Improving the Hill Climbing Procedure n Using random restarts q n By allowing sideways move q n avoid states that will get you stuck (tabu search) By enlarging the size of the neighbourhood q n when stuck move to successor states worth the same as the current one By allowing some limited memory q n when stuck start again from another initial state change successor function to generate more states By allowing transition to worse states q when stuck allow moves to successor states worse than the current one KNOWLEDGE REPRESENTATION & REASONING - SAT 17

Local Search for SAT n Choose a random initial state I g n i. e. a random assignment of 0 or 1 to all variables If I is not a model, repeatedly choose a variable p and change its value in I (flip the variable) g flip(I, p) determines the successor state The flipped variables are chosen using heuristics or randomly, or both g n q the evaluation function is usually the number of satisfied clauses in a state most algorithms use random restart if no solution has been found after a fixed number of search steps Several instantiations of this general framework have been proposed KNOWLEDGE REPRESENTATION & REASONING - SAT 18

Definitions n Positive/Negative/Net Gain g g n Given candidate variable assignment T for CNF formula F, let B 0 be the total # of clauses that are currently unsatisfied in F. Let T’ be the state of F if variable V is flipped. Let B 1 be the total # of clauses which would be unsatisfied in T’. The net gain of V is B 0 -B 1. The negative gain of V is the # of clauses which are satisfied in T but unsatisfied in T’. The positive gain of V is the # of clauses which are unsatisfied in T but satisfied in T’. Variable Age g The age of a variable is the # of flips since it was last flipped. KNOWLEDGE REPRESENTATION & REASONING - SAT 19

GSAT & GWSAT n The GSAT Algorithm (Selman, Mitchell, Levesque, 1992) search initialisation: randomly chosen assignment q in each search step, flip the variable which gives the maximal increase in the number of satisfied claused (maximum net gain) q Ø q n n ties are broken randomly if no model found after max. Steps steps, restart from another randomly chosen assignment HSAT (Gent and Walsh, 1993) – Same as GSAT, but break ties in favor of maximum age variable. The GWSAT Algorithm (Selman, Kautz, Cohen, 1994) search initialisation: randomly chosen assignment q Random Walk step: randomly choose a currently unsatisfied clause and a literal in that clause, flip the corresponding variable to satisfy this clause q GWSAT steps: choose probabilistically between a GSAT step and a Random Walk step with ‘walk probability’ (noise) π q KNOWLEDGE REPRESENTATION & REASONING - SAT 20

Walk. SAT n The. Walk. SAT algorithm family g g search initialisation: randomly chosen assignment search step 1) randomly select a currently unsatisfied clause 2) select a literal from this clause according to a heuristic h g n if no model found after max. Steps steps, restart from randomly chosen assignment Original Walksat (Selman, Kautz, Cohen 1994) g g g Pick random unsatisfied clause BC. If any variable in BC has negative gain of 0, randomly select one. Otherwise, with probability p, select random variable from BC to flip, and with probability (1 -p), select variable in BC with minimal negative gain (break ties randomly). KNOWLEDGE REPRESENTATION & REASONING - SAT 21

Walk. SAT Beating a correct, optimized implementation of Walksat is difficult. n Many variants of “walksat” appear in literature n Many of them are incorrect interpretations/ implementations of [Selman, Kautz, Cohen] Walksat. g Most of them perform significantly worse. g None of them performs better. g Positive gain: #clauses that were unsatisfied and now become satisfied n Negative gain: #clauses that were satisfied and now become unsatisfied n KNOWLEDGE REPRESENTATION & REASONING - SAT 22

Variations of Walk. SAT n n n SKC: Select variable such that minimal number of currently satisfied clauses become unsatisfied by flipping; if ‘zero-damage’ possible, always go for it; otherwise, with probability wp variable is randomly selected. Tabu: Select variable that maximises increase in total number of satisfied clauses when flipped; use constant length tabu-list for flipped variables and random tiebreaking. Tabu search prevents returning quickly to same state. g To implement: Keep fixed length queue (tabu list). g Add most recent step to queue; drop oldest step. g Never make step that's on current tabu list. n Example: g without tabu: · flip v 1, v 2, v 4, v 2, v 10, v 11, v 10, v 3, . . . g with tabu (length 4)—possible sequence: · flip v 1, v 2, v 4, v 10, v 11, v 3, . . . KNOWLEDGE REPRESENTATION & REASONING - SAT 23
![SAT Local Search: Novelty Family n Novelty [Mc. Allester, Selman, Kautz 1997] g g SAT Local Search: Novelty Family n Novelty [Mc. Allester, Selman, Kautz 1997] g g](https://present5.com/presentation/5c6869b0a774c617a9127e10844d191b/image-24.jpg)
SAT Local Search: Novelty Family n Novelty [Mc. Allester, Selman, Kautz 1997] g g g n n Pick random unsatisfied clause BC. Select variable v in BC with maximal net gain, unless v has the minimal age in BC. In the latter case, select v with probability (1 -p); otherwise, flip v 2 with 2 nd highest net gain. Novelty+ [Hoos and Stutzle 2000] – Same as Novelty, but after BC is selected, with probability pw, select random variable in BC; otherwise continue with Novelty R-Novelty [Mc. Allester, Selman, Kautz 1997] and R-Novelty+ [Hoos and Stutzle 2000]– similar to Novelty/Novelty+, but more complex. KNOWLEDGE REPRESENTATION & REASONING - SAT 24

Adaptive Novelty+ (current winner) n with probability 1% (the “+” part) g n else be greedier (other 99%) g g g n Choose randomly among all variables that appear in at least one unsatisfied clause Randomly choose an unsatisfied clause C (the “novelty” part) · Flipping any variable in C will at least fix C Choose the most-improving variable in C … except … with probability p, ignore most recently flipped variable in C The “adaptive” part: g g g If we improved # of satisfied clauses, decrease p slightly If we haven’t got an improvement for a while, increase p If we’ve been searching too long, restart the whole algorithm KNOWLEDGE REPRESENTATION & REASONING - SAT 25

Structure of the standard SAT locals search variable selection heuristics n Score variables with respect to gain metric Walksat uses negative gain, g GSAT and Novelty use net gain. g n Restricted set of candidate variables GSAT – any var in formula; g Walksat/Novelty – pick variable from a single random unsatisfied clause g n Ranking of variables with respect to scoring metric g n Greedy choices considered by all heuristics. Novelty variants also consider 2 nd best variable. Variable Age – prevent cycles and force exploration g Novelty variants, HSAT, Walksat+tabu KNOWLEDGE REPRESENTATION & REASONING - SAT 26

Some observations on the variable selection heuristics n n Difficult to determine a priori how effective any given heuristic is. Many heuristics look similar to Walksat, but performance varies significantly (c. f. [Mc. Allester, Selman, Kautz 1997] Empirical evaluation necessary to evaluate complex heuristics. Previous efforts to discover new heuristics involved significant experimentation. Humans are skilled at identifying primitives, but find it difficult/time-consuming to combine the primitives into effective composite heuristics. KNOWLEDGE REPRESENTATION & REASONING - SAT 27

Simulated Annealing (popular general local search technique – often very effective, rather slow) n Simulated Annealing is an SLS method that tries to avoid local optima by accepting probabilistically moves to worse solutions. Simulated Annealing was one of the first SLS methods g now a "mature" SLS method g many applications available (ca. 1, 000 papers) g (strong) convergence results g simple to implement g inspired by an analogy to physical annealing g KNOWLEDGE REPRESENTATION & REASONING - SAT 28

Simulated Annealing description n Given a solution s generate some neighboring solution s’ N(s) g by picking a variable at random and flipping it if f(s’) f(s) then accept s’ n if f(s’) > f(s) then a probabilistic yes/no decision is made n if outcome is yes, then s’ replaces s g if outcome is no, then s is kept g n probabilisitic decision depends on the difference f(s’) - f(s) g a control parameter T, called temperature g KNOWLEDGE REPRESENTATION & REASONING - SAT 29

Simulated Annealing description n Pick a variable at random If flipping it improves assignment: do it. Else flip anyway with probability p = e- /T where g = f(s’) - f(s) (i. e. damage to score) · What is p for =0? For large ? g T = “temperature” · What is p as T tends to infinity? · · Higher T = more random, non-greedy exploration As we run, decrease T from high temperature to near 0. KNOWLEDGE REPRESENTATION & REASONING - SAT 30

Simulated Annealing Algorithm KNOWLEDGE REPRESENTATION & REASONING - SAT 31

Simulated Annealing general issues n generation of neighboring solutions often: generate a random neighboring solution s’ N(s) g possibly better: systematically generate neighboring solutions => at least we are sure to sample the whole neighbourhood if no move is accepted g n acceptance criterion g often used: Metropolis acceptance criterion · If f(s’) f(s) then accept s’ · if f(s’) > f(s) then accept it with a probability of e- /T , where = f(s’) - f(s) KNOWLEDGE REPRESENTATION & REASONING - SAT 32

Simulated Annealing cooling schedule n open questions how to define the control parameter? g how to define the (inner and outer) loop criteria? g n cooling schedule g initial temperature T 0 (Example: base it on some statistics about cost values, acceptance ratios etc. ) g temperature function — how to change the temperature (Example: geometric cooling, Tn+1 = a. Tn, n=0, 1, … 0<a<1) g number of steps at each temperature (inner loop criterion) (Example: multiple of the neighbourhood size) g termination criterion (outer loop criterion) (Example: no improvement of sbest for a number of temperature values and acceptance rate below some critical value) KNOWLEDGE REPRESENTATION & REASONING - SAT 33

Simulated Annealing theoretical results n if SA can be run long enough with an infinite number of temperature values g and for each temperature value with an infinite number of steps g one can be sure to be at an optimal solution at the end n however, it is not clear what end means n in addition, when run at a single temperature level long enough we can be sure to find the optimum solution g hence, an optimal solution can be found without annealing g one only needs to store the best solution found and return it at the end g n BUT: we need n -> to guarantee optimality KNOWLEDGE REPRESENTATION & REASONING - SAT 34

Simulated Annealing theoretical results n From theoretical proofs we can also conclude that g n better solutions are becoming more likely this gives evidence that after a sufficient number of temperature values g a sufficient number of steps at each temperature g chances are high to have seen a good solution n however, it is unclear what sufficient means KNOWLEDGE REPRESENTATION & REASONING - SAT 35

Evolutionary algorithms (another popular general technique) n Many local searches at once g g Consider 20 random initial assignments Each one gets to try flipping 3 different variables (“reproduction with mutation”) Now we have 60 assignments Keep the best 20 (“natural selection”), and continue KNOWLEDGE REPRESENTATION & REASONING - SAT 36
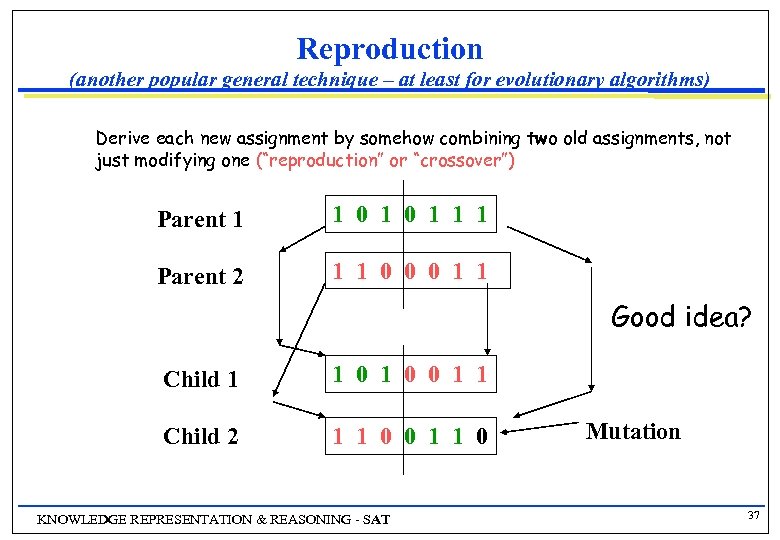
Reproduction (another popular general technique – at least for evolutionary algorithms) Derive each new assignment by somehow combining two old assignments, not just modifying one (“reproduction” or “crossover”) Parent 1 1 0 1 1 1 Parent 2 1 1 0 0 0 1 1 Good idea? Child 1 1 0 0 1 1 Child 2 1 1 0 0 1 1 0 KNOWLEDGE REPRESENTATION & REASONING - SAT Mutation 37

Dynamic Local Search n Dynamic local search is a collective term for a number of approaches that try to escape local optima by iteratively modifying the evaluation function value of solutions. different concept for escaping local optima g several variants available g promising results g KNOWLEDGE REPRESENTATION & REASONING - SAT 38

Dynamic Local Search n n guide the local search by a dynamic evaluation function h(s) composed of g g n n n cost function f(s) penalty function is adapted at computation time to guide the local search penalties are associated to solution features related approaches: g g long term strategies in tabu search noising method usage of time-varying penalty functions for (strongly) constrained problems etc. KNOWLEDGE REPRESENTATION & REASONING - SAT 39

Dynamic Local Search issues n timing of penalty modifications at every local search step g only when trapped in a local optimum g long term strategies for weight decay g n strength of penalty modifications additive vs. multiplicative penalty modifications g amount of penalty modifications g n focus of penalty modifications g choice of solution attributes to be punished KNOWLEDGE REPRESENTATION & REASONING - SAT 40

Example: Guided Local Search (GLS) n guided local search (GLS) modifies penalties when trapped in local optima g variants exist that use occasional penalty decay g uses additive penalty modifications g chooses few among the many solution components for punishment g KNOWLEDGE REPRESENTATION & REASONING - SAT 41

GLS - details KNOWLEDGE REPRESENTATION & REASONING - SAT 42

GLS - details KNOWLEDGE REPRESENTATION & REASONING - SAT 43

GLS for SAT uses the GSAT architecture for local search n uses in addition a special tie-breaking criterion that favors flipping a variable that was flipped the longest time ago n if in x consecutive iterations no improved solution is found, then modify penalties n solution attributes are clauses n when trapped in a local optimum, add penalties to clauses of maximum utility n g which clauses are these? KNOWLEDGE REPRESENTATION & REASONING - SAT 44

GRASP n Greedy Randomized Adaptive Search Procedures (GRASP) is an SLS method that tries to construct a large variety of good initial solutions for a local search algorithm. predecessors: semi-greedy heuristics g tries to combine the advantages of random and greedy solution construction g KNOWLEDGE REPRESENTATION & REASONING - SAT 45

Greedy construction heuristics n Iteratively construct solutions by choosing at each construction step one solution component g solution components are rated according to a greedy function g the best ranked solutions component is added to the current partial solution examples: Kruskal’s algorithms for minimum spanning trees, greedy heuristic for the TSP, n advantage: generate good quality solutions; local search runs fast and finds typically better solutions than from random initial solutions n disadvantage: do not generate many different solutions; difficulty of iterating n KNOWLEDGE REPRESENTATION & REASONING - SAT 46

Random vs. greedy construction n random construction high solution quality variance g low solution quality g n greedy construction good quality g low (no) variance g n goal: exploit advantages of both KNOWLEDGE REPRESENTATION & REASONING - SAT 47

Semi-greedy heuristics add at each step not necessarily the highest rated solution component n repeat until a full solution is constructed: n rate solution components according to a greedy function g put high rated solution components into a restricted candidate list (RCL) g choose one element of the RCL randomly and add it to the partial solution g adaptive element: greedy function depends on the partial solution constructed so far g KNOWLEDGE REPRESENTATION & REASONING - SAT 48

Generation of the RCL KNOWLEDGE REPRESENTATION & REASONING - SAT 49

GRASP tries to capture advantages of random and greedy solution construction n iterate through n g randomized solution construction exploiting a greedy probabilistic bias to construct feasible solutions apply local search to improve over the constructed solution n keep track of the best solution found so far and return it at the end n KNOWLEDGE REPRESENTATION & REASONING - SAT 50

GRASP – local search n local search from random solutions high variance g best solution quality often better than greedy (if not too large instances) g average solution quality worse than greedy g local search requires many improvement steps g n local search from greedy solutions average solution quality better than random g local search typically requires only a few improvement steps g low (no) variance g KNOWLEDGE REPRESENTATION & REASONING - SAT 51

GRASP for SAT KNOWLEDGE REPRESENTATION & REASONING - SAT 52

GRASP for SAT KNOWLEDGE REPRESENTATION & REASONING - SAT 53

Local Search Summary n Surprisingly efficient search technique g n Wide range of applications g n Especially for randomized local search Intuitive explanation: g n Not only SAT Formal properties elusive g n Many variants proposed Search spaces are too large for systematic search anyway. . . Area will most likely continue to thrive KNOWLEDGE REPRESENTATION & REASONING - SAT 54

Dynamic SAT n The SAT framework is successful in modeling and solving numerous practical problems AI (scheduling and planning, resource allocation, timetabling, temporal reasoning, etc. ) g Hardware and software verification, model checking g n Some assumptions are made: g All components of the problem to solve (variables, clauses) are completely known before modeling and solving g and do not change during or after this process g that is, the problems are static KNOWLEDGE REPRESENTATION & REASONING - SAT 55
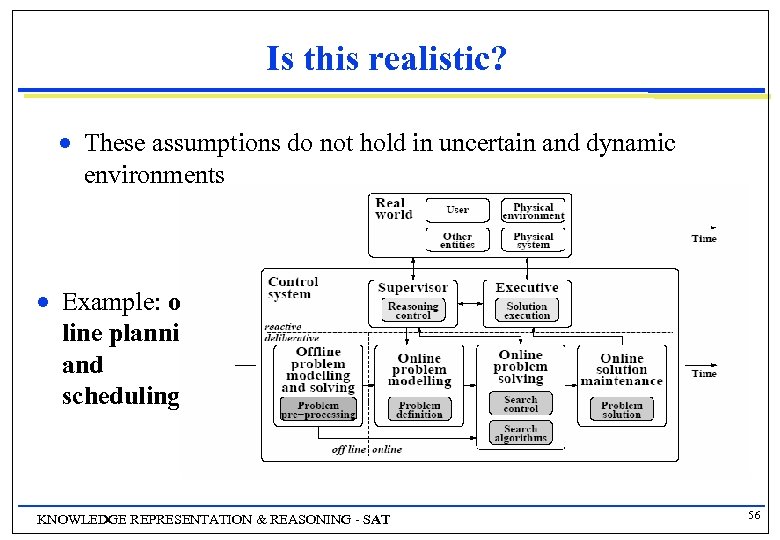
Is this realistic? n n These assumptions do not hold in uncertain and dynamic environments Example: online planning and scheduling KNOWLEDGE REPRESENTATION & REASONING - SAT 56

Difficulties with on-line solving n Difficulties in modeling and solving in such environments are due to two facts: g g n Knowledge about the real world is often incomplete, imprecise, and uncertain The real world and the knowledge about is may change during or after modeling and solving These difficulties make the use of the standard SAT framework infeasible KNOWLEDGE REPRESENTATION & REASONING - SAT 57

Travel Management System n A TMS is embedded in a car and manages all features of long travel g g g n Uncertainty may come from g n Route, stops, rendezvous, refueling, maintenance physical system -> car user -> car driver physical environment -> road, traffic, weather, etc. other entities -> hotels, people, garages, other TMSs car, environment, and other entities Changes may occur at any time from g driver, car, environment, and other entities KNOWLEDGE REPRESENTATION & REASONING - SAT 58

Uncertainty and Change n Present not only in planning and scheduling g Online computer vision, failure diagnosis, and situation tracking Computer-aided system design and configuration Interactive or distributed problem solving · Uncertainties about the decisions of the users or the other entities (agents) g Financial portfolio management · Uncertainties about the prices of stocks g Etc. KNOWLEDGE REPRESENTATION & REASONING - SAT 59

Requirements in uncertain and dynamic situations n Limit as much as possible the need for repeated solving g n time consuming and disturbing for the user (as new solutions keep arriving) Limit as much as possible the changes in the produced solutions g g when the current one is no longer valid important changes are undesirable · imagine completely changing the route because it has started to rain KNOWLEDGE REPRESENTATION & REASONING - SAT 60

Requirements in uncertain and dynamic situations n Limit as much as possible the computing time and resources g Often the utility of the solution decreases with the time of its delivery · Telling the driver to exit the highway after the exit was passed is useless n Keep producing consistent and (if possible) optimal solutions g Hard constraints cannot be violated and optimality is always desirable · but it may conflict with the previous requirement… KNOWLEDGE REPRESENTATION & REASONING - SAT 61

Dynamic SAT (DSAT) n n A DSAT is a sequence of SAT problems each resulting from the previous one through changes in its definition These changes may affect any SAT component g g g Addition or removal of variables Addition or removal of clauses Changes in existing clauses · addition or removal of literals n How can we solve such problems efficiently: g Best answer: Local Search! KNOWLEDGE REPRESENTATION & REASONING - SAT 62

DSAT Assignment n In this assignment you will implement and experimentally evaluate local search algorithms for DSAT The experimental evaluation will be carried out on randomly generated k-SAT problems g you will also run a complete solver on the generated instances g dynamic changes will be implemented through the sequential addition of clauses g n You will work in teams of 3 all 3 members of a team will be individually examined during the presentation of your work g the presentation will be sometime in January/February (tbc later) g there will a “progress so far” discussion on December 8/9 g KNOWLEDGE REPRESENTATION & REASONING - SAT 63

DSAT Assignment n The assignment consists of the following steps: 1. Build a generator for random k-SAT instances (k 3) g g g This part of the assignment is common to both teams. You must use the same generator so that the algorithms can be fairly compared The generator will take as input 3 parameters: <k, n, l, m>, where n is the number of variables, l the number of clauses contained in the initial problem, and m is the number of clauses dynamically added at each step g m can be a percentage Each clause will be “filled” with k variables chosen uniformly at random. After a variable is chosen it will be negated with probability 0. 5. g You must make sure that no variable appears in a clause more than once (in any polarity) g You must make sure that no clause appears more than once in the set of l clauses g you don’t need to check for subsumption between the generated clauses KNOWLEDGE REPRESENTATION & REASONING - SAT 64

DSAT Assignment n The assignment consists of the following steps: 2. Once a problem is generated you will have to check if it is satisfiable. This can be by running a complete solver (minisat, tinisat, zchaff, …) g if it is not satisfiable then you throw it away and create a new one g NOTE: by setting the parameters n and l properly you can ensure that almost all generated instances are satisfiable g g g Experimentation needed to find the proper values of the parameters ATTENTION: we don’t want very easy problems! But they don’t have to be extremely hard If the problem is satisfiable you need to identify and store the first solution found g You may need to make minimal changes in the solver’s code if the solver does not return the solution by default KNOWLEDGE REPRESENTATION & REASONING - SAT 65

DSAT Assignment n The assignment consists of the following steps: 3. Once a satisfiable problem has been generated and a solution has been found, you can dynamically alter it by adding m clauses at random g g One option you can use to create many instances starting from the same initial problem, is to repeat the above process many times g In this way you will get many DSAT instances that are all derived from the same basic problem by adding m clauses in one step Another option is to continue adding m clauses for some fixed number of x steps. g In this way you will get a sequence 1, 2, …, x of DSAT instances where instance i is derived from instance i-1 by adding m clauses The whole process can be repeated many times (i. e. for many initial SAT randomly created SAT problems). NOTE: If you use the same random seed then the problems created will be the same g you should store the seeds used so that the two teams can compare their algorithms on the same instances KNOWLEDGE REPRESENTATION & REASONING - SAT 66

DSAT Assignment n The assignment consists of the following steps: 4. each time a DSAT instance is created, run a local search algorithm using the previously found solution as starting point g g The algorithm runs until a new solution is found or a termination condition becomes true (i. e. it reaches the step limit) g When it terminates you should store the last assignment found whether it is a solution or not! NOTE: If you are using the first option for DSAT generation the previous problem will always be the initial one and therefore you will have a solution for that problem g But if you are using the second option the local search algorithm may not have found a solution for the previous instance in the sequence. In this case what is the initial assignment used by the local search algorithm? g HINT: you can start from the assignment reached by the previous run ignoring the fact that it was not an actual solution KNOWLEDGE REPRESENTATION & REASONING - SAT 67

DSAT Assignment n Which local search algorithms will you implement? g Each team will implement one “simple” and one “complex” local search method · · · n “simple” methods are WSAT and its variants (Novelty, etc. ) “complex” methods are dynamic local search (GLS) and GRASP Simulated Annealing and Genetic Algorithms are not considered. Why? How will you measure the performance of the algorithms? You need to report how many instances are solved, and for each instance that is not solved, the number of conflicting clauses (this is 0 for a solved instance) 2. For each instance (solved or not) you need to report the distance of the assignment returned from the initial solution 1. g g n distance is measured as the number of different variable assignments in the case of a sequence of DSATs, the average distance between consecutive problems What about the various parameters of the algorithms? g You need to read the corresponding papers carefully to find the proposed values of the parameters. · However, tuning a local search method is largely an experimental process. You will find the “optimal” settings through experiments. KNOWLEDGE REPRESENTATION & REASONING - SAT 68

DSAT Assignment n As important issue in DSAT is finding solutions “close” to the previous ones g n Question: How will deal with this? g n Local search algorithms for SAT are not concerned with this and thus ignore it will you have to modify the evaluation function in some way? Answer: You don’t have to deal with it! g It is a research problem that has not been addressed yet g If one of you chooses to do his Master’s thesis on SAT then this is an interesting problem to tackle On December 8/9 I expect to hear the two teams’ proposals on how to implement the chosen local search methods KNOWLEDGE REPRESENTATION & REASONING - SAT 69

Conclusions n SAT is a very useful problem class q Theoretical importance · prototypical NP-complete problem · NP-completeness is usually proved by reduction to SAT q Practical value · can be used to represent and reason with knowledge in many domains q Efficient Algorithms · complete DPLL-based solvers and incomplete local search procedures have been very successful in solving large hard real problems KNOWLEDGE REPRESENTATION & REASONING - SAT 70
5c6869b0a774c617a9127e10844d191b.ppt