Величины.pptx
- Количество слайдов: 17

Санкт-Петербургское государственное бюджетное профессиональное образовательное учреждение «Педагогический колледж № 8» Маркина О. А. Величина и её измерение

Величины — это особые свойства реальных объектов или явлений. Например, свойство предметов иметь протяженность называется длиной. Это же слово мы употребляем, когда говорим о протяженности конкретных объектов. Однородные величины выражают одно и то же свойство объектов некоторого множества. Разнородные величины выражают различные свойства объектов. Длина и площадь — это разнородные величины. Величины — длина, площадь, масса и другие обладают рядом свойств: 1. Любые две величины одного рода сравнимы: они либо равны, либо одна меньше другой. Для величин одного рода имеют место отношения «равно» , «меньше» и «больше» и для любых величин a и b справедливо одно и только одно из отношений: а<b, а = b, а>b.

2. Величины одного рода можно складывать, в результате сложения получится величина того же рода. Для любых двух величин а и b однозначно определяется величина а + b, её называют суммой величин а и b. Например, если а — длина отрезка АВ, b — длина отрезка ВС , то длина отрезка АС есть сумма длин отрезков АВ и ВС. 3. Величину умножают на действительное число, получая в результате величину того же рода. Для любой величины а и любого неотрицательного действительного числа х существует единственная величина b = x ·a; величину b называют произведением величины а на число х. Например, если длину а отрезка АВ умножить на x = 2, то получим длину 2 а нового отрезка АС.

4. Величины одного рода вычитают, определяя разность величин через сумму: разностью величин а и b называется такая величина с, что а = b+с. Например, если а — длина отрезка АС, b—длина отрезка АВ, то длина отрезка ВС есть разность длин отрезков АС и АВ. 5. Величины одного рода делят, определяя частное через произведение величины на число: частным величин а и b называется такое неотрицательное действительное число х, что а = x·b. Чаще это число х называют отношением величин а и b и записывают в таком виде: Например, отношение длины отрезка АС к длине отрезка АВ равно 2.

Упражнения. 1. Имеются два куска проволоки. Каким образом можно сравнить их длины, не прибегая к измерению? 2. Имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л воды? 3. Как с помощью двух бидонов емкостью 17 литров и 5 литров отлить из молочной цистерны 13 литров молока? 4. Как можно сравнить массы двух предметов, не определяя массу каждого из них? 5. На рисунке изображены два прямоугольника, имеющие площади а и b. Постройте прямоугольник, площадь которого равна: 1). a+b; 2) 5 а; 3) ; 4) b-а a b

Понятие измерения величины Измерение заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей — другой, для масс — третий и т. д. Но каким бы ни был этот процесс, в результате измерения величины получается определённое численное значение при выбранной единице. Если дана величина а и выбрана единица величины е, то в результате измерения величины а находят такое действительное число х, что а = х·е. Это число х называют численным значением величины а при единице величины е. Символическая форма: х = mе(а).
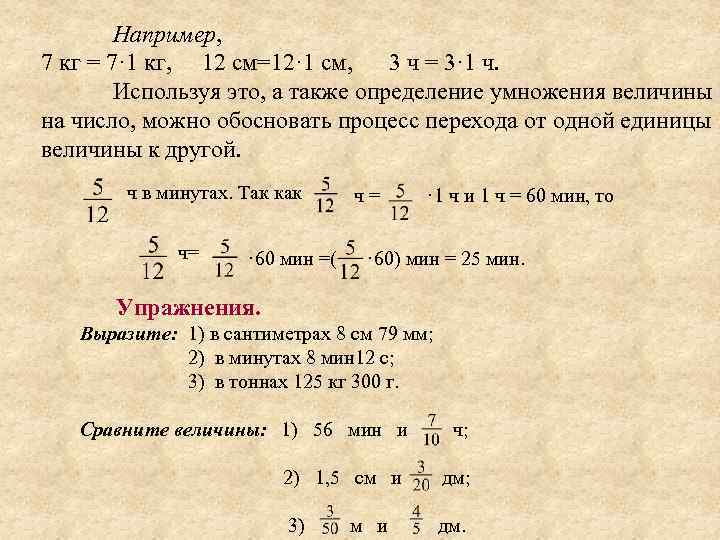
Например, 7 кг = 7· 1 кг, 12 см=12· 1 см, 3 ч = 3· 1 ч. Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой. ч в минутах. Так как ч= · 60 мин =( ч= · 1 ч и 1 ч = 60 мин, то · 60) мин = 25 мин. Упражнения. Выразите: 1) в сантиметрах 8 см 79 мм; 2) в минутах 8 мин 12 с; 3) в тоннах 125 кг 300 г. Сравните величины: 1) 56 мин и ч; 2) 1, 5 см и дм; 3) дм. м и

Величины, которые вполне определяются одним численным значением, называются скалярными величинами. Например, длина, площадь, объем, масса. Кроме скалярных величин, в математике рассматривают ещё векторные величины. Для определения векторной величины необходимо указать не только её численное значение, но и направление. Например, векторными величинами являются сила, ускорение, напряженность электрического поля и. др. Измерение величин позволяет свести сравнение их к сравнению чисел, операции над величинами к соответствующим операциям над числами. 1. Если величины а и b измерены при помощи единицы величины е, то отношения между величинами а и в будут такими же, как и отношения между их численными значениями, и наоборот: Например, если массы двух тел таковы, что а = 5 кг, в = 3 кг, то можно утверждать, что масса а больше массы в, поскольку 5>3.

2. Если величины а и b измерены при помощи единицы величины е, то, чтобы найти численное значение суммы а + b, достаточно сложить численные значения величин а и b: а + в= с <=> mе(а + b) = mе(а) + mе (b). Например, если а=15 кг, b=12 кг, то а + b = 15 кг +12 кг = (15+12) кг = 27 кг. 3. Если величины а и b таковы, что b = х·а, где х — положительное действительное число, и величина а измерена при помощи единицы величины е, то, чтобы найти численное значение величины b при единице е, достаточно число х умножить на число mе (а): b = ха <=> mе (b) = х • mе (а). Например, если масса b в 3 раза больше массы а, т. е. b = 3 а, и а = 2 кг, то b = 3 а = 3·(2 кг) = (3· 2) кг=6 кг. Примеры. 1. Существуют ли три точки А, В, С такие, что: а) АС=12 см, АВ=8 см, ВС=4 см; б) АС=6 см, АВ=12 см, ВС=20 см? 2. Сумма сторон прямоугольника равна 30 см. Чему равны стороны этого прямоугольника, если одна сторона больше смежной стороны в 1, 5 раза? 3. Периметр треугольника 37 см. Одна сторона 12 см, другая сторона составляет 75% длины первой стороны. Чему равна длина третьей стороны?

Упражнения. Решите нижеприведенные задачи и объясните, какие действия над величинами выполнялись в процессе решения: 1) На обработку трёх деталей потратили ч. На первую деталь было израсходовано 0, 25 ч, на вторую Сколько времени пошло на обработку третьей детали? ч. 2) Книга дешевле альбома на 78 к. Сколько стоят два таких альбома, если одна книга стоит 68 к? 3) На нефтебазе было 12680 т бензина. В первый день база отпустила 834 т, во второй — в 2 раза меньше, чем в первый, а в третий — на 229 т больше, чем во второй. Сколько тонн бензина осталось на базе? 4) Из деревянного бруска, имеющего форму прямоугольного параллелепипеда, длина которого 24 см, ширина в 3 раза меньше длины, а высота 11 см, вырезали куб с ребром 6 см. Найдите объём оставшейся части.

Площадь фигуры и её измерение Понятие площади, как и понятие длины, определяется через свойства: Ø Площадь фигуры есть неотрицательное число; Ø Равные фигуры имеют равные площади; Ø Если фигура составлена из конечного числа фигур, не имеющих общих частей, то её площадь равна сумме площадей. Ø Существует фигура, площадь которой принимается за единицу. Как правило, за единицу площади принимается площадь квадрата со стороной, равной единичному отрезку е. Площадь такого квадрата обозначается е 2. Площадь - положительная величина, определенная на множестве плоских фигур так, что: üравные фигуры имеют равные площади; üесли фигура составлена из конечного числа фигур, то её площадь равна сумме их площадей.

Процесс измерения площади: 1) Выбирают единицу площади Е (обычно квадрат со стороной, равной единичному отрезку е). Е е 2) Сравнивают площадь фигуры с площадью единичного квадрата Е. 3) Результат сравнения обозначают числом и называют численным значением площади. SF = х. Е, где х — численное значение площади. Для нахождения численного значения площади фигур часто пользуются не измерением, а вычислением, что удобно, но для этого нужно знать формулы.

Задание. Вспомните формулы площади прямоугольника, квадрата, треугольника, круга и др. В начальной школе для измерения площади целесообразно использовать палетку (прозрачная пластина, разбитая на равные квадраты). Задание. Нарисуйте на листе бумаги в клетку любую замкнутую кривую без самопересечения. За единицу измерения площади примите площадь одной клетки. Измерьте площадь получившейся фигуры, используя формулу: S=n+k: 2, где n — количество клеток, целиком содержащихся во внутренней области фигуры, k — количество клеток, через которые проходит граница фигуры.

Некоторые свойства площадей 1. Если фигуры равны, то равны численные значения их площадей (при одной и той же единице площади). Обратное - неверно (в отличие от свойств длины). Фигуры, у которых площади равны, называют равновеликими. 2. Численное значение площади фигуры равно сумме численных значений площадей её составляющих частей (при одной и той же единице площади). 3. При замене единицы площади численное значение площади увеличивается (уменьшается) во столько раз, во сколько раз новая единица меньше (больше) старой. Пример: 7 дм 2 = 700 см 2, так как 1 см 2 = 0, 01 дм 2. Задание. Сформулируйте определение объема тела, процесса его измерения и свойства (по аналогии с площадью).

Масса тела Понятие о массе тела или вещества возникло из необходимости человека обменивать и продавать товары, продукты. Для измерения массы были придуманы рычажные весы и гири. Масса — одна из основных физических величин, которая связана с весом (силой, с которой тело давит на опору или оттягивает подвес в результате притяжения Земли). На различных широтах (например, на полюсе и на экваторе) вес одного и того же тела отличается. Масса же остается неизменной и является характеристикой только данного тела. С математической точки зрения: Масса - это положительная величина, определенная на множестве физических тел так, что: - масса одинакова у тел, уравновешивающих друга на весах; - массы складываются, когда тела соединяются вместе.

Весы получили свое название вследствие того, что на них измеряют вес предмета. Вес как сила измеряется в ньютонах и связан с массой формулой F=тg, в статичном положении отличается от неё только коэффициентом 9, 8 (ускорение свободного падения), что позволяет шкалу на весах сразу обозначить в килограммах, а не в ньютонах. Масса характеризуется теми же свойствами, что длина и площадь, только на множестве физических тел. Сравнение масс, действия над ними сводятся к сравнению и действиям над численными значениями масс. Процесс измерения массы 1. Выбирают тело, масса которого принимается за единицу (предполагается, что можно взять и её доли 0, 1; 0, 01 и т. д. ). 2. На одну чашу весов кладут измеряемое тело, а на другую - тела, выбранные в качестве единицы массы (гири) так, чтобы весы были уравновешены. 3. Считают численное значение массы гирь. Это и будет численным значением искомой массы. Задание. Решите задачу: «Имеются рычажные весы и 3 гири 8 кг, 5 кг, 3 кг. Как одним взвешиванием отмерить 6 кг крупы? »

Промежутки времени Понятие времени более сложное, чем понятие длины, площади, массы. Оно не имеет наглядности и познается опосредованно. Некоторые свойства промежутков времени 1. Промежутки времени можно сравнивать. ( «Красная Шапочка и Серый Волк» . ) 2. Промежутки времени можно складывать и вычитать. ( «Маша один час вырезала фигуры и один час их наклеивала. Сколько всего времени она затратила на работу? » ) 3. Промежутки времени можно умножать на число. ( « 7 суток — это неделя. Сколько суток в трех неделях? » ) 4. Промежутки времени можно измерять. Задание. Решите задачи. 1. Знаменитый греческий математик Архимед умер в 212 году до н. э. Сколько веков и сколько лет прошло с тех пор? 2. Четыре мальчика играли в футбол 2 часа. Сколько времени играл каждый мальчик?
Величины.pptx