Л4OTC.pptx
- Количество слайдов: 38

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Факультет фундаментальной подготовки Кафедра теоретических основ связи и радиотехники (ТОС и Р) располагается на 6 -м этаже В аудиториях № 607, № 609, № 611, 613. Дисциплина Общая теория связи Лектор: Заведующий кафедрой Шумаков Павел Петрович ОТС Лекция #4 1

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Лекция № 4 Спектрально-корреляционный анализ детерминированных сигналов в инфотелекоммуникации. 1. 2. 3. 4. Учебные вопросы: Энергетические модели сигналов. Корреляционные модели детерминированных сигналов. Свертка сигналов. Аналитический сигнал. ОТС Лекция #4 2

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Литература: Стр. 48. . 50; 53. . 54; 63. . 70 Используя Math. CAD расчитать и построить АКФ : 1) Интегрированием по определению АКФ. 2) ОПФ от энергетического спектра. Нечетные номера: треугольный и косинусоидальный. Четные номера : Прямоугольный и SINC-образный. ОТС Лекция #4 3
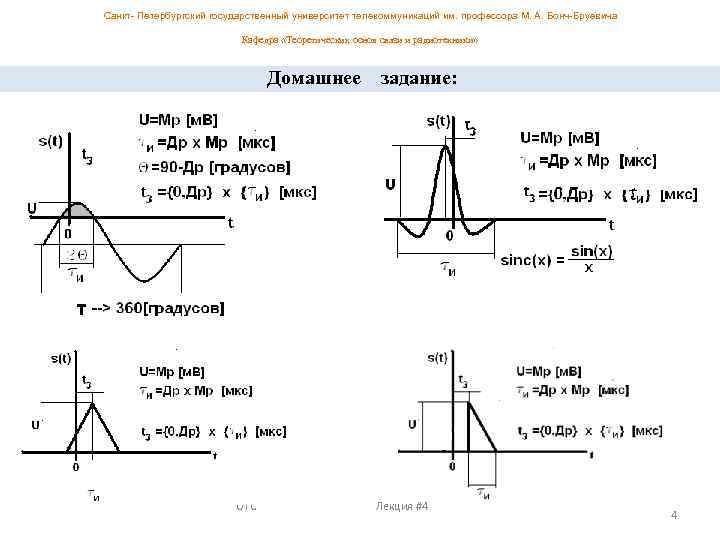
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Домашнее задание: ОТС Лекция #4 4
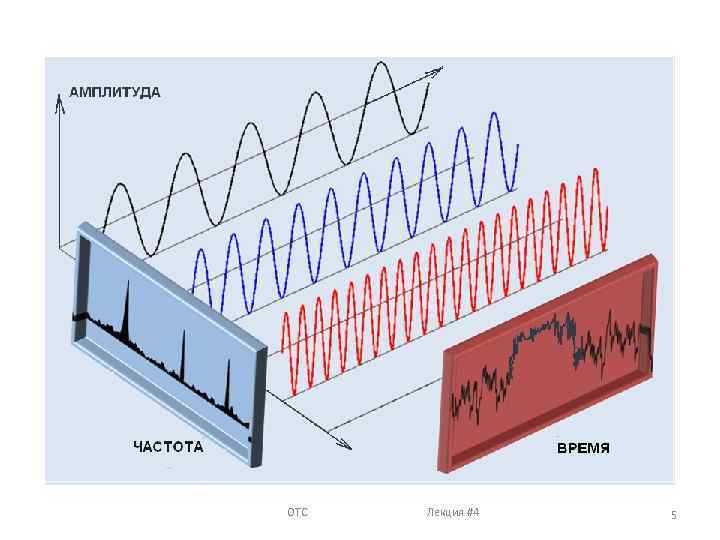
ОТС Лекция #4 5

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Спектры периодических сигналов. Формы спектрального представления периодического сигнала Квадратурная ОТС Лекция #4 6

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Амплитудно – фазовая форма ряда Фурье ОТС Лекция #4 7
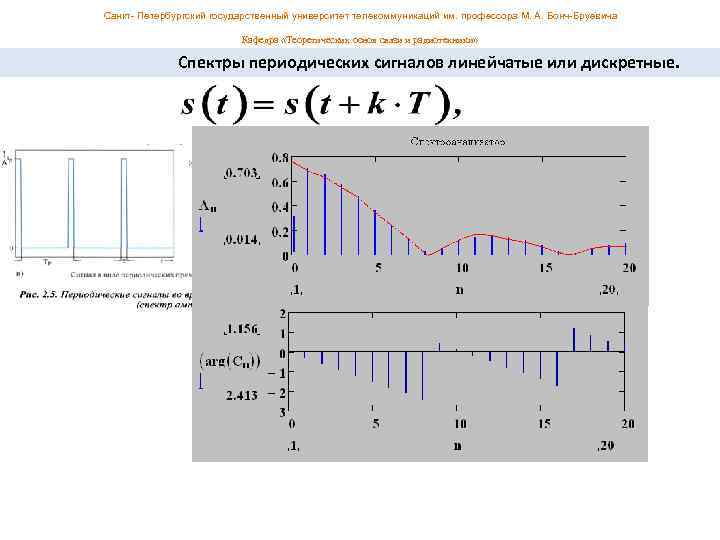
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Спектры периодических сигналов линейчатые или дискретные.

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Комплексная форма ряда Фурье АЧС –четная функция частоты (обладает симметрией в области положительных и отрицательных частот) ФЧС – нечетная функция (обладает центральной симметрией) ОТС Лекция #4 9

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Комплексная форма ряда Фурье АЧС –четная функция частоты (обладает симметрией в области положительных и отрицательных частот) ФЧС – нечетная функция (обладает центральной симметрией) ОТС Лекция #4 10

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Прямое и обратное преобразование Фурье Обратное преобразование Фурье для сигнала s(t) - операция синтеза, поскольку с ее помощью сигнал восстанавливается (синтезируется) из спектральных составляющих. Для восстановления сигнала надо знать информацию об АЧС и ФЧС. Прямое преобразование Фурье – операция анализа сигнала на основе определения его спектральных составляющих. ОТС Лекция #4 11

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Физический смысл спектральной плотности сигнала Учитывая чётность модуля S(ω) и нечётность фазы φ(ω), обратное преобразование Фурье можно записать следующим образом Спектральная плотность сигнала является комплексной амплитудой эквивалентной гармоники на соответствующей опорной частоте. Эквивалентная гармоника есть результат когерентного сложения бесконечно большого числа гармоник с бесконечно малыми амплитудами расположенными в бесконечно малом по частоте диапазоне в районе выбранной (опорной) частоты. ОТС Лекция #4 12
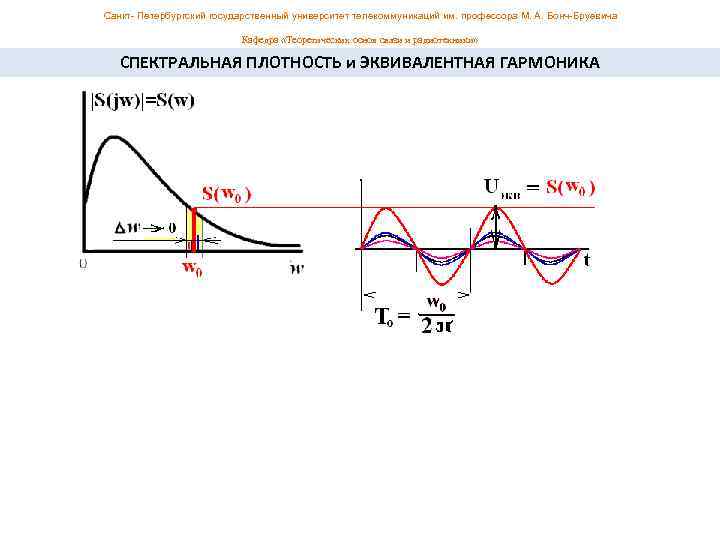
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ и ЭКВИВАЛЕНТНАЯ ГАРМОНИКА
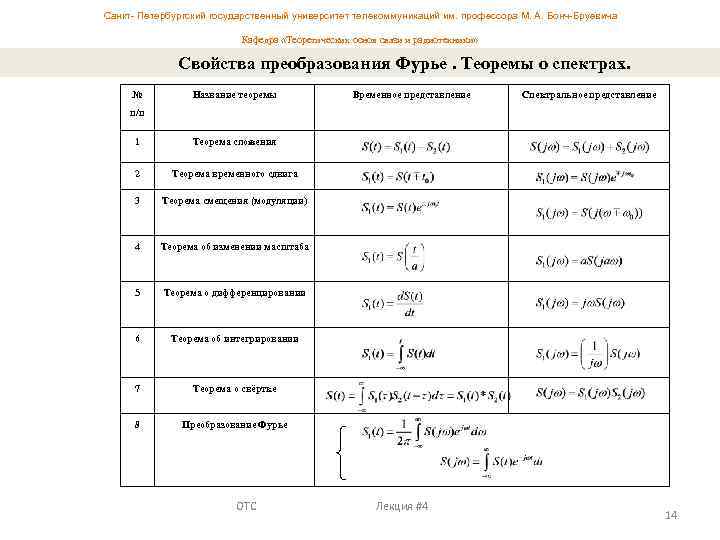
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Свойства преобразования Фурье. Теоремы о спектрах. № Название теоремы Временное представление Спектральное представление п/п 1 Теорема сложения 2 Теорема временного сдвига 3 Теорема смещения (модуляции) 4 Теорема об изменении масштаба 5 Теорема о дифференцировании 6 Теорема об интегрировании 7 Теорема о свёртке 8 Преобразование Фурье ОТС Лекция #4 14

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Теорема сложения спектров гласит: спектр суммы колебаний равен сумме спектров слагаемых колебаний. Теорема временного сдвига (запаздывания) формулируется следующим образом: при сдвиге колебания во времени (изменении начального момента отсчёта времени) спектральная плотность амплитуд сохраняется постоянной, а спектр фаз изменяется на величину, пропорциональную частоте и времени сдвига с учётом его знака. Теорема смещения (модуляции): умножение колебания S(t) на приводит к смещению его спектра на величину ω0. Теорема об изменении масштаба: растяжение колебания во времени (a>1) влечёт за собой сжатие его частотного спектра и увеличение спектральной плотности амплитуд. Сжатие колебания во времени (a<1) приводит к расширению его частотного спектра и уменьшению спектральной плотности амплитуд. Теорема о свёртке: свёртка двух колебаний S 1(t) и S 2(t) соответствует перемножению их спектров. ОТС Лекция #4 15

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Математический и Физический спектр непериодического сигнала Сопоставим комплексную и амплитудно фазовую формы ОПФ Учитывая чётность модуля S(ω) и нечётность фазы φ(ω), обратное преобразование Фурье можно записать следующим образом ОТС Лекция #4 16

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Вопрос 1. Энергетические модели сигналов. Основными энергетическими характеристиками вещественного сигнала s(t) являются его мощность и энергия. Мгновенная мощность определяется как квадрат мгновенного значения s(t): i(t) s(t) u(t) R=1 Энергия сигнала на интервале t 2, t 1 определяется как интеграл от мгновенной мощности: Средняя мощность сигнала s(t) на интервале t 2, t 1. ОТС Лекция #4 17

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Распределение энергии в спектре непериодического сигнала Рассмотрим выражение скалярного произведения в котором f(t)=g(t)=s(t), и = S(jω)↔ s(t) Равенства Парсеваля и обобщенная формула Рэлея. Энергетический спектр сигнала Распределение энергии в спектре вещественного непериодического сигнала ОТС Лекция #4 18
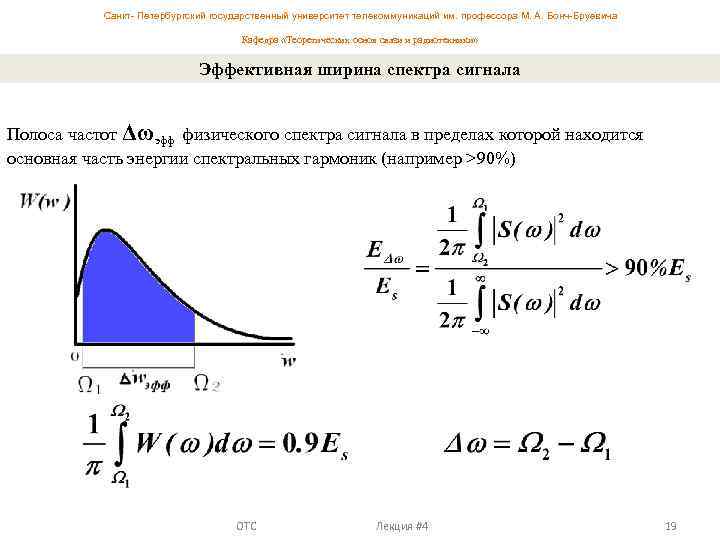
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Эффективная ширина спектра сигнала Полоса частот Δωэфф физического спектра сигнала в пределах которой находится основная часть энергии спектральных гармоник (например >90%) ОТС Лекция #4 19

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Вопрос№ 2. Корреляционные модели детерминированных сигналов Корреляция – количественная характеристика степени подобия (похожести) двух сигналов. Корреляционная функция – зависимость корреляции двух в общем случае комплексных сигналов от временного сдвига τ между ними. Для сигналов с ограниченной энергией. Для сигналов с конечной средней мощностью. Для периодических сигналов. ОТС Лекция #4 20

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Автокорреляционная функция вещественного сигнала (АКФ). Это корреляционная функция двух одинаковых сигналов - самого сигнала s(t) и его копии, задержанной во времени s(t-τ), рассматриваемая как функция времени задержки τ. Свойства АКФ вещественного сигнала R(τ). üАКФ определяет взаимную энергию сигнала и его копии, задержанной во времени и измеряется в Джоулях. üАКФ действительная и четная функция сдвига во времени τ : R(τ )=R(- τ ). График АКФ симметричен. üАКФ достигает максимума при τ=0 и максимальное значение АКФ равно ЭНЕРГИИ сигнала Еs. Поэтому R(0)=Es>R(τ ) ОТС Лекция #4 21

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Связь АКФ сигнала R(τ) с его энергетическим спектром W(ω). АКФ R(τ ) и энергетический спектр сигнала ОДНОЗНАЧНО связаны парой преобразований Фурье. Однозначно восстановить сигнал s(t ) по его АКФ R(τ ) невозможно, так как энергетический спектр W(ω), а значит и АКФ не содержат информацию о фазовом спектре сигнала. ОТС Лекция #4 22

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» АКФ периодического вещественного сигнала s(t+k. T). Это действительная периодическая корреляционная функция , измеряемая единицами средней мощности за период повторения (ВАТТЫ), четная по аргументу τ , максимумы повторяются через период повторения T. АКФ периодического сигнала связана с его линейчатым спектром через ряд Фурье: Примеры: ОТС Лекция #4 23

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Вопрос 3. Свертка сигналов Сигнал на выходе линейной системы ННУ ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА δ(t) s(t) ЛС (фильтр) g(t) y(t)=s(t) g(t) СВЕРТКА Частотная характеристика линейной системы ОТС Лекция #4 24
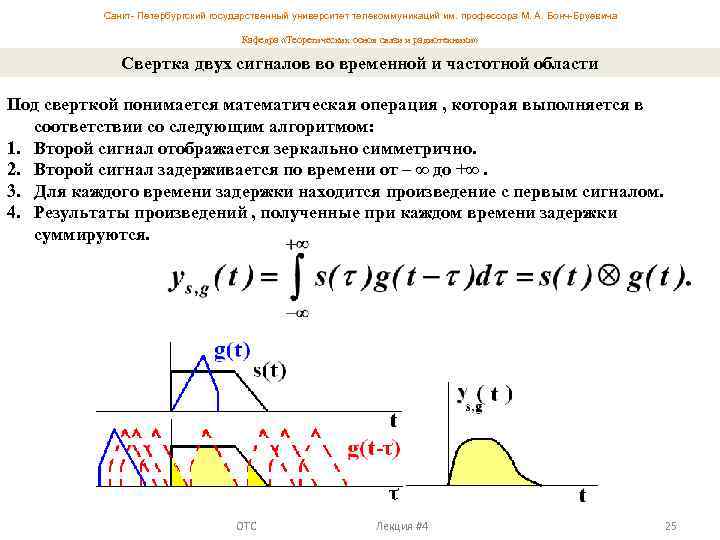
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Свертка двух сигналов во временной и частотной области Под сверткой понимается математическая операция , которая выполняется в соответствии со следующим алгоритмом: 1. Второй сигнал отображается зеркально симметрично. 2. Второй сигнал задерживается по времени от – ∞ до +∞. 3. Для каждого времени задержки находится произведение с первым сигналом. 4. Результаты произведений , полученные при каждом времени задержки суммируются. ОТС Лекция #4 25

Свойства свертки коммутативность дистрибутивность ассоциативность ОТС Лекция #4 26
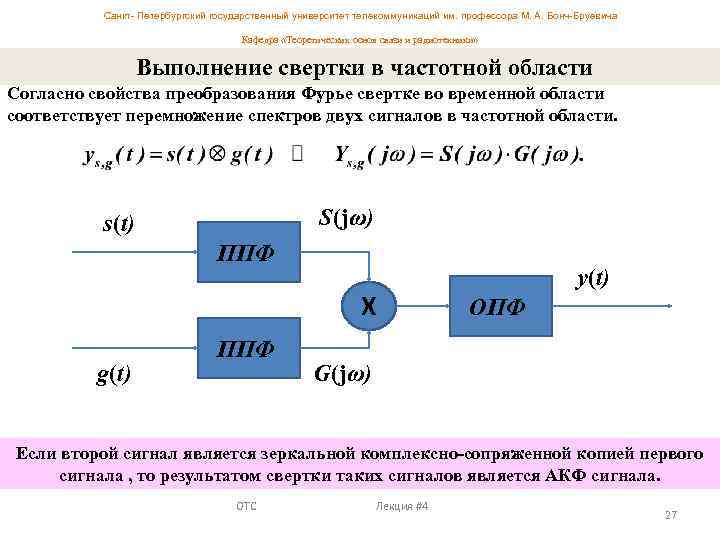
Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» Выполнение свертки в частотной области Согласно свойства преобразования Фурье свертке во временной области соответствует перемножение спектров двух сигналов в частотной области. S(jω) s(t) ППФ X g(t) ППФ y(t) ОПФ G(jω) Если второй сигнал является зеркальной комплексно-сопряженной копией первого сигнала , то результатом свертки таких сигналов является АКФ сигнала. ОТС Лекция #4 27
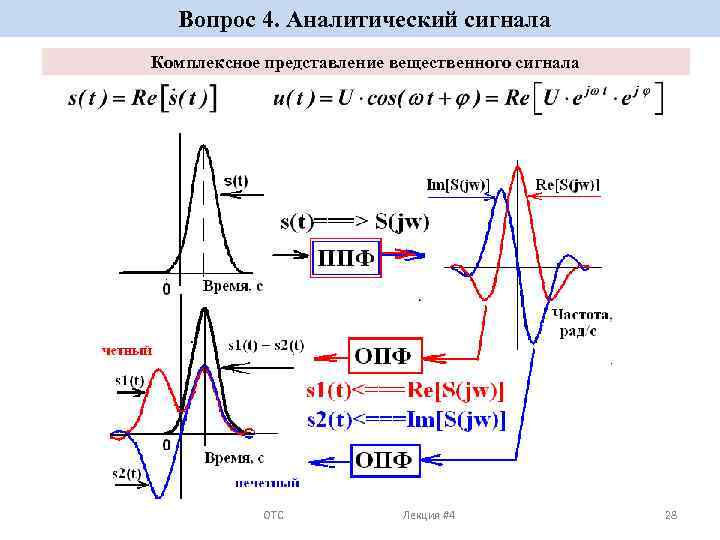
Вопрос 4. Аналитический сигнала Комплексное представление вещественного сигнала ОТС Лекция #4 28
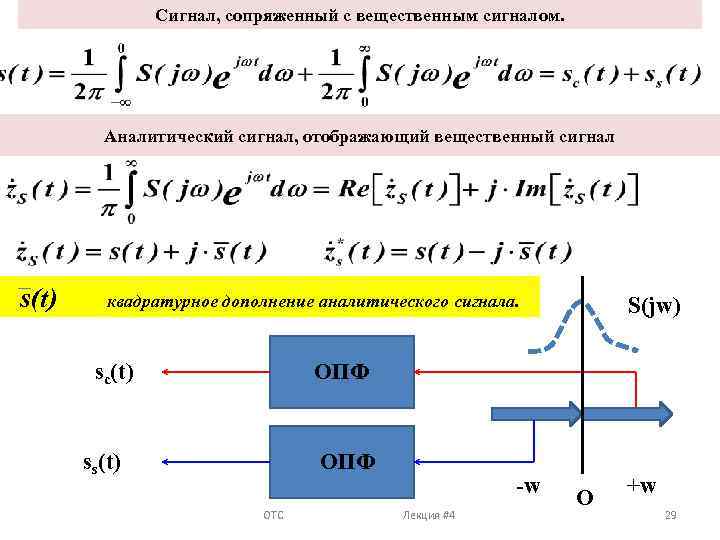
Сигнал, сопряженный с вещественным сигналом. Аналитический сигнал, отображающий вещественный сигнал s(t) квадратурное дополнение аналитического сигнала. sc(t) ss(t) S(jw) ОПФ ОТС Лекция #4 -w О +w 29
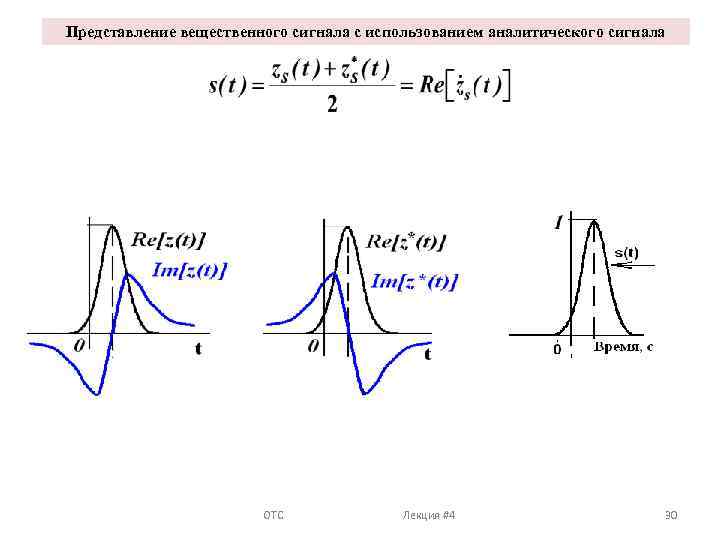
Представление вещественного сигнала с использованием аналитического сигнала ОТС Лекция #4 30

Преобразование Гильберта Реальная и мнимая части спектра произвольных каузальных сигналов связаны преобразованием Гильберта. Вещественный сигнал и его квадратурное дополнение связаны преобразованием Гильберта Преобразование Гильберта есть свертка сигнала и ядра ОТС Лекция #4 1/πt 31
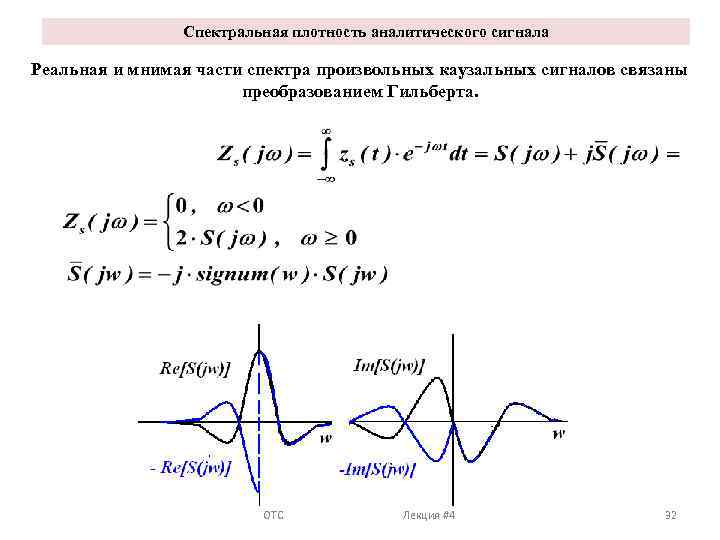
Спектральная плотность аналитического сигнала Реальная и мнимая части спектра произвольных каузальных сигналов связаны преобразованием Гильберта. ОТС Лекция #4 32

Санкт- Петербургский государственный университет телекоммуникаций им. профессора М. А. Бонч-Бруевича Кафедра «Теоретических основ связи и радиотехники» ОТС Лекция #4 33

Линейная Дискретная свертка (свертка дискретных сигналов) Длина первого N отсчетов, длина второго M отсчетов Круговая (циклическая )Дискретная свертка Обе последовательности имеют одинаковую длину N отсчетов Чтобы выровнять длину последовательностей их дополняют нулями до длины M+N-1. ОТС Лекция #4 34
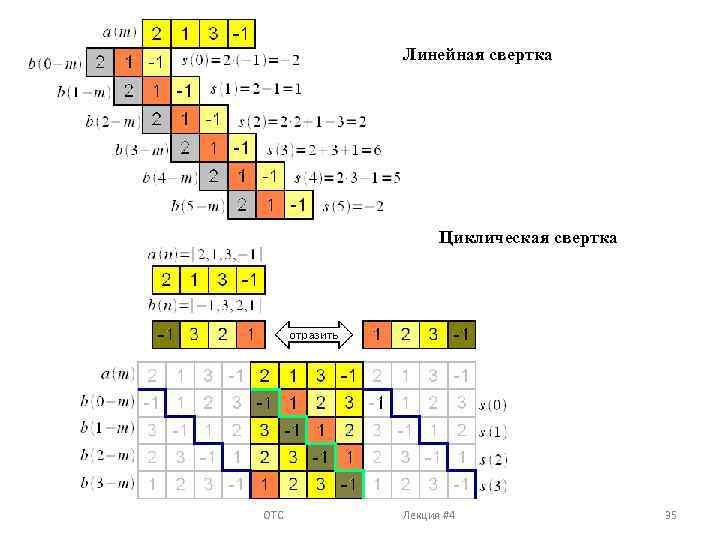
Линейная свертка Циклическая свертка ОТС Лекция #4 35
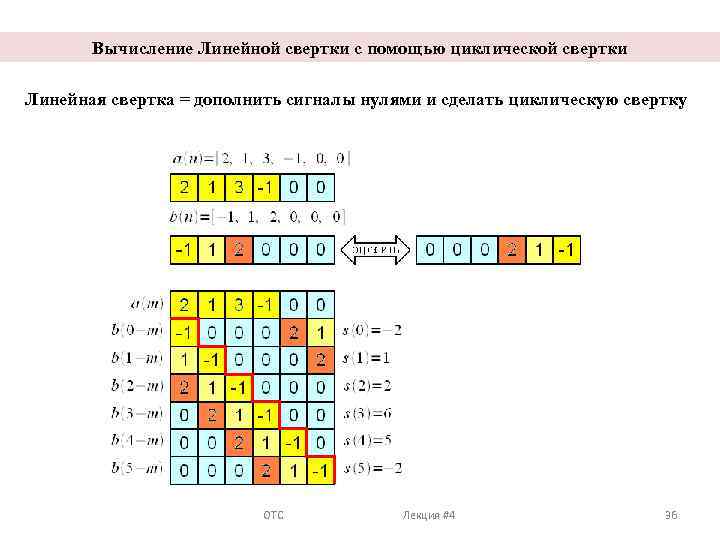
Вычисление Линейной свертки с помощью циклической свертки Линейная свертка = дополнить сигналы нулями и сделать циклическую свертку ОТС Лекция #4 36

Дискретное преобразование Фурье Аналогично можно поступить и при расчете линейной свертки через циклическую. Рассмотрим пример. Пусть , а . Прямое вычисление линейной свертки потребует (12 миллионов) операций умножения и сложения. Дополним каждую из последовательностей до 8192 отсчетов нулями и применим алгоритм БПФ с прореживание по времени, тогда на вычисление одного БПФ потребуется операций комплексного умножения или 428000 операций действительного умножения. Таких блоков БПФ будет всего 3 штуки, плюс надо учесть 8192 комплексных умножений спектров, итого , что почти в 7. 5 раз ниже чем если бы мы считали линейную свертку в лоб ОТС Лекция #4 37
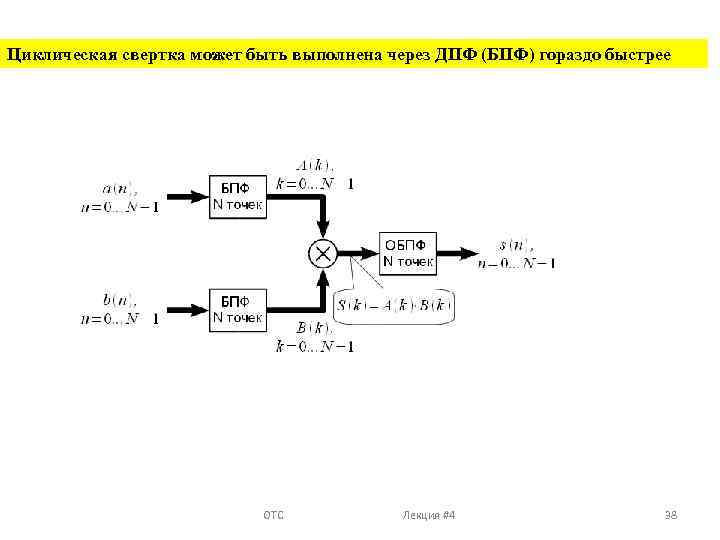
Циклическая свертка может быть выполнена через ДПФ (БПФ) гораздо быстрее ОТС Лекция #4 38
Л4OTC.pptx