Sampling Techniques for Probabilistic Roadmap Planners Roland Geraerts and Mark Overmars IAS-8 March 2004
Overview n n n Probabilistic roadmaps Test scenes PRM choices Sampling Variation of running times Conclusions
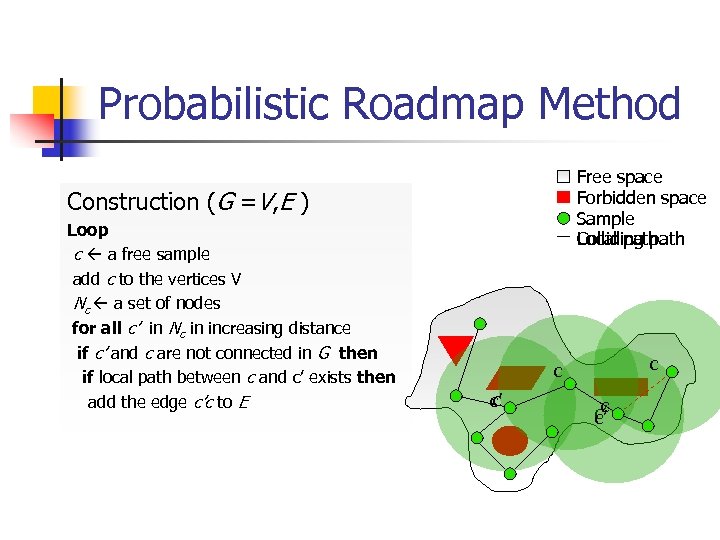
Probabilistic Roadmap Method Free space Forbidden space Sample Local path Colliding path Construction (G =V, E ) Loop c a free sample add c to the vertices V Nc a set of nodes for all c’ in Nc in increasing distance if c’ and c are not connected in G then if local path between c and c’ exists then add the edge c’c to E c c’ c’
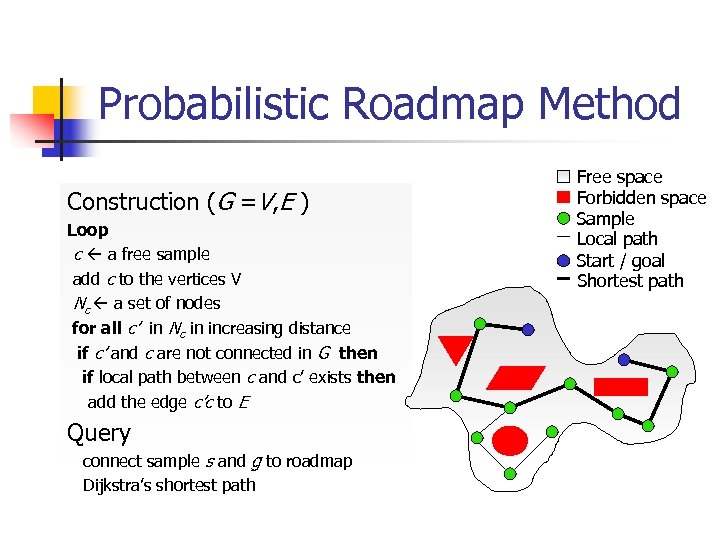
Probabilistic Roadmap Method Construction (G =V, E ) Loop c a free sample add c to the vertices V Nc a set of nodes for all c’ in Nc in increasing distance if c’ and c are not connected in G then if local path between c and c’ exists then add the edge c’c to E Query connect sample s and g to roadmap Dijkstra’s shortest path Free space Forbidden space Sample Local path Start / goal Shortest path
Test Scenes n Comparison of techniques
Experimental Setup n Environment n Single system n n Same computer n n Cage, clutter, hole, house, rooms, wrench Preprocessing method n n Pentium IV 2. 66 GHz, 1 GB memory Same test scenes n n SAMPLE but single query Average time (s) over 30 runs
PRM choices n Collision checking on local path n n Incremental Binary Rotate-at-s Neighbor selecting n n n Nearest-k Component-k Visibility
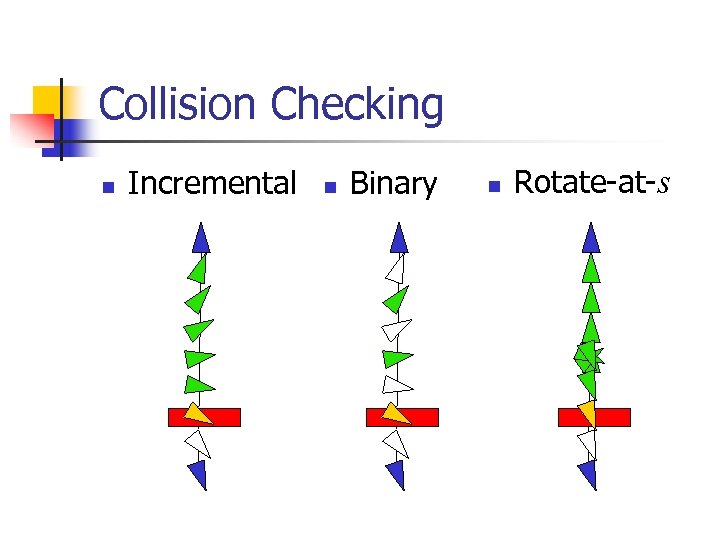
Collision Checking n Incremental n Binary n Rotate-at-s
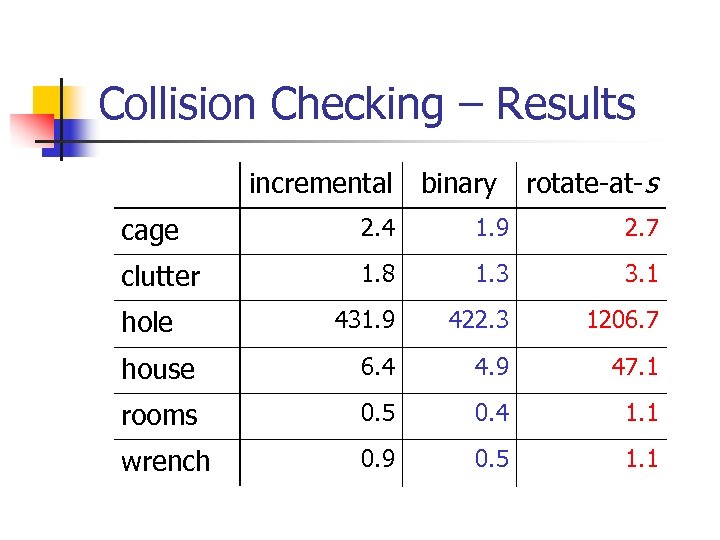
Collision Checking – Results incremental binary rotate-at-s cage 2. 4 1. 9 2. 7 clutter 1. 8 1. 3 3. 1 431. 9 422. 3 1206. 7 house 6. 4 4. 9 47. 1 rooms 0. 5 0. 4 1. 1 wrench 0. 9 0. 5 1. 1 hole
Neighbor Strategy n Nearest-k n n Component n n Nearest 1 neighbor in each connected component Component-k n n Nearest k neighbors in each connected component Visibility n Only useful nodes, add node/connection only if: n n Node cannot be connected to other nodes Node can be connected to 2 (or more) connected components
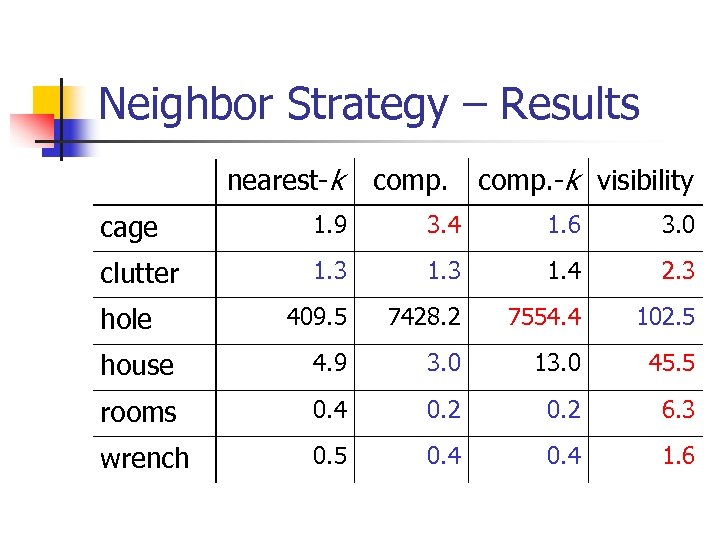
Neighbor Strategy – Results nearest-k comp. -k visibility cage 1. 9 3. 4 1. 6 3. 0 clutter 1. 3 1. 4 2. 3 409. 5 7428. 2 7554. 4 102. 5 house 4. 9 3. 0 13. 0 45. 5 rooms 0. 4 0. 2 6. 3 wrench 0. 5 0. 4 1. 6 hole
Uniform Sampling n Random n Grid
Uniform Sampling n Cell n Halton (variants)
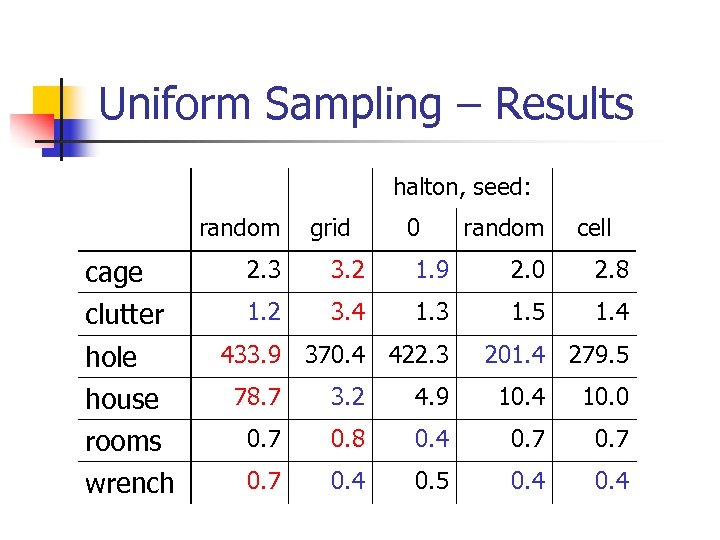
Uniform Sampling – Results halton, seed: random cage clutter hole house rooms wrench grid 0 random cell 2. 3 3. 2 1. 9 2. 0 2. 8 1. 2 3. 4 1. 3 1. 5 1. 4 433. 9 370. 4 422. 3 201. 4 279. 5 78. 7 3. 2 4. 9 10. 4 10. 0 0. 7 0. 8 0. 4 0. 7 0. 4 0. 5 0. 4
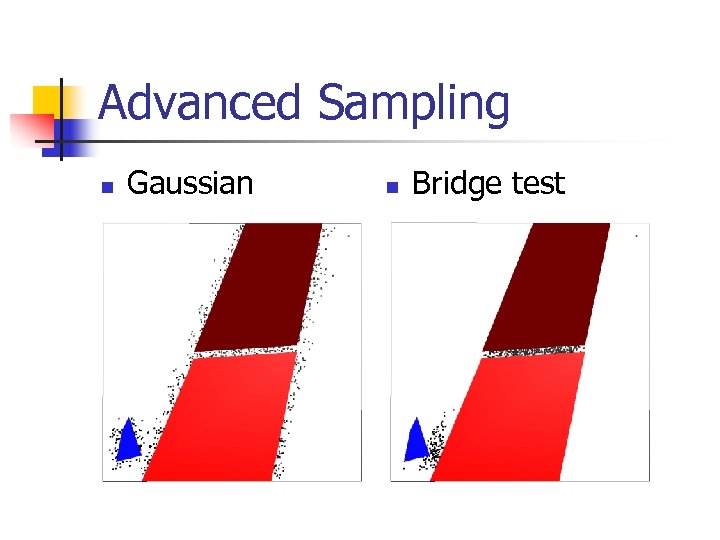
Advanced Sampling n Gaussian n Bridge test
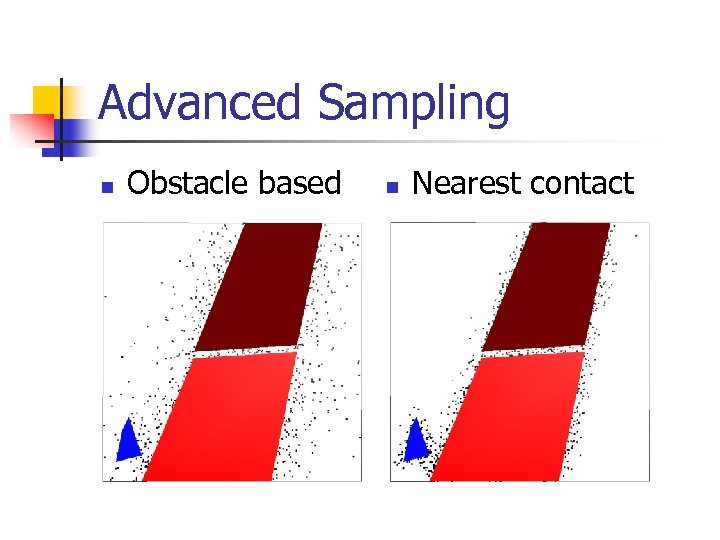
Advanced Sampling n Obstacle based n Nearest contact
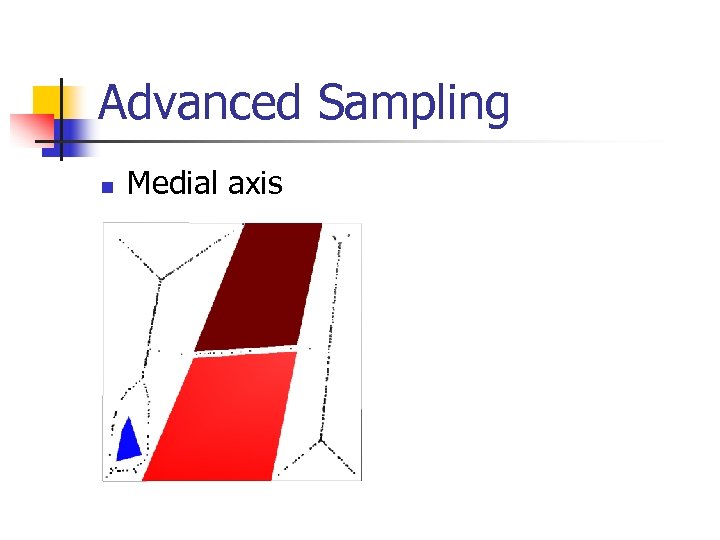
Advanced Sampling n Medial axis
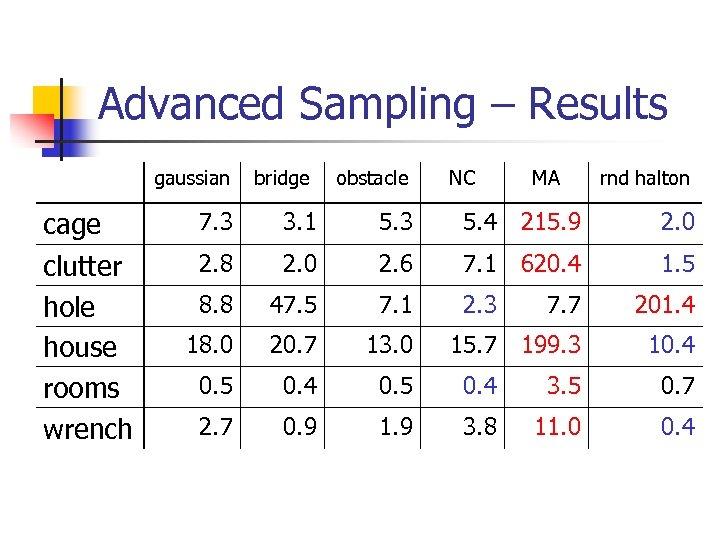
Advanced Sampling – Results gaussian cage clutter hole house rooms wrench bridge obstacle NC MA rnd halton 7. 3 3. 1 5. 3 5. 4 215. 9 2. 0 2. 8 2. 0 2. 6 7. 1 620. 4 1. 5 8. 8 47. 5 7. 1 2. 3 7. 7 201. 4 18. 0 20. 7 13. 0 15. 7 199. 3 10. 4 0. 5 0. 4 3. 5 0. 7 2. 7 0. 9 1. 9 3. 8 11. 0 0. 4
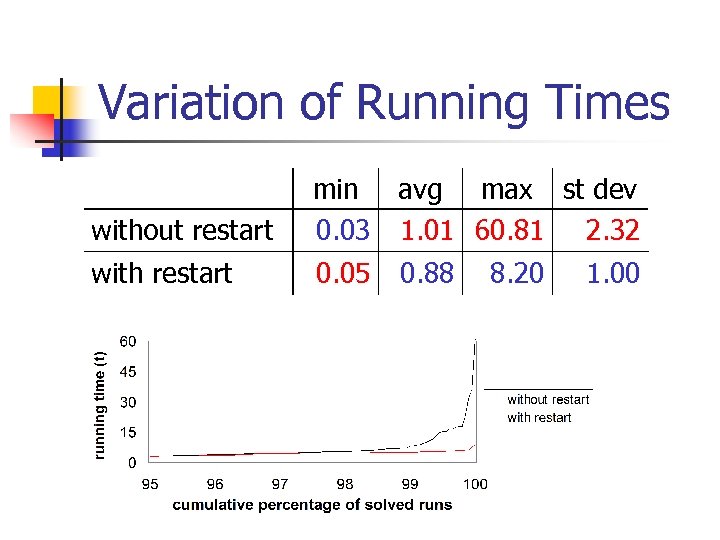
Variation of Running Times without restart min avg max st dev 0. 03 1. 01 60. 81 2. 32 with restart 0. 05 0. 88 8. 20 1. 00
Conclusions n n Many claims could not be confirmed Local planner n n Rotate-at-s is worse than binary collision checking Node adding n n Component-k seems to work best Visibility sampling didn’t perform as well as expected
Conclusions n Sampling n n n Small difference between uniform methods Halton didn’t outperform uniform sampling but may be preferred (deterministic) Advanced sampling is only useful in scenes with large open areas and some narrow passages It is not necessarily true that a combination of good techniques is good Reduction of variance is desirable
Questions n n Home page: www. cs. uu. nl/~roland Mail: roland@cs. uu. nl
Скачать презентацию Sampling Techniques for Probabilistic Roadmap Planners Roland Geraerts
286c6bcb7aa078d1b2d01ae7314754bf.ppt