9f37497d32654327c8989e1048a5f1a8.ppt
- Количество слайдов: 49

SAHGA – Um algoritmo genético híbrido com representação explícita de relacionamentos espaciais para análise de dados geoespaciais Tese de doutorado em Computação Aplicada Adair Santa Catarina Orientadores: Dr. Antônio Miguel Vieira Monteiro Dr. João Ricardo de Freitas Oliveira INPE – Abr/2009

Roteiro n Introdução n Referencial Teórico: ¨ Representação do espaço bi-dimensional e vizinhança espacial; ¨ Algoritmos Genéticos; ¨ Model Breeders; ¨ Species Distribution Models. n SAHGA Model Breeder n SAHGA SDM n Conclusões n Referências Bibliográficas 2
Introdução Informações ão aç ut p om c GIS eo G Dados Organizados 3
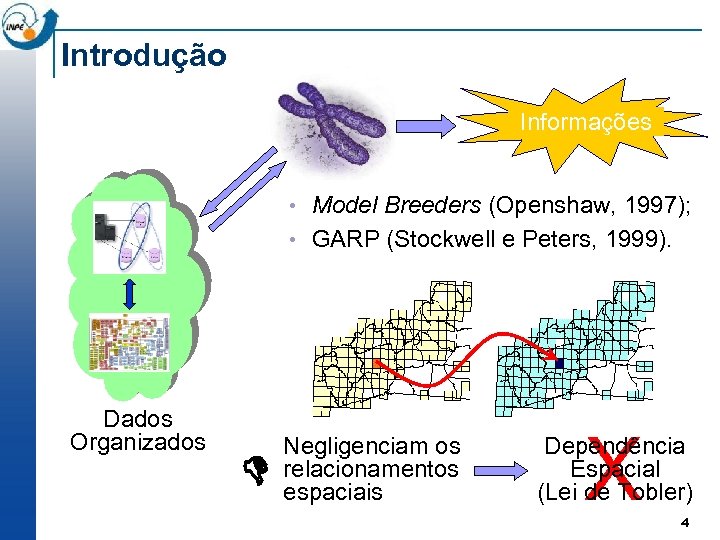
Introdução Informações • Model Breeders (Openshaw, 1997); • GARP (Stockwell e Peters, 1999). Dados Organizados D Negligenciam os relacionamentos espaciais X Dependência Espacial (Lei de Tobler) 4

Questões n n É possível incorporar os relacionamentos espaciais em sistemas semi-automáticos de análise de dados geoespaciais baseados em AG? Estes sistemas são capazes de operar sobre um modelo generalizado de relacionamentos espaciais? Os relacionamentos espaciais afetam os resultados fornecidos por tais sistemas? O conhecimento pré-existente, acerca dos fatores ambientais que afetam o problema em estudo, pode ser representado nestes sistemas? 5

Hipótese Central n É possível incorporar aos AG, utilizados em sistemas de análise de dados geoespaciais, uma estrutura para representação explícita de relacionamentos espaciais, a GPM – Generalized Proximity Matrix, possibilitando-os considerar os efeitos da dependência espacial nos fenômenos estudados. n Verificação da hipótese prova de conceito ¨ SAHGA – Spatially Aware Hybrid Genetic Algorithm n n SAHGA MB dados sócio-econômicos SAHGA SDM duas espécies de aves 6

Roteiro n Introdução n Referencial Teórico: ¨ Representação do espaço bi-dimensional e vizinhança espacial; ¨ Algoritmos Genéticos; ¨ Model Breeders; ¨ Species Distribution Models. n SAHGA Model Breeder n SAHGA SDM n Conclusões n Referências Bibliográficas 7

Representação do Espaço 2 D n Polígonos ou grades regulares: 8

Generalized Proximity Matrix (GPM) n n Aguiar et al. , 2003. Estrutura da GPM: ¨ Conjunto de objetos O: n n ¨ Grafo (G): n n ¨ Células regulares; Polígonos. Nós = objetos; Arcos = relacionamentos. Matriz de proximidade (V): n n Conjunto de valores Wij que indicam o quanto dois objetos Oi e Oj estão relacionados; Wij relacionamentos no espaço absoluto ou relativo. 9
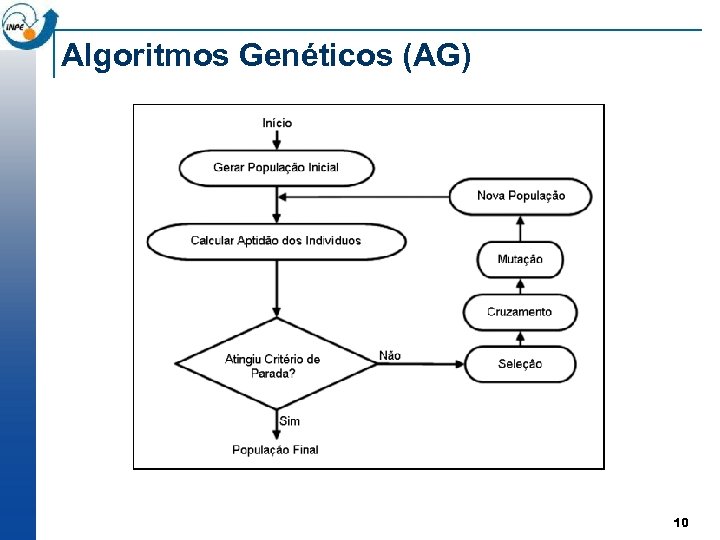
Algoritmos Genéticos (AG) 10

Simulated Annealing n Metropolis (1953); Kirkpatrick et al. (1983): gi e gj = níveis energéticos; ck = temperatura. n n Extensão do método de busca local; Habilidade para fugir da armadilha do ótimo local. 11

Model Breeders n Openshaw & Openshaw (1997), Santa Catarina et al. (2005): y = f(x 1, x 2, . . . , xn); n n n Núcleo de otimização utilizam AG; Vantagens: modelos simples de compreender e eficiência computacional; Desvantagem: simplificação do fenômeno observado e grande consumo de tempo para resposta ótima. 12
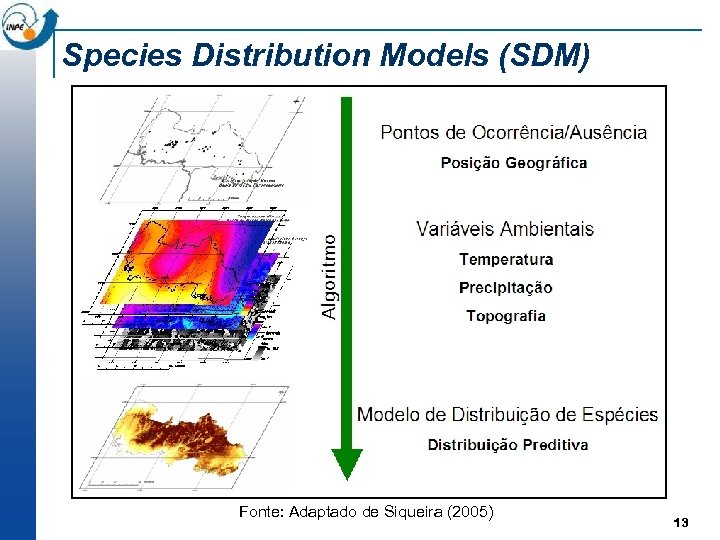
Species Distribution Models (SDM) Fonte: Adaptado de Siqueira (2005) 13
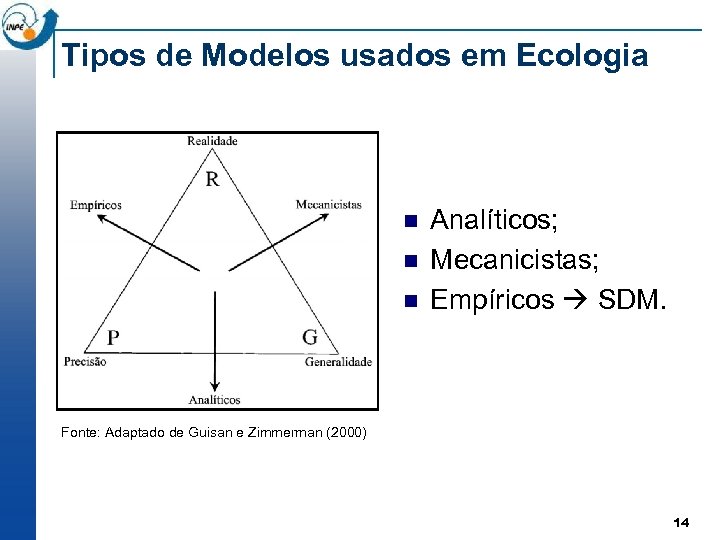
Tipos de Modelos usados em Ecologia n n n Analíticos; Mecanicistas; Empíricos SDM. Fonte: Adaptado de Guisan e Zimmerman (2000) 14
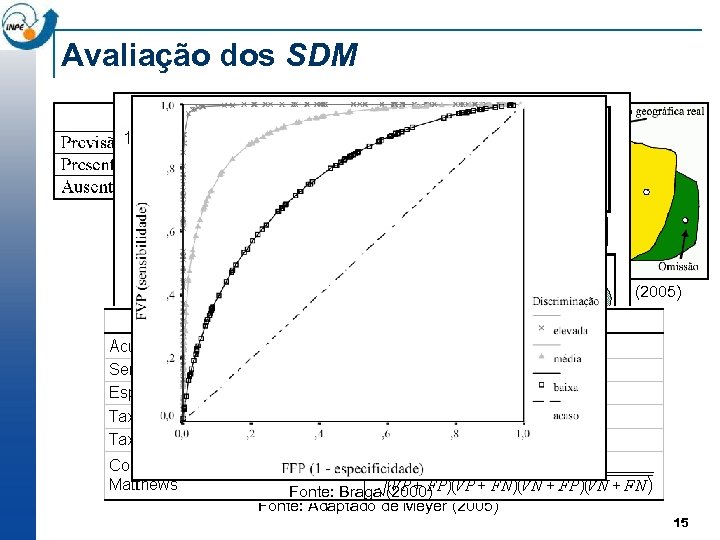
Avaliação dos SDM Matriz de Confusão Fonte: Adaptado de Siqueira (2005) Fonte: Braga (2000) Fonte: Adaptado de Meyer (2005) 15

Roteiro n Introdução n Referencial Teórico: ¨ Representação do espaço bi-dimensional e vizinhança espacial; ¨ Algoritmos Genéticos; ¨ Model Breeders; ¨ Species Distribution Models. n SAHGA Model Breeder n SAHGA SDM n Conclusões n Referências Bibliográficas 16
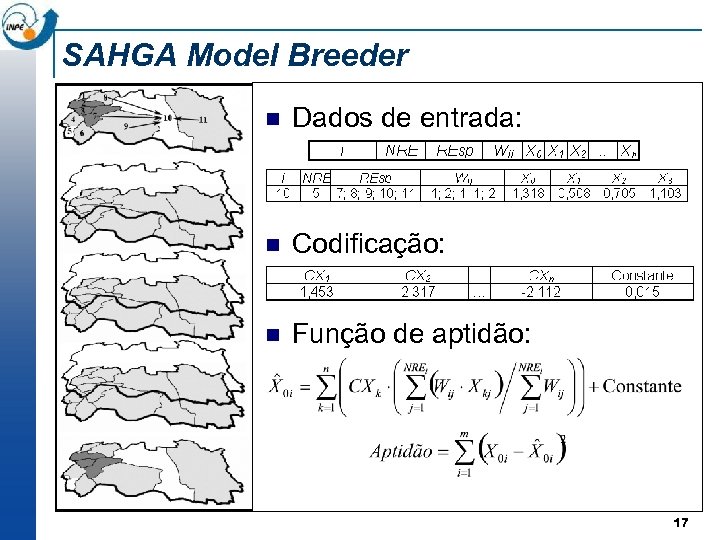
SAHGA Model Breeder n Dados de entrada: n Codificação: n Função de aptidão: 17

Núcleo de Otimização – SAHGA 18

Operadores Genéticos – SAHGA n n Seleção pelo método da roleta; Cruzamento aritmético de Michalewicz (1996): n Mutação uniforme [-4; 4]; Busca local (SA) mutação uniforme [-0, 5; 0, 5]; Elitismo. n Padronização das variáveis de entrada: n n 19
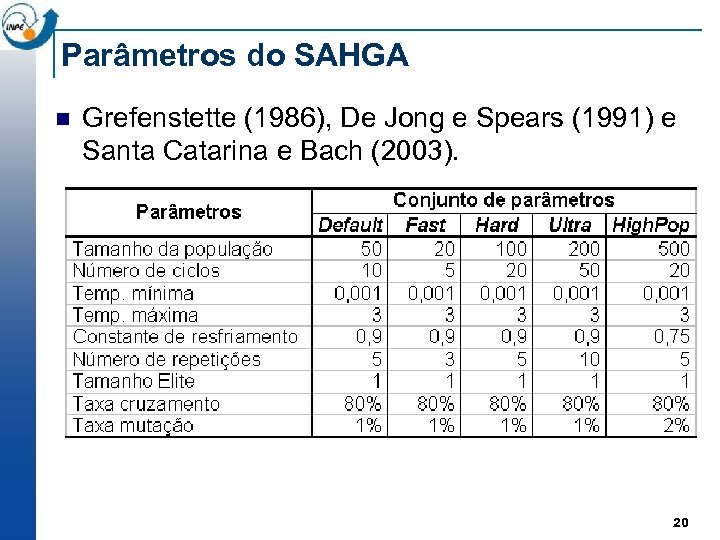
Parâmetros do SAHGA n Grefenstette (1986), De Jong e Spears (1991) e Santa Catarina e Bach (2003). 20
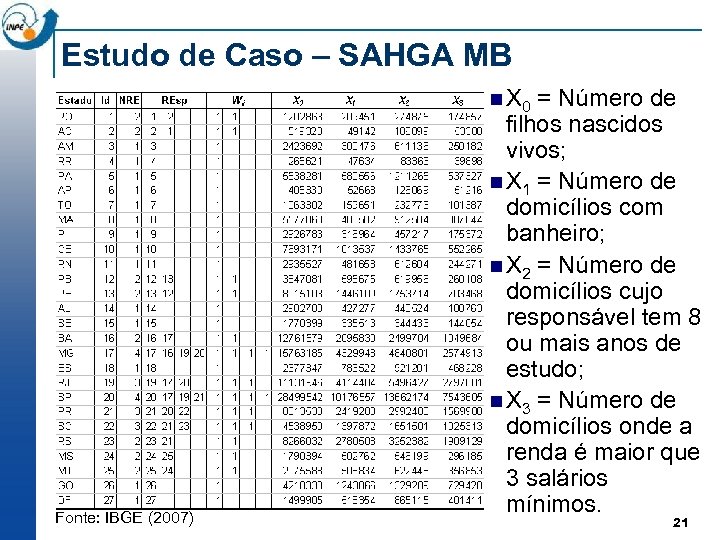
Estudo de Caso – SAHGA MB n X 0 Fonte: IBGE (2007) = Número de filhos nascidos vivos; n X 1 = Número de domicílios com banheiro; n X 2 = Número de domicílios cujo responsável tem 8 ou mais anos de estudo; n X 3 = Número de domicílios onde a renda é maior que 3 salários mínimos. 21

Modelos Ajustados – SAHGA MB n Configuração dos parâmetros = Default n Desconsiderando a GPM: Cada estado está relacionado apenas consigo mesmo Wii = 1 Aptidão mínima = 0, 9298. n Considerando a GPM: Aptidão mínima = 1, 0737. 22
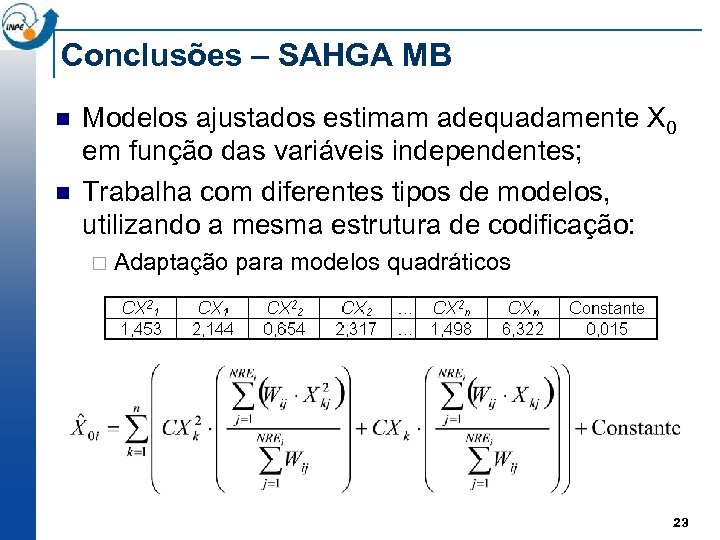
Conclusões – SAHGA MB n n Modelos ajustados estimam adequadamente X 0 em função das variáveis independentes; Trabalha com diferentes tipos de modelos, utilizando a mesma estrutura de codificação: ¨ Adaptação para modelos quadráticos 23

Roteiro n Introdução n Referencial Teórico: ¨ Representação do espaço bi-dimensional e vizinhança espacial; ¨ Algoritmos Genéticos; ¨ Model Breeders; ¨ Species Distribution Models. n SAHGA Model Breeder n SAHGA SDM n Conclusões n Referências Bibliográficas 24
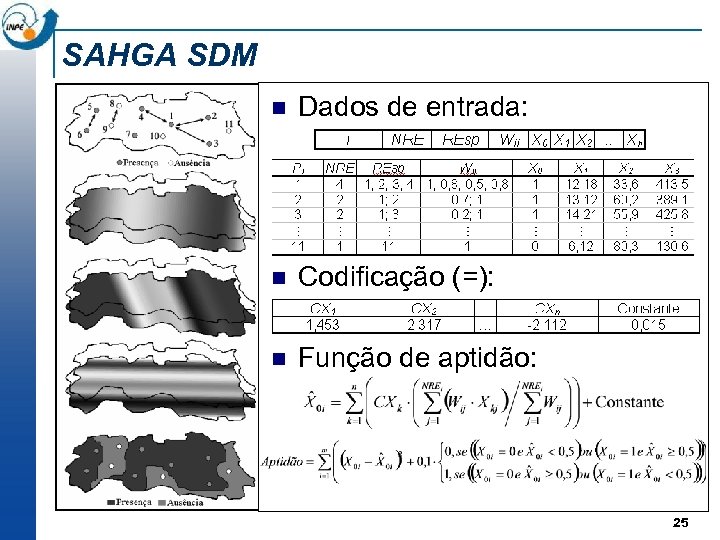
SAHGA SDM n Dados de entrada: n Codificação (=): n Função de aptidão: 25

Estudos de Caso – SAHGA SDM n Distribuição potencial de duas espécies de aves: Strix varia Thalurania furcata boliviana 26
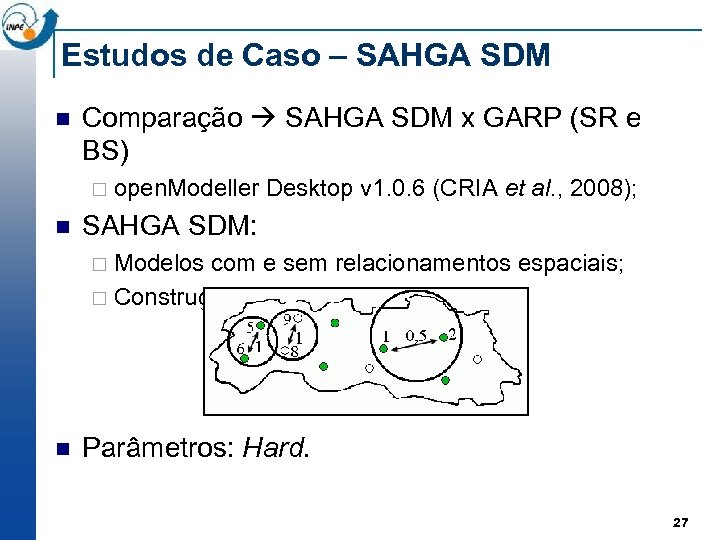
Estudos de Caso – SAHGA SDM n Comparação SAHGA SDM x GARP (SR e BS) ¨ n open. Modeller Desktop v 1. 0. 6 (CRIA et al. , 2008); SAHGA SDM: Modelos com e sem relacionamentos espaciais; ¨ Construção da GPM: ¨ n Parâmetros: Hard. 27

Espécie Strix varia n Dados: Base exemplo do Desktop. Garp (Kansas University, 2007); ¨ 1218 pontos de presença 100 selecionados; ¨ 7 layers geográficos: temperatura, precipitação e relevo; ¨ 100 pontos de pseudo-ausência modelo Bio. Clim (Nix, 1986) open. Modeller Desktop; ¨ Treino (50%) e teste (50%); ¨ GPM raio de 100 km. ¨ 28
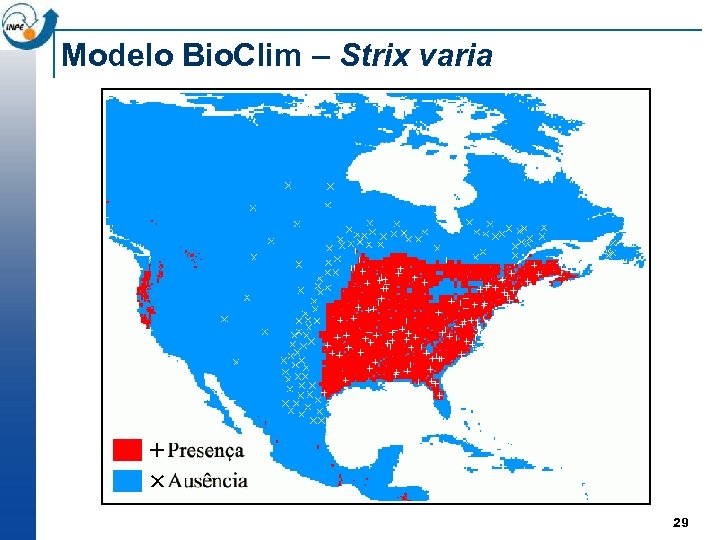
Modelo Bio. Clim – Strix varia 29
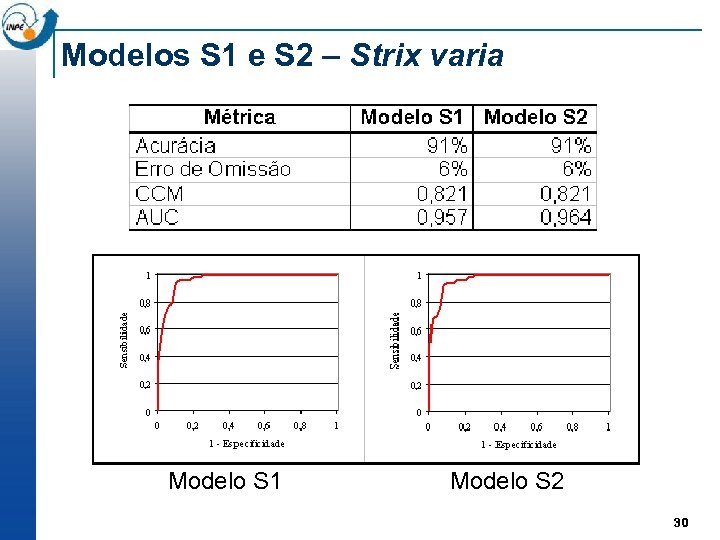
Modelos S 1 e S 2 – Strix varia Modelo S 1 Modelo S 2 30
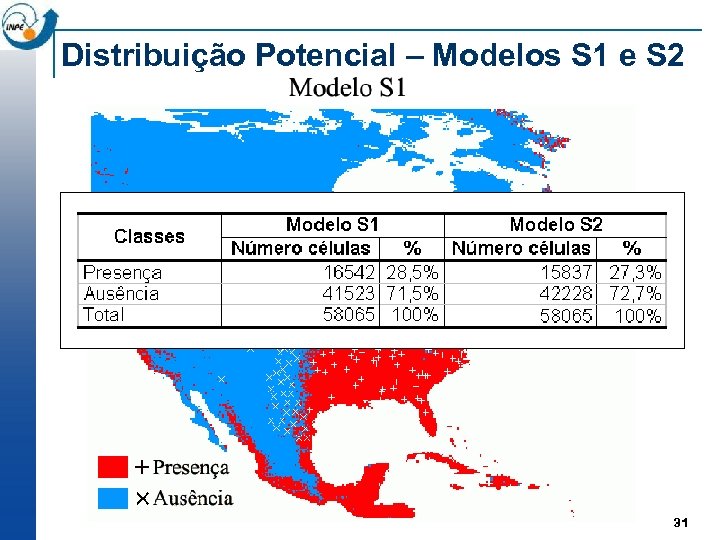
Distribuição Potencial – Modelos S 1 e S 2 31
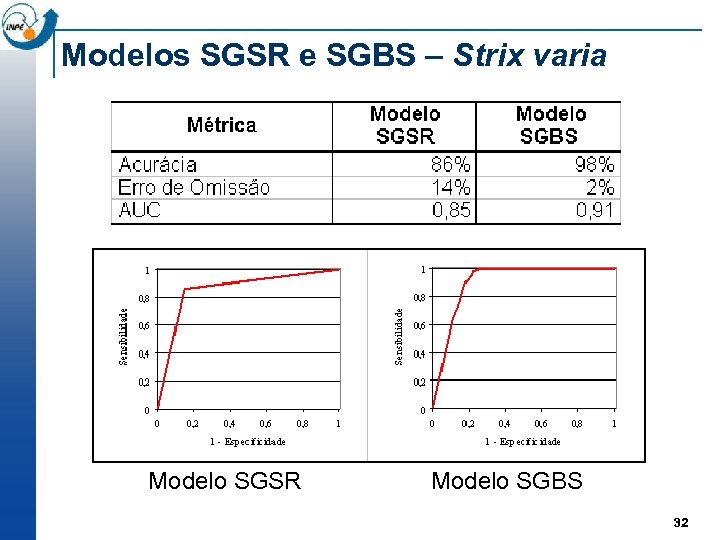
Modelos SGSR e SGBS – Strix varia Modelo SGSR Modelo SGBS 32
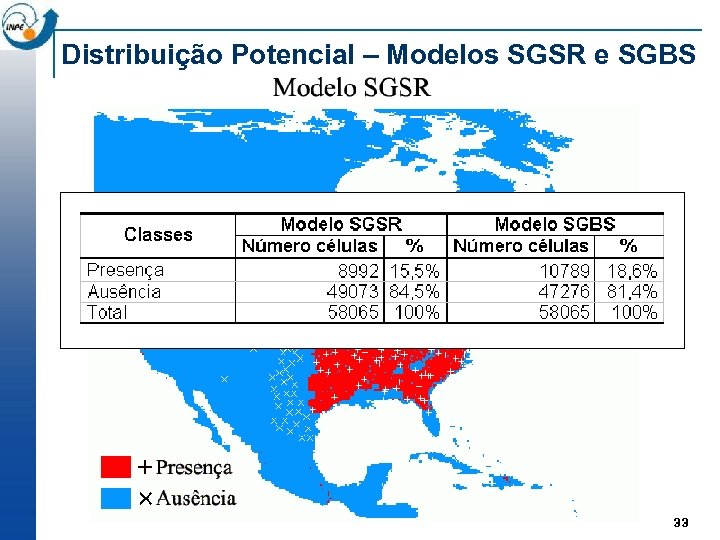
Distribuição Potencial – Modelos SGSR e SGBS 33

Espécie Thalurania furcata boliviana n Dados: Base exemplo do open. Modeller Desktop; ¨ 65 pontos de presença; ¨ 8 layers geográficos: precipitação e temperatura; ¨ 50 pontos de pseudo-ausência modelo Bio. Clim open. Modeller Desktop; ¨ Treino (40 P/30 A) e teste (25 P/20 A); ¨ GPM raio de 100 km. ¨ 34
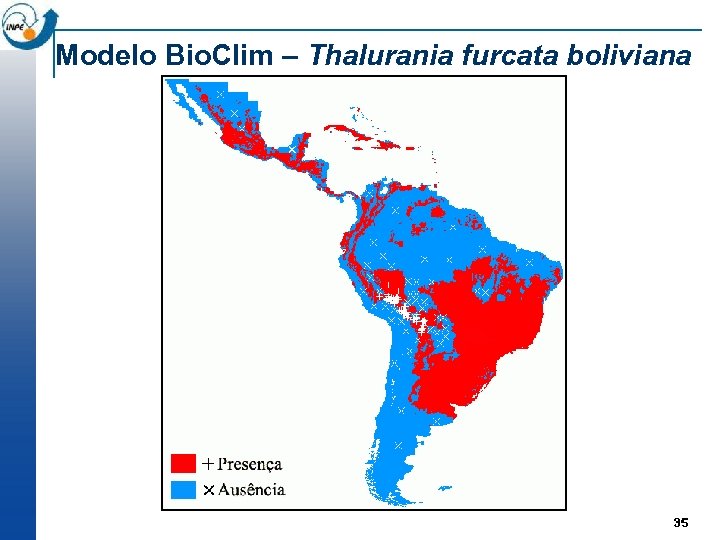
Modelo Bio. Clim – Thalurania furcata boliviana 35
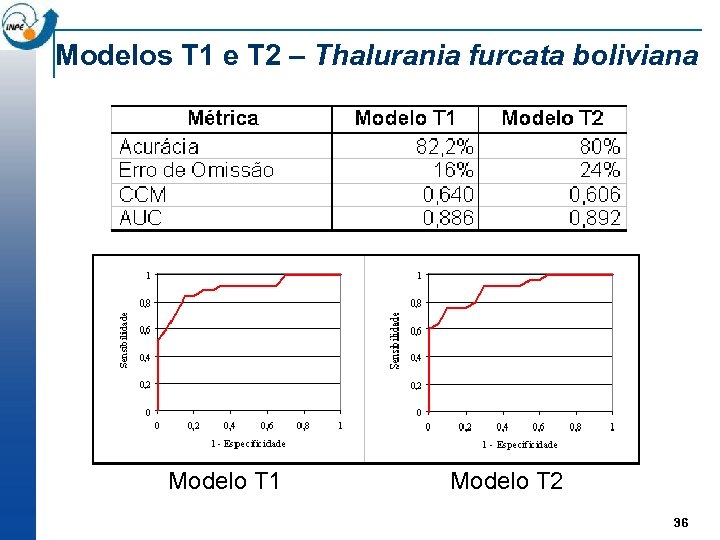
Modelos T 1 e T 2 – Thalurania furcata boliviana Modelo T 1 Modelo T 2 36
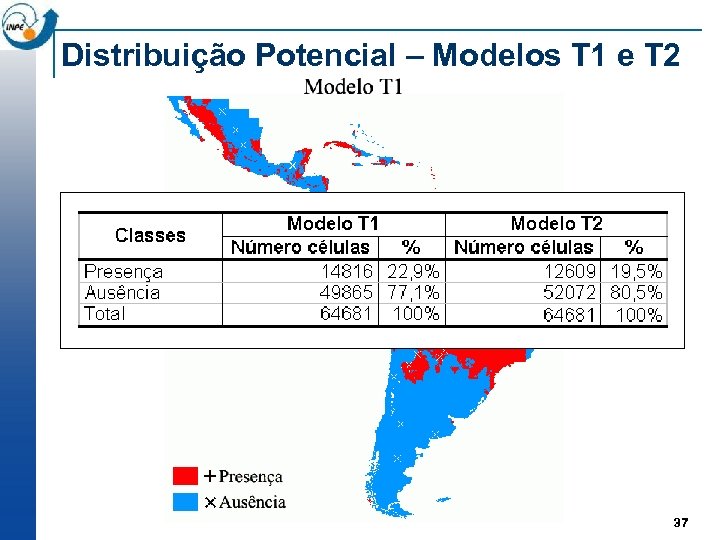
Distribuição Potencial – Modelos T 1 e T 2 37
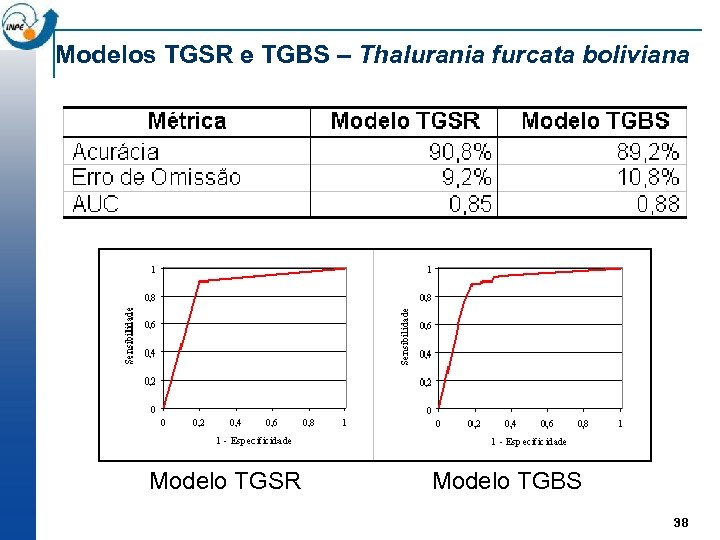
Modelos TGSR e TGBS – Thalurania furcata boliviana Modelo TGSR Modelo TGBS 38
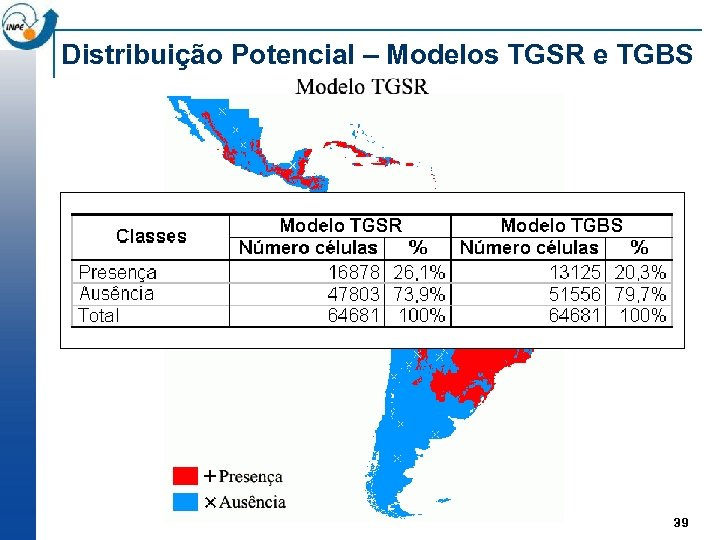
Distribuição Potencial – Modelos TGSR e TGBS 39

Roteiro n Introdução n Referencial Teórico: ¨ Representação do espaço bi-dimensional e vizinhança espacial; ¨ Algoritmos Genéticos; ¨ Model Breeders; ¨ Species Distribution Models. n SAHGA Model Breeder n SAHGA SDM n Conclusões n Referências Bibliográficas 40

Conclusões n Sistemas de análise de dados geoespaciais que utilizam AG negligenciam os efeitos da dependência espacial; n Prova de conceito SAHGA – Spatially Aware Hybrid Genetic Algorithm relacionamentos espaciais GPM; n Algoritmo de uso múltiplo: SAHGA MB Dados sócio-econômicos; ¨ SAHGA SDM Strix varia e Thalurania furcata boliviana. ¨ 41

Conclusões n SAHGA MB: ¨ Ajuste de modelos sem e com relacionamentos espaciais (GPM); ¨ Modelos ajustados são distintos influência dos relacionamentos espaciais. ¨ Ambos estimam adequadamente o valor padronizado da variável dependente. 42
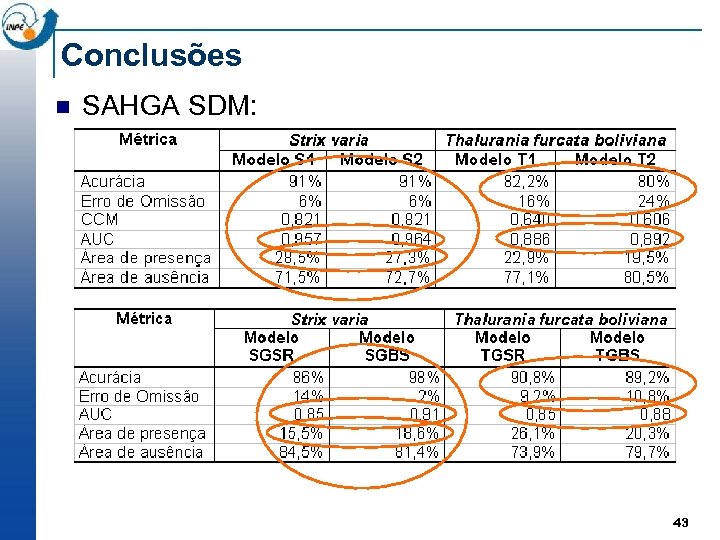
Conclusões n SAHGA SDM: 43

Conclusões n C Representação de conhecimento do especialista: ¨ No espaço relativo SAHGA MB: n n ¨ No espaço absoluto SAHGA SDM: n n n Associações entre estados independem da distância; Válida para alguns estados. Pesos Wij variam em função da distância; 0 – 50 km = 1, 0; 50 – 100 km = 0, 5. C Adaptabilidade do algoritmo modelos mais complexos: Adaptação da estrutura cromossômica; ¨ Reescrita da função de aptidão. ¨ 44

Trabalhos Futuros n Geração automática da GPM: ¨ n Outros tipos de modelos: ¨ n n n Relacionamentos pré-definidos: toca, intercepta, perto de, etc. Estruturas cromossômicas e funções de aptidão prédefinidas; Rotinas de pré-análise de dados; Geração automática de pontos de pseudoausência; GPM dinâmicas: ¨ Análise de dados espaço-temporais. 45

Roteiro n Introdução n Referencial Teórico: ¨ Representação do espaço bi-dimensional e vizinhança espacial; ¨ Algoritmos Genéticos; ¨ Model Breeders; ¨ Species Distribution Models. n SAHGA Model Breeder n SAHGA SDM n Conclusões n Referências Bibliográficas 46

Referências Bibliográficas AGUIAR, A. P. D. et al. Modeling spatial relations by generalized proximity matrices. In: Brazilian Symposium on Geoinformatics, 5, 2003. Campos do Jordão - SP. Anais eletrônicos. . . São José dos Campos: INPE, Nov. 2003. Disponível em: <http: //www. geoinfo/geoinfo 2003/papers/geoinfo 200311. pdf>. Acesso em: 04/07/2006. BRAGA, A. C. S. Curvas ROC: aspectos funcionais e aplicações. 2000. 243 p. Tese (Doutorado em Engenharia de Produção e Sistemas) - Universidade do Minho, Braga. CENTRO DE REFERÊNCIA EM INFORMAÇÃO AMBIENTAL; ESCOLA POLITÉCNICA DA USP; INSTITUTO NACIONAL DE PESQUISAS ESPACIAIS. open. Modeller. 2008. Disponível em: <http: //openmodeller. sourceforge. net/>. Acesso em: 12/07/2008. DE JONG, K. A. An analysis of the behavior of a class of genetic adaptive systems. 1975. 256 p. Tese (Ph. D. in Computer and Communication Sciences) - University of Michigan, Ann Arbor. GREFENSTETTE, J. J. Optimization of control parameters for genetic algorithms. IEEE transactions on systems, man and cybernetics, v. 16, n. 1, p. 122 -128, Jan. /Fev. 1986. GUISAN, A. ; ZIMMERMANN, N. E. Predictive habitat distribution models in ecology. Ecological Modelling, v. 135, n. 2 -3, p. 147 -186, Dez. 2000. HOLLAND, J. H. Adaptation in natural and artificial systems. Cambridge: MIT Press, 1992. 228 p. 47

Referências Bibliográficas KANSAS UNIVERSITY. Desktop. Garp. 2007. Disponível em: <http: //www. nhm. ku. edu/desktopgarp/>. Acesso em: 03/05/2008. KIRKPATRICK, S. ; GELATT, C. D. ; VECCHI, M. P. Optimization by simulated annealing. Science, v. 220, n. 4598, p. 671 -680, Maio 1983. METROPOLIS, N. et al. Equation of state calculations by fast computing machines. The Journal of Chemical Physics, v. 21, n. 6, p. 1087, Jun. 1953. MEYER, E. M. Ecological niche modelling: inter-model variation, best-subset models selection. In: Workshop on Biodiversity Data Modelling, 2005. Cidade do México. Anais eletrônicos. . . Copenhague: GBIF, Abr. 2005. Disponível em: <http: //www. gbif. org/prog/ocb/modeling_workshop/bangalore/presentations/ENMIV>. Acesso em: 21/10/2007. MICHALEWICZ, Z. Genetic algorithms + data structures = evolution programs. 3. ed. Berlin: Springer-Verlag, 1996. 387 p. NIX, H. A. A biogeographic analysis of Australian elapid snakes. In: LONGMORE, R. (Ed. ) Atlas of elapid snakes of Australia. Canberra: Australian government publishing service, v. 7, 1986. p. 4– 15. (Australian flora and fauna series). OPENSHAW, S. ; OPENSHAW, C. Artificial intelligence in geography. West Sussex: John Wiley & Sons, 1997. 348 p. 48

Referências Bibliográficas PEDROSA, B. M. Ambiente computacional para modelagem dinâmica. 2003. 71 p. Tese (Doutorado em Computação Aplicada) - Instituto Nacional de Pesquisas Espaciais, São José dos Campos. SANTA CATARINA, A. ; BACH, S. L. Estudo do efeito dos parâmetros genéticos sobre a solução otimizada e sobre o tempo de convergência em algoritmos genéticos com codificações binária e real. Acta Scientiarum. Technology, v. 25, n. 2, p. 147 -152, Jul. /Dez. 2003. SIQUEIRA, M. F. Uso de modelagem de nicho fundamental na avaliação do padrão de distribuição geográfica de espécies vegetais. 2005. 107 p. Tese (Doutorado em Ciências de Engenharia Ambiental) - Universidade de São Paulo, São Carlos. STOCKWELL, D. R. B. ; PETERS, D. The GARP modeling system: problems and solutions to automated spatial prediction. International Journal of Geographical Information Science, v. 13, n. 2, p. 143 -158, Mar. 1999. 49
9f37497d32654327c8989e1048a5f1a8.ppt