Safety Verification of Model Helicopter Controller Using Hybrid

Safety Verification of Model Helicopter Controller Using Hybrid Input/Output Automata Sayan Mitra MIT Hybrid Systems: Computation and Control Prague, Czech Republic 2003 Joint work with Yong Wang (U. Beijing), Nancy Lynch, Eric Feron HSCC 03 MIT LCS

Verification Techniques • Algorithmic – Model checking e. g. [Alur, et al. 95] • Automatic: Hy. Tech • Essentially for finite-state systems, subclass of linear hybrid systems – Over approximating set of unsafe states [Bayen, et al. 02] • Deductive – Invariant assertions, simulation relations e. g. [Manna, Sipma 98] • Can accommodate infinite-state systems: STe. P • Requires human effort – User interaction HSCC 03 MIT LCS

Talk Outline • Introduction ٭ • • Hybrid I/O Automata definitions Specification of Quanser Safety Verification Conclusions HSCC 03 MIT LCS

The HIOA Model [Lynch, Segala, Vaandrager 01, 03] • General, mathematical modeling framework. – States, discrete transitions – Trajectories: Maps left closed intervals of time to variable values • Support for decomposing hybrid system descriptions: – External behavior: Models interaction of component with environment. – Composition: Synchronizes external actions, external “flows”; respects external behavior. – Levels of abstraction: Implementation notion • Can incorporate analysis methods from: – CS: Invariants, simulation relations, compositional methods. – Control theory: Invariant sets, stability analysis, robust control. HSCC 03 MIT LCS

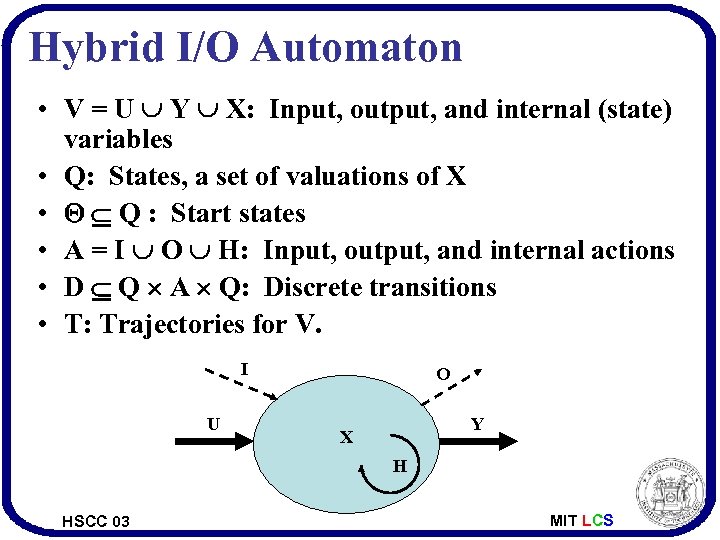
Hybrid I/O Automaton • V = U Y X: Input, output, and internal (state) variables • Q: States, a set of valuations of X • Q : Start states • A = I O H: Input, output, and internal actions • D Q A Q: Discrete transitions • T: Trajectories for V. I U O Y X H HSCC 03 MIT LCS

Trajectory Axioms and Executions • Set T of trajectories is closed under: – Prefix – Suffix – Countable concatenation • fstate, lstate • Execution fragment: 0 a 1 1 a 2 2 …, where: • Each i is a trajectory of the automaton and • Each ( i. lstate, ai , i+1. fstate) is a discrete step. • Execution: – Execution fragment beginning in a start state. HSCC 03 MIT LCS

Model Helicopter System • Manufactured by Quanser • User controllers not necessarily safe, can crash the helicopter on the table. • Supervisory pitch controller needed to ensure safety. – Safe operating region – Saturated actuator outputs : Umin or Umax • Must contend with – Sensor errors – Actuator delay HSCC 03 MIT LCS

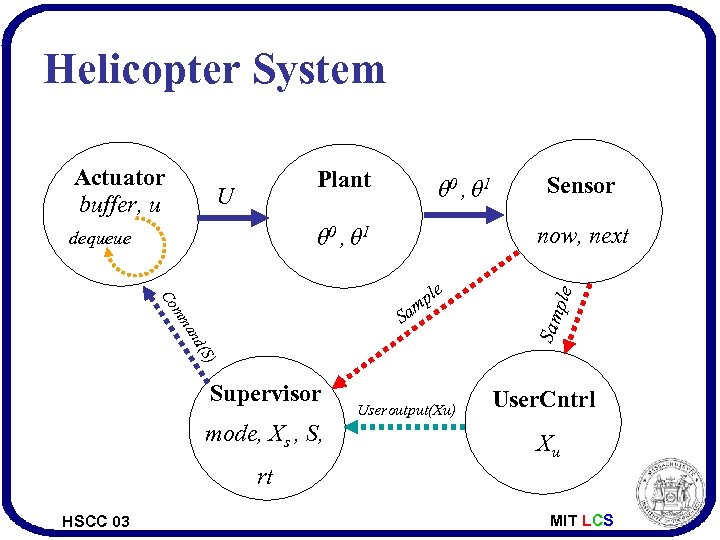
Helicopter System Plant θ 0 , θ 1 now, next θ 0 , θ 1 dequeue Sensor m m mm C C Co ple m Sa ple U d(S d(S an an an Sam Actuator buffer, u ) ) ) Supervisor mode, Xs , S, Useroutput(Xu) User. Cntrl Xu rt HSCC 03 MIT LCS

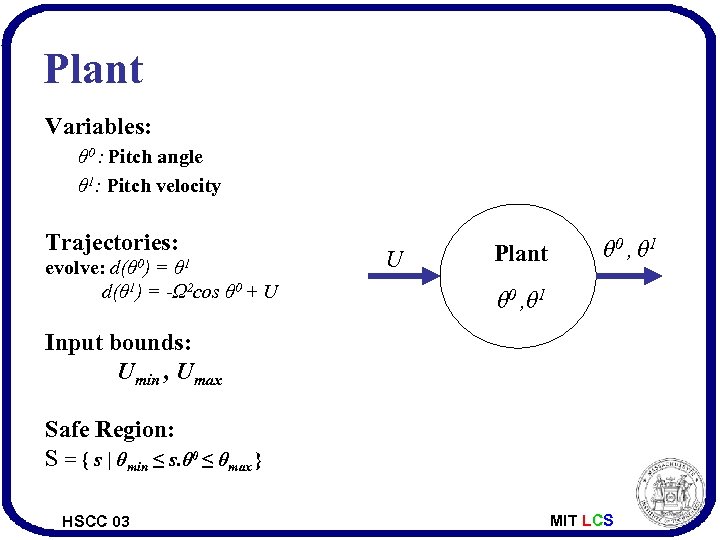
Plant Variables: θ 0 : Pitch angle θ 1: Pitch velocity Trajectories: evolve: d(θ 0) = θ 1 d(θ 1) = -Ω 2 cos θ 0 + U U Plant θ 0 , θ 1 Input bounds: Umin , Umax Safe Region: S = { s | θmin ≤ s. θ 0 ≤ θmax } HSCC 03 MIT LCS

Sensor Discrete transition: Sample(θ 0 d , θ 1 d θ 0 , θ 1 ) } Trajectories: evolve: d(now) = 1 stopping condition: now = next HSCC 03 Nondeterministic choice now, next Sample(θ 0 d , θ 1 d ) precondition: now = next and θ 0 d є [θ 0 - є 0 , θ 0+ є 0 ] and θ 1 d є [θ 1 - є 1, θ 1 - є 1] effect: next = next + Δ Sensor MIT LCS

User Controller • Arbitrarily bad user • On receiving Sample, – Useroutput(Xu) – Non deterministic choice, Xu є [Umin, Umax ] HSCC 03 MIT LCS

Actuator • Actuator delay Ta – modeled as a FIFO queue of Supervisor(User) outputs – buffer: length [Ta / Δ] • Enqueue S received from supervisor • Dequeue u from buffer head, – u changes discretely – Made into piece-wise continuous output U HSCC 03 MIT LCS

Modeling Actuator Delay • Ta Currently modeled as a single discrete jump from Umin to Umax after time Ta. • Alternatively – Approximate exponential rise by adding k intermediate values in the buffer, for every command from the supervisor. • Output from buffer will change every Δ/k time. Ta – Model as continuous function HSCC 03 MIT LCS

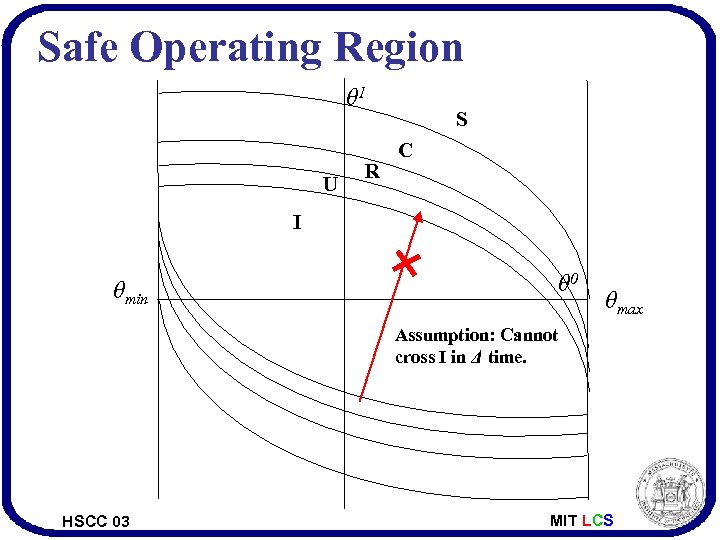
Safe Operating Region θ 1 U R S C I θmin θ 0 θmax Assumption: Cannot cross I in Δ time. HSCC 03 MIT LCS

Supervisor Command(S) Sample mode, Xs , S, Userout(Xu) rt • On receiving sample, computes Xs • If s is above I+ then Xs = Umin • If s is below I then Xs = Umax • On receiving useroutput(Xu), computes S – If mode = user then • If s is in U then S = Xu • Else mode = supervisor ; S = Xs – If mode = supervisor then • If s is in I then S = Xu ; mode = user • Else S = Xs HSCC 03 MIT LCS

Safety Verification • Assertional Proofs – Reasoning based on current state of the system • Finding the invariants is challenging – Strengthen statement • Proofs are easy, for proving I – Base case: I – Discrete part: s a s’ є D, show I(s) implies I(s’) – Continuous part: closed τ є T, show I(fstate(τ)) implies I(lstate(τ)) HSCC 03 MIT LCS

Key Lemmas • All trajectories are closed • Any trajectory τ є T, ltime(τ) - ftime(τ) ≤ Δ. HSCC 03 MIT LCS

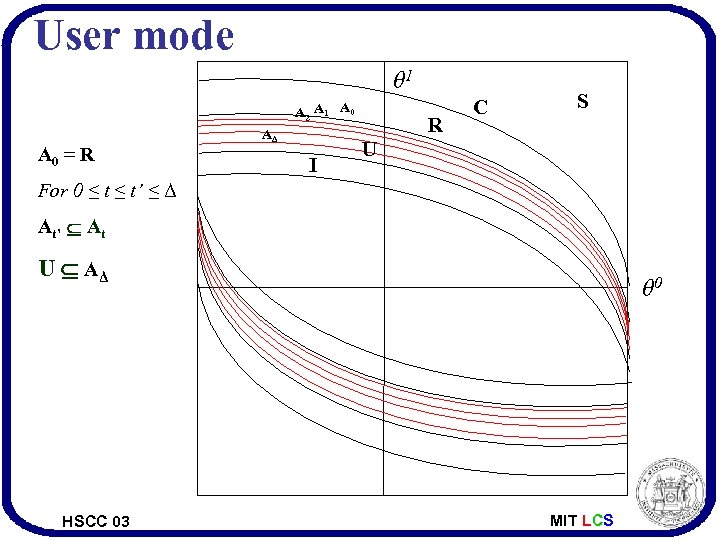
User mode θ 1 A 2 A 1 A 0 = R AΔ I R C S U For 0 ≤ t’ ≤ Δ At’ At U AΔ HSCC 03 θ 0 MIT LCS

User mode Safety • Any reachable state in the user mode is within R. • Proof: – Discrete part is easy – Any closed trajectory τ є T, if fstate(τ) є At then lstate(τ) є At-ltime(τ). HSCC 03 MIT LCS

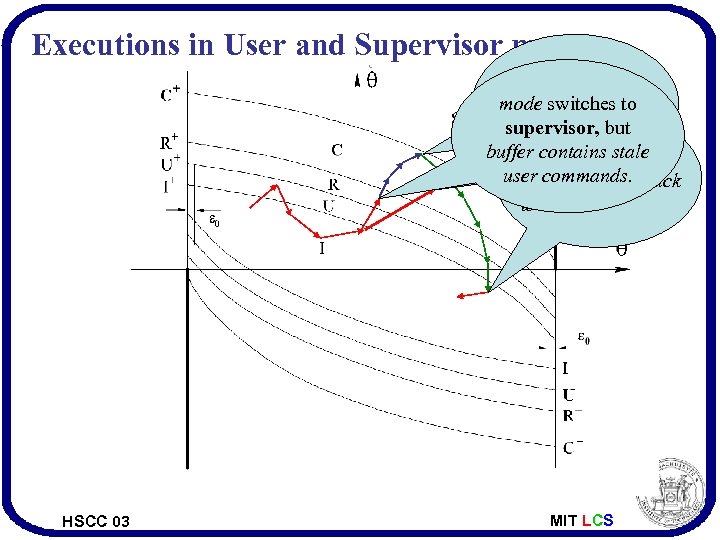
Executions in User and Supervisor modes buffer flushed, mode switches to Supervisor mode Cannot go outside R supervisor, but kicks in. from U, in the user buffer contains I and Returns to stale mode user commands. back mode switches to user. HSCC 03 MIT LCS

Supervisor mode Correct input to plant • If s is above I+ then last [rt/Δ] entries in buffer are Umin – rt: stopwatch for supervisor mode • Similarly, s is below I- then … Umax Settling phase rt ≤ Ta • Any reachable state is within C – All trajectories starting from within R remains within C – Proof similar to User mode Recovery phase rt > Ta • Any reachable state is within C – Proof: At any point on boundary of C, the vector field points inwards HSCC 03 MIT LCS

Conclusions • Design of supervisory controller – Controller has been implemented [Ishutkina]. • Specification Language • Demonstration of HIOA framework – Specification • Compositional • Nondeterminism models uncertainties in devices or user inputs. – Purely assertional proofs • Discrete and continuous parts • CS and Control Theory techniques • Current/Future Work – Performance guarantees for mobile computing algorithms – Theorem prover support HSCC 03 MIT LCS

Thank You. Questions ? HSCC 03 MIT LCS

HSCC 03 MIT LCS

Current/Future Work • Incorporate control theory methods: – Invariant sets, Stability analysis using Lyapunov functions, robust control methods. • More examples: – Systems with more complicated discrete behavior and dynamics, e. g. mobile computing, embedded systems. • Develop analysis tools for HIOA programs: – Theorem-provers, automated tools – As extension to IOA toolset HSCC 03 MIT LCS