сад дом огород Методика формирования у младших школьников

сад дом огород Методика формирования у младших школьников представлений о площади и ее измерении. Ознакомление с единицами площади и их соотношением.

Единицы площади За основную единицу площади в метрической системе мер принят Метр² Более крупные (кратные) Более мелкие (дольные) 1 кв. декаметр (ар) = 100 м² 1 кв. дециметр (дм) = 0, 01 м² 1 кв. гектометр = 10000 м² 1 кв. сантиметр (см) = 0, 0001 м² 1 кв. километр (км) = 1 000 м² 1 кв. миллиметр (мм) = 0, 000001 м² 1 дкм², 1 гм², 1 км² 1 дм², 1 см², 1 мм² 1 а 1 га 1 км² = 100 га 1 га= 100 а 1 а= 100 м²

Площадь как величина выражает общее свойство плоских предметов. Ц е л ь и з у ч е н и я - сформировать у учащихся общее представление о площади и выработать умение вычислять площадь прямоугольника.

1. Введение понятия «площадь фигуры» (М-3, ч. 1, с. 50). Понятие «площадь» вводится с опорой на представления детей о том, что каждая фигура занимает определенное место на плоскости. Учитель показывает две фигуры, одна из которых целиком помещается внутри другой, и сообщает, что в этом случае в математике принято говорить, что площадь одной фигуры больше (меньше) площади другой. - Какая фигура занимает меньше места на плоскости? (треугольник) Значит, площадь треугольника меньше площади круга. - Вы определили это на глаз. Как можно проверить? (наложить треугольник на круг) - Верно. Показываю. - Какая фигура занимает больше места на плоскости? (круг) Значит, площадь круга больше площади треугольника.

2. Сравнение площадей: а) по внешнему виду (на глаз); б) наложением; в) путем подсчета числа единичных квадратов. Для способов а) и б) используются модели и рисунки в учебнике. Можно предложить сравнить следующие фигуры: 1 2 3 4 5 Путем наложения их друг на друга учащиеся устанавливают, что площади 1 и 2 фигур одинаковы, а площадь 4 меньше площади 5, т. к. вся 4 фигура помещается внутри 5 и т. д.

Для введения способа в) учитель создает проблемную ситуацию – показывает фигуры, площади которых нельзя сравнить наложением. С обратной стороны эти фигуры разбиты на одинаковые квадраты. Учитель переворачивает фигуры обратной стороной и дети догадываются, что надо пересчитать число квадратов в каждой фигуре. Фигура, которая содержит больше таких квадратов, имеет большую площадь.

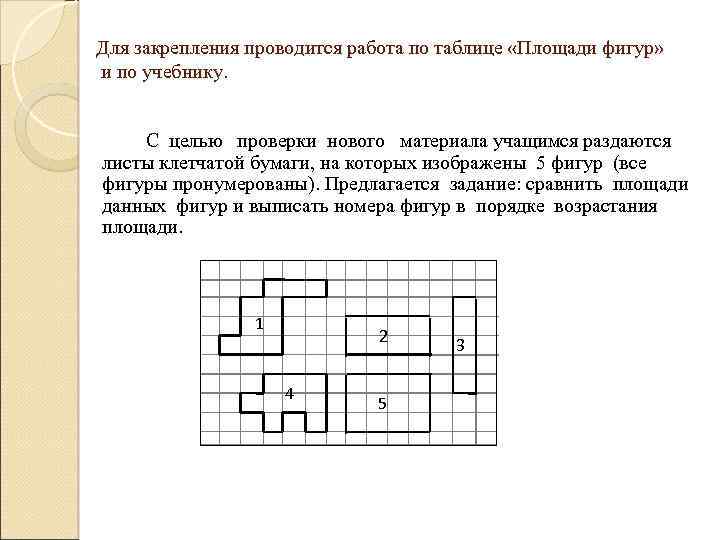Для закрепления проводится работа по таблице «Площади фигур» и по учебнику. С целью проверки нового материала учащимся раздаются листы клетчатой бумаги, на которых изображены 5 фигур (все фигуры пронумерованы). Предлагается задание: сравнить площади данных фигур и выписать номера фигур в порядке возрастания площади. 1 2 4 5 3

3. Знакомство с единицей площади – квадратным сантиметром Учителю необходимо помнить: Единицы площади вводятся в натуральную величину. Знакомство с первой единицей площади можно провести по следующему плану: 1. Создание проблемной ситуации с целью введения единой единицы площади. 2. Обозначение и чтение. 3. Отражение в тетради. 4. Изготовление фигур из квадратных сантиметров.

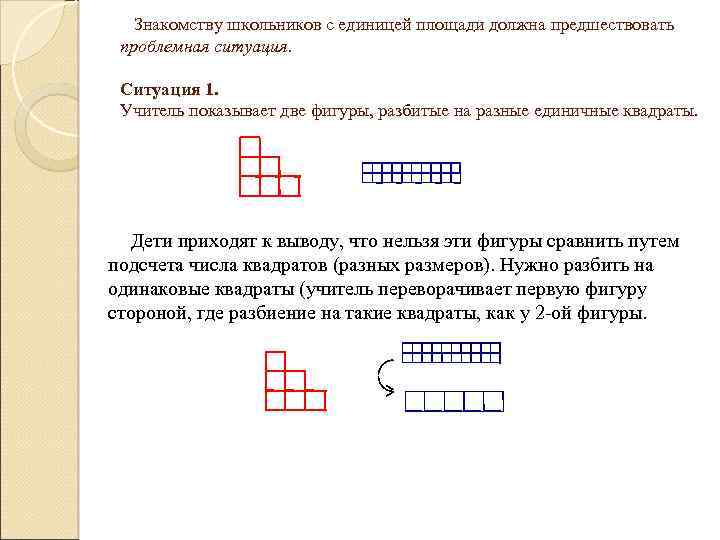Знакомству школьников с единицей площади должна предшествовать проблемная ситуация. Ситуация 1. Учитель показывает две фигуры, разбитые на разные единичные квадраты. Дети приходят к выводу, что нельзя эти фигуры сравнить путем подсчета числа квадратов (разных размеров). Нужно разбить на одинаковые квадраты (учитель переворачивает первую фигуру стороной, где разбиение на такие квадраты, как у 2 -ой фигуры.

Ситуация 2. - Чему равна площадь каждого прямоугольника? - Площадь первого прямоугольника 8 кв. ед. , а второго 32 кв. ед. - Наложим один прямоугольник на другой. Что видим? (они совпали) - Значит, что можно сказать о площади этих прямоугольников? (Они равны. ) - Чему была равна площадь каждого прямоугольника? - Как могло так получиться? Какой вывод можем сделать? - Верно, нужно ввести единую единицу площади, это квадратный сантиметр. Квадратный сантиметр - это площадь квадрата со стороной 1 см. Показываю: 1 см 2

З а д а н и е. Найдите в учебном пособии Н. Б. Истоминой «Методика обучения математике в начальных классах» (с. 95 100) другие проблемные ситуации, которые можно использовать на уроке с целью введения первой 2 единицы площади - см.

4. Измерение площади с помощью см 2 Для того чтобы учащиеся освоили процесс измерения площади, полезно раздать им геометрические фигуры и предложить измерить их площади, пользуясь моделью квадратного сантиметра. Это задание особенно важно, так как в процессе его выполнения учащиеся осознают, что измерить площадь фигуры - значит узнать, сколько квадратных сантиметров она содержит. При этом используют различные способы:

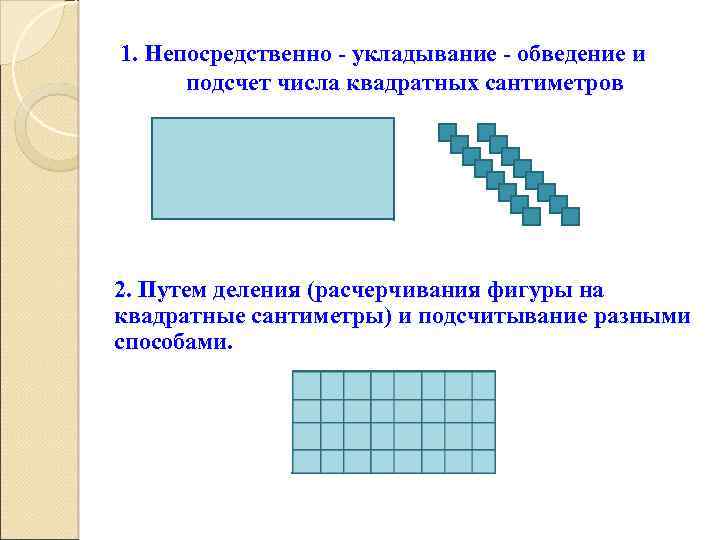1. Непосредственно - укладывание - обведение и подсчет числа квадратных сантиметров 2. Путем деления (расчерчивания фигуры на квадратные сантиметры) и подсчитывание разными способами.

3. Путем наложения готовой сетки квадратных сантиметров - палетки. Учитель сообщает, что удобнее не расчерчивать каждый раз фигуру, а использовать готовую сеть из квадратных сантиметров на прозрачной бумаге. Такую сеть называют п а л е т к о й.

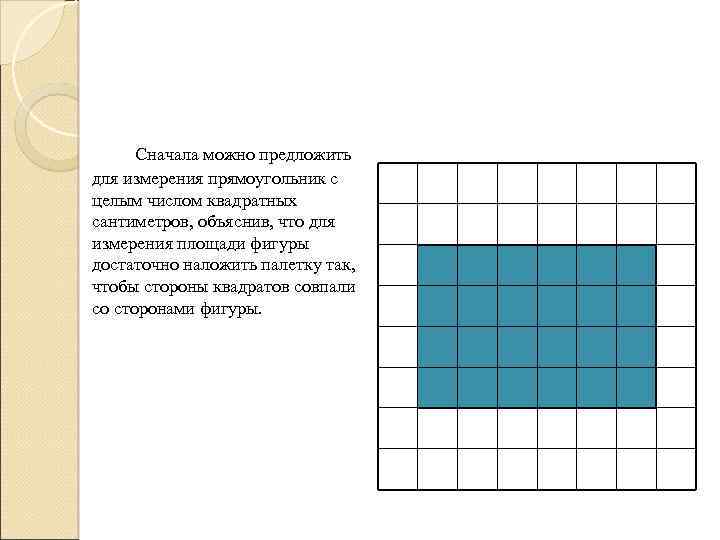Сначала можно предложить для измерения прямоугольник с целым числом квадратных сантиметров, объяснив, что для измерения площади фигуры достаточно наложить палетку так, чтобы стороны квадратов совпали со сторонами фигуры.

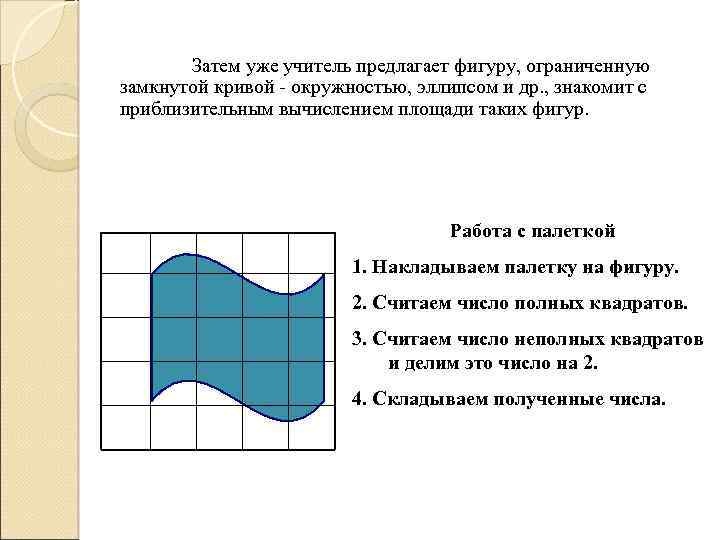Затем уже учитель предлагает фигуру, ограниченную замкнутой кривой - окружностью, эллипсом и др. , знакомит с приблизительным вычислением площади таких фигур. Работа с палеткой 1. Накладываем палетку на фигуру. 2. Считаем число полных квадратов. 3. Считаем число неполных квадратов и делим это число на 2. 4. Складываем полученные числа.

З а д а н и е. Найдите в учебниках М-3 и М-4 страницы, связанные с изучением понятия «площадь» . Приведите упражнения, которые предлагаются ученикам с целью формирования у них представлений: а) о площади; б) об ее измерении; в) о единице площади – квадратном сантиметре и об измерении площадей фигур с помощью этой модели. Составьте упражнения, которые вы могли бы предложить им с этой же целью.

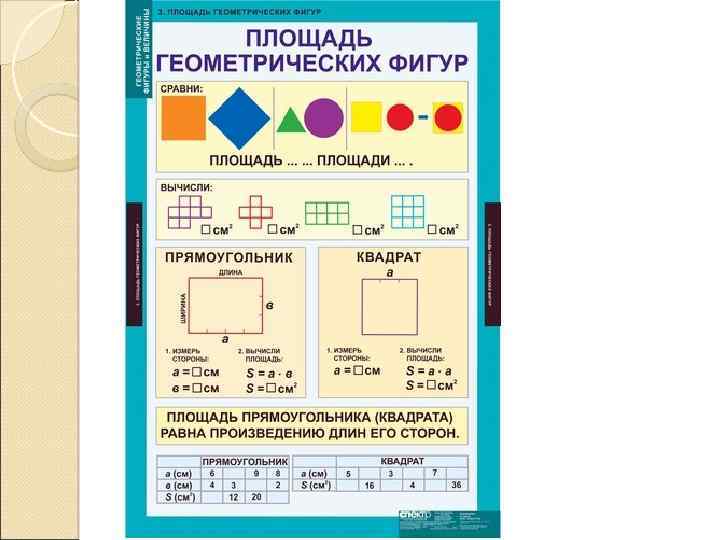
5. Вычисление площади прямоугольника. Опираясь на представления о площади и ее измерении и используя единицу площади – квадратный сантиметр, учащиеся знакомятся с правилом нахождения площади прямоугольника. Это правило иллюстрируется на конкретных примерах. Сначала рассматривают прямоугольники, которые уже разделены на квадратные сантиметры. Их площадь находят путем подсчета квадратных сантиметров в одном ряду, а затем полученное число умножают на число рядов. В одном ряду 6 см 2 , таких рядов 4: 6 4 = 24 (см 2 ) Очень важно при этом установить соответствие между длиной прямоугольника и числом квадратных сантиметров, прилегающих к длине; шириной прямоугольника и числом рядов.

Затем дети чертят прямоугольник по заданным длинам сторон, разбивают его на ряды, а один ряд на квадраты и снова убеждаются в соответствии: если длина 4 2 см, то в одном ряду, прилегающем к этой стороне, содержится 4 см , если ширина 3 см, то таких рядов оказывается 3. Делается вывод: Чтобы вычислить площадь прямоугольника, узнают его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел. Далее включаются устные и письменные задания на вычисление площади прямоугольников (квадратов) и периметров этих фигур.

6. Знакомство с квадратным дециметром. При введении новой единицы площади - квадратного дециметра можно поступить следующим образом: 1. Нарисовать на доске прямоугольник и предложить уч-ся измерить его 2 площадь, пользуясь двумя моделями – см 2 и дм. Учащиеся убеждаются практически, что использование квадратного сантиметра для измерения площади данной фигуры нерационально. Гораздо удобнее пользоваться большей меркой. 2. Учитель вводит название новой мерки и с помощью наводящих вопросов добивается от детей определения квадратного дециметра, показывает краткую запись – Квадратный дециметр – 1 дм 2

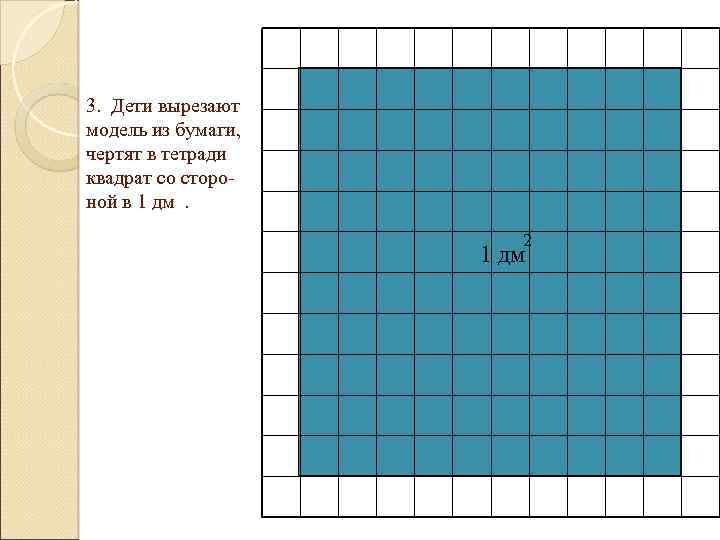3. Дети вырезают модель из бумаги, чертят в тетради квадрат со стороной в 1 дм. 2 1 дм

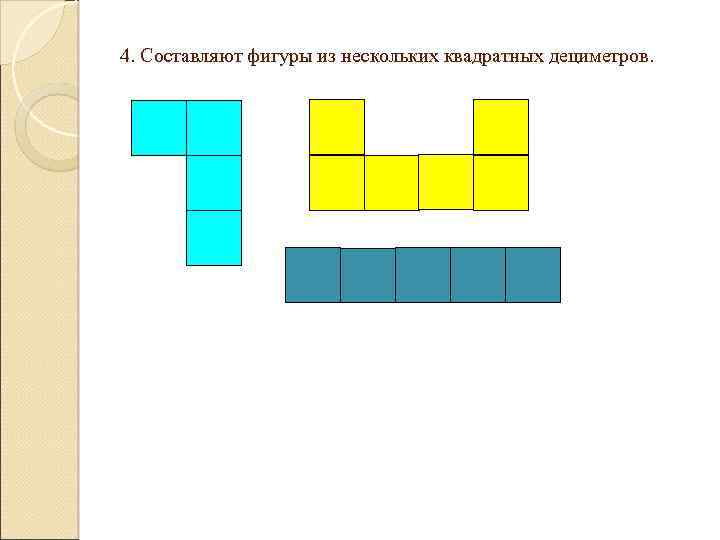4. Составляют фигуры из нескольких квадратных дециметров.

5. Устанавливают соотношение между квадратным дециметром и квадратным сантиметром: 1 дм 2 = 100 см 2

6. Дети учатся заменять мелкие единицы крупными и наоборот. 7. Решаются задачи на вычисление площади в квадратных дециметрах, в квадратных дециметрах и квадратных сантиметрах.

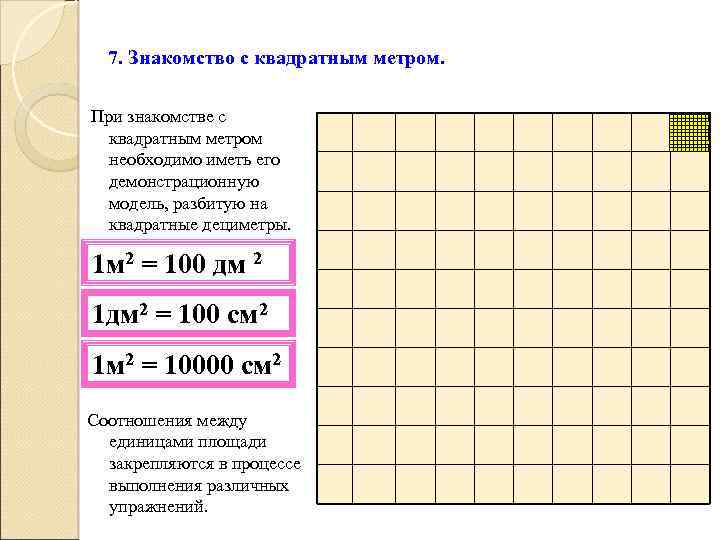7. Знакомство с квадратным метром. При знакомстве с квадратным метром необходимо иметь его демонстрационную модель, разбитую на квадратные дециметры. 1 м 2 = 100 дм 2 1 дм 2 = 100 см 2 1 м 2 = 10000 см 2 Соотношения между единицами площади закрепляются в процессе выполнения различных упражнений.

8. Закрепление знаний путем решения задач на вычисление площади фигур. I. Задачи с пропорциональными величинами (длина, ширина, площадь). В основном - на 4 -е пропорциональное с прямой и обратной зависимостью, решаемые и способом кратного отношения. К их решению нужна подготовительная работа - наблюдение за изменением площади с изменением одной из сторон. Например, № 895, № 896, № 902, № 947. II. Задачи на дроби - двух видов: дробь от числа и числа по доле: № 921, стр. 174; № 959, стр. 180; стр. 200, № 35 - особая задача. III. Задачи, связанные с площадью и периметром прямоугольника (квадрата): № 439, с. 77; № 457.

Очень полезны упражнения в вычислении площади и периметра фигур, составленных из нескольких прямоугольников (с. 197, № 21). В процессе решения задач на вычисление площади и периметра прямоугольников следует показать, что фигуры, имеющие одинаковую площадь, могут иметь неодинаковые периметры, и что фигуры, имеющие одинаковые периметры, могут иметь неодинаковые площади (стр. 197, № 19).

З а д а н и е. Найдите в учебниках М-3 и М-4 страницы, на которых дети знакомятся с единицами площади: 1 дм 2 и 1 м 2. Какие различия существуют в этих учебниках при изучении единиц площади? Приведите конкретные упражнения на закрепление соотношений между единицами площади и возможные рассуждения младших школьников при их выполнении.