
S. Y. Hsu (許世英 ) and K. M. Liu(劉凱銘 ) Department of Electrophysics, National Chiao Tung University Hsinchu , Taiwan NSC 95 -2112 -M-009 -040 and NSC 94 -2120 -M-009 -002 May 29, 2007
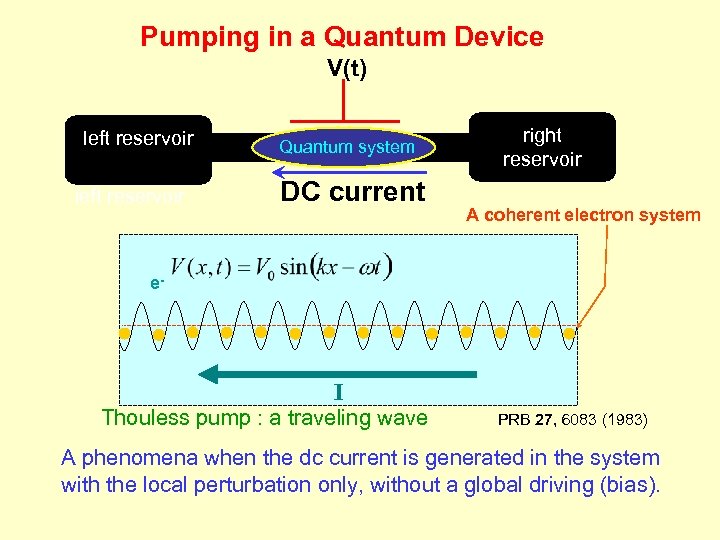
Pumping in a Quantum Device V(t) left reservoir Quantum system I DC current right reservoir A coherent electron system e- I Thouless pump : a traveling wave PRB 27, 6083 (1983) A phenomena when the dc current is generated in the system with the local perturbation only, without a global driving (bias).

l Introduction 2 DEG Ø Gate-confined nanostructures Ø Historical review on charge pumping Ø l Experimental results and discussion Ø l Pumping and Rectification in our QD Summary
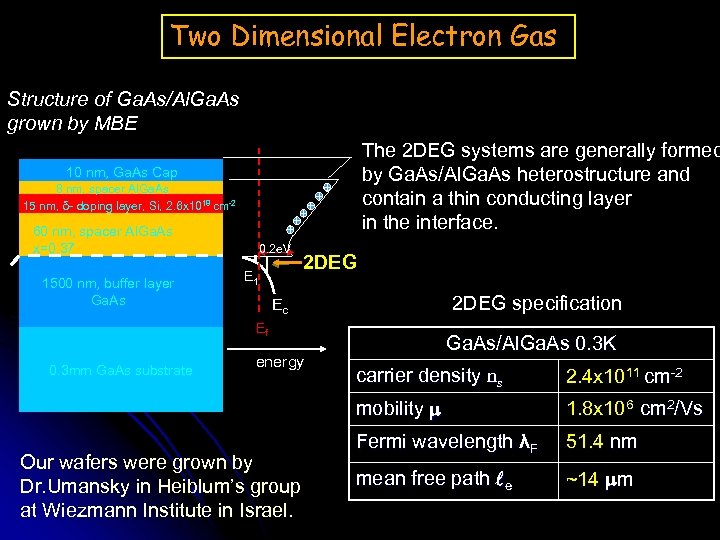
Two Dimensional Electron Gas Structure of Ga. As/Al. Ga. As grown by MBE The 2 DEG systems are generally formed by Ga. As/Al. Ga. As heterostructure and contain a thin conducting layer in the interface. 10 nm, Ga. As Cap 8 nm, spacer Al. Ga. As 15 nm, δ- doping layer, Si, 2. 6 x 1018 cm-2 60 nm, spacer Al. Ga. As x=0. 37 1500 nm, buffer layer Ga. As 0. 2 e. V E 1 2 DEG specification Ec Ef 0. 3 mm Ga. As substrate energy Ga. As/Al. Ga. As 0. 3 K 2. 4 x 1011 cm-2 mobility Our wafers were grown by Dr. Umansky in Heiblum’s group at Wiezmann Institute in Israel. carrier density ns 1. 8 x 106 cm 2/Vs Fermi wavelength λF 51. 4 nm mean free path e ~14 m
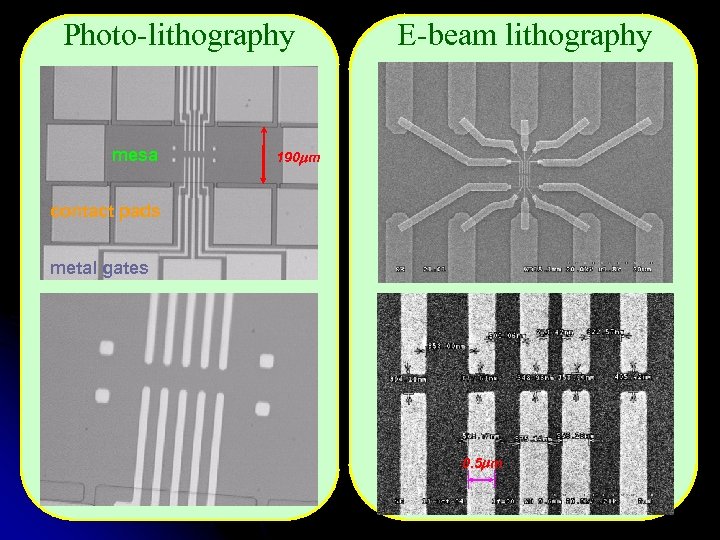
Photo-lithography mesa E-beam lithography 190 m contact pads metal gates 0. 5 m
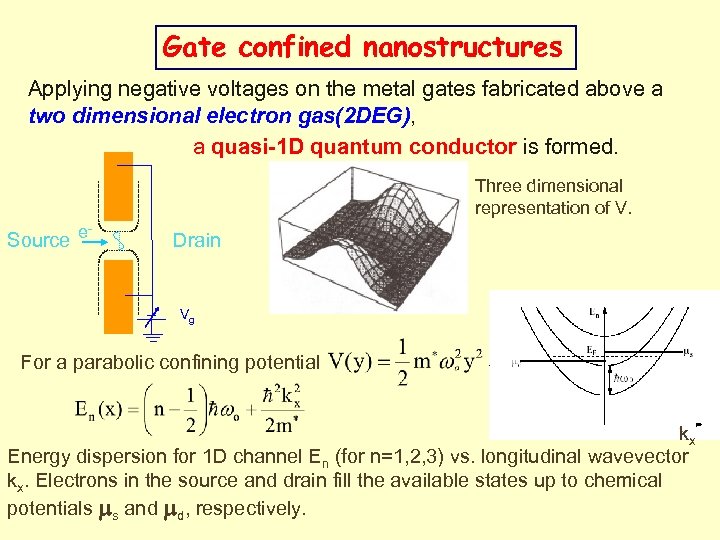
Gate confined nanostructures Applying negative voltages on the metal gates fabricated above a two dimensional electron gas(2 DEG), a quasi-1 D quantum conductor is formed. Three dimensional representation of V. Source e Drain Vg For a parabolic confining potential kx Energy dispersion for 1 D channel En (for n=1, 2, 3) vs. longitudinal wavevector kx. Electrons in the source and drain fill the available states up to chemical potentials s and d, respectively.
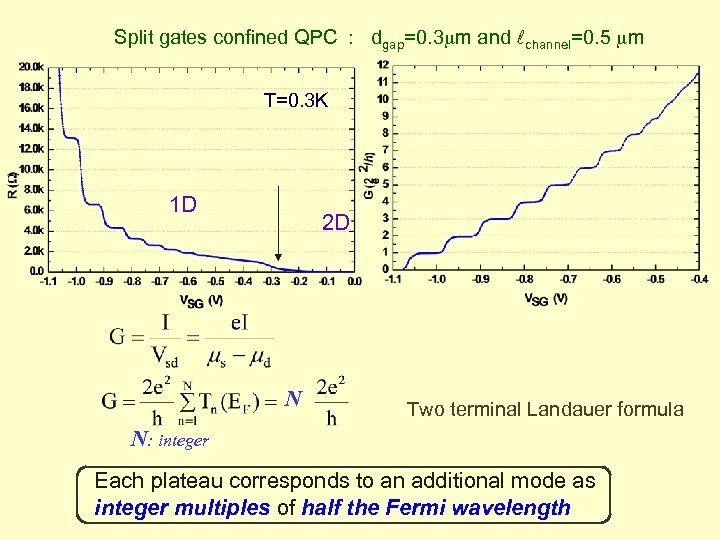
Split gates confined QPC : dgap=0. 3 m and channel=0. 5 m T=0. 3 K 1 D 2 D N Two terminal Landauer formula N: integer Each plateau corresponds to an additional mode as integer multiples of half the Fermi wavelength
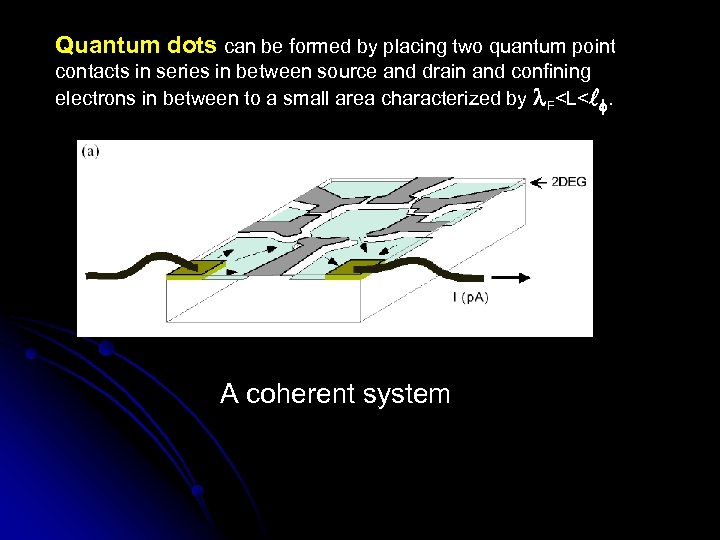
Quantum dots can be formed by placing two quantum point contacts in series in between source and drain and confining electrons in between to a small area characterized by F<L< . A coherent system
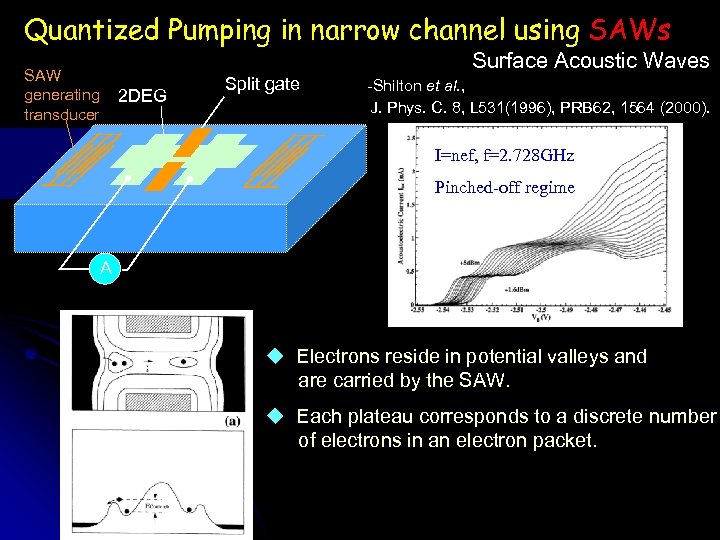
Quantized Pumping in narrow channel using SAWs Surface Acoustic Waves SAW generating transducer 2 DEG Split gate -Shilton et al. , J. Phys. C. 8, L 531(1996), PRB 62, 1564 (2000). I=nef, f=2. 728 GHz Pinched-off regime A u Electrons reside in potential valleys and are carried by the SAW. u Each plateau corresponds to a discrete number of electrons in an electron packet.

Adiabatic Charge Pumping in a QD Brouwer (1998) Vac, 1 sin( t) For an open confined cavity with two parameters modifying wavefunction with a phase shift , use S-matrix and treat the ac field as a weak perturbation The charge Q(m) entering or leaving the cavity through contact m(m=1, 2) in an infinitesimal time: After Fourier Transform, integrating over one period and change of variables PRB 58, 10135 (1998). Vac, 2 sin( t+ ) emissivity
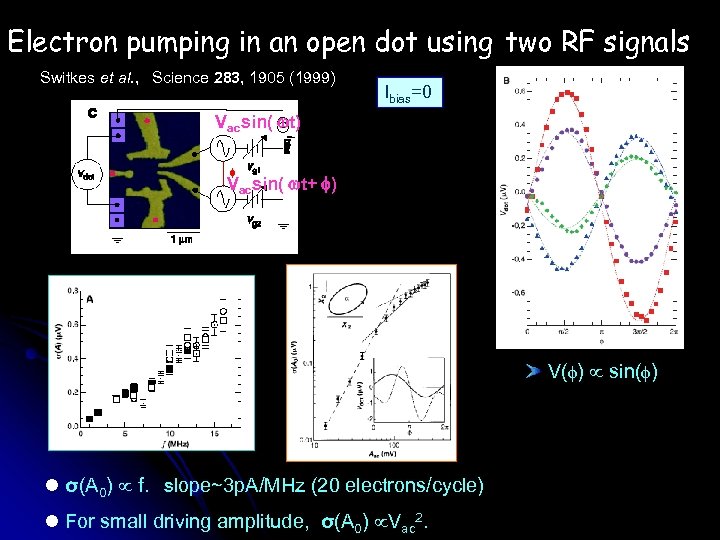
Electron pumping in an open dot using two RF signals Switkes et al. , Science 283, 1905 (1999) Ibias=0 Vacsin( t) Vacsin( t+ ) V( ) sin( ) l σ(A 0) f. slope~3 p. A/MHz (20 electrons/cycle) l For small driving amplitude, σ(A 0) Vac 2.

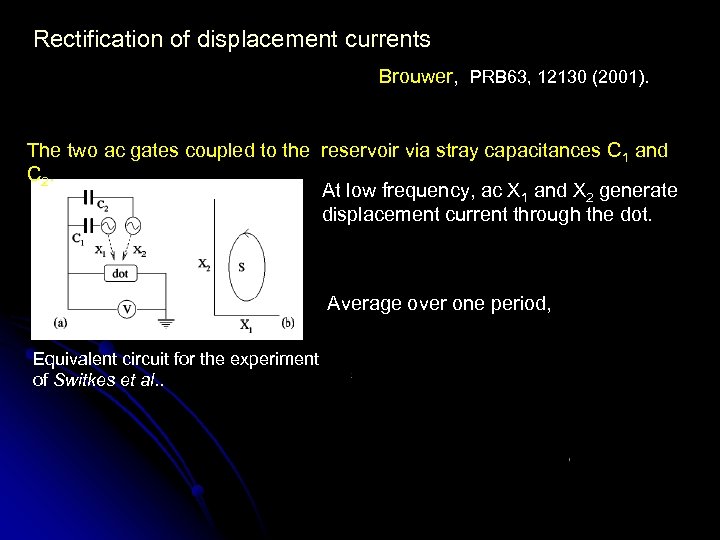
Rectification of displacement currents Brouwer, PRB 63, 12130 (2001). The two ac gates coupled to the reservoir via stray capacitances C 1 and C 2. At low frequency, ac X 1 and X 2 generate displacement current through the dot. Average over one period, Equivalent circuit for the experiment of Switkes et al. .
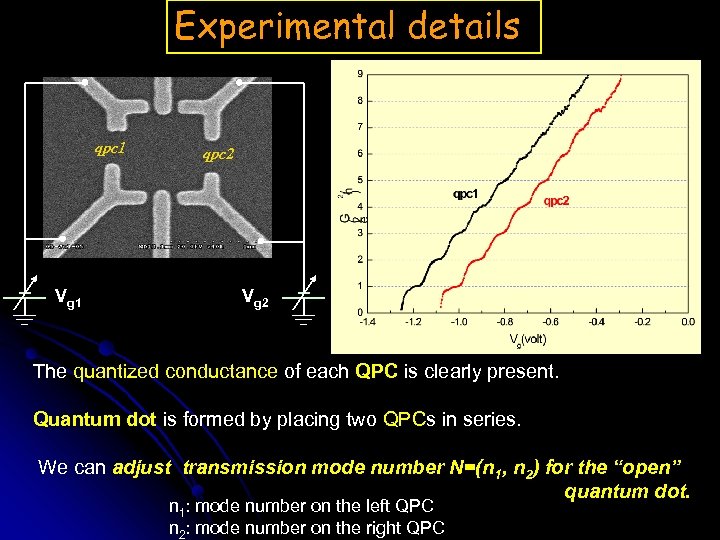
Experimental details qpc 1 Vg 1 qpc 2 Vg 2 The quantized conductance of each QPC is clearly present. Quantum dot is formed by placing two QPCs in series. We can adjust transmission mode number N=(n 1, n 2) for the “open” quantum dot. n 1: mode number on the left QPC n 2: mode number on the right QPC
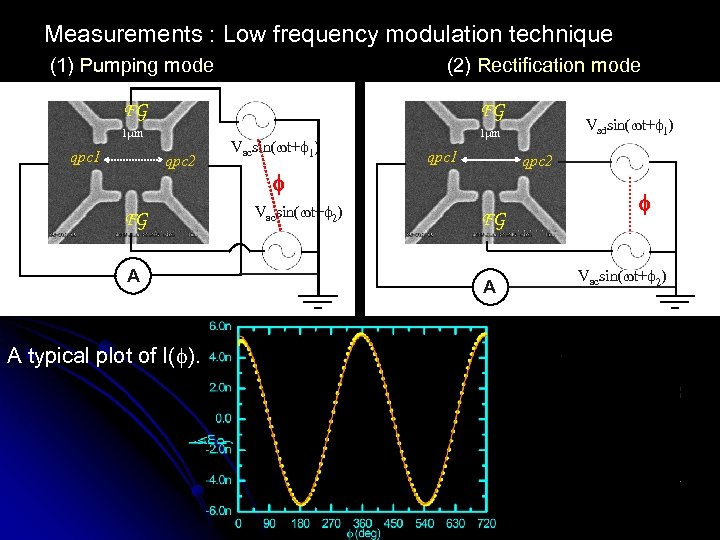
Measurements : Low frequency modulation technique (1) Pumping mode (2) Rectification mode FG FG 1 m qpc 1 qpc 2 FG A A typical plot of I( ). Vacsin( t+ 1) qpc 1 qpc 2 Vacsin( t+ 2) Vsdsin( t+ 1) FG A Vacsin( t+ 2)
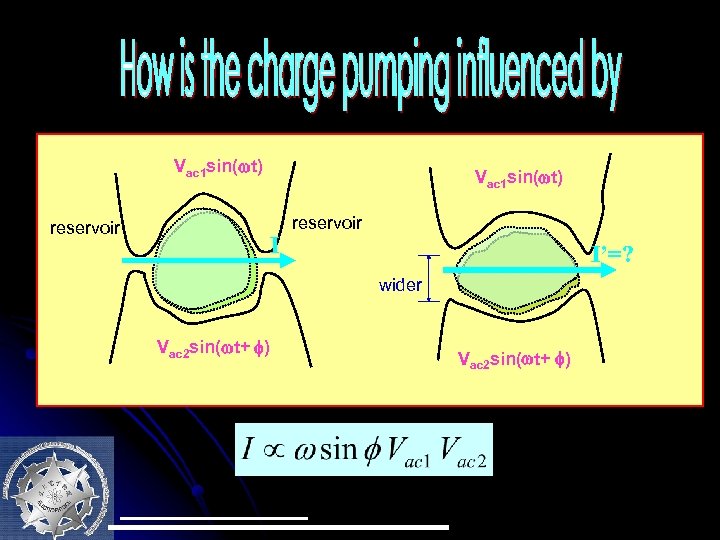
Vac 1 sin( t) reservoir Vac 1 sin( t) I reservoir I’=? wider Vac 2 sin( t+ )

Experimental results DC current amplitude Ip & Irect vs. ac driving amplitude Vac DC current amplitude Ip & Irect vs. ac driving frequency f for different couplings between dot and its reservoir. (n 1, n 2).
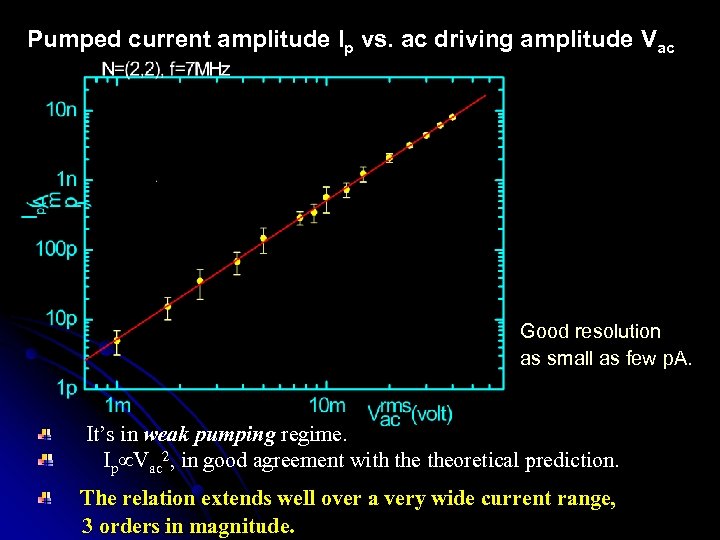
Pumped current amplitude Ip vs. ac driving amplitude Vac Good resolution as small as few p. A. It’s in weak pumping regime. Ip Vac 2, in good agreement with theoretical prediction. The relation extends well over a very wide current range, 3 orders in magnitude.
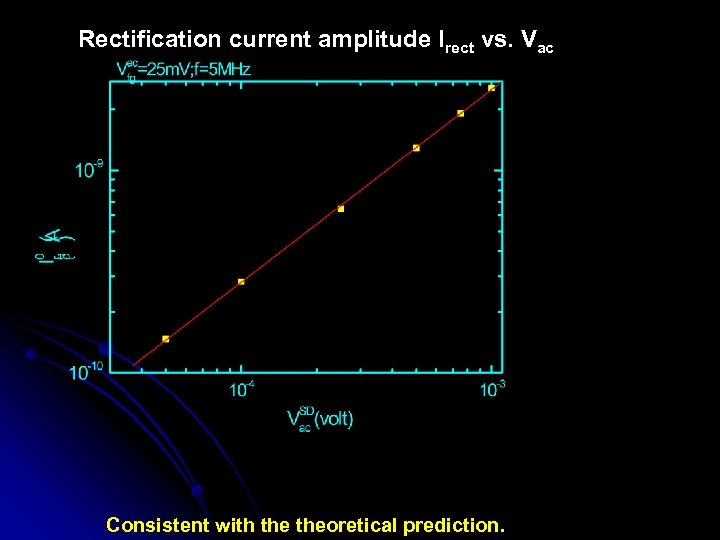
Rectification current amplitude Irect vs. Vac Consistent with theoretical prediction.
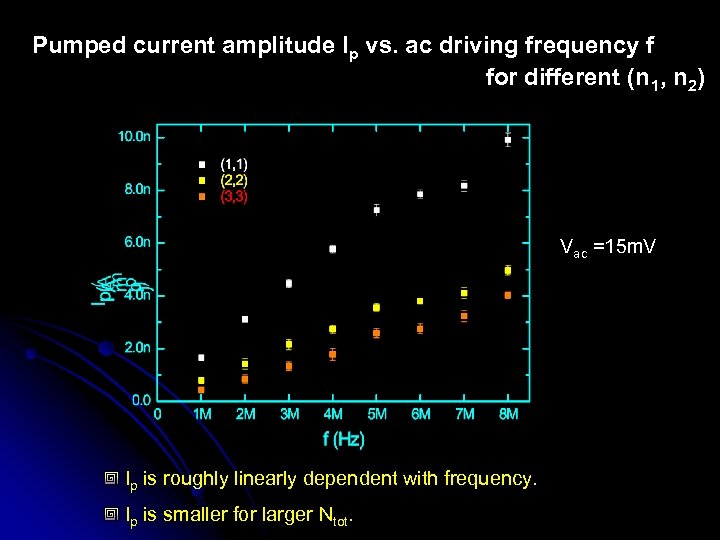
Pumped current amplitude Ip vs. ac driving frequency f for different (n 1, n 2) Vac =15 m. V Ip is roughly linearly dependent with frequency. Ip is smaller for larger Ntot.
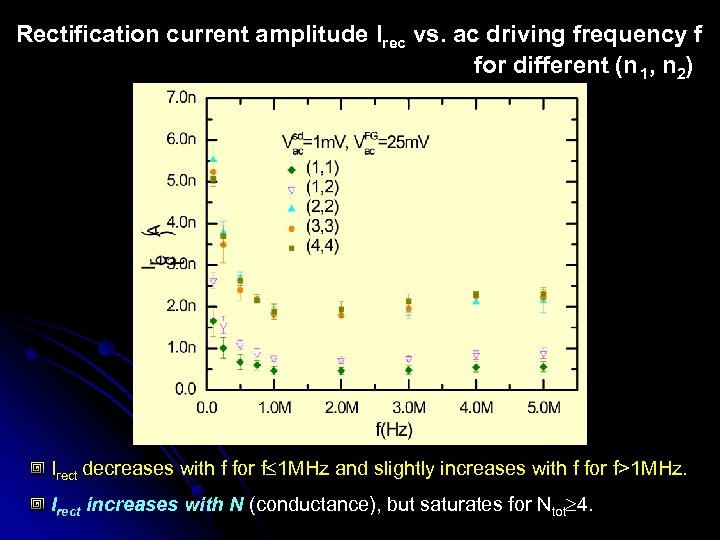
Rectification current amplitude Irec vs. ac driving frequency f for different (n 1, n 2) Irect decreases with f for f 1 MHz and slightly increases with f for f>1 MHz. Irect increases with N (conductance), but saturates for Ntot 4.
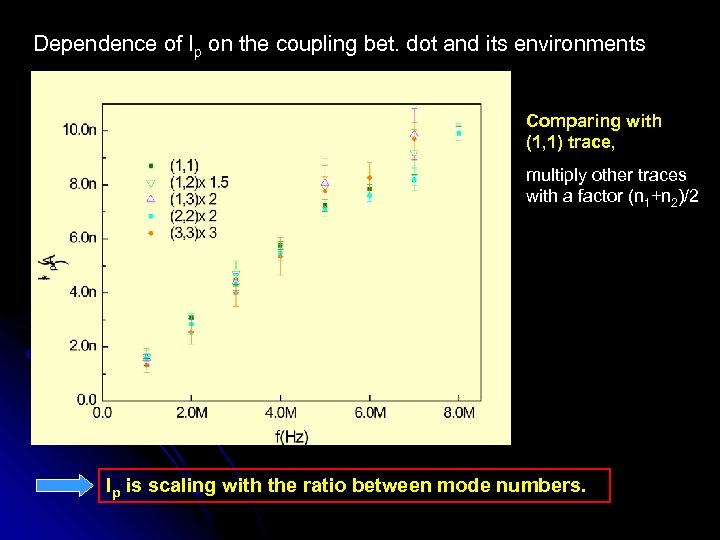
Dependence of Ip on the coupling bet. dot and its environments Comparing with (1, 1) trace, multiply other traces with a factor (n 1+n 2)/2 Ip is scaling with the ratio between mode numbers.

Why do n 1 and n 2 influence Ip? n 1 and n 2 are transmission mode numbers of both “entrance” leads of the “open” dot, respectively. Ø For the larger mode number, electrons have stronger coupling strength between dot and reservoirs. The escaping rate of electron in the dot Ø The escaping rate esc increases with mode number linearly, and electrons are more likely to escape to the reservoirs. With shorter dwell time, the coherent effect is reduced. Therefore, quantum pumping is suppressed w/. increasing Ntot.

Summary The dc current characteristics of pumping and rectification effects are drastically different in our systems. The pumping current decreases with increasing transmission mode numbers of the two QPCs due to the dephasing of the coherent electrons in the dot by rapid motions of entering and leaving the dot. The observed DC current in the pumping mode is mainly from the pumping effect. symmetric arrangement of pumping gates relative to both entrance leads of the dot

Acknowledgments: Dr. C. S. Chu (Theoretical support) Dr. V. Umansky (High mobility 2 DEG support)
