 С Т А Т И С Т И К А Социальноэкономическая статистика Промышленная другие и о к т р Общая теория и Сельско т статистики а хозяй с (принципы, Медико- с и ственная методы) биологи л т ческая а е т в с ы е Народного Юридичес образования кая
С Т А Т И С Т И К А Социальноэкономическая статистика Промышленная другие и о к т р Общая теория и Сельско т статистики а хозяй с (принципы, Медико- с и ственная методы) биологи л т ческая а е т в с ы е Народного Юридичес образования кая
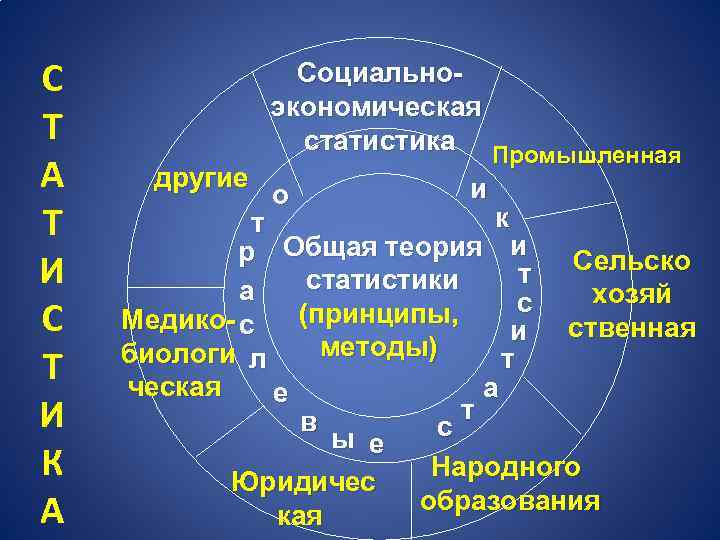
 Статистика самостоятельная общественная наука, изучающая количественную и качественную стороны массовых общественных явлений Медицинская (санитарная) статистика наука, занимающаяся изучением вопросов, связанных с медициной, гигиеной и общественным здоровьем, здравоохранением
Статистика самостоятельная общественная наука, изучающая количественную и качественную стороны массовых общественных явлений Медицинская (санитарная) статистика наука, занимающаяся изучением вопросов, связанных с медициной, гигиеной и общественным здоровьем, здравоохранением
 Статистика здоровья населения Изучает: • Здоровье населения в целом и его основных группах (численность и состав населения, его воспроизводство, физическое развитие, распространенность заболеваний, продолжительность жизни); • Выявление и установление связей заболеваемости и смертности населения с различными факторами окружающей среды
Статистика здоровья населения Изучает: • Здоровье населения в целом и его основных группах (численность и состав населения, его воспроизводство, физическое развитие, распространенность заболеваний, продолжительность жизни); • Выявление и установление связей заболеваемости и смертности населения с различными факторами окружающей среды
 Статистика здравоохранения Изучает: • Данные о сети ЛПУ и санитарных учреждений, их деятельность, кадры; • Оценка эффективности лечебнопрофилактических мероприятий; • Выявление закономерностей различий в здоровом и больном организме.
Статистика здравоохранения Изучает: • Данные о сети ЛПУ и санитарных учреждений, их деятельность, кадры; • Оценка эффективности лечебнопрофилактических мероприятий; • Выявление закономерностей различий в здоровом и больном организме.
 Статистический метод в клинических исследованиях Использованию математической статистики в медицине отведено особое место. Многие методы статистического анализа появились в статистике под влиянием медицинских и биологических научных разработок. Для обозначения особого статуса медикобиологической статистики введен термин биометрия
Статистический метод в клинических исследованиях Использованию математической статистики в медицине отведено особое место. Многие методы статистического анализа появились в статистике под влиянием медицинских и биологических научных разработок. Для обозначения особого статуса медикобиологической статистики введен термин биометрия
 Методика статистического исследования
Методика статистического исследования
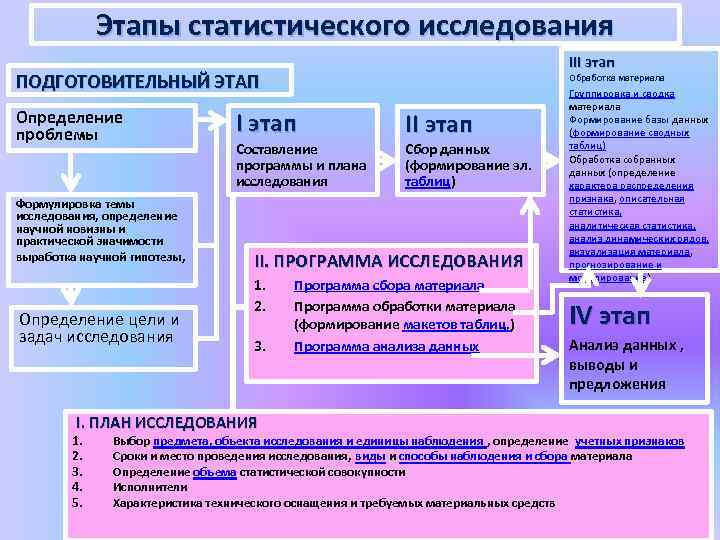 Этапы статистического исследования III этап ПОДГОТОВИТЕЛЬНЫЙ ЭТАП Определение проблемы Формулировка темы исследования, определение научной новизны и практической значимости выработка научной гипотезы, Определение цели и задач исследования I этап Составление программы и плана исследования II этап Сбор данных (формирование эл. таблиц) II. ПРОГРАММА ИССЛЕДОВАНИЯ 1. 2. 3. I. ПЛАН ИССЛЕДОВАНИЯ 1. 2. 3. 4. 5. Обработка материала Программа сбора материала Программа обработки материала (формирование макетов таблиц, ) Программа анализа данных Группировка и сводка материала Формирование базы данных (формирование сводных таблиц) Обработка собранных данных (определение характера распределения признака, описательная статистика, аналитическая статистика, анализ динамических рядов, визуализация материала, прогнозирование и моделирование) IV этап Анализ данных , выводы и предложения Выбор предмета, объекта исследования и единицы наблюдения , определение учетных признаков Сроки и место проведения исследования, виды и способы наблюдения и сбора материала Определение объема статистической совокупности Исполнители Характеристика технического оснащения и требуемых материальных средств
Этапы статистического исследования III этап ПОДГОТОВИТЕЛЬНЫЙ ЭТАП Определение проблемы Формулировка темы исследования, определение научной новизны и практической значимости выработка научной гипотезы, Определение цели и задач исследования I этап Составление программы и плана исследования II этап Сбор данных (формирование эл. таблиц) II. ПРОГРАММА ИССЛЕДОВАНИЯ 1. 2. 3. I. ПЛАН ИССЛЕДОВАНИЯ 1. 2. 3. 4. 5. Обработка материала Программа сбора материала Программа обработки материала (формирование макетов таблиц, ) Программа анализа данных Группировка и сводка материала Формирование базы данных (формирование сводных таблиц) Обработка собранных данных (определение характера распределения признака, описательная статистика, аналитическая статистика, анализ динамических рядов, визуализация материала, прогнозирование и моделирование) IV этап Анализ данных , выводы и предложения Выбор предмета, объекта исследования и единицы наблюдения , определение учетных признаков Сроки и место проведения исследования, виды и способы наблюдения и сбора материала Определение объема статистической совокупности Исполнители Характеристика технического оснащения и требуемых материальных средств
 Программа сбора материала КАРТА изучения заболеваемости с временной утратой трудоспособности металлургов Ф. И. О. ________________ пол ____________ возраст _____ образование _______ место работы _____________ специальность _______ общий стаж _____ профессиональный стаж ___________ диагноз _______ Дата выдачи больничного листка __________________ Дата выписки на работу ______________________ Социально-трудовые условия __________________________________________________________________ Социально-бытовая характеристика _________________________________________________ Дата заполнения карты ______________________
Программа сбора материала КАРТА изучения заболеваемости с временной утратой трудоспособности металлургов Ф. И. О. ________________ пол ____________ возраст _____ образование _______ место работы _____________ специальность _______ общий стаж _____ профессиональный стаж ___________ диагноз _______ Дата выдачи больничного листка __________________ Дата выписки на работу ______________________ Социально-трудовые условия __________________________________________________________________ Социально-бытовая характеристика _________________________________________________ Дата заполнения карты ______________________
 Программа обработки материала Групповая таблица Территории Уровень травматизма (в‰) Террито рия Район 1 Возраст (лет) Пол Муж Жен До 30 30 -49 50 и Район 1 Район 2 Всего: Комбинационная таблица Мужчины Травматизм в районе 1 Изолированные травмы Множественные травмы Сочетанные травмы Всего: До 40 лет 41 и более лет Женщины До 40 лет 41 и более лет Итого: Итого Простая таблица
Программа обработки материала Групповая таблица Территории Уровень травматизма (в‰) Террито рия Район 1 Возраст (лет) Пол Муж Жен До 30 30 -49 50 и Район 1 Район 2 Всего: Комбинационная таблица Мужчины Травматизм в районе 1 Изолированные травмы Множественные травмы Сочетанные травмы Всего: До 40 лет 41 и более лет Женщины До 40 лет 41 и более лет Итого: Итого Простая таблица
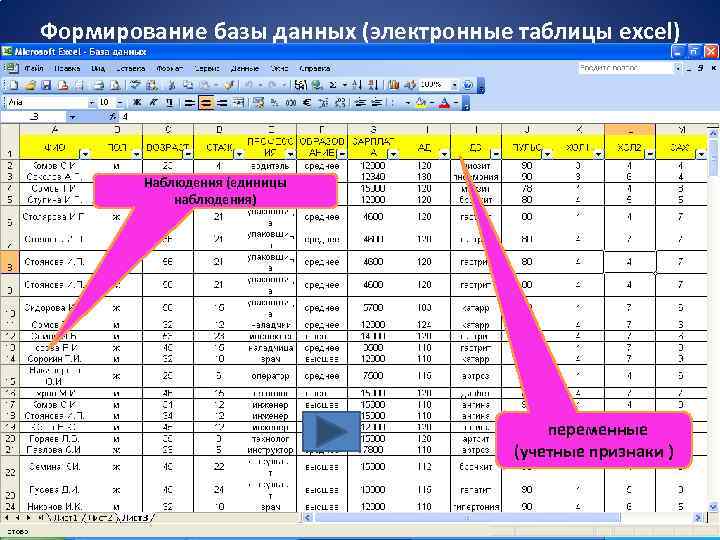 Формирование базы данных (электронные таблицы excel) Наблюдения (единицы наблюдения) переменные (учетные признаки )
Формирование базы данных (электронные таблицы excel) Наблюдения (единицы наблюдения) переменные (учетные признаки )
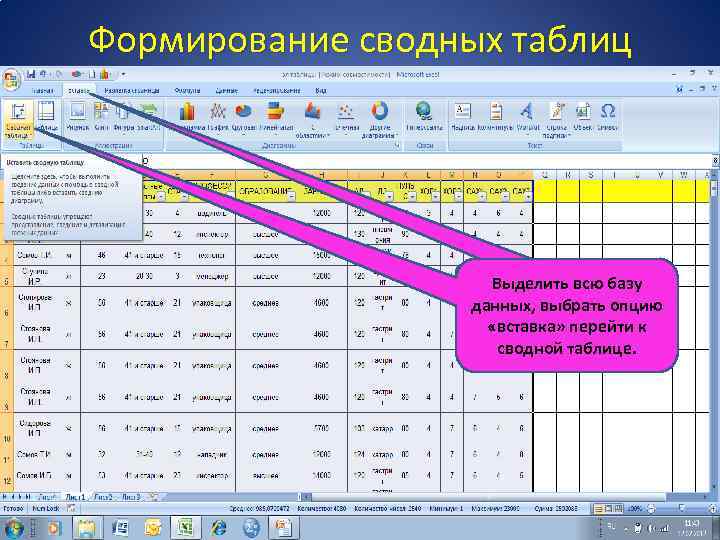 Формирование сводных таблиц Выделить всю базу данных, выбрать опцию «вставка» перейти к сводной таблице.
Формирование сводных таблиц Выделить всю базу данных, выбрать опцию «вставка» перейти к сводной таблице.
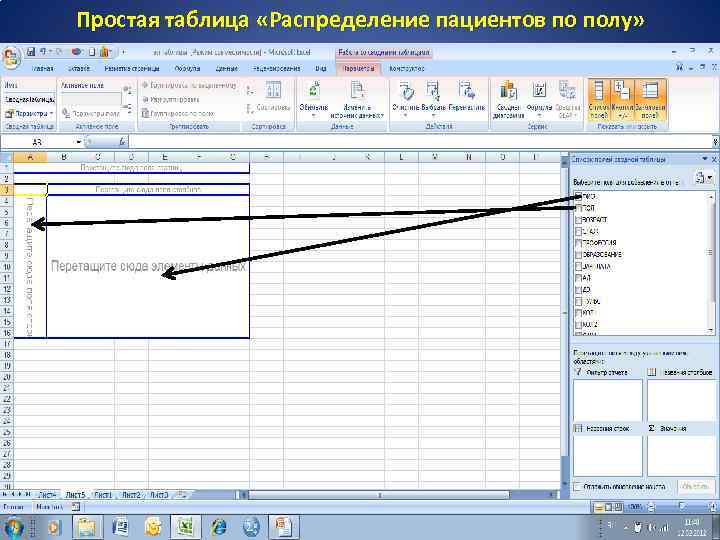 Простая таблица «Распределение пациентов по полу»
Простая таблица «Распределение пациентов по полу»
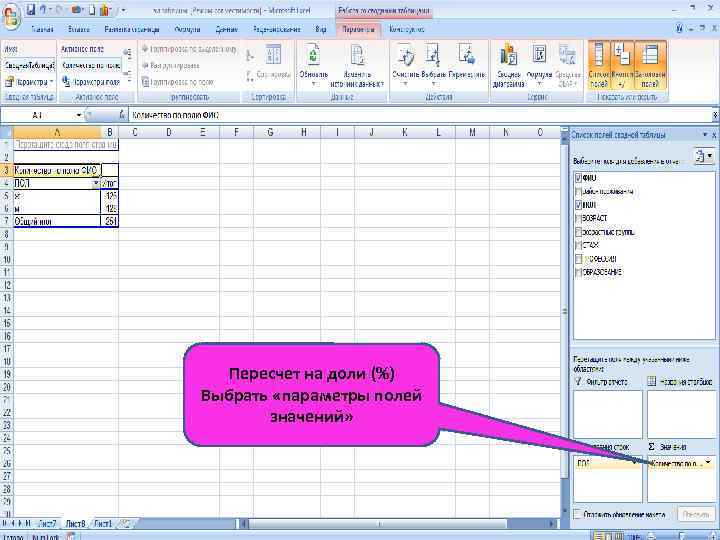 Простая таблица Пересчет на доли (%) Выбрать «параметры полей значений»
Простая таблица Пересчет на доли (%) Выбрать «параметры полей значений»
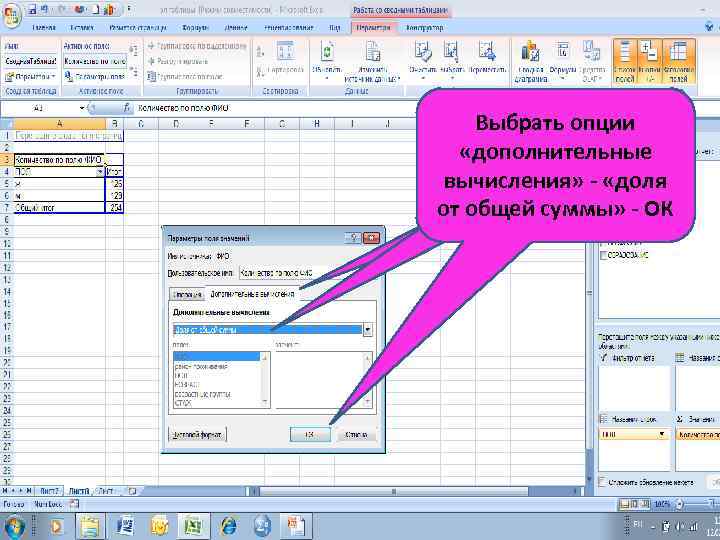 Выбрать опции «дополнительные вычисления» - «доля от общей суммы» - ОК
Выбрать опции «дополнительные вычисления» - «доля от общей суммы» - ОК
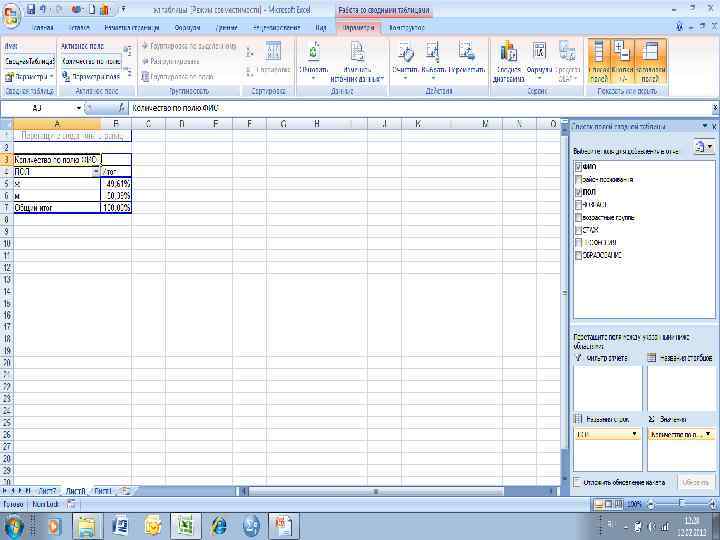
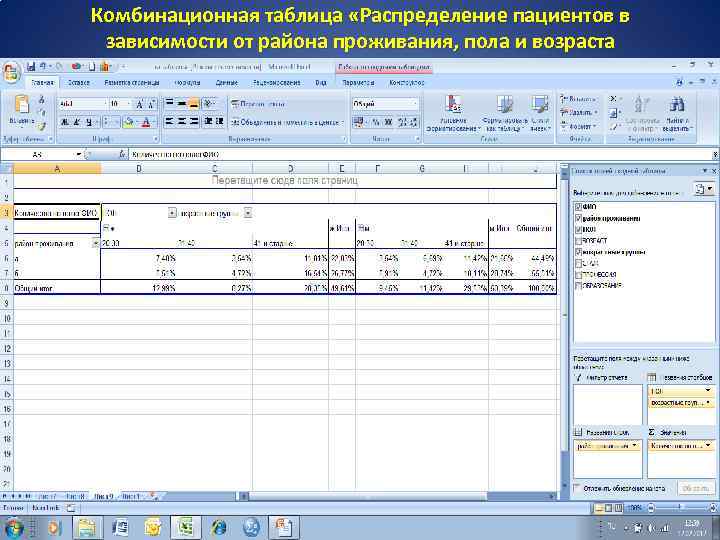 Комбинационная таблица «Распределение пациентов в зависимости от района проживания, пола и возраста
Комбинационная таблица «Распределение пациентов в зависимости от района проживания, пола и возраста
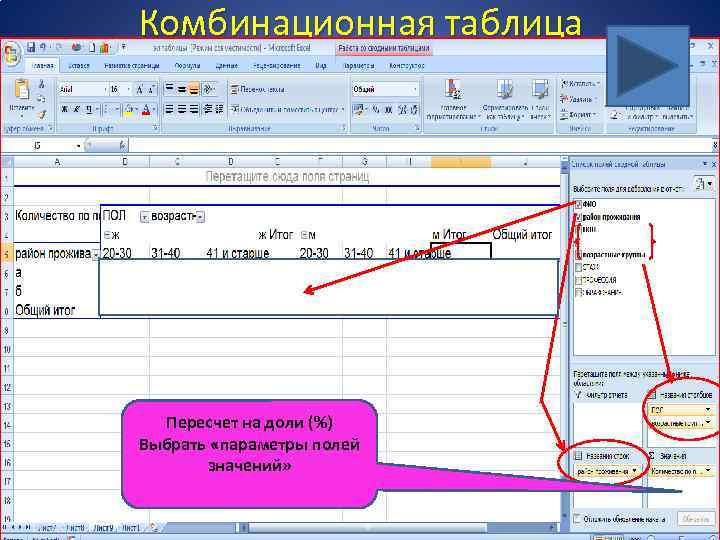 Комбинационная таблица Пересчет на доли (%) Выбрать «параметры полей значений»
Комбинационная таблица Пересчет на доли (%) Выбрать «параметры полей значений»
 Программа анализа материала Свойства статистической совокупности 1. – распределение признаков (абсолютные числа, относительные показатели); 2. – средний уровень признаков (средние величины, мода, медиана, интенсивные показатели); 3. – вариабельность – разнообразие признаков ( интерпроцентильный, интерквартильный размах, среднее квадратическое отклонение, коэффициент вариации); 4. – репрезентативность – представительность признаков (ошибки показателей, доверительные интервалы); 5. – корреляция признаков (коэффициенты корреляции (ассоциации), корреляционное отношение, регрессия)
Программа анализа материала Свойства статистической совокупности 1. – распределение признаков (абсолютные числа, относительные показатели); 2. – средний уровень признаков (средние величины, мода, медиана, интенсивные показатели); 3. – вариабельность – разнообразие признаков ( интерпроцентильный, интерквартильный размах, среднее квадратическое отклонение, коэффициент вариации); 4. – репрезентативность – представительность признаков (ошибки показателей, доверительные интервалы); 5. – корреляция признаков (коэффициенты корреляции (ассоциации), корреляционное отношение, регрессия)
 Репрезентативность Качественная Количественная Основана на законе вероятности и означает соответствие (однотипность) признаков, характеризующих элементы выборочной совокупности по отношению к генеральной Основана на законе больших чисел. Означает достаточную численность элементов выборочной совокупности, рассчитываемую по специальным формулам и таблицам
Репрезентативность Качественная Количественная Основана на законе вероятности и означает соответствие (однотипность) признаков, характеризующих элементы выборочной совокупности по отношению к генеральной Основана на законе больших чисел. Означает достаточную численность элементов выборочной совокупности, рассчитываемую по специальным формулам и таблицам
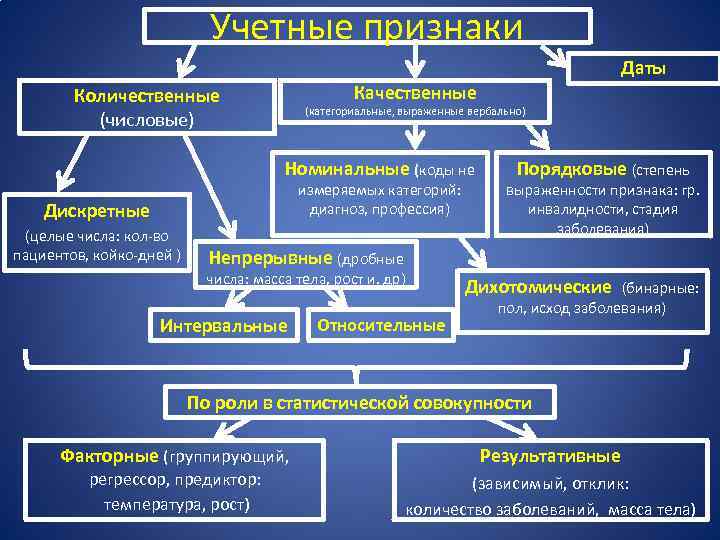 Учетные признаки Даты Качественные Количественные (числовые) (категориальные, выраженные вербально) Номинальные (коды не измеряемых категорий: диагноз, профессия) Дискретные (целые числа: кол-во пациентов, койко-дней ) Порядковые (степень выраженности признака: гр. инвалидности, стадия заболевания) Непрерывные (дробные числа: масса тела, рост и. др) Интервальные Относительные Дихотомические (бинарные: пол, исход заболевания) По роли в статистической совокупности Факторные (группирующий, регрессор, предиктор: температура, рост) Результативные (зависимый, отклик: количество заболеваний, масса тела)
Учетные признаки Даты Качественные Количественные (числовые) (категориальные, выраженные вербально) Номинальные (коды не измеряемых категорий: диагноз, профессия) Дискретные (целые числа: кол-во пациентов, койко-дней ) Порядковые (степень выраженности признака: гр. инвалидности, стадия заболевания) Непрерывные (дробные числа: масса тела, рост и. др) Интервальные Относительные Дихотомические (бинарные: пол, исход заболевания) По роли в статистической совокупности Факторные (группирующий, регрессор, предиктор: температура, рост) Результативные (зависимый, отклик: количество заболеваний, масса тела)
 Объем наблюдений должен быть достаточным для получения статистически значимых результатов, т. е. исследование должно иметь необходимую статистическую мощность • Таблица «Число наблюдений, необходимое для того, чтобы ошибка в 19 случаях из 20 не превысила заданного предела» • Номограмма Альтмана • Формулы для расчёта необходимого объема наблюдений • Необходимый объем наблюдений и мощность можно рассчитать в программе STATISTICA.
Объем наблюдений должен быть достаточным для получения статистически значимых результатов, т. е. исследование должно иметь необходимую статистическую мощность • Таблица «Число наблюдений, необходимое для того, чтобы ошибка в 19 случаях из 20 не превысила заданного предела» • Номограмма Альтмана • Формулы для расчёта необходимого объема наблюдений • Необходимый объем наблюдений и мощность можно рассчитать в программе STATISTICA.
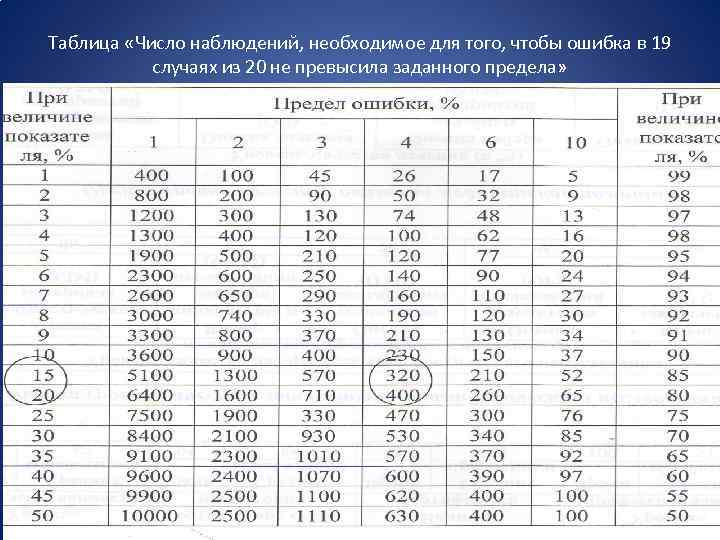 Таблица «Число наблюдений, необходимое для того, чтобы ошибка в 19 случаях из 20 не превысила заданного предела»
Таблица «Число наблюдений, необходимое для того, чтобы ошибка в 19 случаях из 20 не превысила заданного предела»
 Определение необходимого объема наблюдений выборочной совокупности t – доверительный коэффициент, p – показатель, n – число наблюдений, s – среднеквадратическое отклонение ∆ – предельная ошибка Для непарного критерия Стьюдента и критерия χ2 Пирсона для расчета объема выборки можно применить формулу Лера: 16/(стандартизованная разность) 2 = 16/(0, 50) 2 = 64. Числитель 16 относится к мощности 80%, а числитель 21 – к мощности 90%.
Определение необходимого объема наблюдений выборочной совокупности t – доверительный коэффициент, p – показатель, n – число наблюдений, s – среднеквадратическое отклонение ∆ – предельная ошибка Для непарного критерия Стьюдента и критерия χ2 Пирсона для расчета объема выборки можно применить формулу Лера: 16/(стандартизованная разность) 2 = 16/(0, 50) 2 = 64. Числитель 16 относится к мощности 80%, а числитель 21 – к мощности 90%.
 Проведем проверку достаточности объема наблюдений выборочной совокупности. Условия: t (критерий значимости) при p (уровень статистической значимости) - 95, 5% равен 2; Р (относительная частота явления) -16, 7. 5 - предельная ошибка выборки (задает сам исследователь)
Проведем проверку достаточности объема наблюдений выборочной совокупности. Условия: t (критерий значимости) при p (уровень статистической значимости) - 95, 5% равен 2; Р (относительная частота явления) -16, 7. 5 - предельная ошибка выборки (задает сам исследователь)
 • Проведем проверку достаточности объема наблюдений выборочной совокупности. Условие: t – доверительный коэффициент при = 95, 5% равен 2, • М (s)=58, 6 (1, 8) см; • ∆= 0, 5 см (задает сам исследователь) Следовательно, необходимый объем наблюдений выборочной совокупности равен 52.
• Проведем проверку достаточности объема наблюдений выборочной совокупности. Условие: t – доверительный коэффициент при = 95, 5% равен 2, • М (s)=58, 6 (1, 8) см; • ∆= 0, 5 см (задает сам исследователь) Следовательно, необходимый объем наблюдений выборочной совокупности равен 52.
 Способы сбора материала • По времени исследование может быть текущим и единовременным. • • Данные могут быть получены: Методом непосредственного наблюдения Методом выкопировки (извлечения) Анамнестическим методом Анкетный способом Способом интервьюирования Сочетание всех методик
Способы сбора материала • По времени исследование может быть текущим и единовременным. • • Данные могут быть получены: Методом непосредственного наблюдения Методом выкопировки (извлечения) Анамнестическим методом Анкетный способом Способом интервьюирования Сочетание всех методик
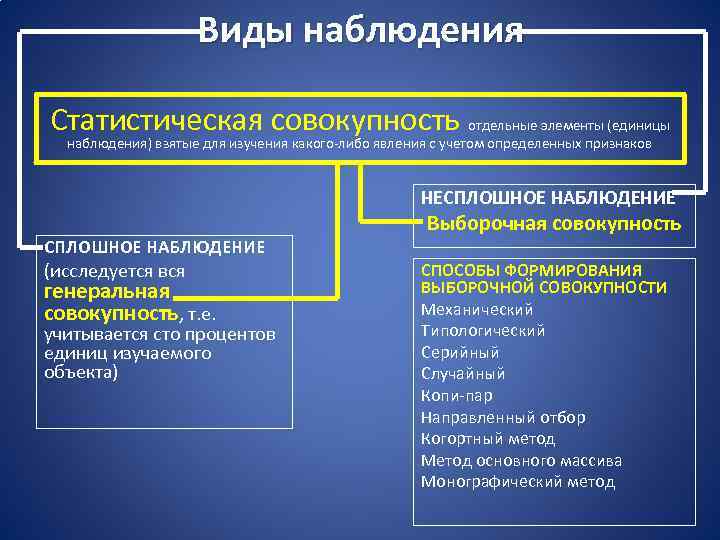 Виды наблюдения Статистическая совокупность отдельные элементы (единицы наблюдения) взятые для изучения какого-либо явления с учетом определенных признаков НЕСПЛОШНОЕ НАБЛЮДЕНИЕ (исследуется вся генеральная совокупность, т. е. учитывается сто процентов единиц изучаемого объекта) Выборочная совокупность СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ Механический Типологический Серийный Случайный Копи-пар Направленный отбор Когортный метод Метод основного массива Монографический метод
Виды наблюдения Статистическая совокупность отдельные элементы (единицы наблюдения) взятые для изучения какого-либо явления с учетом определенных признаков НЕСПЛОШНОЕ НАБЛЮДЕНИЕ (исследуется вся генеральная совокупность, т. е. учитывается сто процентов единиц изучаемого объекта) Выборочная совокупность СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ Механический Типологический Серийный Случайный Копи-пар Направленный отбор Когортный метод Метод основного массива Монографический метод
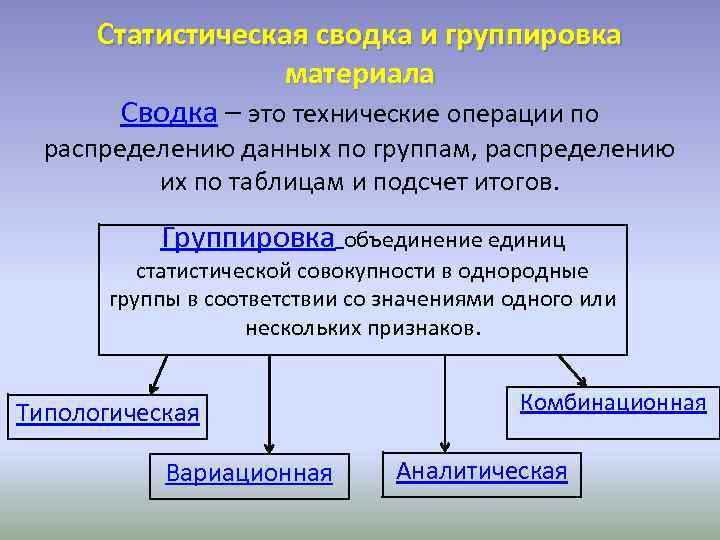 Статистическая сводка и группировка материала Сводка – это технические операции по распределению данных по группам, распределению их по таблицам и подсчет итогов. Группировка объединение единиц статистической совокупности в однородные группы в соответствии со значениями одного или нескольких признаков. Типологическая Вариационная Комбинационная Аналитическая
Статистическая сводка и группировка материала Сводка – это технические операции по распределению данных по группам, распределению их по таблицам и подсчет итогов. Группировка объединение единиц статистической совокупности в однородные группы в соответствии со значениями одного или нескольких признаков. Типологическая Вариационная Комбинационная Аналитическая
 Вариационная Число посещений Типологическая Кол-во обратившихся в % Пол Численность в % Мужчины 1 -2 Женщины 3 и более Итого Аналитическая Итого Статус Кол-во ед. набл. Уровень заболеваемости Курящие Некурящие Итого Комбинационная Состоят в браке Районы Не состоят в браке Возраст в годах До 20 лет 21 - 40 41 и более
Вариационная Число посещений Типологическая Кол-во обратившихся в % Пол Численность в % Мужчины 1 -2 Женщины 3 и более Итого Аналитическая Итого Статус Кол-во ед. набл. Уровень заболеваемости Курящие Некурящие Итого Комбинационная Состоят в браке Районы Не состоят в браке Возраст в годах До 20 лет 21 - 40 41 и более
 Предмет, объект исследования, единица наблюдения • Объект исследования - это статистическая совокупность, состоящая из относительно однородных отдельных предметов или явлений (единиц наблюдения), взятых вместе в известных границах времени и пространства. • Единица наблюдения (счетная единица) – составная часть, первичный элемент статистической совокупности, наделенный всеми признаками, подлежащими изучению и регистрации. • Предмет — это свойства, особенности, процессы объекта исследования, которые следует изучить. Это может быть явление в целом или отдельные стороны явления.
Предмет, объект исследования, единица наблюдения • Объект исследования - это статистическая совокупность, состоящая из относительно однородных отдельных предметов или явлений (единиц наблюдения), взятых вместе в известных границах времени и пространства. • Единица наблюдения (счетная единица) – составная часть, первичный элемент статистической совокупности, наделенный всеми признаками, подлежащими изучению и регистрации. • Предмет — это свойства, особенности, процессы объекта исследования, которые следует изучить. Это может быть явление в целом или отдельные стороны явления.
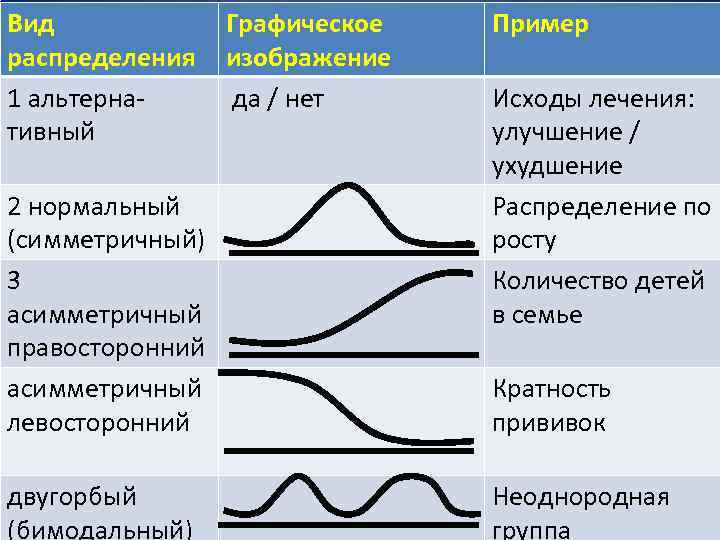 Вид распределения 1 альтернативный 2 нормальный (симметричный) 3 асимметричный правосторонний асимметричный левосторонний двугорбый (бимодальный) Графическое изображение да / нет Пример Исходы лечения: улучшение / ухудшение Распределение по росту Количество детей в семье Кратность прививок Неоднородная группа
Вид распределения 1 альтернативный 2 нормальный (симметричный) 3 асимметричный правосторонний асимметричный левосторонний двугорбый (бимодальный) Графическое изображение да / нет Пример Исходы лечения: улучшение / ухудшение Распределение по росту Количество детей в семье Кратность прививок Неоднородная группа
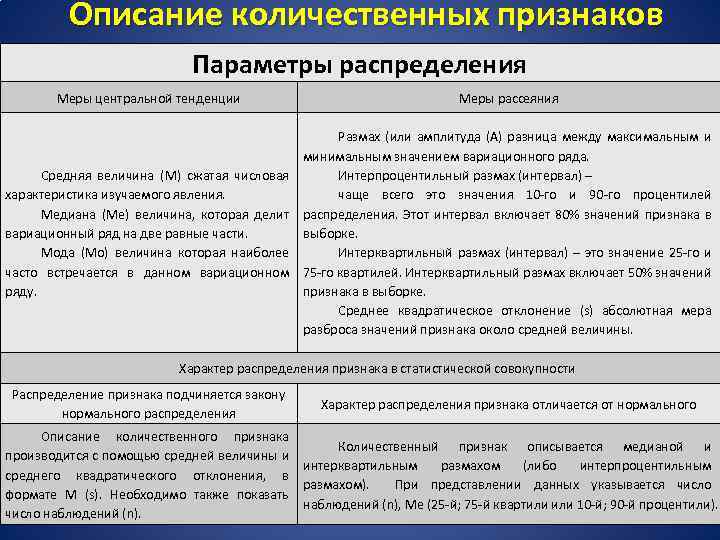 Описание количественных признаков Параметры распределения Меры центральной тенденции Меры рассеяния Средняя величина (М) сжатая числовая характеристика изучаемого явления. Медиана (Ме) величина, которая делит вариационный ряд на две равные части. Мода (Мо) величина которая наиболее часто встречается в данном вариационном ряду. Размах (или амплитуда (А) разница между максимальным и минимальным значением вариационного ряда. Интерпроцентильный размах (интервал) – чаще всего это значения 10 -го и 90 -го процентилей распределения. Этот интервал включает 80% значений признака в выборке. Интерквартильный размах (интервал) – это значение 25 -го и 75 -го квартилей. Интерквартильный размах включает 50% значений признака в выборке. Среднее квадратическое отклонение (s) абсолютная мера разброса значений признака около средней величины. Характер распределения признака в статистической совокупности Распределение признака подчиняется закону нормального распределения Характер распределения признака отличается от нормального Описание количественного признака Количественный признак описывается медианой и производится с помощью средней величины и интерквартильным размахом (либо интерпроцентильным среднего квадратического отклонения, в размахом). При представлении данных указывается число формате М (s). Необходимо также показать наблюдений (n), Ме (25 -й; 75 -й квартили 10 -й; 90 -й процентили). число наблюдений (n).
Описание количественных признаков Параметры распределения Меры центральной тенденции Меры рассеяния Средняя величина (М) сжатая числовая характеристика изучаемого явления. Медиана (Ме) величина, которая делит вариационный ряд на две равные части. Мода (Мо) величина которая наиболее часто встречается в данном вариационном ряду. Размах (или амплитуда (А) разница между максимальным и минимальным значением вариационного ряда. Интерпроцентильный размах (интервал) – чаще всего это значения 10 -го и 90 -го процентилей распределения. Этот интервал включает 80% значений признака в выборке. Интерквартильный размах (интервал) – это значение 25 -го и 75 -го квартилей. Интерквартильный размах включает 50% значений признака в выборке. Среднее квадратическое отклонение (s) абсолютная мера разброса значений признака около средней величины. Характер распределения признака в статистической совокупности Распределение признака подчиняется закону нормального распределения Характер распределения признака отличается от нормального Описание количественного признака Количественный признак описывается медианой и производится с помощью средней величины и интерквартильным размахом (либо интерпроцентильным среднего квадратического отклонения, в размахом). При представлении данных указывается число формате М (s). Необходимо также показать наблюдений (n), Ме (25 -й; 75 -й квартили 10 -й; 90 -й процентили). число наблюдений (n).
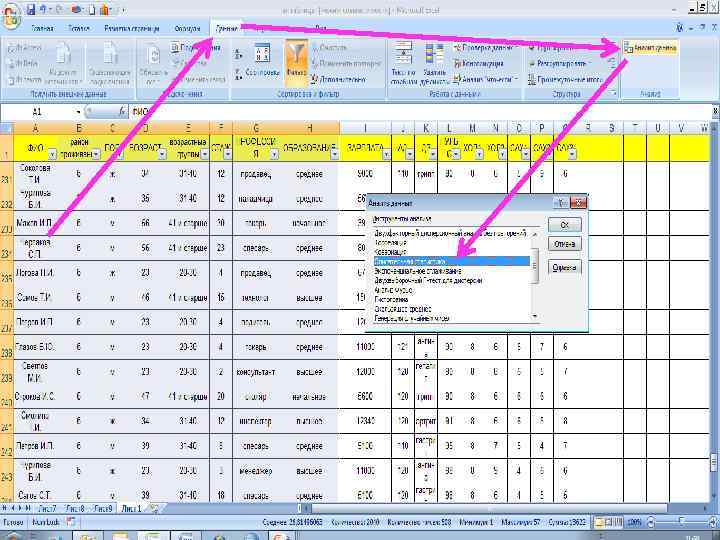
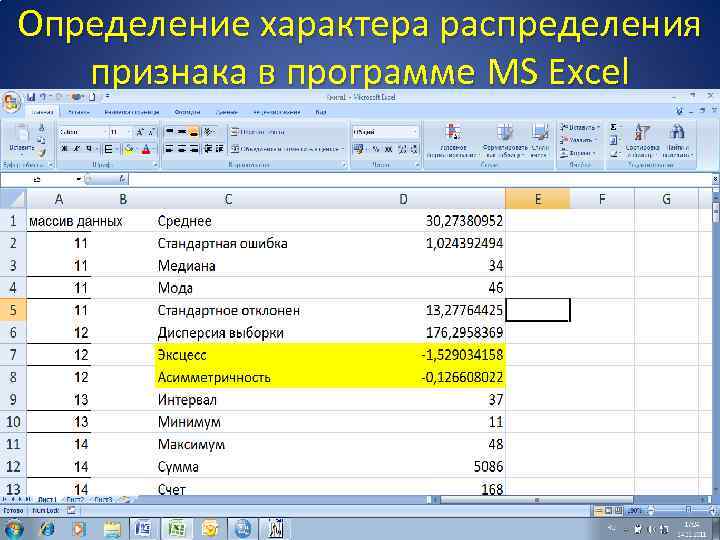 Определение характера распределения признака в программе MS Excel
Определение характера распределения признака в программе MS Excel
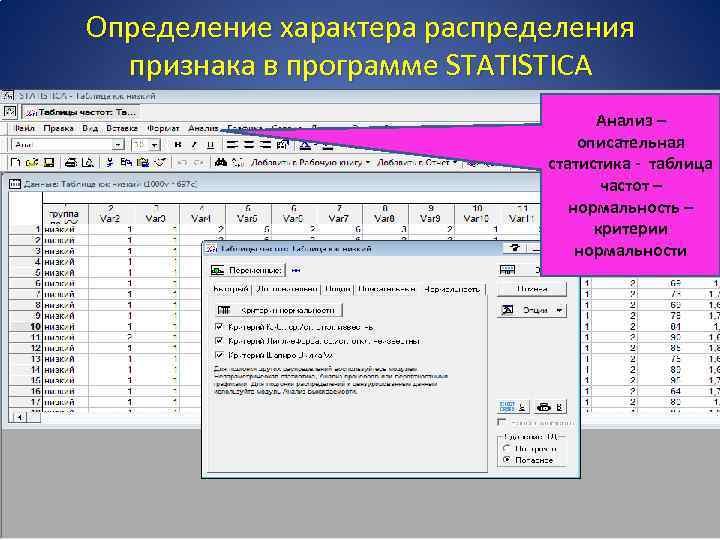 Определение характера распределения признака в программе STATISTICA Анализ – описательная статистика - таблица частот – нормальность – критерии нормальности
Определение характера распределения признака в программе STATISTICA Анализ – описательная статистика - таблица частот – нормальность – критерии нормальности
 Абсолютные показатели. Область применения • Для характеристики абсолютных размеров явления в целом (показывают массовость явления) • Для характеристики редко встречающихся явлений Относительные показатели. Область применения • Для определения уровня, частоты, распространенности того или иного явления; структуры явления • Для сравнения совокупностей по степени частоты того или иного явления; • Для выявления в динамике изменений степени частоты явления в наблюдаемой совокупности
Абсолютные показатели. Область применения • Для характеристики абсолютных размеров явления в целом (показывают массовость явления) • Для характеристики редко встречающихся явлений Относительные показатели. Область применения • Для определения уровня, частоты, распространенности того или иного явления; структуры явления • Для сравнения совокупностей по степени частоты того или иного явления; • Для выявления в динамике изменений степени частоты явления в наблюдаемой совокупности
 Виды относительных показателей • • Экстенсивные показатели Интенсивные показатели Показатели соотношения Показатели наглядности
Виды относительных показателей • • Экстенсивные показатели Интенсивные показатели Показатели соотношения Показатели наглядности
 Вычисление экстенсивного показателя показатель, характеризующий структуру явления, который выражается в % по отношению к итоговым данным Условие: Болезни органов дыхания О. бронхит Пневмония Б. астма Прочие Всего Решение: 25 чел. - 100% 5 чел. - х Кол-во случаев В% 5 10 20, 0% 40, 0% 5 5 25 20, 0% 100, 0% 5 х 100 х = -------- = 20%; и т. д. 25
Вычисление экстенсивного показателя показатель, характеризующий структуру явления, который выражается в % по отношению к итоговым данным Условие: Болезни органов дыхания О. бронхит Пневмония Б. астма Прочие Всего Решение: 25 чел. - 100% 5 чел. - х Кол-во случаев В% 5 10 20, 0% 40, 0% 5 5 25 20, 0% 100, 0% 5 х 100 х = -------- = 20%; и т. д. 25
 Вычисление интенсивного показателя Показатель частоты, который вычисляется на 100, 10000 в однородной среде. Интенсивный коэффициент заболеваемости (смертности) Число заболеваний (смертей) х 1000 _______________ = Средняя численность населения
Вычисление интенсивного показателя Показатель частоты, который вычисляется на 100, 10000 в однородной среде. Интенсивный коэффициент заболеваемости (смертности) Число заболеваний (смертей) х 1000 _______________ = Средняя численность населения
 Вычисление показателя соотношения показатель частоты, рассчитывается на 100, 10000 в разнородной среде. Условие: В районе Н. с численностью населения 40000 развернуто 480 больничных коек. Необходимо дать характеристику обеспеченности населения больничными койками Решение: 40000 – 480 1000 - Х 1000 х 480 40000 Х= = 12, 0
Вычисление показателя соотношения показатель частоты, рассчитывается на 100, 10000 в разнородной среде. Условие: В районе Н. с численностью населения 40000 развернуто 480 больничных коек. Необходимо дать характеристику обеспеченности населения больничными койками Решение: 40000 – 480 1000 - Х 1000 х 480 40000 Х= = 12, 0
 Вычисление показателя наглядности показатель, характеризующий динамику явления, вычисляется в % к начальному уровню или средней величине принятым за 100% Условие: годы Обеспеченность врачами Показатель наглядности Решение: 1980 1985 1990 30 33 35 100% 116, 6% Показатель обеспеченности врачами в 1980 г. принимаем за 100%, тогда обеспеченность врачами в 1985 г. составит: 30 – 100% 33 - х 33 х 100 х = -------- = 110% И Т. Д. 30
Вычисление показателя наглядности показатель, характеризующий динамику явления, вычисляется в % к начальному уровню или средней величине принятым за 100% Условие: годы Обеспеченность врачами Показатель наглядности Решение: 1980 1985 1990 30 33 35 100% 116, 6% Показатель обеспеченности врачами в 1980 г. принимаем за 100%, тогда обеспеченность врачами в 1985 г. составит: 30 – 100% 33 - х 33 х 100 х = -------- = 110% И Т. Д. 30
 Доверительный интервал 384 - 64 100 – Х m=± Х = 100 х 64 = 16, 7 384 16, 7 х (100 -16, 7) 384 95% ДИ 16, 7± 2 х 1, 9 Точечная оценка = ± 1, 9; (12, 9; 20, 5). Интервальная оценка (ДИ = Р±tm)
Доверительный интервал 384 - 64 100 – Х m=± Х = 100 х 64 = 16, 7 384 16, 7 х (100 -16, 7) 384 95% ДИ 16, 7± 2 х 1, 9 Точечная оценка = ± 1, 9; (12, 9; 20, 5). Интервальная оценка (ДИ = Р±tm)
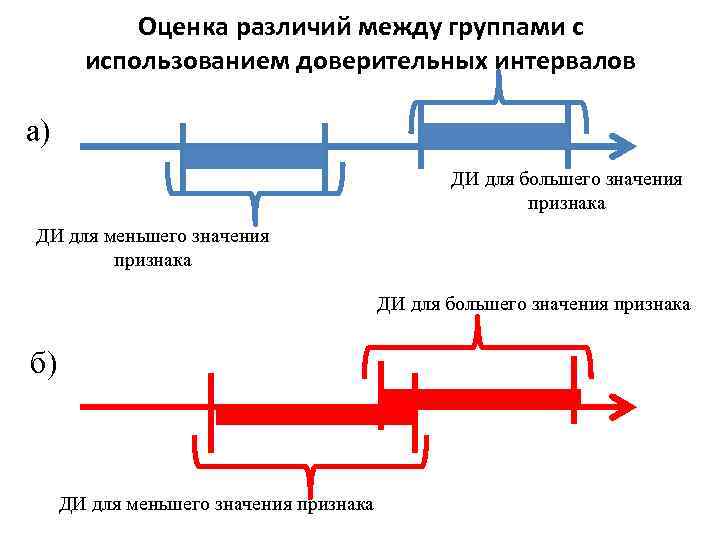 Оценка различий между группами с использованием доверительных интервалов а) ДИ для большего значения признака ДИ для меньшего значения признака ДИ для большего значения признака б) ДИ для меньшего значения признака
Оценка различий между группами с использованием доверительных интервалов а) ДИ для большего значения признака ДИ для меньшего значения признака ДИ для большего значения признака б) ДИ для меньшего значения признака
 Сравнение количественных признаков с помощью доверительных интервалов • Условие: М=58, 5 см. • 95% ДИ от 56, 7 см. до 60, 3 см. • Популяционное значение = 60, 0 см. • Вывод: 95%ДИ включает популяционное значение (60 см. ), следовательно, М в группе наблюдения не отличается от популяционных значений.
Сравнение количественных признаков с помощью доверительных интервалов • Условие: М=58, 5 см. • 95% ДИ от 56, 7 см. до 60, 3 см. • Популяционное значение = 60, 0 см. • Вывод: 95%ДИ включает популяционное значение (60 см. ), следовательно, М в группе наблюдения не отличается от популяционных значений.
 Для оценки различий групп путем проверки статистических гипотез необходимо: • 1. Какие группы сопоставляются (зависимые или независимые) • 2. Количество сравниваемых групп • 3. Учетные признаки (количественные или качественные) • 4. Характер распределения количественных признаков. • 5. Задача исследования.
Для оценки различий групп путем проверки статистических гипотез необходимо: • 1. Какие группы сопоставляются (зависимые или независимые) • 2. Количество сравниваемых групп • 3. Учетные признаки (количественные или качественные) • 4. Характер распределения количественных признаков. • 5. Задача исследования.
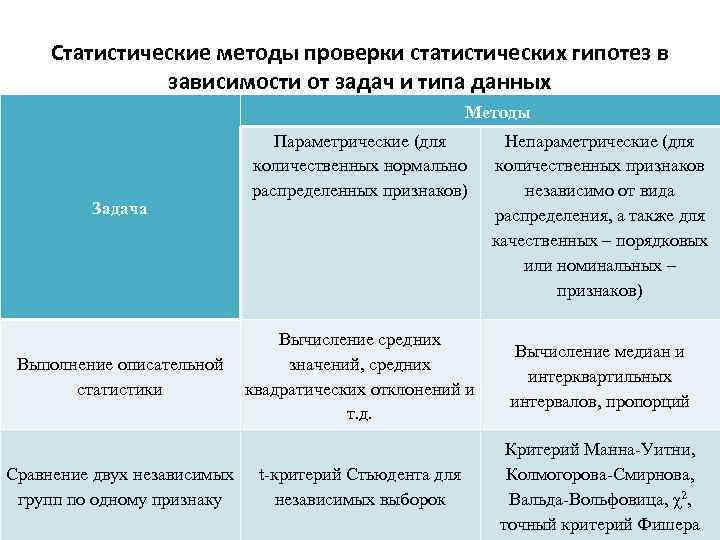 Статистические методы проверки статистических гипотез в зависимости от задач и типа данных Методы Задача Выполнение описательной статистики Сравнение двух независимых групп по одному признаку Параметрические (для количественных нормально распределенных признаков) Непараметрические (для количественных признаков независимо от вида распределения, а также для качественных – порядковых или номинальных – признаков) Вычисление средних значений, средних квадратических отклонений и т. д. Вычисление медиан и интерквартильных интервалов, пропорций t-критерий Стьюдента для независимых выборок Критерий Манна-Уитни, Колмогорова-Смирнова, Вальда-Вольфовица, χ2, точный критерий Фишера
Статистические методы проверки статистических гипотез в зависимости от задач и типа данных Методы Задача Выполнение описательной статистики Сравнение двух независимых групп по одному признаку Параметрические (для количественных нормально распределенных признаков) Непараметрические (для количественных признаков независимо от вида распределения, а также для качественных – порядковых или номинальных – признаков) Вычисление средних значений, средних квадратических отклонений и т. д. Вычисление медиан и интерквартильных интервалов, пропорций t-критерий Стьюдента для независимых выборок Критерий Манна-Уитни, Колмогорова-Смирнова, Вальда-Вольфовица, χ2, точный критерий Фишера
 Методы Статистические методы проверки статистических гипотез в зависимости Параметрические (для Непараметрические (для от задач и типа данных количественных нормально количественных признаков Задача распределенных признаков) независимо от вида распределения, а также для качественных – порядковых или номинальных – признаков) Сравнение двух зависимых групп по одному признаку t-критерий Стьюдента для зависимых выборок Критерий Вилкоксона, критерий знаков, критерий Мак. Немара Сравнение трех независимых групп и более по одному признаку Дисперсионный анализ (ANOVA) по Краскелу-Уоллису, медианный критерий, критерий χ2 Сравнение трех зависимых групп и более по одному признаку Критерий Кокрана ANOVA по Фридману, критерий Кокрана Анализ взаимосвязи двух признаков Корреляционный анализ по Пирсону Критерий χ2, корреляционный анализ по Спирмену, Кендаллу, гамма и др. Одновременный анализ трех признаков и более Регрессионнный анализ, дискриминантный анализ, факторный анализ, кластерный анализ Логистический регрессионный анализ, логлинейный анализ, анализ древовидных диаграмм, анализ конъюнкций и др.
Методы Статистические методы проверки статистических гипотез в зависимости Параметрические (для Непараметрические (для от задач и типа данных количественных нормально количественных признаков Задача распределенных признаков) независимо от вида распределения, а также для качественных – порядковых или номинальных – признаков) Сравнение двух зависимых групп по одному признаку t-критерий Стьюдента для зависимых выборок Критерий Вилкоксона, критерий знаков, критерий Мак. Немара Сравнение трех независимых групп и более по одному признаку Дисперсионный анализ (ANOVA) по Краскелу-Уоллису, медианный критерий, критерий χ2 Сравнение трех зависимых групп и более по одному признаку Критерий Кокрана ANOVA по Фридману, критерий Кокрана Анализ взаимосвязи двух признаков Корреляционный анализ по Пирсону Критерий χ2, корреляционный анализ по Спирмену, Кендаллу, гамма и др. Одновременный анализ трех признаков и более Регрессионнный анализ, дискриминантный анализ, факторный анализ, кластерный анализ Логистический регрессионный анализ, логлинейный анализ, анализ древовидных диаграмм, анализ конъюнкций и др.
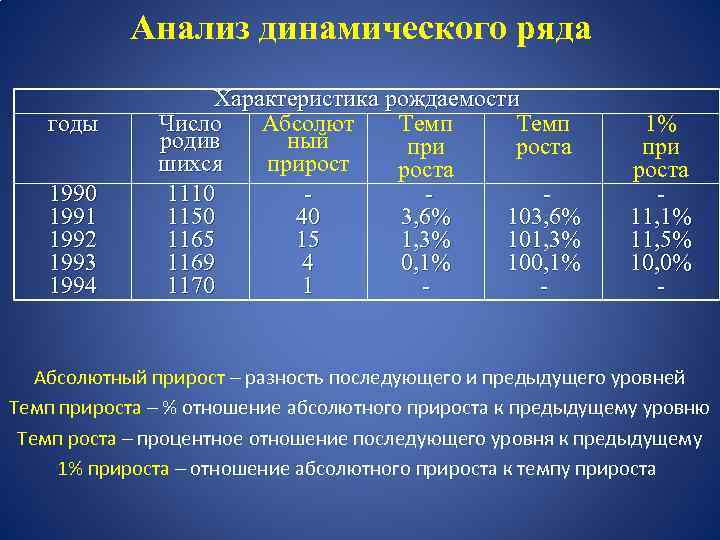 Анализ динамического ряда годы 1990 1991 1992 1993 1994 Характеристика рождаемости Число Абсолют Темп родив ный при роста шихся прироста 1110 1150 40 3, 6% 103, 6% 1165 15 1, 3% 101, 3% 1169 4 0, 1% 100, 1% 1170 1 - 1% при роста 11, 1% 11, 5% 10, 0% - Абсолютный прирост – разность последующего и предыдущего уровней Темп прироста – % отношение абсолютного прироста к предыдущему уровню Темп роста – процентное отношение последующего уровня к предыдущему 1% прироста – отношение абсолютного прироста к темпу прироста
Анализ динамического ряда годы 1990 1991 1992 1993 1994 Характеристика рождаемости Число Абсолют Темп родив ный при роста шихся прироста 1110 1150 40 3, 6% 103, 6% 1165 15 1, 3% 101, 3% 1169 4 0, 1% 100, 1% 1170 1 - 1% при роста 11, 1% 11, 5% 10, 0% - Абсолютный прирост – разность последующего и предыдущего уровней Темп прироста – % отношение абсолютного прироста к предыдущему уровню Темп роста – процентное отношение последующего уровня к предыдущему 1% прироста – отношение абсолютного прироста к темпу прироста
 Графические изображения 1. Диаграммы - изображение статистических данных при помощи линий и фигур • Линейные • Столбиковые • Фигурные • Радиальные • Внутристолбиковые • Секторные 2. Картограммы - изображение статистических данных на географических картах 3. Картодиаграммы – статистические данные изображаются в виде диаграмм на географической карте
Графические изображения 1. Диаграммы - изображение статистических данных при помощи линий и фигур • Линейные • Столбиковые • Фигурные • Радиальные • Внутристолбиковые • Секторные 2. Картограммы - изображение статистических данных на географических картах 3. Картодиаграммы – статистические данные изображаются в виде диаграмм на географической карте
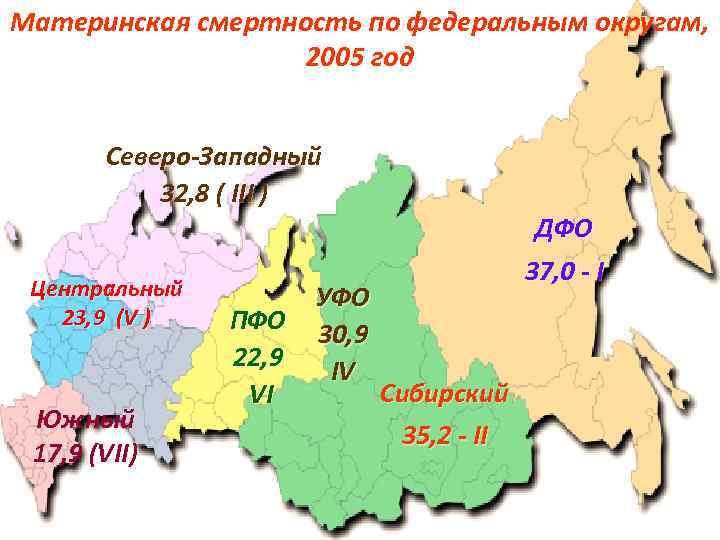 Материнская смертность по федеральным округам, 2005 год Северо-Западный 32, 8 ( III ) Центральный 23, 9 (V ) Южный 17, 9 (VII) ПФО 22, 9 VI УФО 30, 9 IV ДФО 37, 0 - I Сибирский 35, 2 - II
Материнская смертность по федеральным округам, 2005 год Северо-Западный 32, 8 ( III ) Центральный 23, 9 (V ) Южный 17, 9 (VII) ПФО 22, 9 VI УФО 30, 9 IV ДФО 37, 0 - I Сибирский 35, 2 - II
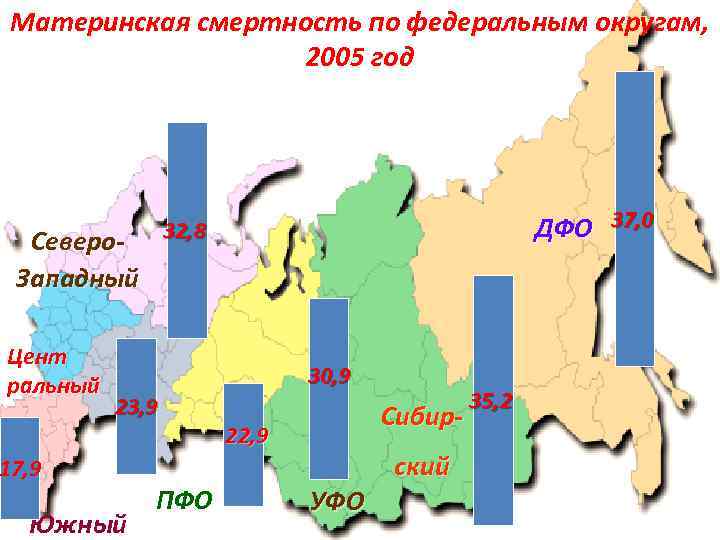 Материнская смертность по федеральным округам, 2005 год Северо. Западный Цент ральный 37, 0 ДФО 37, 0 32, 8 30, 9 23, 9 17, 9 Южный ПФО Сибир- 22, 9 ский УФО 35, 2
Материнская смертность по федеральным округам, 2005 год Северо. Западный Цент ральный 37, 0 ДФО 37, 0 32, 8 30, 9 23, 9 17, 9 Южный ПФО Сибир- 22, 9 ский УФО 35, 2
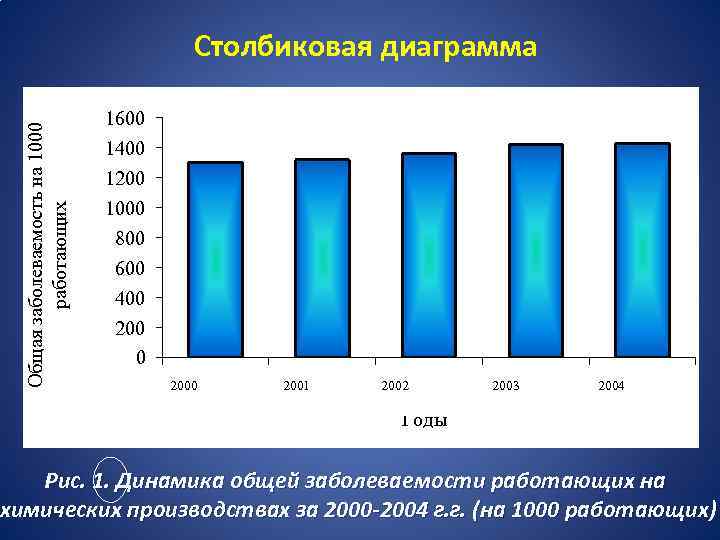 Общая заболеваемость на 1000 работающих Столбиковая диаграмма 1600 1400 1200 1000 800 600 400 2000 1 2001 2 2002 3 2003 4 2004 5 Годы Рис. 1. Динамика общей заболеваемости работающих на химических производствах за 2000 -2004 г. г. (на 1000 работающих)
Общая заболеваемость на 1000 работающих Столбиковая диаграмма 1600 1400 1200 1000 800 600 400 2000 1 2001 2 2002 3 2003 4 2004 5 Годы Рис. 1. Динамика общей заболеваемости работающих на химических производствах за 2000 -2004 г. г. (на 1000 работающих)
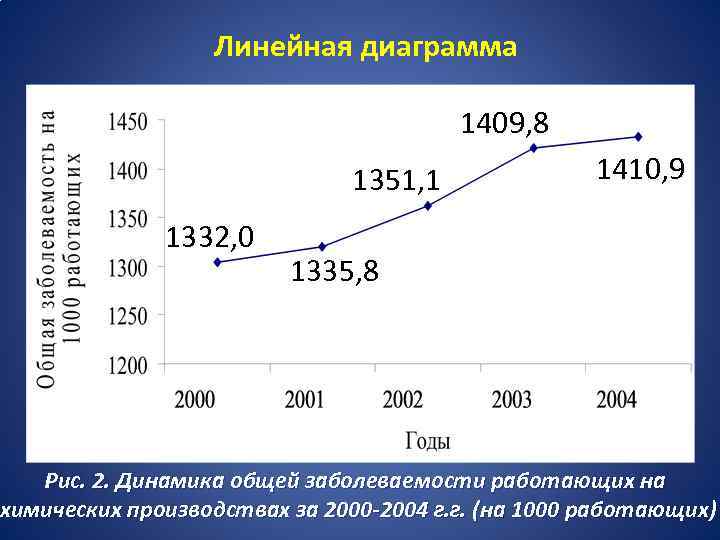 Линейная диаграмма 1409, 8 1351, 1 1332, 0 1410, 9 1335, 8 Рис. 2. Динамика общей заболеваемости работающих на химических производствах за 2000 -2004 г. г. (на 1000 работающих)
Линейная диаграмма 1409, 8 1351, 1 1332, 0 1410, 9 1335, 8 Рис. 2. Динамика общей заболеваемости работающих на химических производствах за 2000 -2004 г. г. (на 1000 работающих)
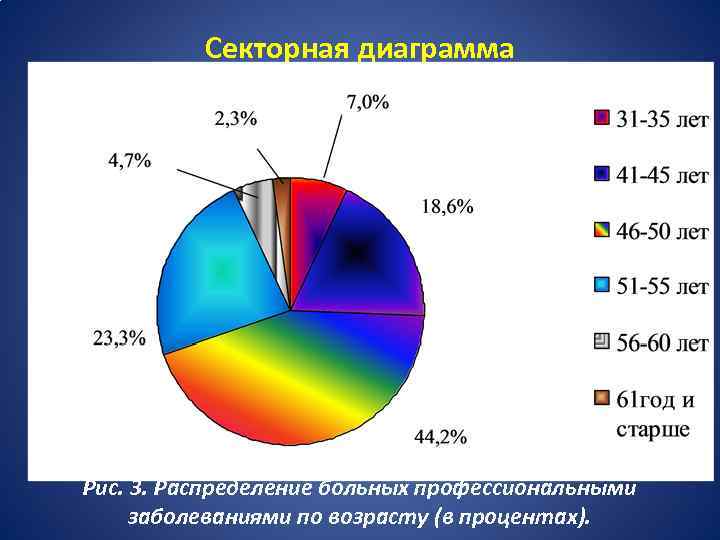 Секторная диаграмма Рис. 3. Распределение больных профессиональными заболеваниями по возрасту (в процентах).
Секторная диаграмма Рис. 3. Распределение больных профессиональными заболеваниями по возрасту (в процентах).
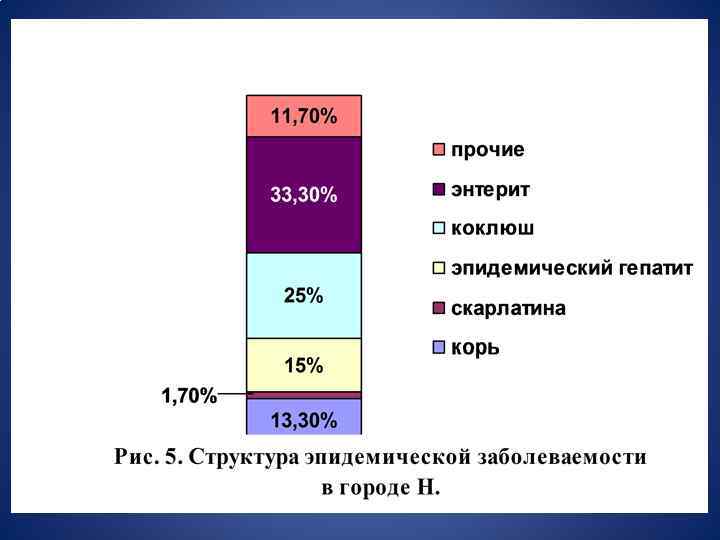
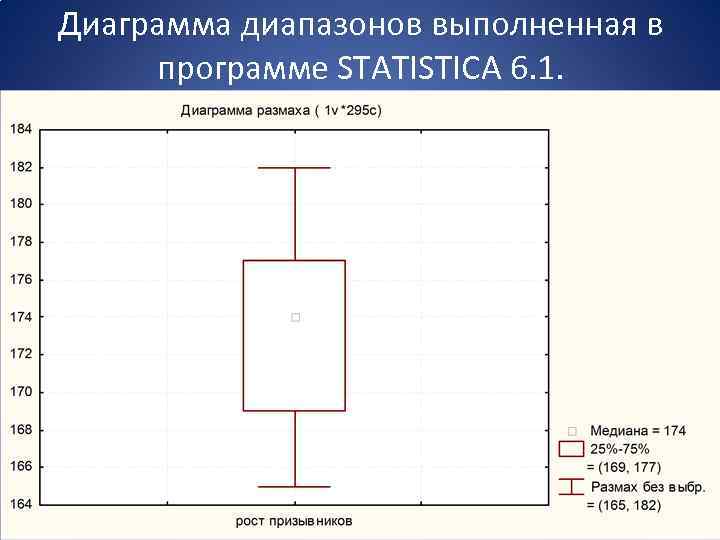 Диаграмма диапазонов выполненная в программе STATISTICA 6. 1.
Диаграмма диапазонов выполненная в программе STATISTICA 6. 1.
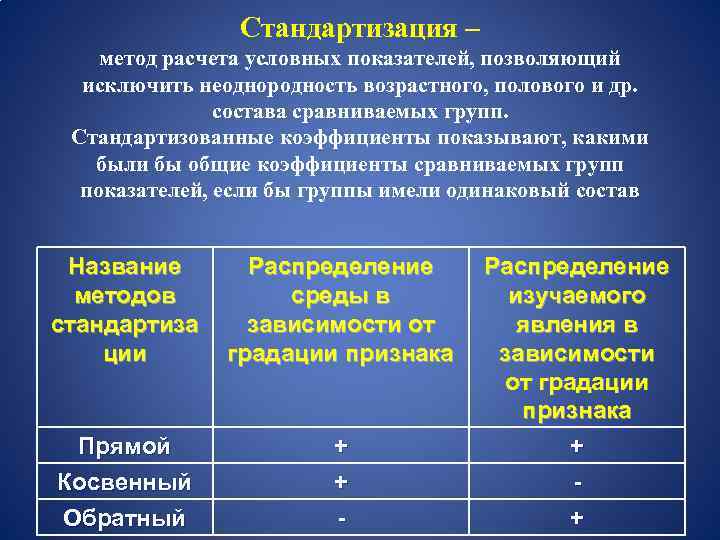 Стандартизация – метод расчета условных показателей, позволяющий исключить неоднородность возрастного, полового и др. состава сравниваемых групп. Стандартизованные коэффициенты показывают, какими были бы общие коэффициенты сравниваемых групп показателей, если бы группы имели одинаковый состав Название методов стандартиза ции Распределение среды в зависимости от градации признака Прямой Косвенный Обратный + + - Распределение изучаемого явления в зависимости от градации признака + +
Стандартизация – метод расчета условных показателей, позволяющий исключить неоднородность возрастного, полового и др. состава сравниваемых групп. Стандартизованные коэффициенты показывают, какими были бы общие коэффициенты сравниваемых групп показателей, если бы группы имели одинаковый состав Название методов стандартиза ции Распределение среды в зависимости от градации признака Прямой Косвенный Обратный + + - Распределение изучаемого явления в зависимости от градации признака + +
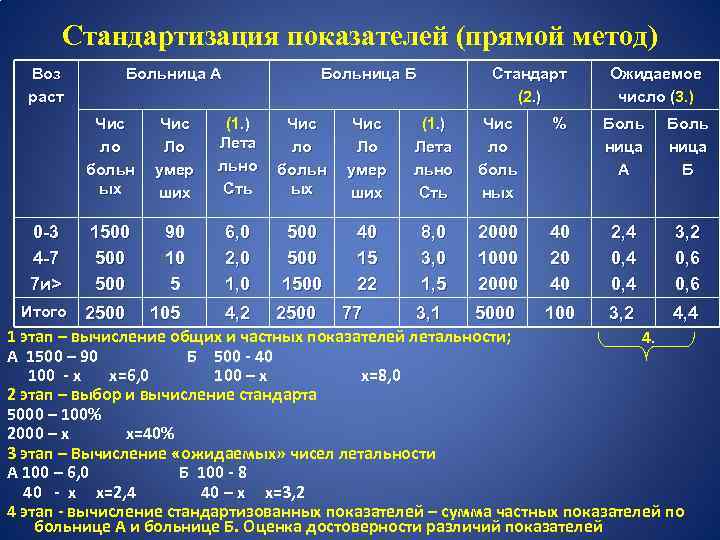 Стандартизация показателей (прямой метод) Воз раст Больница А Больница Б Стандарт (2. ) Ожидаемое число (3. ) ( Чис ло больн ых 0 -3 4 -7 7 и> Итого Чис Ло умер ших (1. ) Лета льно Сть Чис ло больн ых Чис Ло умер ших (1. ) Лета льно Сть Чис ло боль ных % Боль ница А Боль ница Б 1500 500 90 10 5 6, 0 2, 0 1, 0 500 1500 40 15 22 8, 0 3, 0 1, 5 2000 1000 2000 40 2, 4 0, 4 3, 2 0, 6 2500 105 4, 2 2500 77 3, 1 5000 100 3, 2 4, 4 1 этап – вычисление общих и частных показателей летальности; 4. А 1500 – 90 Б 500 - 40 100 - х х=6, 0 100 – х х=8, 0 2 этап – выбор и вычисление стандарта 5000 – 100% 2000 – х х=40% 3 этап – Вычисление «ожидаемых» чисел летальности А 100 – 6, 0 Б 100 - 8 40 - х х=2, 4 40 – х х=3, 2 4 этап - вычисление стандартизованных показателей – сумма частных показателей по больнице А и больнице Б. Оценка достоверности различий показателей
Стандартизация показателей (прямой метод) Воз раст Больница А Больница Б Стандарт (2. ) Ожидаемое число (3. ) ( Чис ло больн ых 0 -3 4 -7 7 и> Итого Чис Ло умер ших (1. ) Лета льно Сть Чис ло больн ых Чис Ло умер ших (1. ) Лета льно Сть Чис ло боль ных % Боль ница А Боль ница Б 1500 500 90 10 5 6, 0 2, 0 1, 0 500 1500 40 15 22 8, 0 3, 0 1, 5 2000 1000 2000 40 2, 4 0, 4 3, 2 0, 6 2500 105 4, 2 2500 77 3, 1 5000 100 3, 2 4, 4 1 этап – вычисление общих и частных показателей летальности; 4. А 1500 – 90 Б 500 - 40 100 - х х=6, 0 100 – х х=8, 0 2 этап – выбор и вычисление стандарта 5000 – 100% 2000 – х х=40% 3 этап – Вычисление «ожидаемых» чисел летальности А 100 – 6, 0 Б 100 - 8 40 - х х=2, 4 40 – х х=3, 2 4 этап - вычисление стандартизованных показателей – сумма частных показателей по больнице А и больнице Б. Оценка достоверности различий показателей
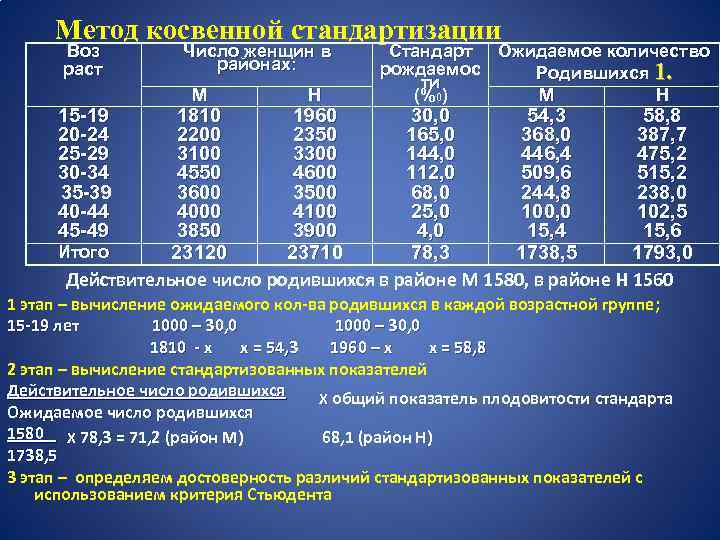 Метод косвенной стандартизации Воз раст 15 -19 20 -24 25 -29 30 -34 35 -39 40 -44 45 -49 Число женщин в районах: М Н Стандарт Ожидаемое количество рождаемос Родившихся 1. ти М Н (%0) 1810 1960 30, 0 54, 3 58, 8 2200 2350 165, 0 368, 0 387, 7 3100 3300 144, 0 446, 4 475, 2 4550 4600 112, 0 509, 6 515, 2 3600 3500 68, 0 244, 8 238, 0 4000 4100 25, 0 100, 0 102, 5 3850 3900 4, 0 15, 4 15, 6 Итого 23120 23710 78, 3 1738, 5 1793, 0 Действительное число родившихся в районе М 1580, в районе Н 1560 1 этап – вычисление ожидаемого кол-ва родившихся в каждой возрастной группе; 15 -19 лет 1000 – 30, 0 1810 - х х = 54, 3 1960 – х х = 58, 8 2 этап – вычисление стандартизованных показателей Действительное число родившихся Х общий показатель плодовитости стандарта Ожидаемое число родившихся 1580 Х 78, 3 = 71, 2 (район М) 68, 1 (район Н) 1738, 5 3 этап – определяем достоверность различий стандартизованных показателей с использованием критерия Стьюдента
Метод косвенной стандартизации Воз раст 15 -19 20 -24 25 -29 30 -34 35 -39 40 -44 45 -49 Число женщин в районах: М Н Стандарт Ожидаемое количество рождаемос Родившихся 1. ти М Н (%0) 1810 1960 30, 0 54, 3 58, 8 2200 2350 165, 0 368, 0 387, 7 3100 3300 144, 0 446, 4 475, 2 4550 4600 112, 0 509, 6 515, 2 3600 3500 68, 0 244, 8 238, 0 4000 4100 25, 0 100, 0 102, 5 3850 3900 4, 0 15, 4 15, 6 Итого 23120 23710 78, 3 1738, 5 1793, 0 Действительное число родившихся в районе М 1580, в районе Н 1560 1 этап – вычисление ожидаемого кол-ва родившихся в каждой возрастной группе; 15 -19 лет 1000 – 30, 0 1810 - х х = 54, 3 1960 – х х = 58, 8 2 этап – вычисление стандартизованных показателей Действительное число родившихся Х общий показатель плодовитости стандарта Ожидаемое число родившихся 1580 Х 78, 3 = 71, 2 (район М) 68, 1 (район Н) 1738, 5 3 этап – определяем достоверность различий стандартизованных показателей с использованием критерия Стьюдента
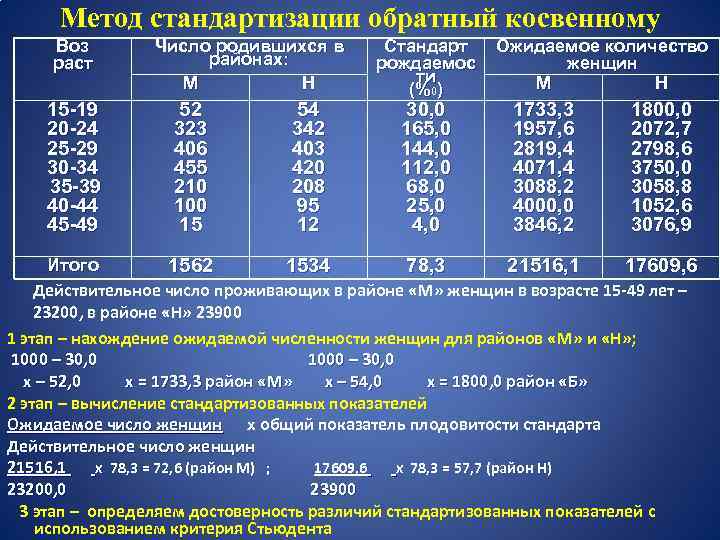 Метод стандартизации обратный косвенному Воз раст 15 -19 20 -24 25 -29 30 -34 35 -39 40 -44 45 -49 Число родившихся в районах: М Н 52 323 406 455 210 100 15 54 342 403 420 208 95 12 Стандарт рождаемос ти (%0) 30, 0 165, 0 144, 0 112, 0 68, 0 25, 0 4, 0 Ожидаемое количество женщин М Н 1733, 3 1957, 6 2819, 4 4071, 4 3088, 2 4000, 0 3846, 2 1800, 0 2072, 7 2798, 6 3750, 0 3058, 8 1052, 6 3076, 9 Итого 1562 1534 78, 3 21516, 1 17609, 6 Действительное число проживающих в районе «М» женщин в возрасте 15 -49 лет – 23200, в районе «Н» 23900 1 этап – нахождение ожидаемой численности женщин для районов «М» и «Н» ; 1000 – 30, 0 х – 52, 0 х = 1733, 3 район «М» х – 54, 0 х = 1800, 0 район «Б» 2 этап – вычисление стандартизованных показателей Ожидаемое число женщин х общий показатель плодовитости стандарта Действительное число женщин 21516, 1 х 78, 3 = 72, 6 (район М) ; 17609, 6 х 78, 3 = 57, 7 (район Н) 23200, 0 23900 3 этап – определяем достоверность различий стандартизованных показателей с использованием критерия Стьюдента
Метод стандартизации обратный косвенному Воз раст 15 -19 20 -24 25 -29 30 -34 35 -39 40 -44 45 -49 Число родившихся в районах: М Н 52 323 406 455 210 100 15 54 342 403 420 208 95 12 Стандарт рождаемос ти (%0) 30, 0 165, 0 144, 0 112, 0 68, 0 25, 0 4, 0 Ожидаемое количество женщин М Н 1733, 3 1957, 6 2819, 4 4071, 4 3088, 2 4000, 0 3846, 2 1800, 0 2072, 7 2798, 6 3750, 0 3058, 8 1052, 6 3076, 9 Итого 1562 1534 78, 3 21516, 1 17609, 6 Действительное число проживающих в районе «М» женщин в возрасте 15 -49 лет – 23200, в районе «Н» 23900 1 этап – нахождение ожидаемой численности женщин для районов «М» и «Н» ; 1000 – 30, 0 х – 52, 0 х = 1733, 3 район «М» х – 54, 0 х = 1800, 0 район «Б» 2 этап – вычисление стандартизованных показателей Ожидаемое число женщин х общий показатель плодовитости стандарта Действительное число женщин 21516, 1 х 78, 3 = 72, 6 (район М) ; 17609, 6 х 78, 3 = 57, 7 (район Н) 23200, 0 23900 3 этап – определяем достоверность различий стандартизованных показателей с использованием критерия Стьюдента
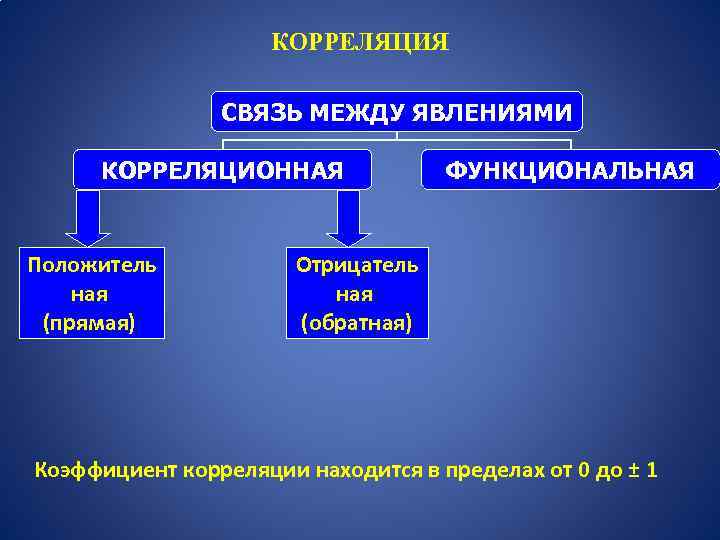 КОРРЕЛЯЦИЯ СВЯЗЬ МЕЖДУ ЯВЛЕНИЯМИ КОРРЕЛЯЦИОННАЯ Положитель ная (прямая) ФУНКЦИОНАЛЬНАЯ Отрицатель ная (обратная) Коэффициент корреляции находится в пределах от 0 до ± 1
КОРРЕЛЯЦИЯ СВЯЗЬ МЕЖДУ ЯВЛЕНИЯМИ КОРРЕЛЯЦИОННАЯ Положитель ная (прямая) ФУНКЦИОНАЛЬНАЯ Отрицатель ная (обратная) Коэффициент корреляции находится в пределах от 0 до ± 1
 Шкала Чеддока. Количественная мера тесноты связи Качественная характеристика силы связи 0, 1 -0, 3 Слабая 0, 3 -0, 5 Умеренная 0, 5 -0, 7 Заметная 0, 7 -0, 9 Высокая 0, 9 -0, 99 Весьма высокая
Шкала Чеддока. Количественная мера тесноты связи Качественная характеристика силы связи 0, 1 -0, 3 Слабая 0, 3 -0, 5 Умеренная 0, 5 -0, 7 Заметная 0, 7 -0, 9 Высокая 0, 9 -0, 99 Весьма высокая
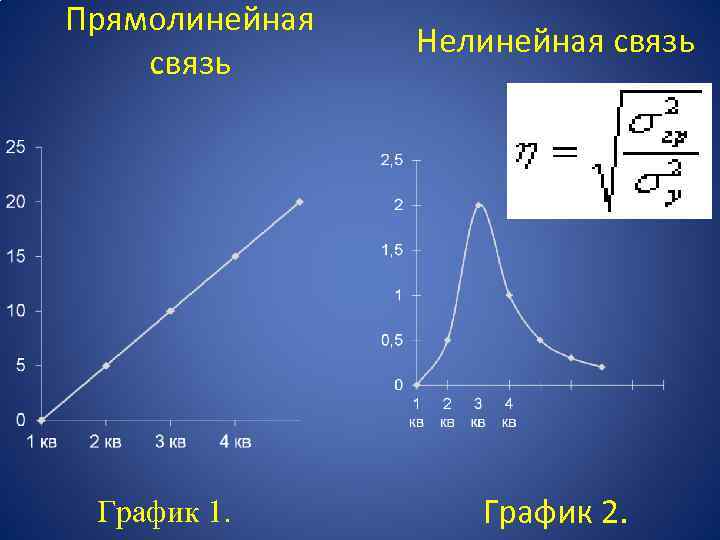 Прямолинейная связь График 1. Нелинейная связь График 2.
Прямолинейная связь График 1. Нелинейная связь График 2.
 Нелинейная связь
Нелинейная связь
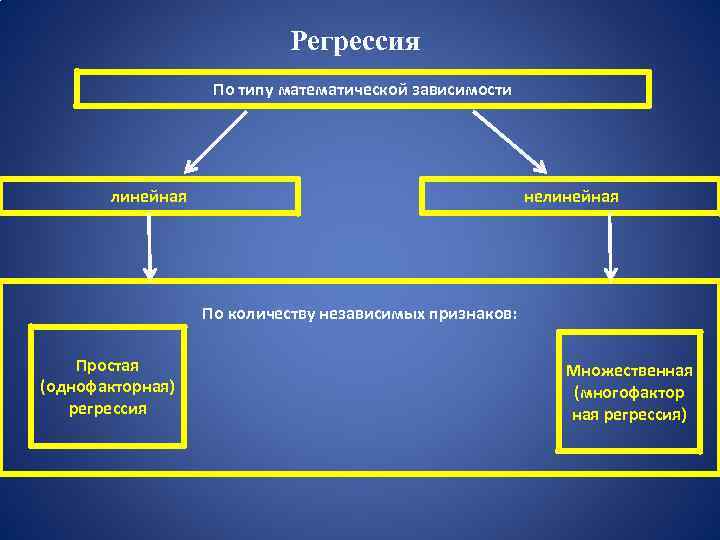 Регрессия По типу математической зависимости линейная нелинейная По количеству независимых признаков: Простая (однофакторная) регрессия Множественная (многофактор ная регрессия)
Регрессия По типу математической зависимости линейная нелинейная По количеству независимых признаков: Простая (однофакторная) регрессия Множественная (многофактор ная регрессия)
 НЕЛИНЕЙНАЯ РЕГРЕССИЯ вид: Уравнение регрессии в данном случае имеет где: • полином 2 степени у = а +bх + с2 + ε, • полином 3 степени у =а + bх +сх +dx 3+ ε, • у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х); Х — известная средняя величина другого признака; Ry/x — коэффициент регрессии; Мх, Му — известные средние величины признаков x и у. равносторонняя гипербола • степенная функция b y = aх ε l (n – количество независимых переменных; i – текущий номер рассматриваемой независимой переменной) показательная – у = аbх ε l экспоненциальная – y=ea+bxε
НЕЛИНЕЙНАЯ РЕГРЕССИЯ вид: Уравнение регрессии в данном случае имеет где: • полином 2 степени у = а +bх + с2 + ε, • полином 3 степени у =а + bх +сх +dx 3+ ε, • у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х); Х — известная средняя величина другого признака; Ry/x — коэффициент регрессии; Мх, Му — известные средние величины признаков x и у. равносторонняя гипербола • степенная функция b y = aх ε l (n – количество независимых переменных; i – текущий номер рассматриваемой независимой переменной) показательная – у = аbх ε l экспоненциальная – y=ea+bxε
 Проверка адекватности модели • Проверка значимости коэффициентов регрессии • Оценивание с использованием критерия Фишера • Оценивание с использованием коэффициента детерминации • Вычисление статистики Дарбина-Уотсона • Ошибка аппроксимации
Проверка адекватности модели • Проверка значимости коэффициентов регрессии • Оценивание с использованием критерия Фишера • Оценивание с использованием коэффициента детерминации • Вычисление статистики Дарбина-Уотсона • Ошибка аппроксимации
 Основные понятия регрессионного анализа Регрессия – это функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно с ним связанного.
Основные понятия регрессионного анализа Регрессия – это функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно с ним связанного.
 Коэффициент регрессии это абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого, на установленную единицу измерения. Коэффициент регрессии определяется по формуле: Rу/х = rху х (sу / sx), где Rу/х — коэффициент регрессии; rху — коэффициент корреляции между признаками х и у; sу и sx) — среднеквадратические отклонения признаков x и у.
Коэффициент регрессии это абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого, на установленную единицу измерения. Коэффициент регрессии определяется по формуле: Rу/х = rху х (sу / sx), где Rу/х — коэффициент регрессии; rху — коэффициент корреляции между признаками х и у; sу и sx) — среднеквадратические отклонения признаков x и у.
 Задача: Необходимо установить, как будет изменяться число острых респираторных заболеваний (У) при снижении среднемесячной температуры (Х) воздуха на 1 градус. R xy между изменениями среднемесячной температуры в зимний период (х) r = - 0, 7; и средним числом острых респираторных заболеваний (у) ху р=0, 052 sх = 6, 3 (среднеквадратическое отклонение температуры воздуха в зимний период; sу = 20, 9 (среднеквадратическое отклонение числа острых респираторных заболеваний) В этом случае коэффициент регрессии: Rу/х = -0, 7 х (20, 9 / 6, 3) = 2, 3.
Задача: Необходимо установить, как будет изменяться число острых респираторных заболеваний (У) при снижении среднемесячной температуры (Х) воздуха на 1 градус. R xy между изменениями среднемесячной температуры в зимний период (х) r = - 0, 7; и средним числом острых респираторных заболеваний (у) ху р=0, 052 sх = 6, 3 (среднеквадратическое отклонение температуры воздуха в зимний период; sу = 20, 9 (среднеквадратическое отклонение числа острых респираторных заболеваний) В этом случае коэффициент регрессии: Rу/х = -0, 7 х (20, 9 / 6, 3) = 2, 3.
 Уравнение регрессии в случае прямолинейной связи между двумя признаками (х и у) имеет вид у = Му + Ry/x (х - Мx), где: у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х); х — известная средняя величина другого признака; Ry/x — коэффициент регрессии; Мх, Му — известные средние величины признаков x и у.
Уравнение регрессии в случае прямолинейной связи между двумя признаками (х и у) имеет вид у = Му + Ry/x (х - Мx), где: у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х); х — известная средняя величина другого признака; Ry/x — коэффициент регрессии; Мх, Му — известные средние величины признаков x и у.
 Необходимо определить среднее число острых респираторных заболеваний при температуре 25°. х = -25° Rу/х = 2, 3 заболевания. Мх = -23° Му = 34 случая острых респираторных заболеваний у = Му + Ry/x (х - Мx) уравнение регрессии Среднее число острых респираторных заболеваний при температуре -25° = 38, 6 случая (у = 34+2, 3 х (25 -23)=34+4, 6=38, 6 заболевания).
Необходимо определить среднее число острых респираторных заболеваний при температуре 25°. х = -25° Rу/х = 2, 3 заболевания. Мх = -23° Му = 34 случая острых респираторных заболеваний у = Му + Ry/x (х - Мx) уравнение регрессии Среднее число острых респираторных заболеваний при температуре -25° = 38, 6 случая (у = 34+2, 3 х (25 -23)=34+4, 6=38, 6 заболевания).
 Среднеквадратическое отклонение регрессии Необходимо определить, в каких пределах будет варьировать число острых респираторных заболеваний при определенном значении среднемесячной температуры воздуха в случае, если sу – среднеквадратическое отклонение числа острых респираторных заболеваний = 20, 9 ; rху — коэффициент корреляции между числом острых респираторных заболеваний (у) и температурой воздуха в средним за зимний период (х) равен «-0, 7»
Среднеквадратическое отклонение регрессии Необходимо определить, в каких пределах будет варьировать число острых респираторных заболеваний при определенном значении среднемесячной температуры воздуха в случае, если sу – среднеквадратическое отклонение числа острых респираторных заболеваний = 20, 9 ; rху — коэффициент корреляции между числом острых респираторных заболеваний (у) и температурой воздуха в средним за зимний период (х) равен «-0, 7»
 в каких пределах будет варьировать число острых респираторных заболеваний при среднемесячной температуре воздуха -25 ° Среднее число простудных заболеваний при температуре воздуха -25° - 38, 6 Количество простудных заболеваний может колебаться в пределах от 23, 7 заболевания (38, 6 -14, 9=23, 7) до 53, 5 заболевания (38, 6+14, 9=53, 5).
в каких пределах будет варьировать число острых респираторных заболеваний при среднемесячной температуре воздуха -25 ° Среднее число простудных заболеваний при температуре воздуха -25° - 38, 6 Количество простудных заболеваний может колебаться в пределах от 23, 7 заболевания (38, 6 -14, 9=23, 7) до 53, 5 заболевания (38, 6+14, 9=53, 5).
 При температуре -30° (у=38, 6+2, 3 х (3025)=50, 1 заболевания) среднее число простудных заболеваний может колебаться в пределах от 35, 2 заболевания (50, 1 -14, 9=35, 2) до 65, 0 заболевания (50, 1+14, 9=65, 0) т. д.
При температуре -30° (у=38, 6+2, 3 х (3025)=50, 1 заболевания) среднее число простудных заболеваний может колебаться в пределах от 35, 2 заболевания (50, 1 -14, 9=35, 2) до 65, 0 заболевания (50, 1+14, 9=65, 0) т. д.
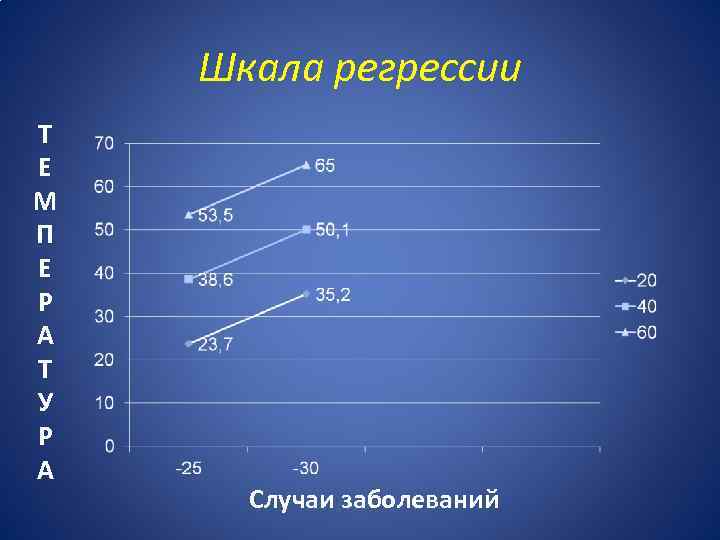 Шкала регрессии Т Е М П Е Р А Т У Р А Случаи заболеваний
Шкала регрессии Т Е М П Е Р А Т У Р А Случаи заболеваний
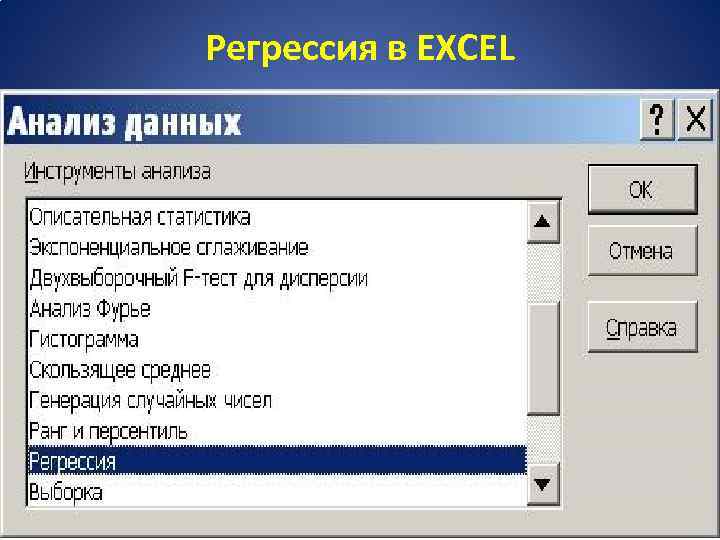 Регрессия в EXCEL
Регрессия в EXCEL
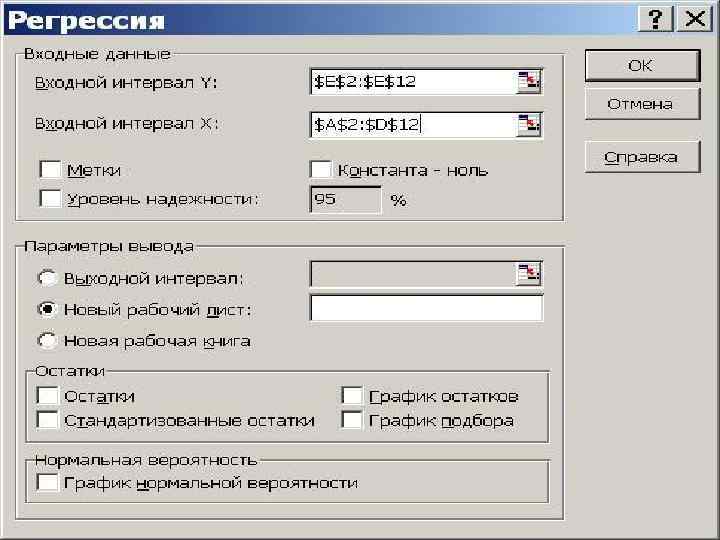
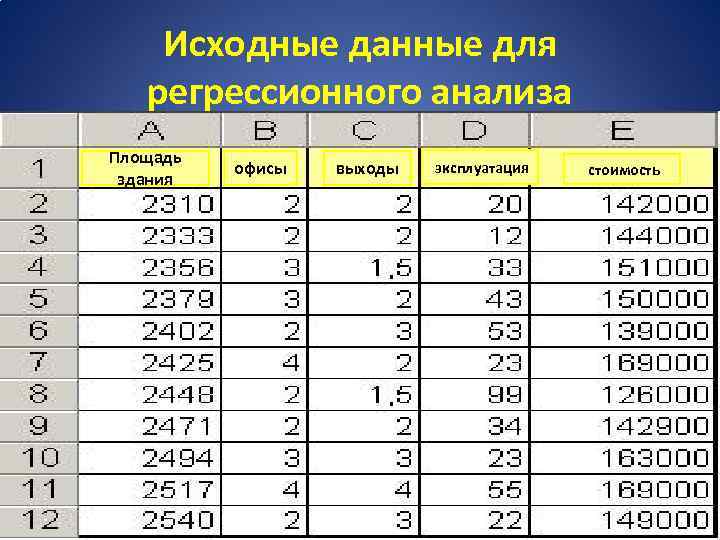 Исходные данные для регрессионного анализа Площадь здания офисы выходы эксплуатация стоимость
Исходные данные для регрессионного анализа Площадь здания офисы выходы эксплуатация стоимость
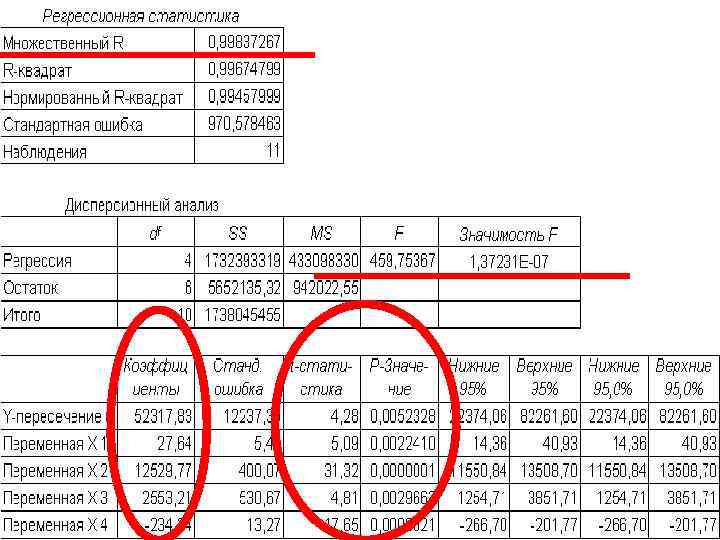
 математическая модель y = 52318 + 27, 64*x 1 + 12530*x 2 + 2553*x 3 - 234, 24*x 4. Если здание имеет площадь 2500 квадратных метров, три офиса, два входа и время эксплуатации - 25 лет, можно оценить его стоимость, используя следующую формулу y = 27, 64*2500 + 12530*3 + 2553*2 - 234, 24*25 + 52318 = 158 261 у. е.
математическая модель y = 52318 + 27, 64*x 1 + 12530*x 2 + 2553*x 3 - 234, 24*x 4. Если здание имеет площадь 2500 квадратных метров, три офиса, два входа и время эксплуатации - 25 лет, можно оценить его стоимость, используя следующую формулу y = 27, 64*2500 + 12530*3 + 2553*2 - 234, 24*25 + 52318 = 158 261 у. е.
 В регрессионном анализе наиболее важными результатами являются • коэффициенты при переменных и Y-пересечение, являющиеся искомыми параметрами модели; • множественный R, характеризующий точность модели для имеющихся исходных данных; • F-критерий Фишера • t-статистика – величины, характеризующие степень значимости отдельных коэффициентов модели.
В регрессионном анализе наиболее важными результатами являются • коэффициенты при переменных и Y-пересечение, являющиеся искомыми параметрами модели; • множественный R, характеризующий точность модели для имеющихся исходных данных; • F-критерий Фишера • t-статистика – величины, характеризующие степень значимости отдельных коэффициентов модели.
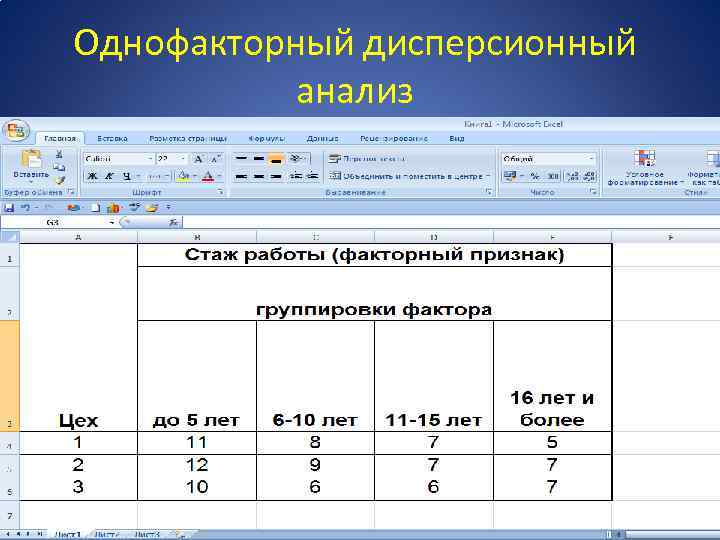 Однофакторный дисперсионный анализ
Однофакторный дисперсионный анализ
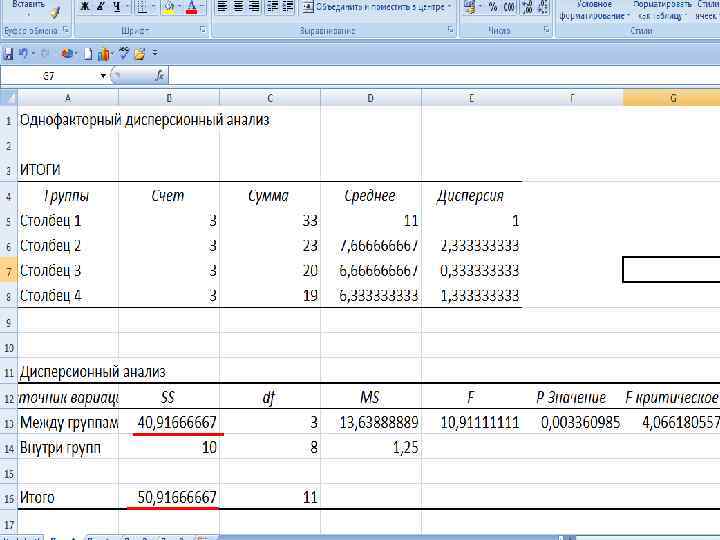
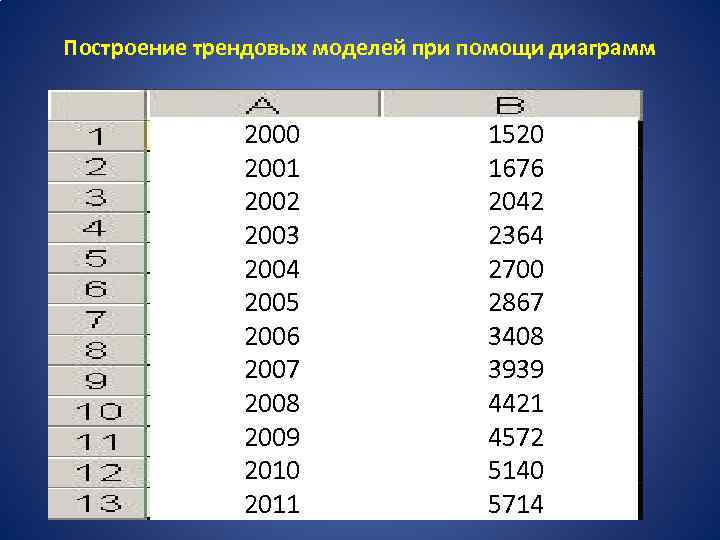 Построение трендовых моделей при помощи диаграмм 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 1520 1676 2042 2364 2700 2867 3408 3939 4421 4572 5140 5714
Построение трендовых моделей при помощи диаграмм 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 1520 1676 2042 2364 2700 2867 3408 3939 4421 4572 5140 5714
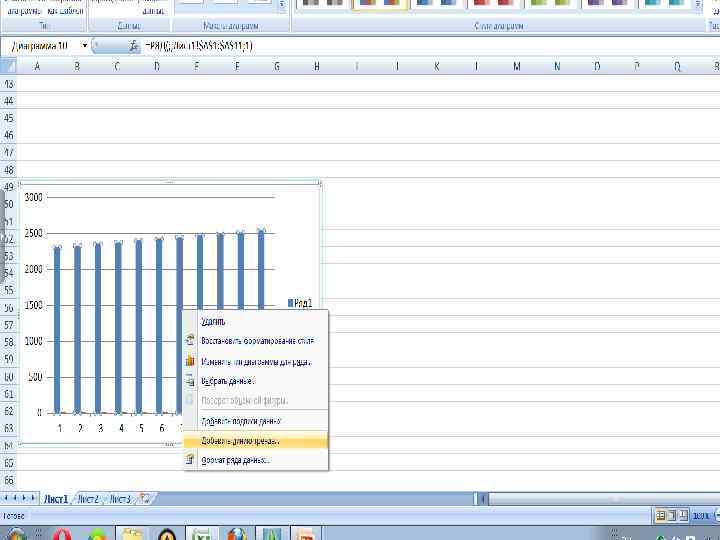
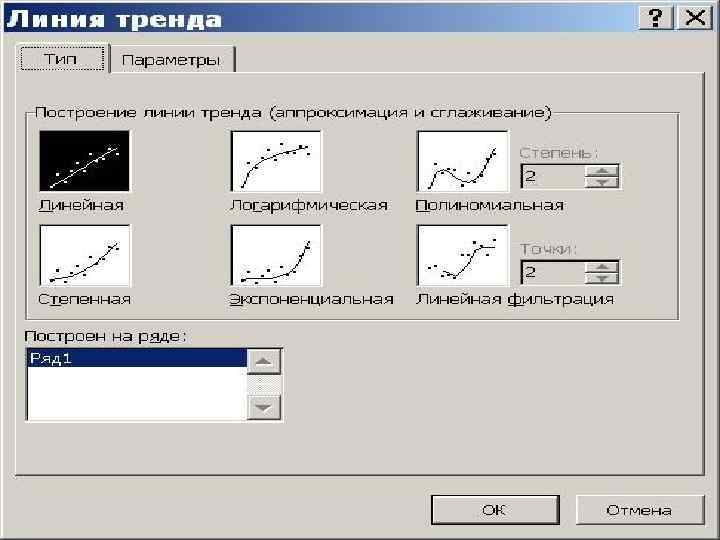
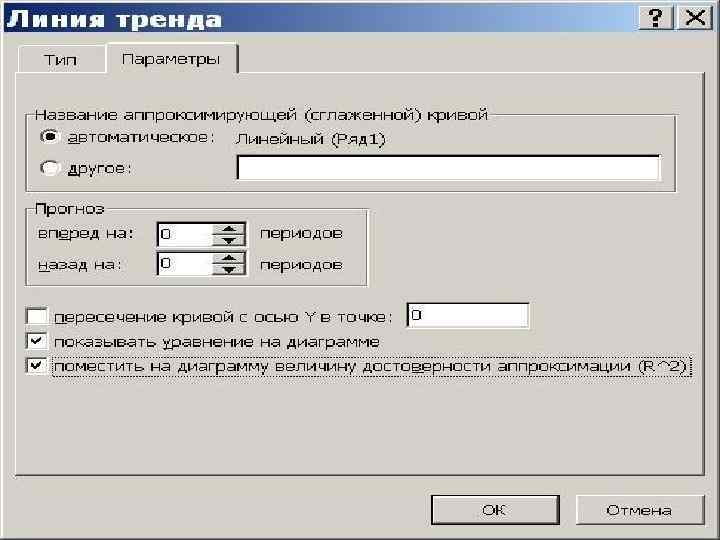
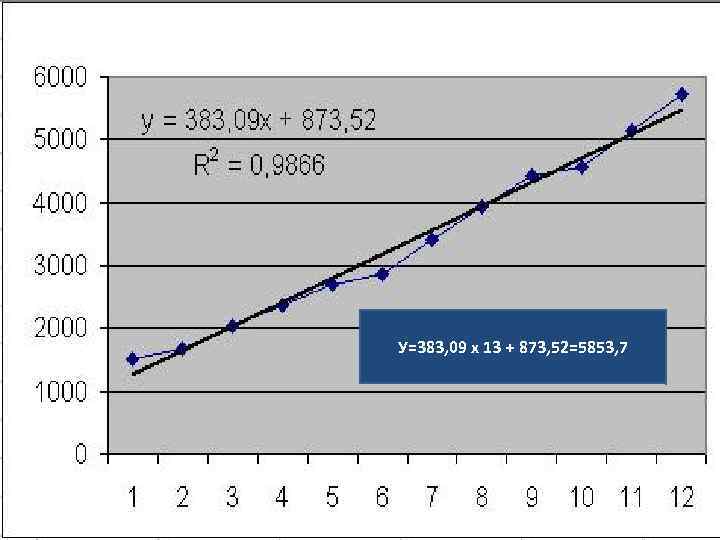 У=383, 09 х 13 + 873, 52=5853, 7
У=383, 09 х 13 + 873, 52=5853, 7
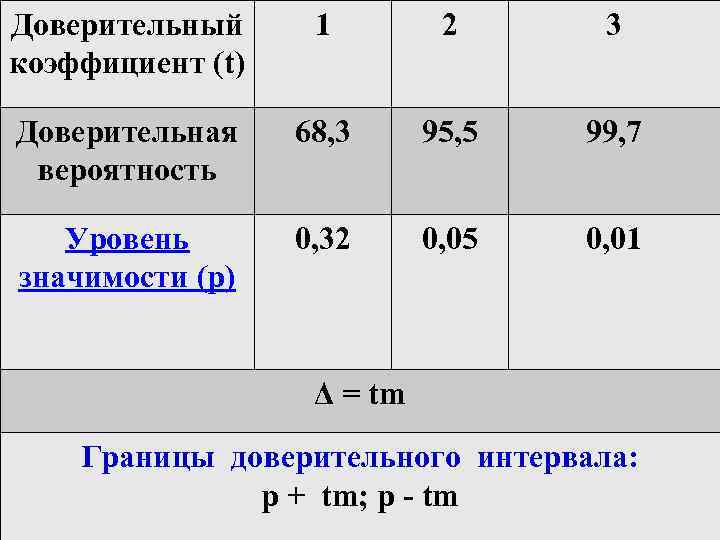 Доверительный коэффициент (t) 1 2 3 Доверительная вероятность 68, 3 95, 5 99, 7 Уровень значимости (р) 0, 32 0, 05 0, 01 Δ = tm Границы доверительного интервала: р + tm; p - tm
Доверительный коэффициент (t) 1 2 3 Доверительная вероятность 68, 3 95, 5 99, 7 Уровень значимости (р) 0, 32 0, 05 0, 01 Δ = tm Границы доверительного интервала: р + tm; p - tm


