s sin t где t R

s = sin t, где t ∊ R

Свойство 2. Функция s = sin t является нечётной. Функция у = f (x), х ∊ Х — нечётная, если f (– x) = – f (x). sin(– t) = – sin t s = sin t — нечётная функция.

1 1 – 1

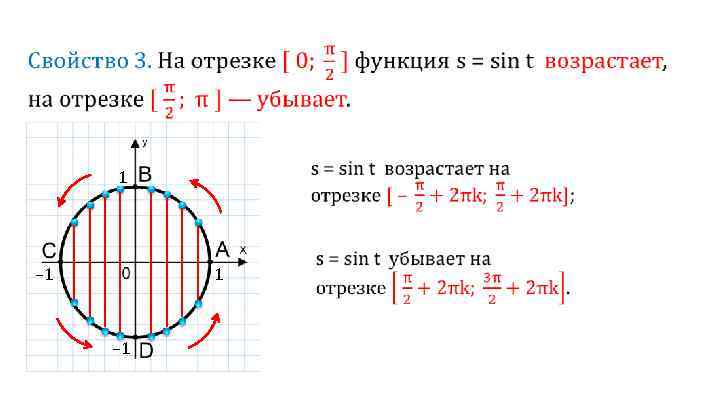
Свойство 4. Функция s = sin t ограничена сверху и снизу. у = f (x) — ограничена снизу, если f (x) ≥ m; у = f (x) — ограничена сверху, если f (x) ≤ М. – 1 ≤ sin t ≤ 1.

s = sin t; sнаим. ; sнаиб. .

у = sin х на отрезке [ 0; π ]. y t 0 cos t 1 0 – 1 0 1 sin t 0 1 0 – 1 0 x 0 y 0 x 0 0

у = sin х на отрезке [ –π; π ]. y 1 x 0 – 1

sin (x + 2π) = sin x. (x + 2π) ∊ [π; 3π ], если х ϵ [–π; π ]. 1 3 – 2 – – 1 2 3

Линию, которая является графиком функции у = sin х, называют синусоидой.

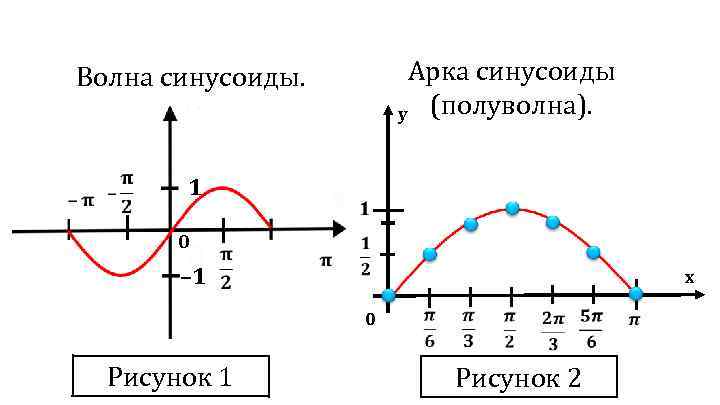Арка синусоиды y (полуволна). Волна синусоиды. 1 0 – 1 x 0 Рисунок 1 Рисунок 2

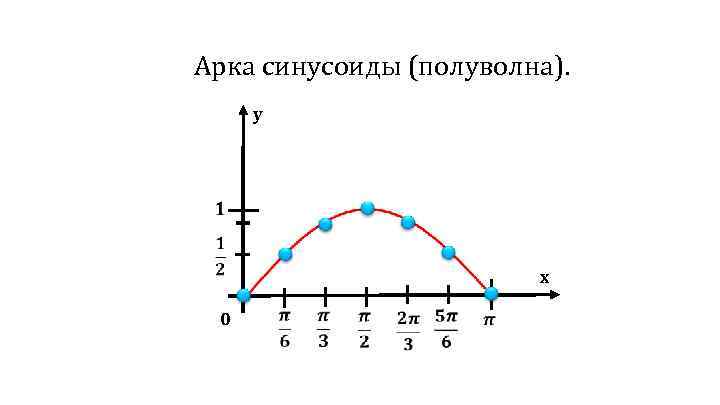Арка синусоиды (полуволна). y x 0

Свойство 6. Функция у = sin х — непрерывная функция.

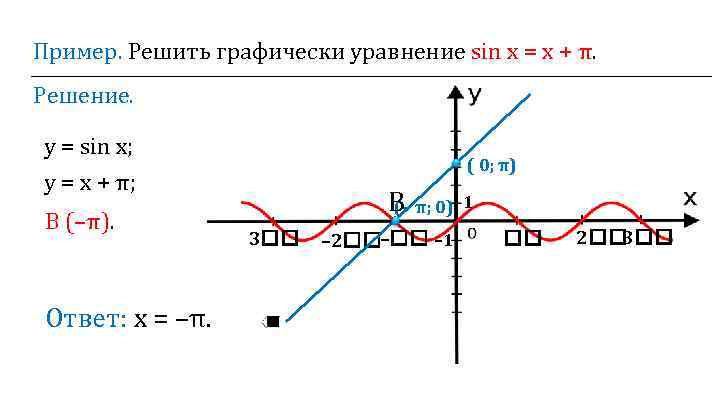Пример. Решить графически уравнение sin х = х + π. Решение. у = sin х; у = х + π; В (–π). Ответ: х = –π. ( 0; π) B π; 0) (– 3 – 2 – – 1 1 2 3