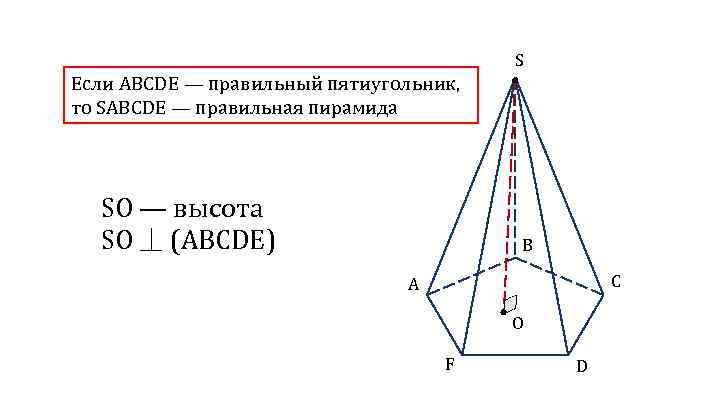
S Если ABCDE — правильный пятиугольник, то SABCDE — правильная пирамида SO — высота SO ⏊ (ABCDE) В С А O F D
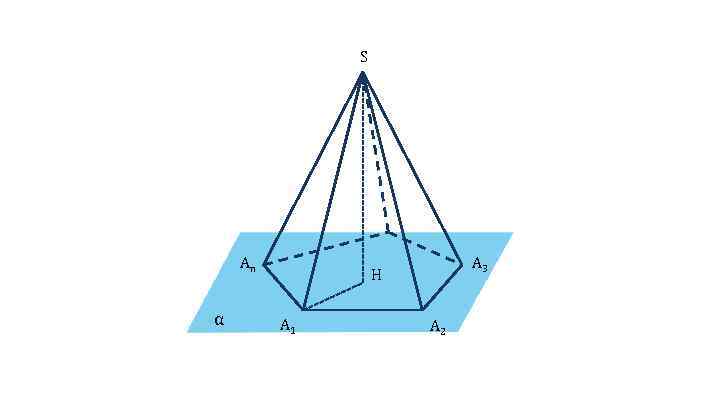
S An α A 3 H A 1 A 2
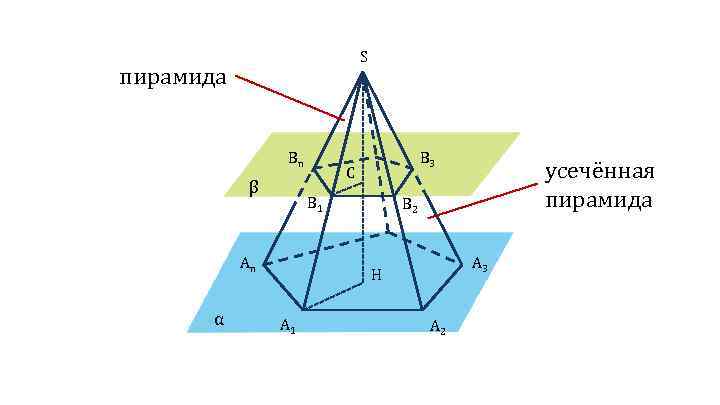
S пирамида Bn β C B 1 An α B 3 B 2 A 3 H A 1 усечённая пирамида A 2
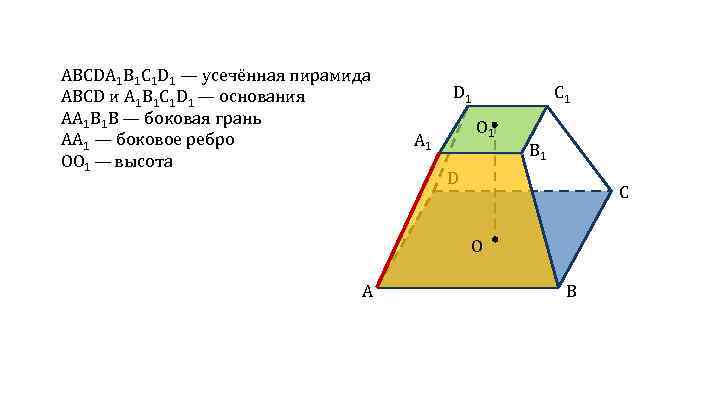
ABCDA 1 B 1 C 1 D 1 — усечённая пирамида ABCD и A 1 B 1 C 1 D 1 — основания АА 1 В 1 В — боковая грань АА 1 — боковое ребро ОО 1 — высота D 1 C 1 O 1 A 1 B 1 D C O A B
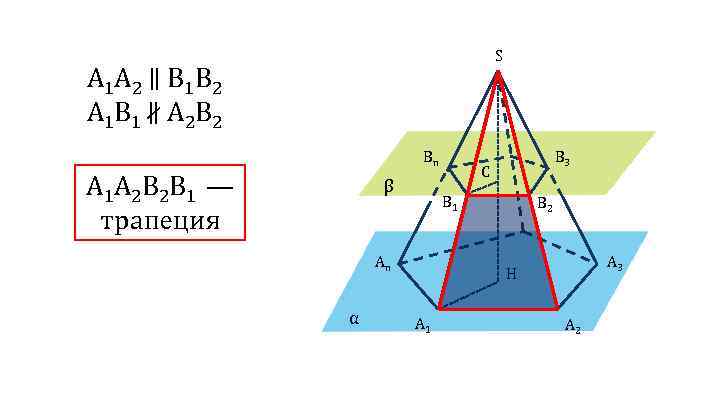
S А 1 А 2 ∥ В 1 В 2 А 1 В 1 ∦ А 2 В 2 Bn А 1 А 2 В 2 В 1 — трапеция β C B 1 An α B 3 B 2 A 3 H A 1 A 2
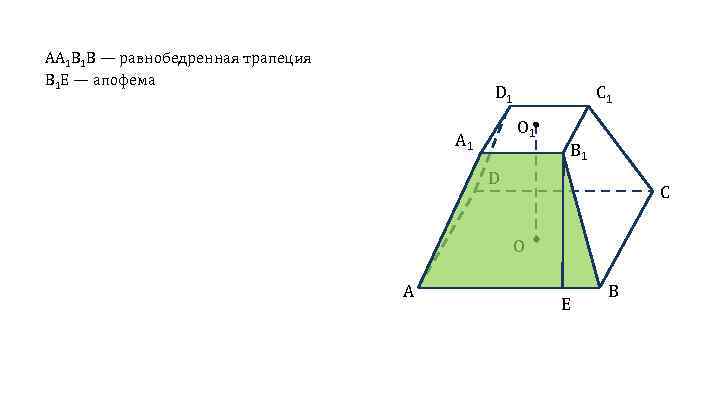
АА 1 В 1 В — равнобедренная трапеция В 1 Е — апофема D 1 C 1 O 1 A 1 B 1 D C O A E B
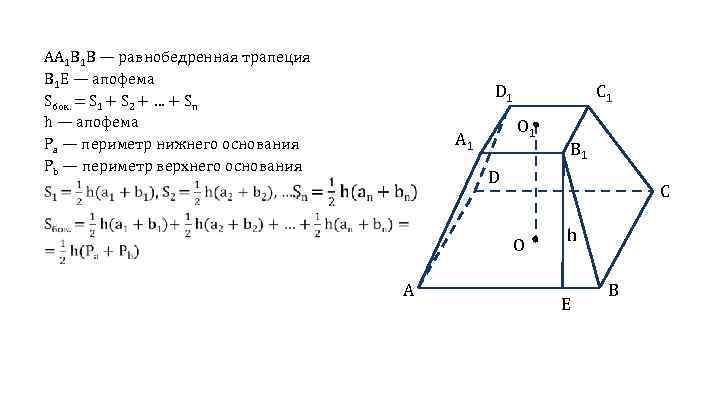
АА 1 В 1 В — равнобедренная трапеция В 1 Е — апофема Sбок. = S 1 + S 2 + … + Sn h — апофема Pa — периметр нижнего основания Pb — периметр верхнего основания D 1 C 1 O 1 A 1 B 1 D C O A h E B
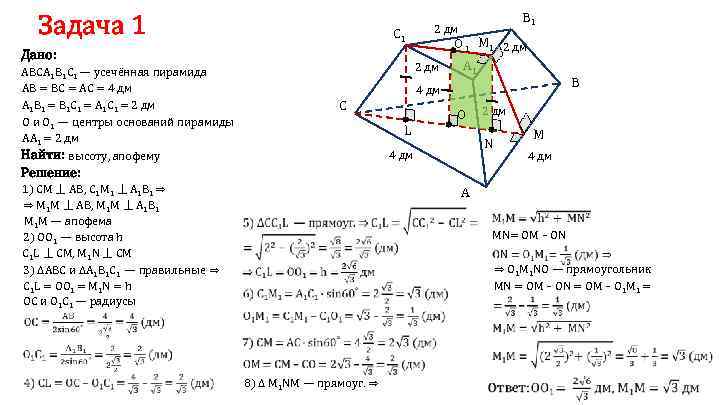
Задача 1 C 1 Дано: 2 дм АВСА 1 В 1 С 1 — усечённая пирамида АВ = ВС = АС = 4 дм А 1 В 1 = В 1 С 1 = А 1 С 1 = 2 дм О и О 1 — центры оснований пирамиды АА 1 = 2 дм Найти: высоту, апофему B 1 2 дм О 1 M 1 2 дм A 1 B 4 дм C О L 2 дм N 4 дм M 4 дм Решение: 1) СМ ⏊ АВ, C 1 М 1 ⏊ А 1 В 1 ⇒ ⇒ М 1 М ⏊ АВ, М 1 М ⏊ А 1 В 1 М 1 М — апофема 2) ОО 1 — высота h С 1 L ⏊ СМ, М 1 N ⏊ СМ 3) ΔАВС и ΔА 1 В 1 С 1 — правильные ⇒ С 1 L = ОО 1 = М 1 N = h ОС и О 1 С 1 — радиусы A ⇒ О 1 М 1 NО — прямоугольник MN = ОМ – О 1 М 1 = 8) Δ M 1 NM — прямоуг. ⇒ MN= ОМ – ОN
Скачать презентацию S Если ABCDE правильный пятиугольник то SABCDE
31. Усеченная пирамида.ppt