С 44 -54 С 20 -28

С. 44 -54

С. 20 -28

С. 5 -15

Предыдущая лекция • Латинские прямоугольники и квадраты.

• Проще всего получать латинские прямоугольники циклическим сдвигом строк.

• Название «латинский квадрат» берёт начало от Леонарда Эйлера, который использовал латинские буквы вместо цифр в таблице.

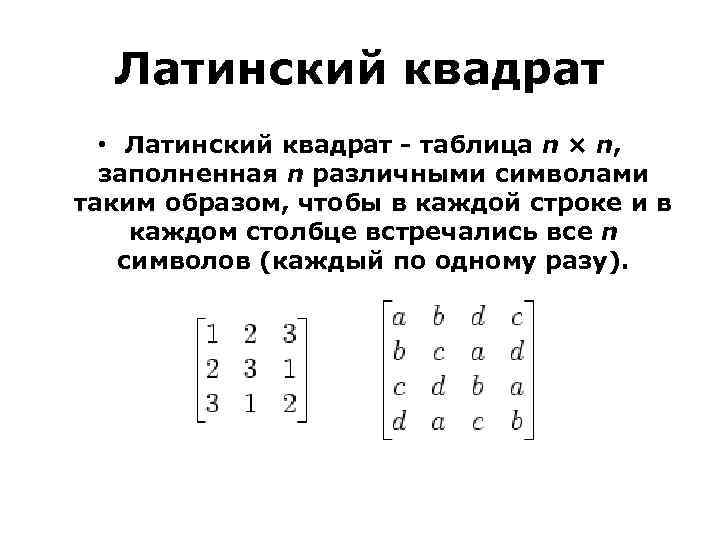Латинский квадрат • Латинский квадрат - таблица n × n, заполненная n различными символами таким образом, чтобы в каждой строке и в каждом столбце встречались все n символов (каждый по одному разу).

Греко-латинский квадрат ab cd b c ad cd ab d a cb αβγδ γδαβ δγβα βαδγ

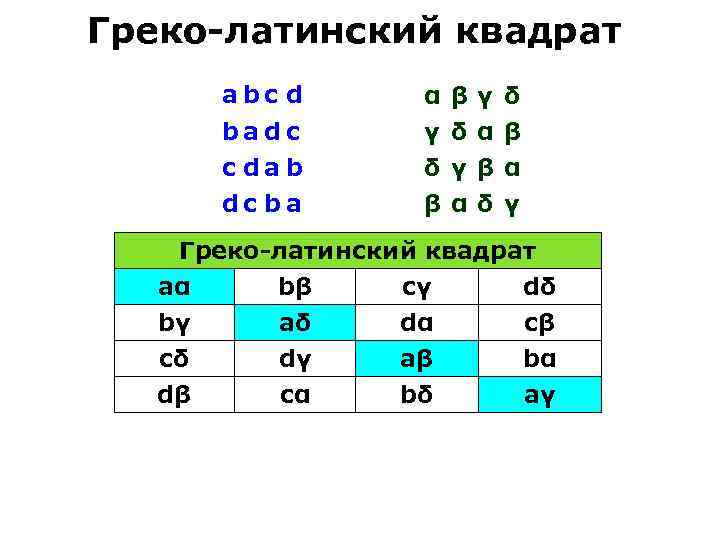Греко-латинский квадрат abc d badc c dab dc ba α γ δ β β δ γ α β δ δ β α γ Греко-латинский квадрат aα bβ cγ dδ bγ aδ dα cβ cδ dγ aβ bα dβ cα bδ aγ

• Судоку (яп. 数独 ) — головоломка. • В переводе с японского «су» — «цифра» , «доку» — «стоящая отдельно» . • Иногда судоку называют «магическим квадратом» , что не верно, так как судоку является латинским квадратом 9 -го порядка.

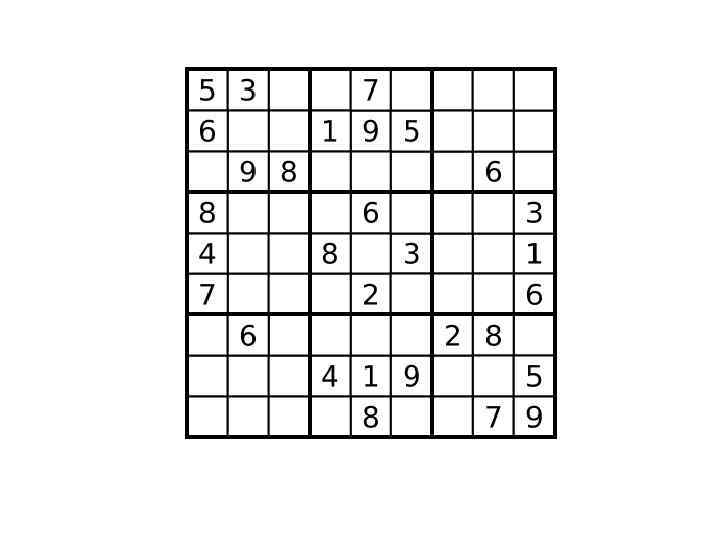
• Количество возможных комбинаций в судоку 9 x 9 составляет по расчётам 6 670 903 752 021 072 936 960.

Магический квадрат

• На известной гравюре Альбрехта Дюрера «Меланхолия» (1514 г. – почти полтысячи лет назад ):

• Маги ческий, или волше бный квадра т — это квадратная таблица , заполненная n n числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. • Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. • Нормальным называется магический квадрат, заполненный целыми числами от 1 до n n.

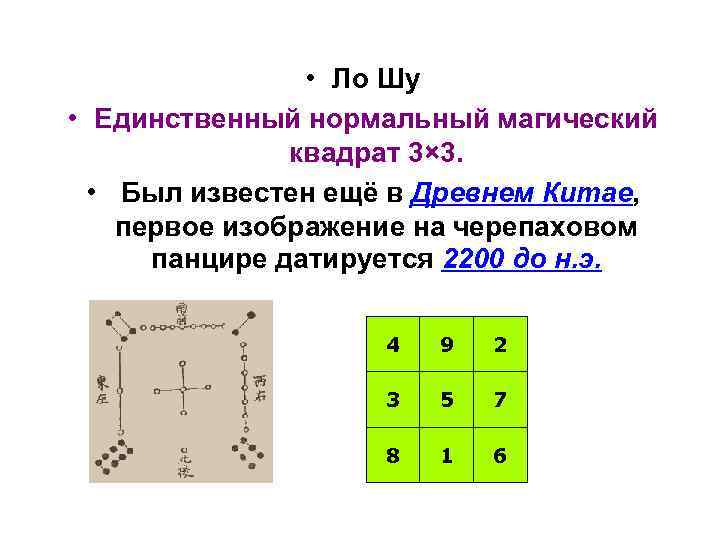• Ло Шу • Единственный нормальный магический квадрат 3× 3. • Был известен ещё в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 до н. э. 4 9 2 3 5 7 8 1 6

• Сумма чисел в каждой строке, столбце и на диагоналях, называется магической константой, M. Магическая константа нормального волшебного квадрата зависит только от n и определяется формулой

• Магический квадрат послужил предвестником нового направления в комбинаторике – оно рассматривает так называемые блок схемы – таблицы из систем чисел или множеств, которые удовлетворяют сразу большому количеству очень жёстких ограничений. Настолько жёстких, что речь идёт уже не о перечислении возможных вариантов, а о самом существовании такой схемы.

Конечные проективные плоскости

• Проективная плоскость — это множества точек и прямых и такое отношение инцидентности, что • - для любых двух различных точек существует единственная инцидентная им прямая; • - для любых двух различных прямых существует единственная инцидентная им точка — точка пересечения; • - существуют такие четыре точки, что прямая, инцидентная двум из них, не инцидентна ни одной из двух других.

Плоскость Фано • Плоскость Фано имеет 7 точек и 7 прямых. • Отношение инцидентности на плоскости Фано задано следующей таблицей: 1 1 0 1 0 0 0 1 1 1 0 0 0 0 1 1 0 1 0 0 1 1 0 0

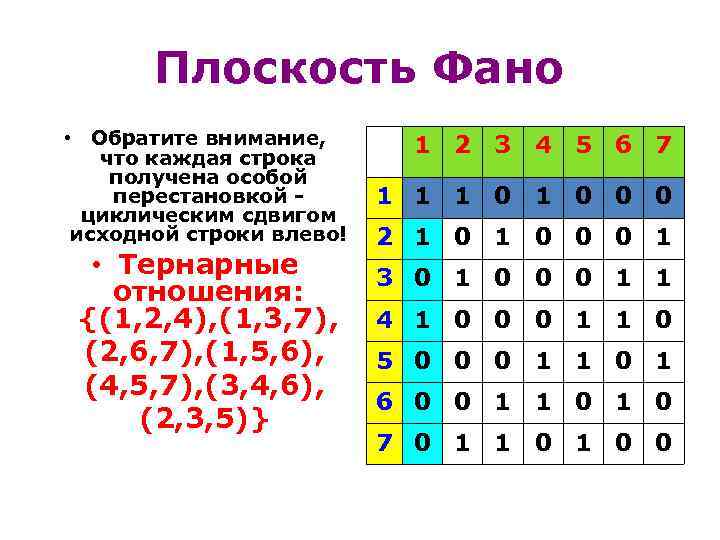Плоскость Фано • Обратите внимание, что каждая строка получена особой перестановкой - циклическим сдвигом исходной строки влево! • Тернарные отношения: {(1, 2, 4), (1, 3, 7), (2, 6, 7), (1, 5, 6), (4, 5, 7), (3, 4, 6), (2, 3, 5)} 1 2 3 4 5 6 7 1 1 1 0 0 0 2 1 0 0 0 1 3 0 1 0 0 0 1 1 4 1 0 0 0 1 1 0 5 0 0 0 1 1 0 1 6 0 0 1 1 0 7 0 1 1 0 0

Плоскость Фано в виде тернарных отношений

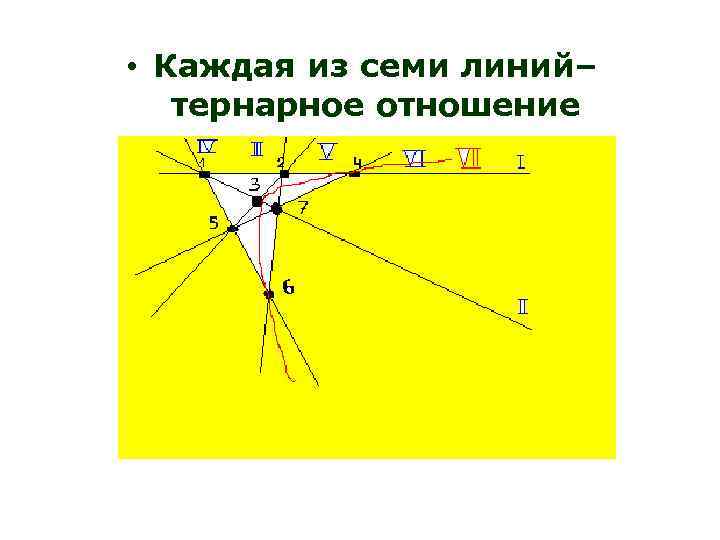• Каждая из семи линий– тернарное отношение

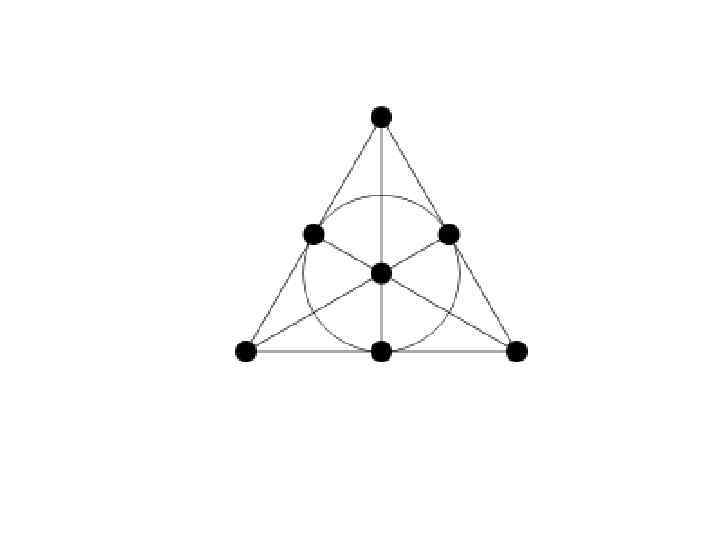
Палиндром: SATOR AREPO TENET OPERA ROTAS (лат. Сеятель Арепо с трудом держит колеса)

Лекция 10 • Метод рекуррентных соотношений.

Метод рекуррентных соотношений состоит в том, что решение комбинаторной задачи с n предметами выражается через решение аналогичной задачи с меньшим числом предметов с помощью некоторого соотношения, которое называется рекуррентным. Пользуясь этим соотношением, искомую величину можно вычислить алгоритмически, исходя из того, что для небольшого количества предметов решение задачи легко находится.

• Рекуррентным называют соотношение, в котором для вычисления некоторого члена числовой последовательности используют значения предыдущих членов.

Чи сла Фибона ччи — элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 …

Решение рекуррентных соотношений • Пусть Тогда

Разделим обе части выражения на получим

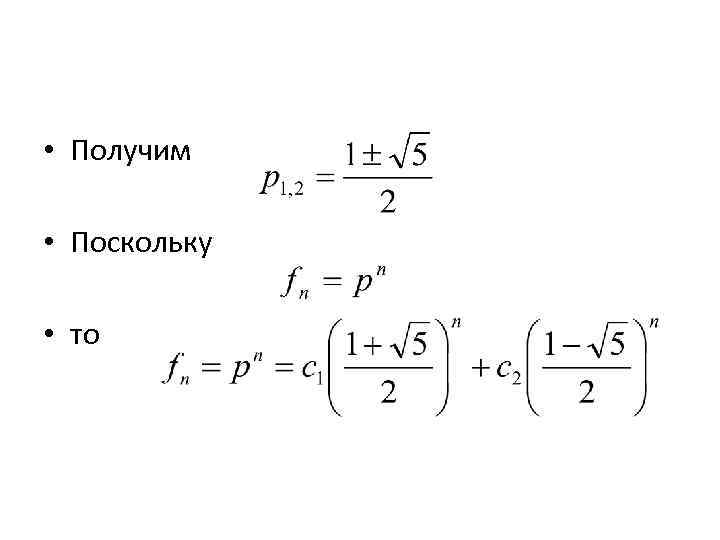• Получим • Поскольку • то

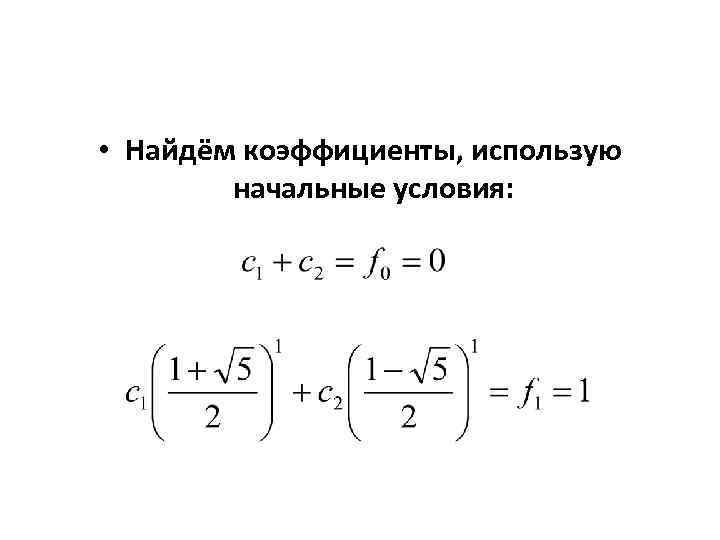• Найдём коэффициенты, использую начальные условия:

• Таким образом:

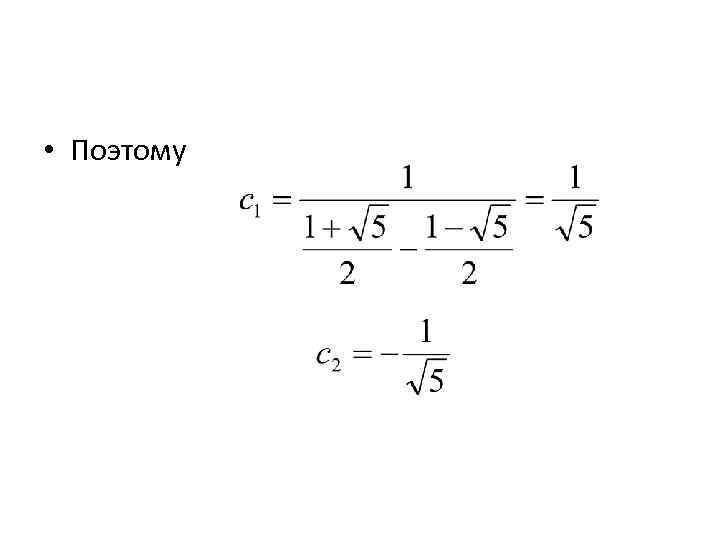• Поэтому

• Посему • Это формула Бине • Где «золотое сечение»

Решение рекуррентных соотношений • В общем случае линейное рекуррентное соотношение с постоянными коэффициентами имеет вид

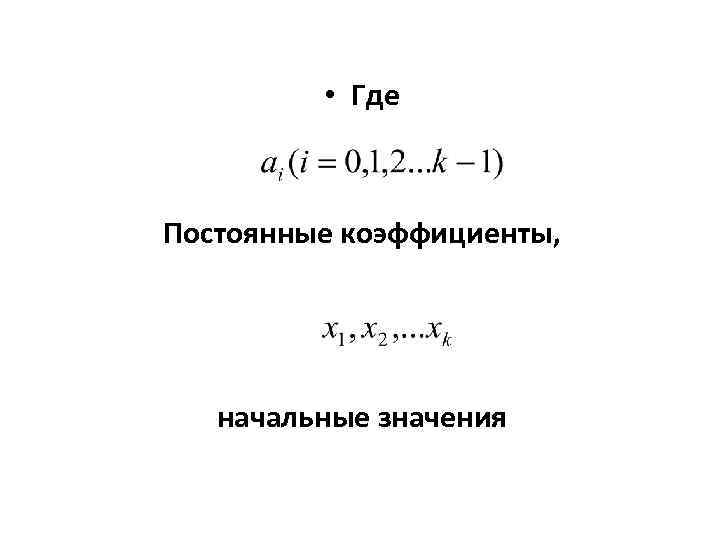• Где Постоянные коэффициенты, начальные значения

• Решение находим в виде • Подставляя в исходное выражение получаем полином k-ой степени (после деления на

• Это уравнение имеет k корней • Тогда общее решение имеет вид • Где неизвестные коэффициенты находят по начальным условиям, составляя соответствующую систему линейных уравнений

СКМ для комбинаторных вычислений

• В информатике вычисления на конечных математических структурах часто называют комбинаторными вычислениями, и они требуют комбинаторного анализа для установления свойств и оценки применимости используемых алгоритмов • Комбинаторные задачи могут быть решены, например, системой компьютерной математики Matematica (3, 4) фирмы Wolfram Research, Inc. – пакет расширения «Дискретная математика» (Discrete. Math) – комбинаторика и ее функции (Combinatorica, Combinatorial. Functions)

• В справочнике пакета Mathematica 5. 1 закладка The Mathematica book, в ней – Advanced Mathematics, далее – Mathematics Functions, Combinatorial Functions:

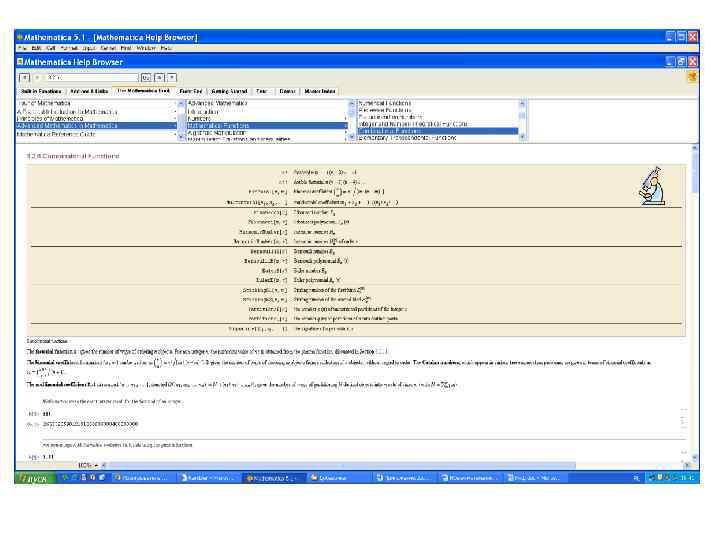
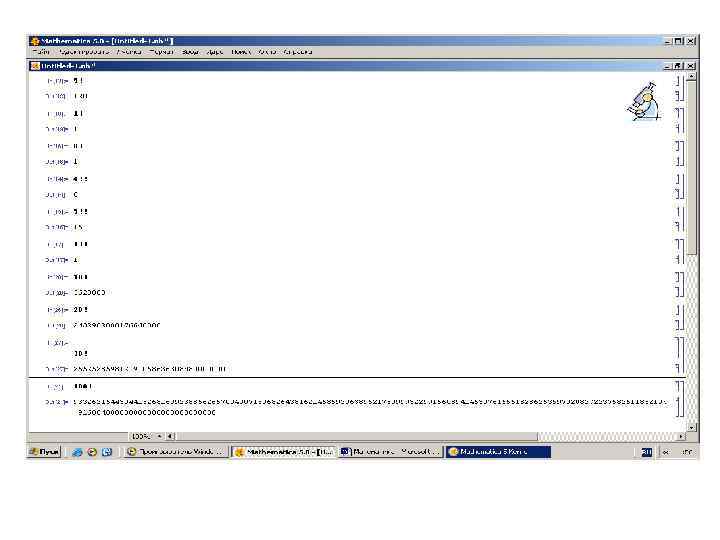
• • • • • • In[13]: = 5 ! Out[13]= 120 In[19]: = 1 ! Out[19]= 1 In[16]: = 0 ! Out[16]= 1 In[14]: = 4 !! Out[14]= 8 In[15]: = 5 !! Out[15]=15 In[17]: = 1!! Out[17]= 1 In[20]: = 10 ! Out[20]= 3628800 In[26]: = 20 ! Out[26]= 2432902008176640000 In[27]: = 30 ! Out[27]= 2652528598121910586363308480000000 -------------------------------In[21]: = 100 ! Out[21]= 93326215443944152681692238856266700490715968264381621468592963 89521759999322991560894146397615651828625369792082722375825118 5210916864000000000000

• Обратим внимание на факториал числа 100 – это 158 разрядное число!

• Как проводить вычисления? • Выделяем пример выполнения требуемой функции и копируем в новый открытый файл результатов, редактируем, а затем инициируем вычисления, нажав клавишу Shift с клавишей Enter.

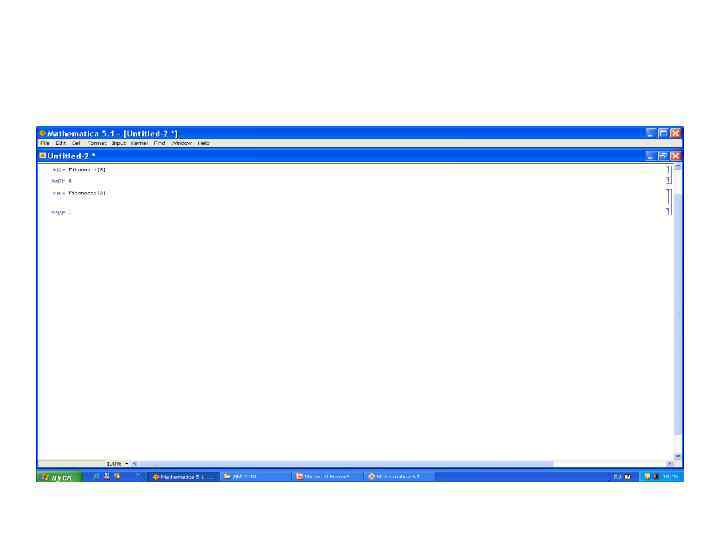
• Вычисление числа сочетаний без повторений выполняется с использованием функции биномиальных коэффициентов Binomial[n, m]. • Причём, можно получить выражение только с одним из числовых значений: • Binomial[n, 2], здесь задано только m:

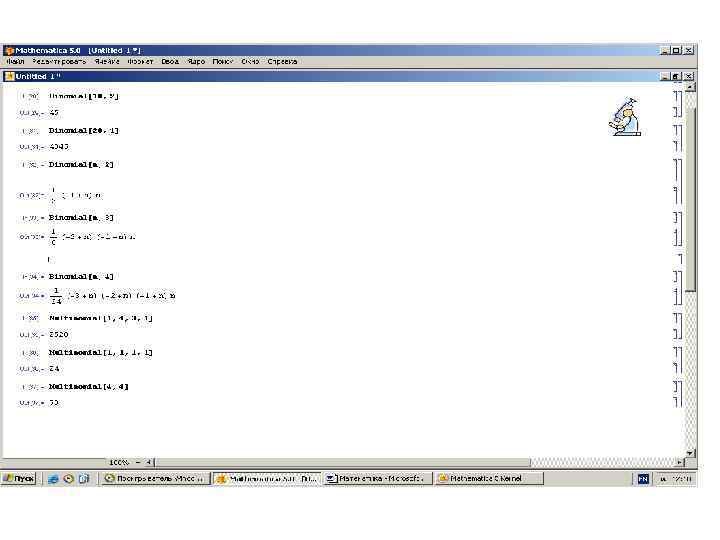
In[29]: = Binomial[10, 2] Out[29]= 45 In[31]: = Binomial[20, 4] Out[31]= 4845 In[32]: = Binomial[n, 2] Out[32]= 1 (-1+n)n 2 In[33]: = Binomial[n, 3] Out[33]= 1 (-2+n)(-1+n)n 3 In[34]: = Binomial[n, 4] Out[34]= 1 (-3+n)(-2+n)(-1+n)n 24 In[35]: = Multinomial[1, 4, 3, 1] Out[35]= 2520 In[36]: = Multinomial[1, 1, 1, 1] Out[36]= 24 In[37]: = Multinomial[4, 4] Out[37]= 70

• Перестановки с повторениями, например, функция: Multinomial[1, 4, 3, 1]. • Здесь[1, 4, 3, 1] – векторсостав

• Discrete. Math`Combinatorica` расширяет пакет Mathematica более 450 функциями комбинаторики (Сombinatorics) и теории графов (Graph theory). • Пакет расширения находится на вкладке Add ons & Links, затем выбирается закладка Combinatorica.

• Перечисление всех перестановок – как без повторений, так и с повторениями – в зависимости от заданного в квадратных скобках вектора, каждый символ, даже повторяющийся, программа считает уникальным – функция Minimum. Change. Permutations[{1, 2, 3}].

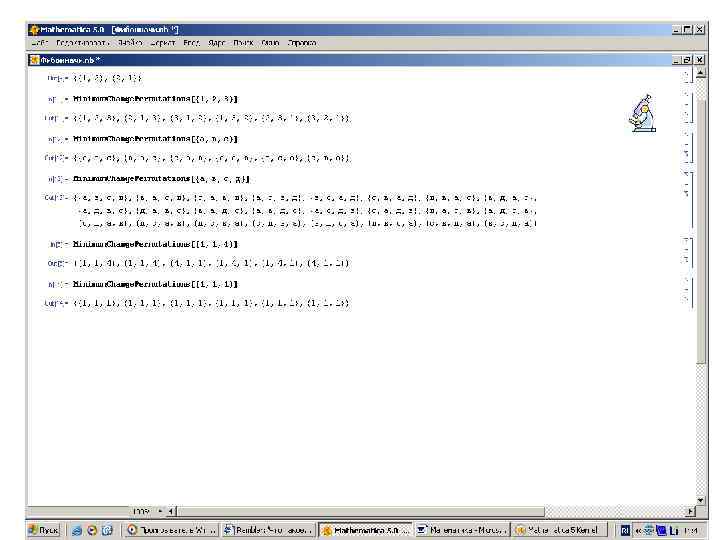
Out[9]= {{1, 2}, {2, 1}} In[10]: = Minimum. Change. Permutations[{1, 2, 3}] Out[10]= {{1, 2, 3}, {2, 1, 3}, {3, 1, 2}, {1, 3, 2}, {2, 3, 1}, {3, 2, 1}} In[12]: = Minimum. Change. Permutations[{a, в, c}] Out[12]= {{а, в, с}, {в, а, с}, {с, а, в}, {а, с, в}, {в, с, а}, {с, в, а}} In[13]: = Minimum. Change. Permutations[{a, в, c, д}] Out[13]= {{а, в, с, д}, {в, а, с, д}, {с, а, в, д}, {а, с, в, д}, {в, с, а, д}, {с, в, а, д}, {д, в, а, с}, {в, д, а, с}, {а, д, в, с}, {д, а, в, с}, {в, а, д, с}, {а, в, д, с}, {а, с, д, в}, {с, а, д, в}, {д, а, с, в}, {а, д, с, в}, {с, д, а, в}, {д, с, в, а}, {с, д, в, а}, {в, д, с, а}, {д, в, с, а}, {с, в, д, а}, {в, с, д, а}} In[6]: = Minimum. Change. Permutations[{1, 1, 4}] Out[6]= {{1, 1, 4}, {4, 1, 1}, {1, 4, 1}, {4, 1, 1}} In[14]: = Minimum. Change. Permutations[{1, 1, 1}] Out[14]= {{1, 1, 1}, {1, 1, 1}, {1, 1, 1}}

• Формирование подмножеств (Subsets). • Например: • а) формирование цикла из одноэлементных подмножеств функция To. Cycles[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}]. • Получаем: {{1}, {2}, {3}, {4}, {5}, {6}, {7}, { 8}, {9}, {10}};

• б) формирование подмножеств в соответствие с кодом Грея – функция Gray. Code. Subsets[{1, 2, 3, 4}] формирует последовательность подмножеств, отличающихся от соседних только одним элементом (соседние наборы): • {{}, {4}, {3, 4}, {3}, {2, 3, 4}, {2, 4 }, {2}, {1, 2, 4}, {1, 2, 3}, {1, 3, 4}, {1}}. • Здесь {} – пустое множество;

• с) формирование k-элементных подмножеств, например, 3 -х элементных из множества {1, 2, 3, 4, 5}, функция KSubsets[{1, 2, 3, 4, 5}, 3]: • {{1, 2, 3}, {1, 2, 4}, {1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, { 2, 4, 5}, {3, 4, 5}}.

Разбиения и композиции • а) разбиение по заданному числу. • Функция Partitions[6]: • {{6}, {5, 1}, {4, 2}, {4, 1, 1}, {3, 3}, {3, 2, 1}, {3, 1, 1, 1}, {2, 2, 2}, {2, 2, 1, 1}, {2, 1, 1}, {1, 1, 1, 1}};

• б) определение мощности множества разбиений по заданному числу (длина разбиения). • Функция Length[Partitions[20]]: • 627;

• в) множество разбиений. • Функция Set. Partitions[3]: • {{{1, 2, 3}}, {{1}, {2, 3}}, {{1, 2}, {3}}, {{1, 3}, {2}}, {{1}, {2}, {3}}} – получили различные разбиения трёхэлементного множества.

Композиции. • По существу, это перечисление сочетаний с повторениями – всех возможных векторов-составов. • Функция Compositions[5, 3]: • {{0, 0, 5}, {0, 1, 4}, {0, 2, 3}, {0, 3, 2}, {0, 4, 1}, {0, 5, 0}, {1, 0, 4}, {1, 1, 3}, {1, 2, 2}, {1, 3, 1}, {1, 4, 0}, {2, 0, 3}, {2, 1, 2}, {2, 2, 1}, {2, 3, 0}, {3, 0, 2}, {3, 1, 1}, {3, 2, 0}, { 4, 0, 1}, {4, 1, 0}, {5, 0, 0}} – это, очевидно, множество сочетаний из пяти по три.

Применение греко-латинских квадратов в теории планирования экспериментов • Если есть система, на которую действуют 4 различных параметра (например воздействие N различных веществ на бактерии N различных групп), которые могут принимать по N значений нужно рассмотреть греко-латинский квадрат порядка N. • Таким образом можно провести N·N экспериментов, вместо N·N·N·N (в случае полного перебора вариантов)

• Предположим, что нужно провести несколько экспериментов, зависящих от 3 параметров 1≤a, b, c≤n, так чтобы для каждой пары параметров были опробованы все n² вариантов. • Тогда нужно взять любой латинский квадрат порядка n и провести n² экспериментов с параметрами a = номер строки, b = номер столбца, c = значение в клетке латинского квадрата.

• Леона рдо Пиза нский (лат. Leonardo Pisano, Пиза, около 1170 — около 1250) — первый крупный математик средневековой Европы. • Более известен под прозвищем Фибона ччи (Fibonacci), что в переводе с итальянского означает «хороший сын родился» (Figlio Buono Nato Ci). • Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. • Позже посетил Египет, Сирию, Византию, Сицилию. Леонардо изучал труды математиков стран ислама (таких как ал-Хорезми и Абу Камил); по арабским переводам он ознакомился также с достижениями античных и индийских математиков. • На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки.

Чжунго — самоназвание Китая