Скачать презентацию С 4 2012 ü Включены планиметрические геометрические Скачать презентацию С 4 2012 ü Включены планиметрические геометрические

С4 часть I.ppt

  • Количество слайдов: 22

С 4 2012 С 4 2012

ü Включены планиметрические геометрические задачи, содержащие в условии некоторую неопределенность, которая позволяет трактовать условие ü Включены планиметрические геометрические задачи, содержащие в условии некоторую неопределенность, которая позволяет трактовать условие неоднозначно. ü В результате удается построить несколько чертежей, удовлетворяющих условию задачи. ü Такие задачи называют многовариантными задачами. ü Перебор вариантов является частью решения задач такого типа.

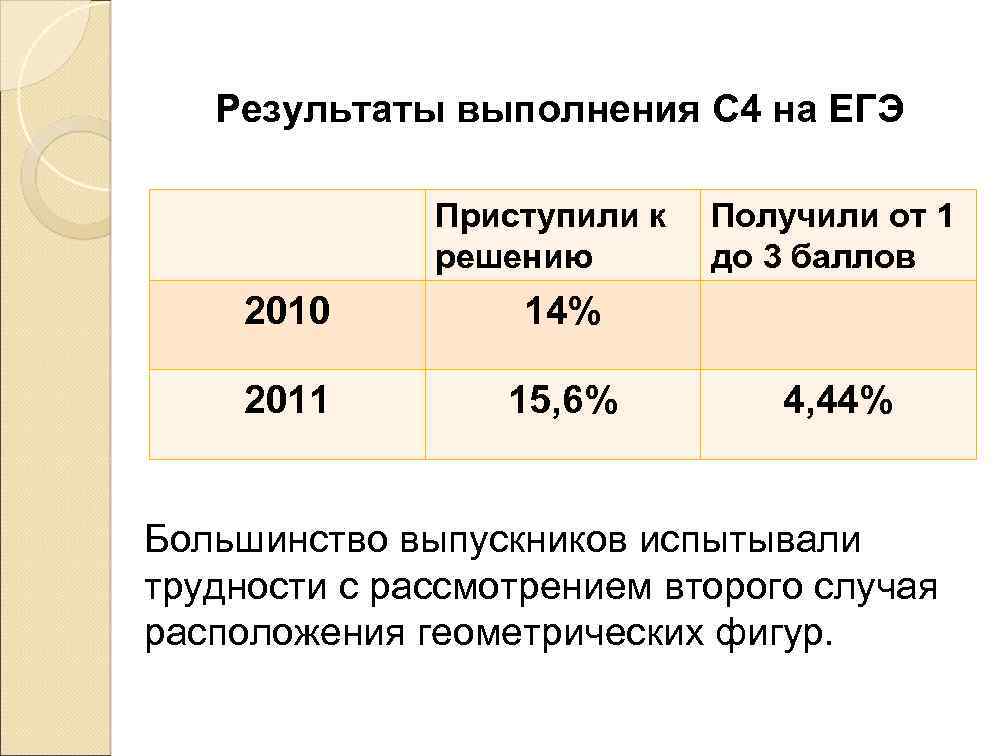Результаты выполнения С 4 на ЕГЭ Приступили к решению 2010 14% 2011 15, 6% Результаты выполнения С 4 на ЕГЭ Приступили к решению 2010 14% 2011 15, 6% Получили от 1 до 3 баллов 4, 44% Большинство выпускников испытывали трудности с рассмотрением второго случая расположения геометрических фигур.

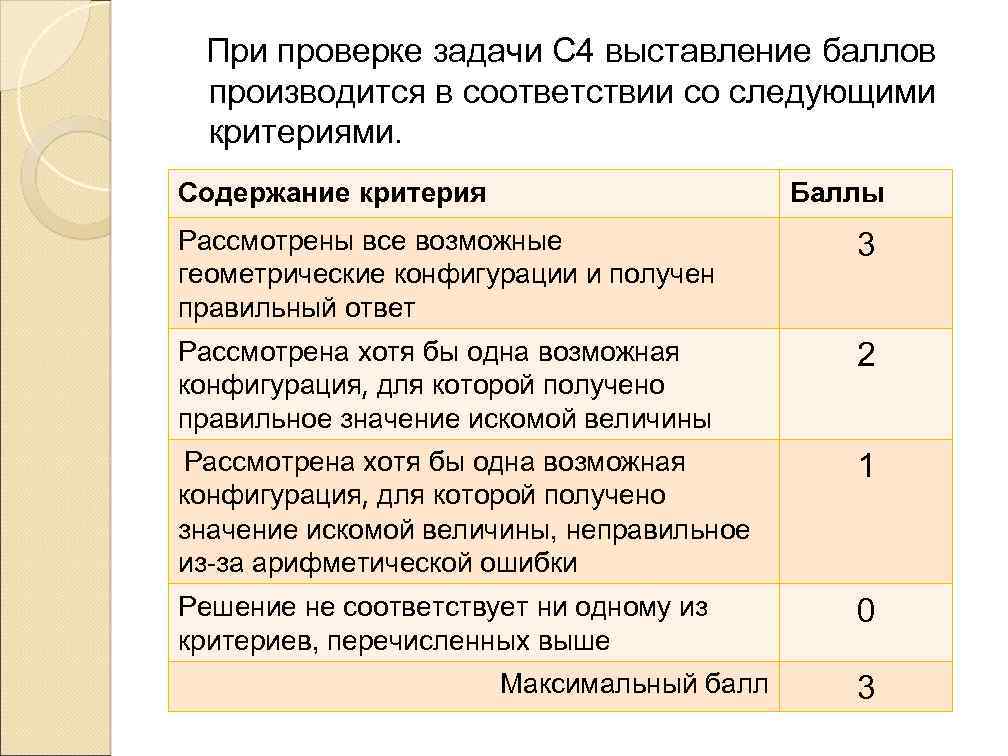При проверке задачи С 4 выставление баллов производится в соответствии со следующими критериями. Содержание При проверке задачи С 4 выставление баллов производится в соответствии со следующими критериями. Содержание критерия Баллы Рассмотрены все возможные геометрические конфигурации и получен правильный ответ 3 Рассмотрена хотя бы одна возможная конфигурация, для которой получено правильное значение искомой величины 2 Рассмотрена хотя бы одна возможная конфигурация, для которой получено значение искомой величины, неправильное из-за арифметической ошибки 1 Решение не соответствует ни одному из критериев, перечисленных выше 0 Максимальный балл 3

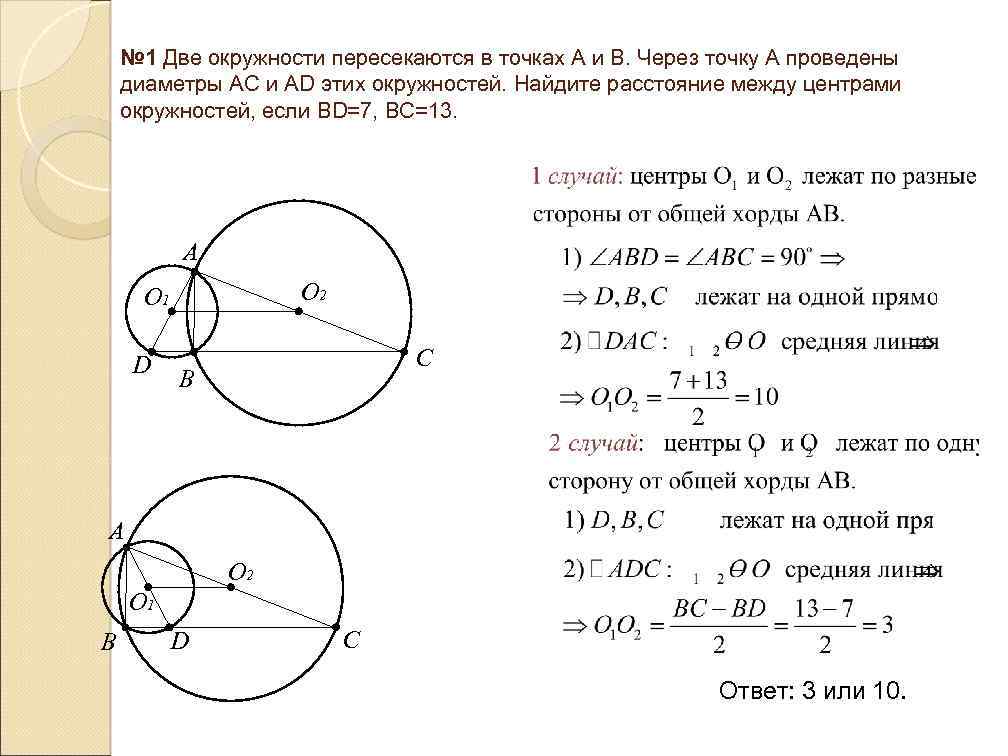№ 1 Две окружности пересекаются в точках А и В. Через точку А проведены № 1 Две окружности пересекаются в точках А и В. Через точку А проведены диаметры АС и АD этих окружностей. Найдите расстояние между центрами окружностей, если ВD=7, ВС=13. A O 2 O 1 D C B A O 2 O 1 B D C Ответ: 3 или 10.

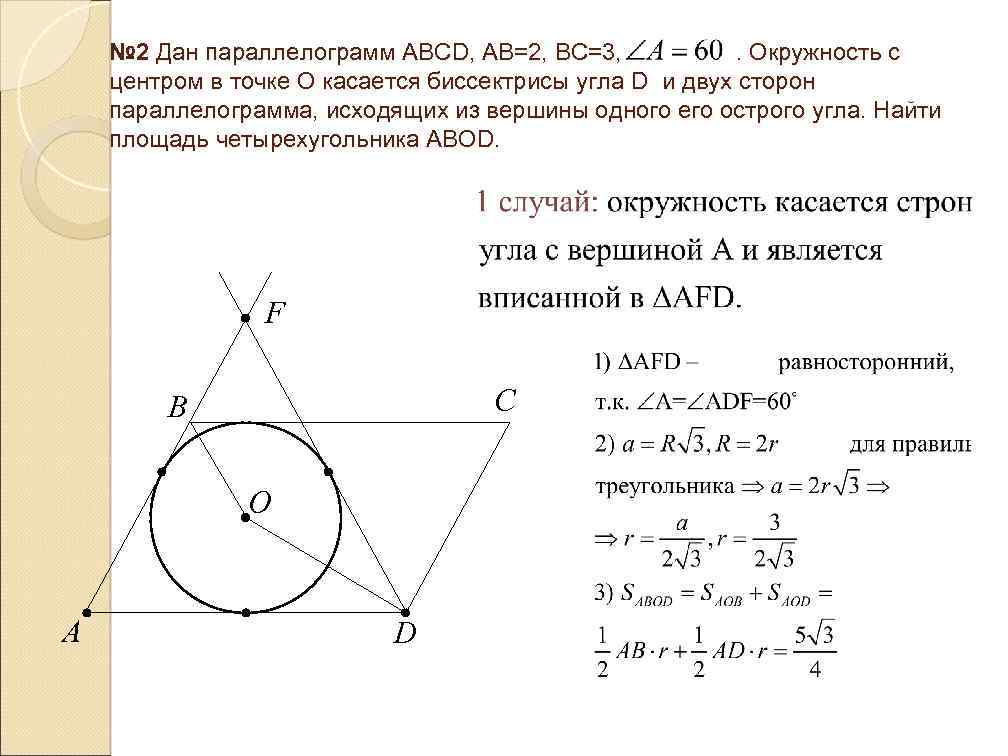№ 2 Дан параллелограмм ABCD, AB=2, BC=3, . Окружность с центром в точке О № 2 Дан параллелограмм ABCD, AB=2, BC=3, . Окружность с центром в точке О касается биссектрисы угла D и двух сторон параллелограмма, исходящих из вершины одного его острого угла. Найти площадь четырехугольника АВОD. F C B O A D

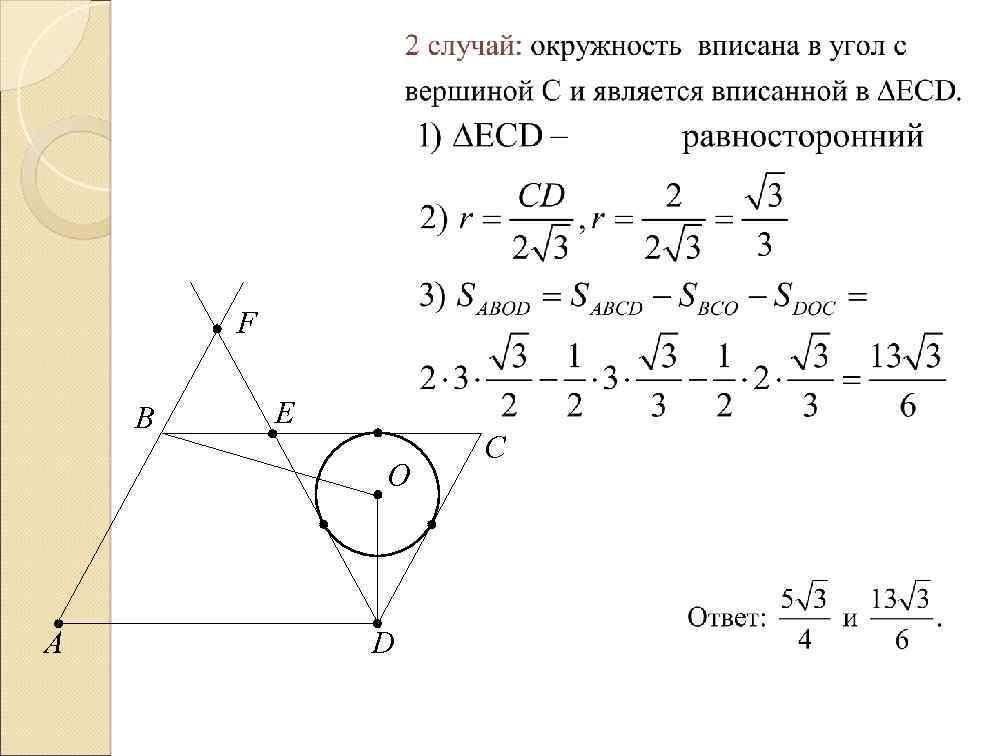F B E O A D C F B E O A D C

ЕГЭ 2011 Периметр равнобедренной трапеции равен 136. Известно, что в эту трапецию можно вписать ЕГЭ 2011 Периметр равнобедренной трапеции равен 136. Известно, что в эту трапецию можно вписать окружность, причем боковая сторона делится точкой касания в отношении 9: 25. Прямая, проходящая через центр окружности и вершину трапеции, отсекает от трапеции треугольник. Найти отношение площади этого треугольника к площади трапеции. B L C M O A N P D

B C E Q O A H D B C E Q O A H D

Трен. раб. 2011 Расстояние между параллельными прямыми равно 12. На одной из них лежит Трен. раб. 2011 Расстояние между параллельными прямыми равно 12. На одной из них лежит точка С, а на другой – точки А и В, причем треугольник АВС – остроугольный и равнобедренный и его боковая сторона равна 13. Найдите радиус окружности, вписанной в треугольник АВС. C 13 13 12 O B H A

C 13 12 O B H 13 A C 13 12 O B H 13 A

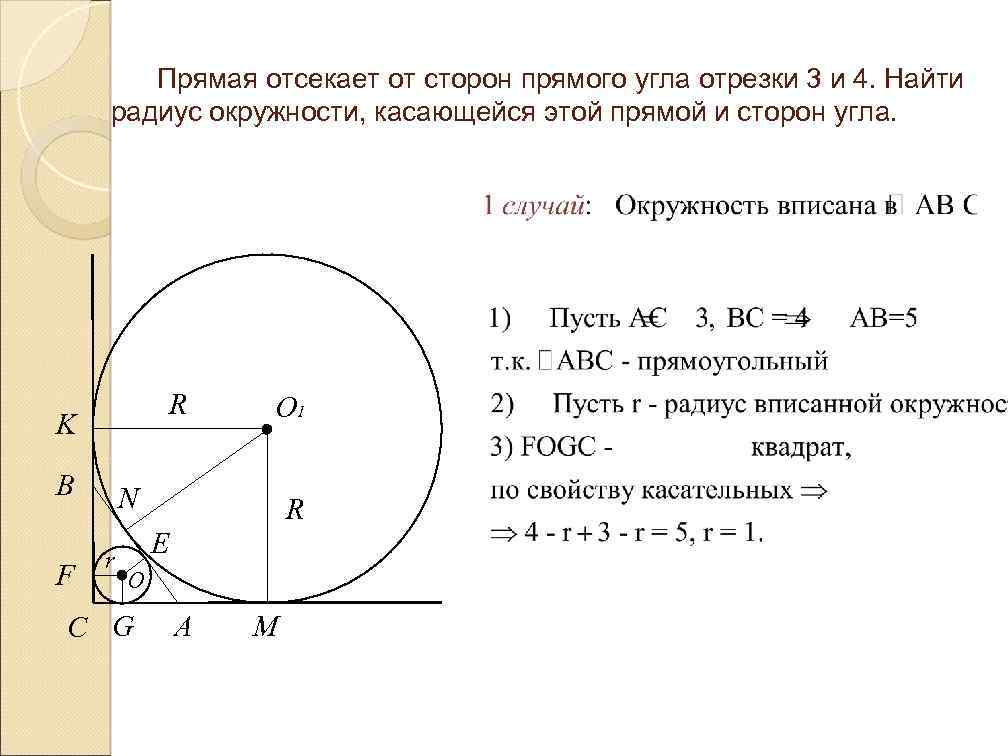Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найти радиус окружности, касающейся Прямая отсекает от сторон прямого угла отрезки 3 и 4. Найти радиус окружности, касающейся этой прямой и сторон угла. R K B F O 1 N r R E O C G A M

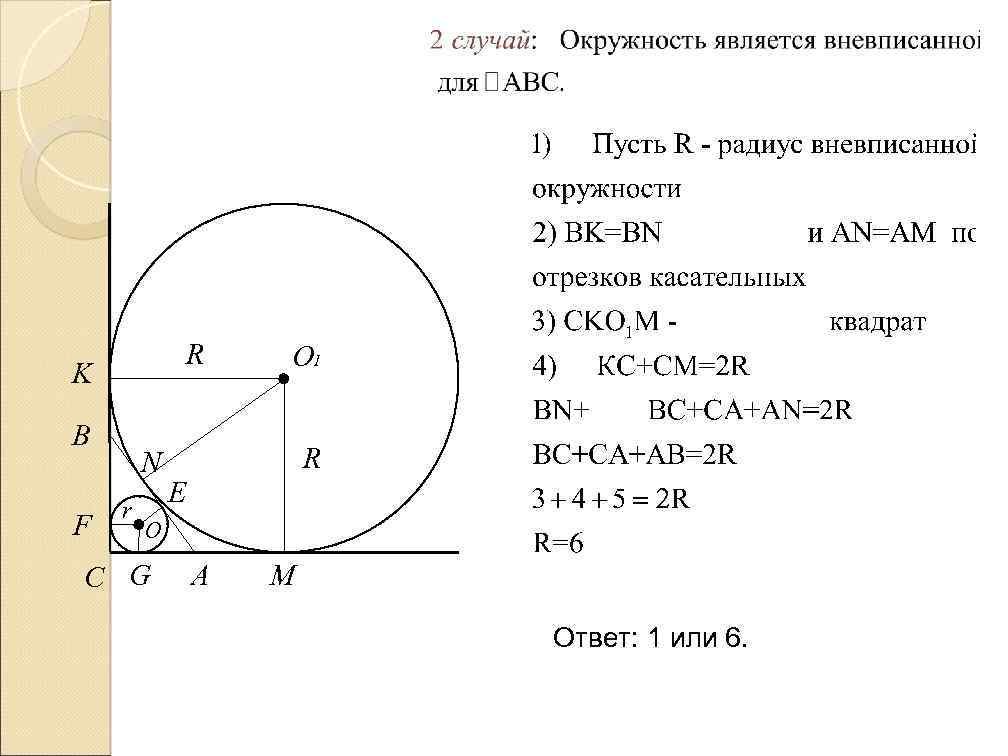R K B F N r O 1 R E O C G A R K B F N r O 1 R E O C G A M Ответ: 1 или 6.

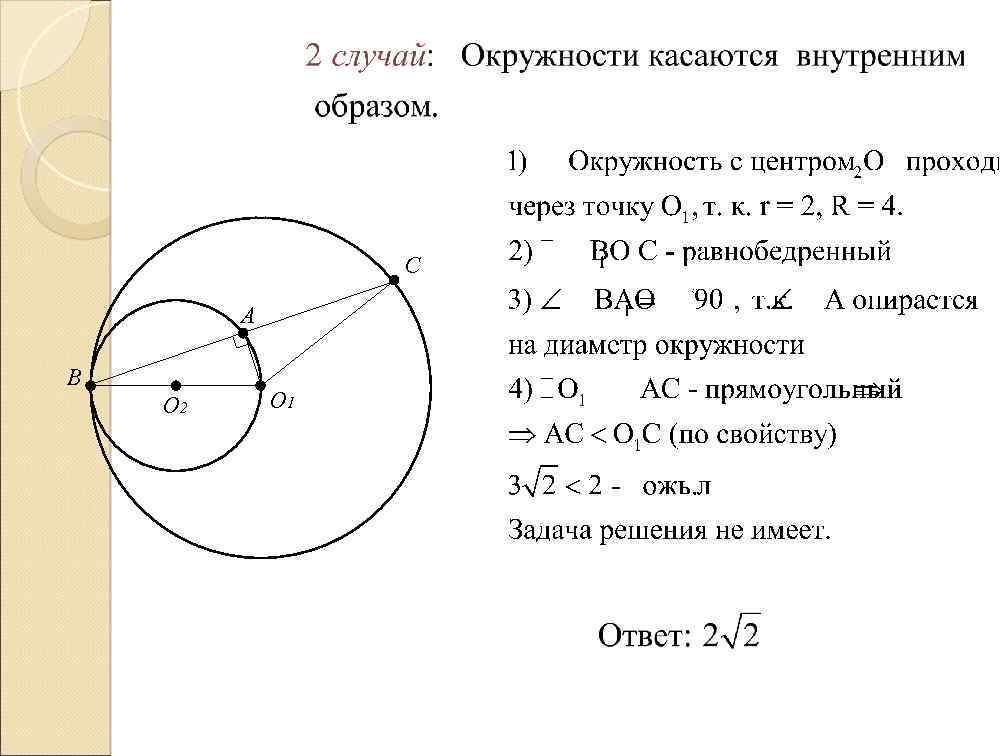
ЕГЭ 2010. Окружности радиусов 2 и 4 касаются в точке В. Через точку В ЕГЭ 2010. Окружности радиусов 2 и 4 касаются в точке В. Через точку В проведена прямая, пересекающая второй раз меньшую окружность в точке А, а большую – в точке С. Известно, что АС =. Найти ВС. C K O 2 B A K 1 O 1

C A B O 2 O 1 C A B O 2 O 1

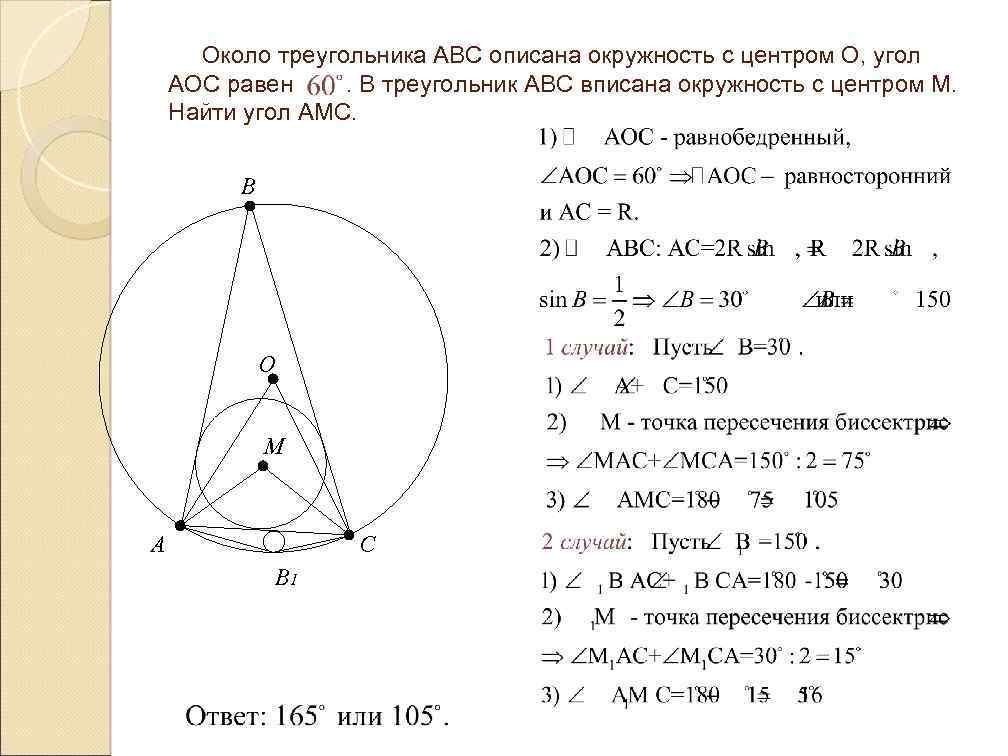Около треугольника АВС описана окружность с центром О, угол АОС равен. В треугольник АВС Около треугольника АВС описана окружность с центром О, угол АОС равен. В треугольник АВС вписана окружность с центром М. Найти угол АМС. B O M A C B 1

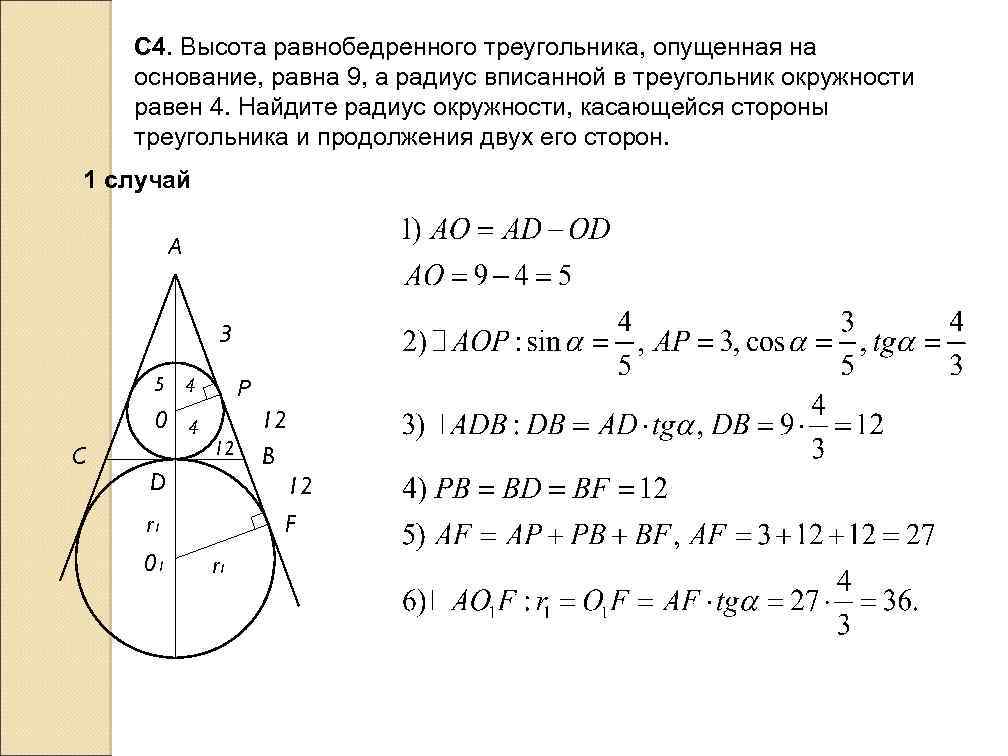С 4. Высота равнобедренного треугольника, опущенная на основание, равна 9, а радиус вписанной в С 4. Высота равнобедренного треугольника, опущенная на основание, равна 9, а радиус вписанной в треугольник окружности равен 4. Найдите радиус окружности, касающейся стороны треугольника и продолжения двух его сторон. 1 случай А 3 Р 5 4 ёё 0 4 C 12 D 12 F r 1 01 12 B r 1

С 4. Высота равнобедренного треугольника, опущенная на основание, равна 9, а радиус вписанной в С 4. Высота равнобедренного треугольника, опущенная на основание, равна 9, а радиус вписанной в треугольник окружности равен 4. Найдите радиус окружности, касающейся стороны треугольника и продолжения двух его сторон. 2 случай K А 02 r 2 0 C D B Q

Решу ЕГЭ. В прямоугольнике АВСD со сторонами АВ=4 и ВС=10 на стороне АD расположены Решу ЕГЭ. В прямоугольнике АВСD со сторонами АВ=4 и ВС=10 на стороне АD расположены точки М и N таким образом, что DM=4, при этом Р- точка пересечения прямых BN и CM. Площадь треугольника MNP равна 1. Найдите длину отрезка, соединяющего точки M и N. 10 B C 4 x K A N α y β M P D

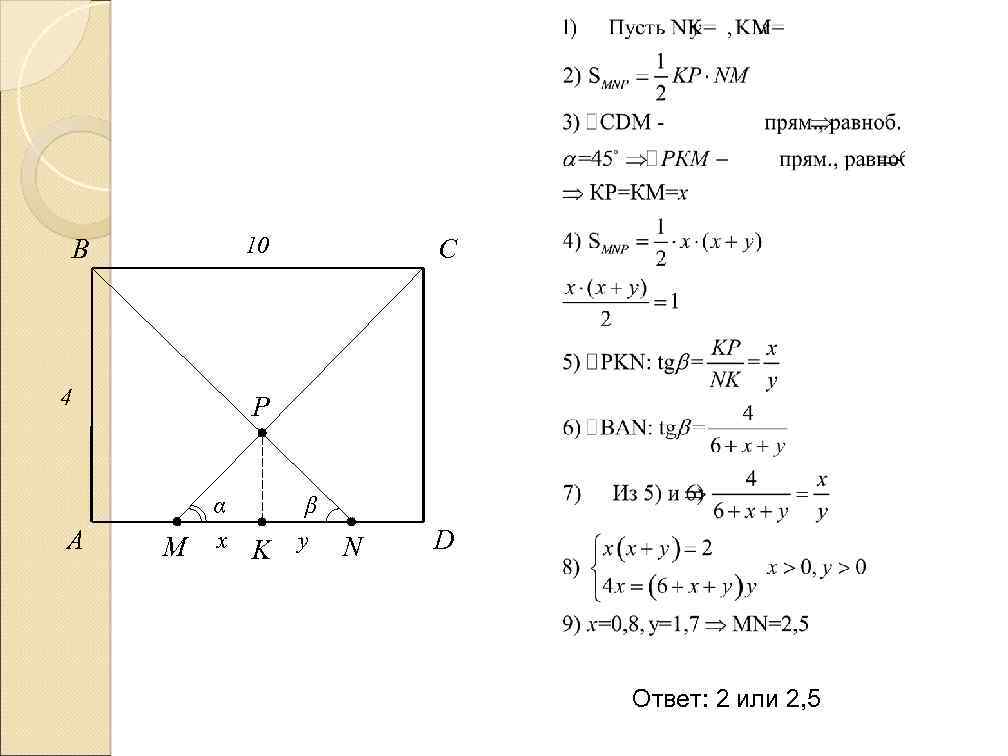10 B 4 A C P M α x K β y N D 10 B 4 A C P M α x K β y N D Ответ: 2 или 2, 5

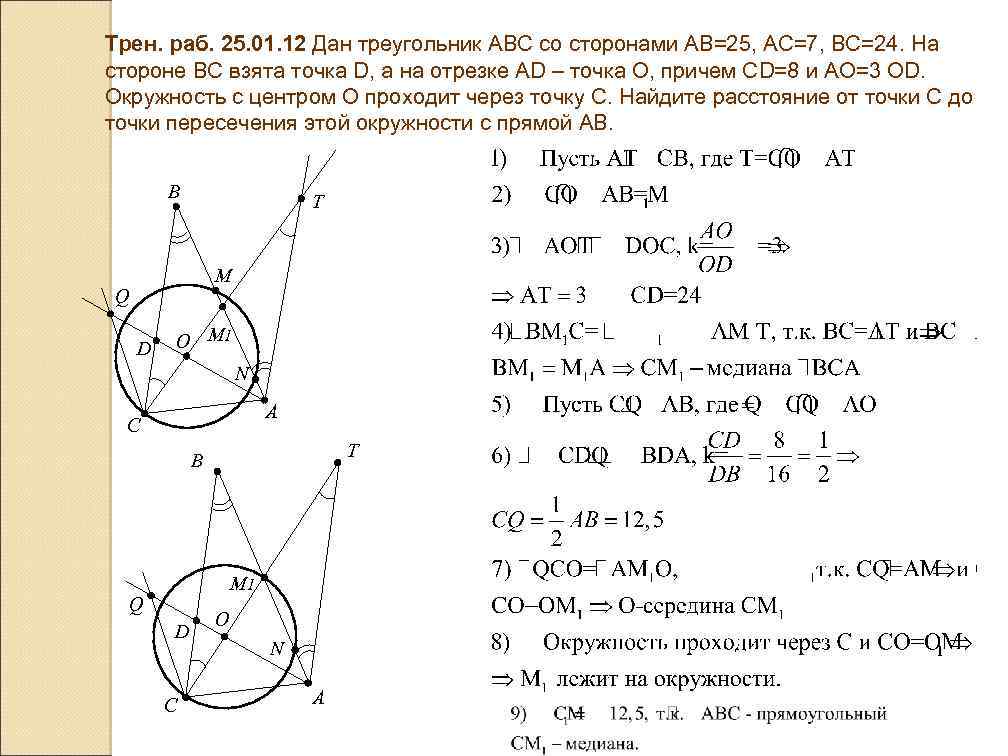Трен. раб. 25. 01. 12 Дан треугольник АВС со сторонами АВ=25, АС=7, ВС=24. На Трен. раб. 25. 01. 12 Дан треугольник АВС со сторонами АВ=25, АС=7, ВС=24. На стороне ВС взята точка D, а на отрезке AD – точка О, причем СD=8 и АО=3 ОD. Окружность с центром О проходит через точку С. Найдите расстояние от точки С до точки пересечения этой окружности с прямой АВ. B T M Q D O M 1 N A C T B M 1 Q D C O N A

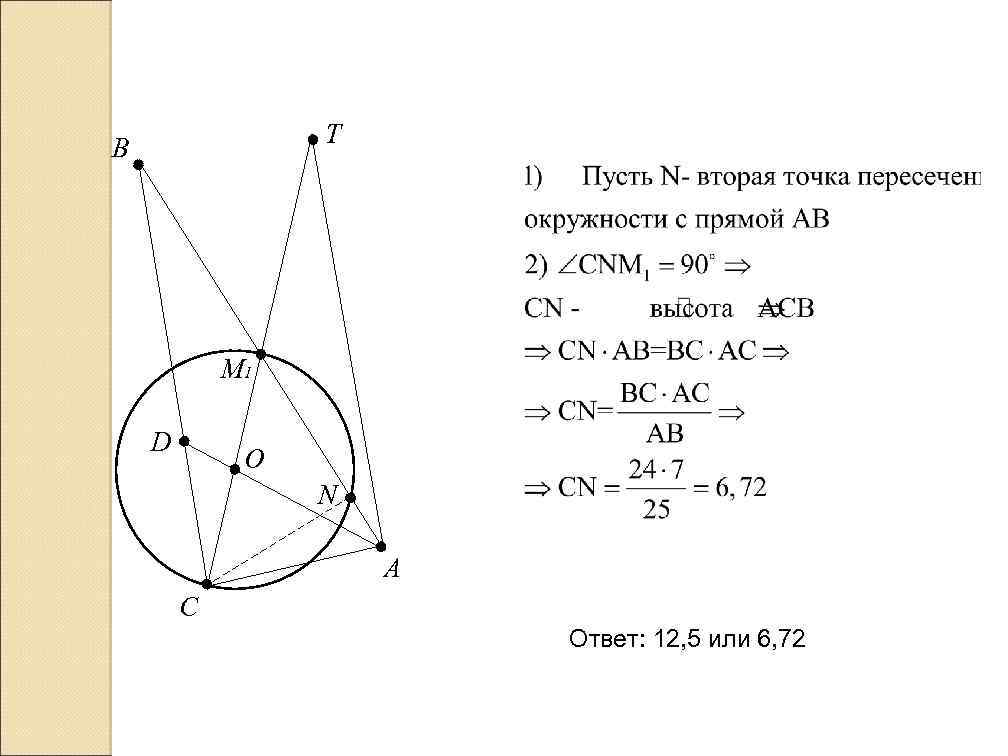T B M 1 D O N A C Ответ: 12, 5 или 6, T B M 1 D O N A C Ответ: 12, 5 или 6, 72