ed83ce041e82a6a4ead8a79d21a5829a.ppt
- Количество слайдов: 32
 Ryan O’Donnell - Microsoft Mike Saks - Rutgers Oded Schramm - Microsoft Rocco Servedio - Columbia
Ryan O’Donnell - Microsoft Mike Saks - Rutgers Oded Schramm - Microsoft Rocco Servedio - Columbia
 Part I: Decision trees have large influences
Part I: Decision trees have large influences
 Printer troubleshooter Does anything print? Can print from Notepad? Network printer? Right size paper? File too complicated? Printer mis-setup? Driver OK? Solved Call tech support Solved
Printer troubleshooter Does anything print? Can print from Notepad? Network printer? Right size paper? File too complicated? Printer mis-setup? Driver OK? Solved Call tech support Solved
 Decision tree complexity f : {Attr 1} × {Attr 2} × ∙∙∙ × {Attrn} → {− 1, 1}. What’s the “best” DT for f, and how to find it? Depth Expected depth = worst case # of questions. = avg. # of questions.
Decision tree complexity f : {Attr 1} × {Attr 2} × ∙∙∙ × {Attrn} → {− 1, 1}. What’s the “best” DT for f, and how to find it? Depth Expected depth = worst case # of questions. = avg. # of questions.
 Building decision trees 1. Identify the most ‘influential’/‘decisive’/‘relevant’ variable. 2. Put it at the root. 3. Recursively build DTs for its children. Almost all real-world learning algs based on this – CART, C 4. 5, … Almost no theoretical (PAC-style) learning algs based on this – [Blum 92, KM 93, BBVKV 97, PTF-folklore, OS 04] – no; [EH 89, SJ 03] – sorta. Conj’d to be good for some problems (e. g. , percolation [SS 04]) but unprovable…
Building decision trees 1. Identify the most ‘influential’/‘decisive’/‘relevant’ variable. 2. Put it at the root. 3. Recursively build DTs for its children. Almost all real-world learning algs based on this – CART, C 4. 5, … Almost no theoretical (PAC-style) learning algs based on this – [Blum 92, KM 93, BBVKV 97, PTF-folklore, OS 04] – no; [EH 89, SJ 03] – sorta. Conj’d to be good for some problems (e. g. , percolation [SS 04]) but unprovable…
 Boolean DTs f : {− 1, 1}n → {− 1, 1}. x 1 x 2 Maj 3 − 1 x 2 x 3 − 1 x 3 1 − 1 1 1 D(f) = min depth of a DT for f. 0 ≤ D(f) ≤ n.
Boolean DTs f : {− 1, 1}n → {− 1, 1}. x 1 x 2 Maj 3 − 1 x 2 x 3 − 1 x 3 1 − 1 1 1 D(f) = min depth of a DT for f. 0 ≤ D(f) ≤ n.
 Boolean DTs • {− 1, 1}n viewed as a probability space, with uniform probability distribution. • uniformly random path down a DT, plus a uniformly random setting of the unqueried variables, defines a uniformly random input • expected depth : δ(f).
Boolean DTs • {− 1, 1}n viewed as a probability space, with uniform probability distribution. • uniformly random path down a DT, plus a uniformly random setting of the unqueried variables, defines a uniformly random input • expected depth : δ(f).
 Influences influence of coordinate j on f = the probability that xj is relevant for f Ij(f) = Pr[ f(x) ≠ f(x (⊕j) ) ]. 0 ≤ Ij(f) ≤ 1.
Influences influence of coordinate j on f = the probability that xj is relevant for f Ij(f) = Pr[ f(x) ≠ f(x (⊕j) ) ]. 0 ≤ Ij(f) ≤ 1.
 Main question: If a function f has a “shallow” decision tree, does it have a variable with “significant” influence?
Main question: If a function f has a “shallow” decision tree, does it have a variable with “significant” influence?
 Main question: No. But for a silly reason: Suppose f is highly biased; say Pr[f = 1] = p ≪ 1. Then for any j, Ij(f) = Pr[f(x) = 1, f(x( j)) = − 1] + Pr[f(x) = − 1, f(x( j)) = 1] ≤ Pr[f(x) = 1] + Pr[f(x( j)) = 1] ≤ p+p = 2 p.
Main question: No. But for a silly reason: Suppose f is highly biased; say Pr[f = 1] = p ≪ 1. Then for any j, Ij(f) = Pr[f(x) = 1, f(x( j)) = − 1] + Pr[f(x) = − 1, f(x( j)) = 1] ≤ Pr[f(x) = 1] + Pr[f(x( j)) = 1] ≤ p+p = 2 p.
![Variance ⇒ Influences are always at most 2 min{p, q}. Analytically nicer expression: Var[f]. Variance ⇒ Influences are always at most 2 min{p, q}. Analytically nicer expression: Var[f].](https://present5.com/presentation/ed83ce041e82a6a4ead8a79d21a5829a/image-11.jpg) Variance ⇒ Influences are always at most 2 min{p, q}. Analytically nicer expression: Var[f]. • Var[f] = E[f 2] – E[f]2 = 1 – (p – q)2 = 1 – (2 p − 1)2 = 4 p(1 – p) = 4 pq. • 2 min{p, q} ≤ 4 pq ≤ 4 min{p, q}. • It’s 1 for balanced functions. So Ij(f) ≤ Var[f], and it is fair to say Ij(f) is “significant” if it’s a significant fraction of Var[f].
Variance ⇒ Influences are always at most 2 min{p, q}. Analytically nicer expression: Var[f]. • Var[f] = E[f 2] – E[f]2 = 1 – (p – q)2 = 1 – (2 p − 1)2 = 4 p(1 – p) = 4 pq. • 2 min{p, q} ≤ 4 pq ≤ 4 min{p, q}. • It’s 1 for balanced functions. So Ij(f) ≤ Var[f], and it is fair to say Ij(f) is “significant” if it’s a significant fraction of Var[f].
 Main question: If a function f has a “shallow” decision tree, does it have a variable with influence at least a “significant” fraction of Var[f]?
Main question: If a function f has a “shallow” decision tree, does it have a variable with influence at least a “significant” fraction of Var[f]?
![Notation τ(d) = min f : D(f) ≤ d max { Ij(f) / Var[f] Notation τ(d) = min f : D(f) ≤ d max { Ij(f) / Var[f]](https://present5.com/presentation/ed83ce041e82a6a4ead8a79d21a5829a/image-13.jpg) Notation τ(d) = min f : D(f) ≤ d max { Ij(f) / Var[f] }. j
Notation τ(d) = min f : D(f) ≤ d max { Ij(f) / Var[f] }. j
 Known lower bounds Suppose f : {− 1, 1}n → {− 1, 1}. • An elementary old inequality states Var[f] ≤ n Σ j=1 Ij(f). Thus f has a variable with influence at least Var[f]/n. • A deep inequality of [KKL 88] shows there is always a coord. j such that Ij(f) ≥ Var[f] ∙ Ω(log n / n). If D(f) = d then f really has at most 2 d variables. Hence we get τ(d) ≥ 1/2 d from the first, and τ(d) ≥ Ω(d/2 d) from KKL.
Known lower bounds Suppose f : {− 1, 1}n → {− 1, 1}. • An elementary old inequality states Var[f] ≤ n Σ j=1 Ij(f). Thus f has a variable with influence at least Var[f]/n. • A deep inequality of [KKL 88] shows there is always a coord. j such that Ij(f) ≥ Var[f] ∙ Ω(log n / n). If D(f) = d then f really has at most 2 d variables. Hence we get τ(d) ≥ 1/2 d from the first, and τ(d) ≥ Ω(d/2 d) from KKL.
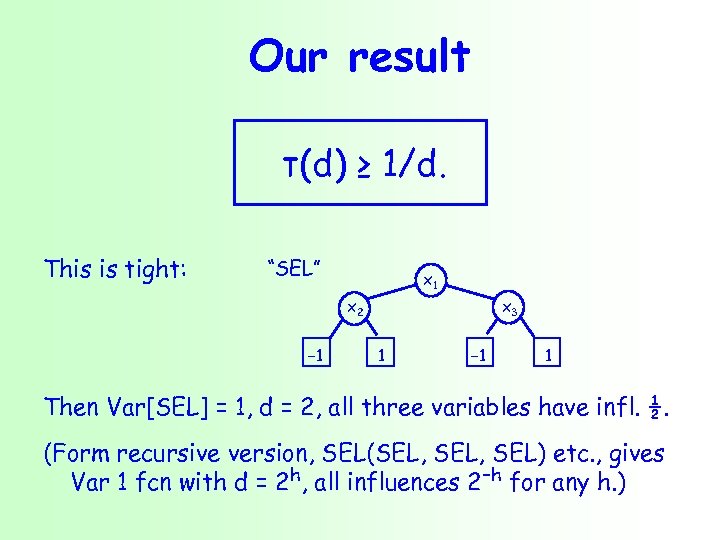 Our result τ(d) ≥ 1/d. This is tight: “SEL” x 1 x 2 − 1 x 3 1 − 1 1 Then Var[SEL] = 1, d = 2, all three variables have infl. ½. (Form recursive version, SEL(SEL, SEL) etc. , gives Var 1 fcn with d = 2 h, all influences 2−h for any h. )
Our result τ(d) ≥ 1/d. This is tight: “SEL” x 1 x 2 − 1 x 3 1 − 1 1 Then Var[SEL] = 1, d = 2, all three variables have infl. ½. (Form recursive version, SEL(SEL, SEL) etc. , gives Var 1 fcn with d = 2 h, all influences 2−h for any h. )
 Our actual main theorem Given a decision tree f, let δj(f) = Pr[tree queries xj]. Then n Var[f] ≤ Σ δj(f) Ij(f). j=1 Cor: Fix the tree with smallest expected depth. Then n Σ δj(f) = E[depth of a path] =: δ(f) ≤ D(f). j=1 n ⇒ Var[f] ≤ max Ij ∙ Σ δj = max Ij ∙ δ(f) ⇒ max Ij ≥ Var[f] / δ(f) ≥ Var[f] / D(f). j=1
Our actual main theorem Given a decision tree f, let δj(f) = Pr[tree queries xj]. Then n Var[f] ≤ Σ δj(f) Ij(f). j=1 Cor: Fix the tree with smallest expected depth. Then n Σ δj(f) = E[depth of a path] =: δ(f) ≤ D(f). j=1 n ⇒ Var[f] ≤ max Ij ∙ Σ δj = max Ij ∙ δ(f) ⇒ max Ij ≥ Var[f] / δ(f) ≥ Var[f] / D(f). j=1
 Proof Pick a random path in the tree. This gives some set of variables, P = (x. J 1, … , x. JT), along with an assignment to them, βP. Call the remaining set of variables P and pick a random assignment βP for them too. Let X be the (uniformly random string) given by combining these two assignments, (βP, βP). Also, define JT+1, … , Jn = ┴.
Proof Pick a random path in the tree. This gives some set of variables, P = (x. J 1, … , x. JT), along with an assignment to them, βP. Call the remaining set of variables P and pick a random assignment βP for them too. Let X be the (uniformly random string) given by combining these two assignments, (βP, βP). Also, define JT+1, … , Jn = ┴.
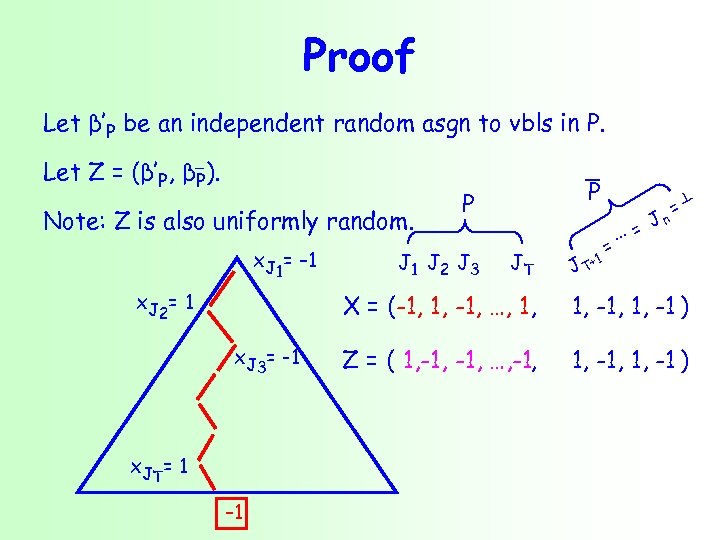 Proof Let β’P be an independent random asgn to vbls in P. Let Z = (β’P, βP). Note: Z is also uniformly random. x. J 1= – 1 x J 2 = 1 P P J 1 J 2 J 3 JT ∙∙ = 1 J T+ =∙ Jn =┴ X = (-1, 1, -1, …, 1, x. J 3= -1 x JT = 1 – 1 1, -1, 1, -1 ) Z = ( 1, -1, …, -1, 1, -1, 1, -1 )
Proof Let β’P be an independent random asgn to vbls in P. Let Z = (β’P, βP). Note: Z is also uniformly random. x. J 1= – 1 x J 2 = 1 P P J 1 J 2 J 3 JT ∙∙ = 1 J T+ =∙ Jn =┴ X = (-1, 1, -1, …, 1, x. J 3= -1 x JT = 1 – 1 1, -1, 1, -1 ) Z = ( 1, -1, …, -1, 1, -1, 1, -1 )
 Proof Finally, for t = 0…T, let Yt be the same string as X, except that Z’s assignments (β’P) for variables x. J 1, … , x. Jt are swapped in. Note: Y 0 = X, YT = Z. Y 0 = X = (-1, 1, -1, …, 1, -1, 1, -1 ) Y 1 = ( 1, 1, -1, …, 1, -1, 1, -1 ) Y 2 = ( 1, -1, …, 1, -1, 1, -1 ) ∙∙∙∙ YT = Z = ( 1, -1, …, -1, Also define YT+1 = ∙ ∙ ∙ = Yn = Z. 1, -1, 1, -1 )
Proof Finally, for t = 0…T, let Yt be the same string as X, except that Z’s assignments (β’P) for variables x. J 1, … , x. Jt are swapped in. Note: Y 0 = X, YT = Z. Y 0 = X = (-1, 1, -1, …, 1, -1, 1, -1 ) Y 1 = ( 1, 1, -1, …, 1, -1, 1, -1 ) Y 2 = ( 1, -1, …, 1, -1, 1, -1 ) ∙∙∙∙ YT = Z = ( 1, -1, …, -1, Also define YT+1 = ∙ ∙ ∙ = Yn = Z. 1, -1, 1, -1 )
![Var[f] = E[f 2] – E[f]2 = E[ f(X) ] – E[ f(X)f(Z) ] Var[f] = E[f 2] – E[f]2 = E[ f(X) ] – E[ f(X)f(Z) ]](https://present5.com/presentation/ed83ce041e82a6a4ead8a79d21a5829a/image-20.jpg) Var[f] = E[f 2] – E[f]2 = E[ f(X) ] – E[ f(X)f(Z) ] = E[ f(X)f(Y 0) – f(X)f(Yn) ] = E[ ≤ = = = E[ Σ f(X) (f(Yt− 1) – f(Yt)) ] Σ |f(Yt− 1) – f(Yt)| ] t = 1. . n Σ 2 Pr[f(Yt− 1) ≠ f(Yt)] t = 1. . n Σ j = 1. . n Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] Σ Σ Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] j = 1. . n t = 1. . n
Var[f] = E[f 2] – E[f]2 = E[ f(X) ] – E[ f(X)f(Z) ] = E[ f(X)f(Y 0) – f(X)f(Yn) ] = E[ ≤ = = = E[ Σ f(X) (f(Yt− 1) – f(Yt)) ] Σ |f(Yt− 1) – f(Yt)| ] t = 1. . n Σ 2 Pr[f(Yt− 1) ≠ f(Yt)] t = 1. . n Σ j = 1. . n Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] Σ Σ Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] j = 1. . n t = 1. . n
 Proof … = Σ j = 1. . n Σ t = 1. . n Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] Utterly Crucial Observation: Conditioned on Jt = j, (Yt− 1, Yt) are jointly distributed exactly as (W, W’), where W is uniformly random, and W’ is W with jth bit rerandomized.
Proof … = Σ j = 1. . n Σ t = 1. . n Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] Utterly Crucial Observation: Conditioned on Jt = j, (Yt− 1, Yt) are jointly distributed exactly as (W, W’), where W is uniformly random, and W’ is W with jth bit rerandomized.
 P P x. J 1= – 1 x J 2 = 1 J 2 J 3 JT ∙∙ = 1 J T+ =∙ Jn =┴ X = (-1, 1, -1, …, 1, x J 3 = 1 1, -1, 1, -1 ) Z = ( 1, -1, …, -1, 1, -1, 1, -1 ) x JT = 1 – 1 Y 0 = X = (-1, 1, -1, …, 1, -1, 1, -1 ) Y 1 = ( 1, 1, -1, …, 1, -1, 1, -1 ) Y 2 = ( 1, -1, …, 1, -1, 1, -1 ) ∙∙∙∙ YT = Z = ( 1, -1, …, -1, 1, -1, 1, -1 )
P P x. J 1= – 1 x J 2 = 1 J 2 J 3 JT ∙∙ = 1 J T+ =∙ Jn =┴ X = (-1, 1, -1, …, 1, x J 3 = 1 1, -1, 1, -1 ) Z = ( 1, -1, …, -1, 1, -1, 1, -1 ) x JT = 1 – 1 Y 0 = X = (-1, 1, -1, …, 1, -1, 1, -1 ) Y 1 = ( 1, 1, -1, …, 1, -1, 1, -1 ) Y 2 = ( 1, -1, …, 1, -1, 1, -1 ) ∙∙∙∙ YT = Z = ( 1, -1, …, -1, 1, -1, 1, -1 )
![Proof … = = = Σ Σ Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) Proof … = = = Σ Σ Pr[Jt = j] ∙ 2 Pr[f(Yt− 1)](https://present5.com/presentation/ed83ce041e82a6a4ead8a79d21a5829a/image-23.jpg) Proof … = = = Σ Σ Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] j = 1. . n Σ t = 1. . n Pr[Jt = j] ∙ 2 Pr[f(W) ≠ f(W’)] Σ Σ Pr[Jt = j] ∙ Ij(f) j = 1. . n Σ j = 1. . n t = 1. . n Σ Ij ∙ Σ I j δ j. j = 1. . n Σ Pr[Jt = j] t = 1. . n
Proof … = = = Σ Σ Pr[Jt = j] ∙ 2 Pr[f(Yt− 1) ≠ f(Yt) | Jt = j] j = 1. . n Σ t = 1. . n Pr[Jt = j] ∙ 2 Pr[f(W) ≠ f(W’)] Σ Σ Pr[Jt = j] ∙ Ij(f) j = 1. . n Σ j = 1. . n t = 1. . n Σ Ij ∙ Σ I j δ j. j = 1. . n Σ Pr[Jt = j] t = 1. . n
 Part II: Lower bounds for monotone graph properties
Part II: Lower bounds for monotone graph properties
 Monotone graph properties Consider graphs on v vertices; let n = v (2 ). “Nontrivial monotone graph property”: • “nontrivial property”: a (nonempty, nonfull) subset of all v-vertex graphs • “graph property”: closed under permutations of the vertices ( no edge is ‘distinguished’) • monotone: adding edges can only put you into the property, not take you out e. g. : Contains-A-Triangle, Connected, Has-Hamiltonian. Path, Non-Planar, Has-at-least-n/2 -edges, …
Monotone graph properties Consider graphs on v vertices; let n = v (2 ). “Nontrivial monotone graph property”: • “nontrivial property”: a (nonempty, nonfull) subset of all v-vertex graphs • “graph property”: closed under permutations of the vertices ( no edge is ‘distinguished’) • monotone: adding edges can only put you into the property, not take you out e. g. : Contains-A-Triangle, Connected, Has-Hamiltonian. Path, Non-Planar, Has-at-least-n/2 -edges, …
![Aanderaa-Karp-Rosenberg conj. Every nontrivial monotone graph propery has D(f) = n. [Rivest-Vuillemin-75]: ≥ v Aanderaa-Karp-Rosenberg conj. Every nontrivial monotone graph propery has D(f) = n. [Rivest-Vuillemin-75]: ≥ v](https://present5.com/presentation/ed83ce041e82a6a4ead8a79d21a5829a/image-26.jpg) Aanderaa-Karp-Rosenberg conj. Every nontrivial monotone graph propery has D(f) = n. [Rivest-Vuillemin-75]: ≥ v 2/16. [Kleitman-Kwiatowski-80] ≥ v 2/9. [Kahn-Saks-Sturtevant-84] ≥ n/2, = n, if v is a prime power. [Topology + group theory!] [Yao-88] = n in the bipartite case.
Aanderaa-Karp-Rosenberg conj. Every nontrivial monotone graph propery has D(f) = n. [Rivest-Vuillemin-75]: ≥ v 2/16. [Kleitman-Kwiatowski-80] ≥ v 2/9. [Kahn-Saks-Sturtevant-84] ≥ n/2, = n, if v is a prime power. [Topology + group theory!] [Yao-88] = n in the bipartite case.
 Randomized DTs • Have ‘coin flip’ nodes in the trees that cost nothing. • Or, probability distribution over deterministic DTs. Note: We want both 0 -sided error and worst-case input. R(f) = min, over randomized DTs that compute f with 0 error, of max over inputs x, of expected # of queries. The expectation is only over the DT’s internal coins.
Randomized DTs • Have ‘coin flip’ nodes in the trees that cost nothing. • Or, probability distribution over deterministic DTs. Note: We want both 0 -sided error and worst-case input. R(f) = min, over randomized DTs that compute f with 0 error, of max over inputs x, of expected # of queries. The expectation is only over the DT’s internal coins.
 Maj 3: D(Maj 3) = 3. Pick two inputs at random, check if they’re the same. If not, check the 3 rd. R(Maj 3) ≤ 8/3. Let f = recursive-Maj 3 [Maj 3 (Maj 3 , Maj 3 ), etc…] For depth-h version (n = 3 h), D(f) = 3 h. R(f) ≤ (8/3)h. (Not best possible…!)
Maj 3: D(Maj 3) = 3. Pick two inputs at random, check if they’re the same. If not, check the 3 rd. R(Maj 3) ≤ 8/3. Let f = recursive-Maj 3 [Maj 3 (Maj 3 , Maj 3 ), etc…] For depth-h version (n = 3 h), D(f) = 3 h. R(f) ≤ (8/3)h. (Not best possible…!)
 Randomized AKR / Yao conjectured in ’ 77 that every nontrivial monotone graph property f has R(f) ≥ Ω(v 2). Lower bound Ω( ∙ ) v v log Who [Yao-77] 1/12 v [Yao-87] v 5/4 [King-88] v 4/3 [Hajnal-91] v 4/3 log 1/3 v min{ v/p, v 2/log v } v 4/3 / p 1/3 [Chakrabarti-Khot-01] [Fried. -Kahn-Wigd. -02] [us]
Randomized AKR / Yao conjectured in ’ 77 that every nontrivial monotone graph property f has R(f) ≥ Ω(v 2). Lower bound Ω( ∙ ) v v log Who [Yao-77] 1/12 v [Yao-87] v 5/4 [King-88] v 4/3 [Hajnal-91] v 4/3 log 1/3 v min{ v/p, v 2/log v } v 4/3 / p 1/3 [Chakrabarti-Khot-01] [Fried. -Kahn-Wigd. -02] [us]
 Outline • Extend main inequality to the p-biased case. (Then LHS is 1. ) • Use Yao’s minmax principle: Show that under p-biased {− 1, 1} n, δ = Σ δj = avg # queries is large for any tree. • Main inequality: max influence is small ⇒ δ is large. • Graph property all vbls have the same influence. • Hence: sum of influences is small ⇒ δ is large. • [OS 04]: f monotone ⇒ sum of influences ≤ √δ. • Hence: sum of influences is large ⇒ δ is large. • So either way, δ is large.
Outline • Extend main inequality to the p-biased case. (Then LHS is 1. ) • Use Yao’s minmax principle: Show that under p-biased {− 1, 1} n, δ = Σ δj = avg # queries is large for any tree. • Main inequality: max influence is small ⇒ δ is large. • Graph property all vbls have the same influence. • Hence: sum of influences is small ⇒ δ is large. • [OS 04]: f monotone ⇒ sum of influences ≤ √δ. • Hence: sum of influences is large ⇒ δ is large. • So either way, δ is large.
![Generalizing the inequality Var[f] ≤ n Σ δj(f) Ij(f). j=1 Generalizations (which basically require Generalizing the inequality Var[f] ≤ n Σ δj(f) Ij(f). j=1 Generalizations (which basically require](https://present5.com/presentation/ed83ce041e82a6a4ead8a79d21a5829a/image-31.jpg) Generalizing the inequality Var[f] ≤ n Σ δj(f) Ij(f). j=1 Generalizations (which basically require no proof change): • holds for randomized DTs • holds for randomized “subcube partitions” • holds for functions on any product probability space f : Ω 1 × ∙∙∙ × Ωn → {− 1, 1} (with notion of “influence” suitably generalized) • holds for real-valued functions with (necessary) loss of a factor, at most √δ
Generalizing the inequality Var[f] ≤ n Σ δj(f) Ij(f). j=1 Generalizations (which basically require no proof change): • holds for randomized DTs • holds for randomized “subcube partitions” • holds for functions on any product probability space f : Ω 1 × ∙∙∙ × Ωn → {− 1, 1} (with notion of “influence” suitably generalized) • holds for real-valued functions with (necessary) loss of a factor, at most √δ
 Closing thought It’s funny that our bound gets stuck roughly at the same level as Hajnal / Chakrabarti-Khot, n 2/3 = v 4/3. Note that n 2/3 [I believe] cannot be improved by more than a log factor merely for monotone transitive functions, due to [BSW 04]. Thus to get better than v 4/3 for monotone graph properties, you must use the fact that it’s a graph property. Chakrabarti-Khot does definitely use the fact that it’s a graph property (all sorts of graph packing lemmas). Or do they? Since they get stuck at essentially v 4/3, I wonder if there’s any chance their result doesn’t truly need the fact that it’s a graph property…
Closing thought It’s funny that our bound gets stuck roughly at the same level as Hajnal / Chakrabarti-Khot, n 2/3 = v 4/3. Note that n 2/3 [I believe] cannot be improved by more than a log factor merely for monotone transitive functions, due to [BSW 04]. Thus to get better than v 4/3 for monotone graph properties, you must use the fact that it’s a graph property. Chakrabarti-Khot does definitely use the fact that it’s a graph property (all sorts of graph packing lemmas). Or do they? Since they get stuck at essentially v 4/3, I wonder if there’s any chance their result doesn’t truly need the fact that it’s a graph property…


