Ряды распределения Ряд распределения это упорядоченное распределение

Ряды распределения

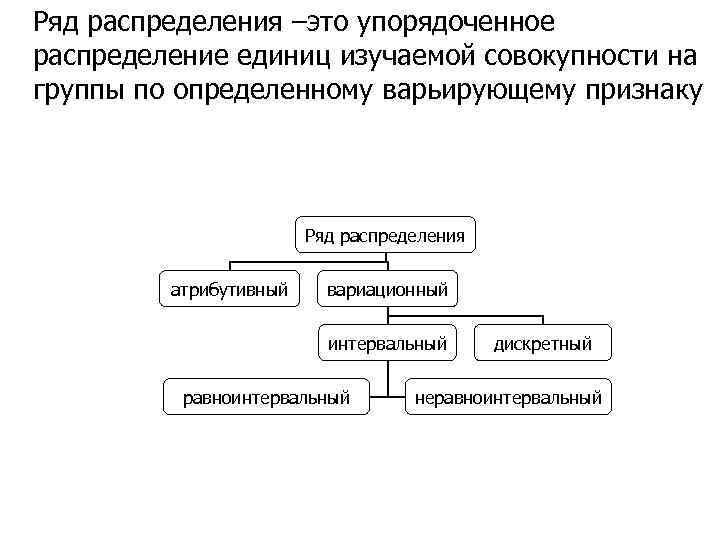Ряд распределения –это упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку Ряд распределения атрибутивный вариационный интервальный равноинтервальный дискретный неравноинтервальный

Атрибутивные ряды распределения это ряды распределения, построенные по качественным признакам, т. е. признакам, не имеющим числового выражения. Они характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов эти данные позволяют исследовать изменение структуры. Примером атрибутивного ряда распределения может служить распределение студентов группы по полу.

Вариационные рады в зависимости от характера вариации подразделяются на дискретные и интервальные. Дискретные вариационные рады основаны на дискретных (прерывных) признаках, имеющих только целые значения (например, тарифный разряд рабочих, число детей в семье); интервальные — на непрерывных признаках (имеющих любые значения, в том числе и дробные

Вариационные ряды распределения состоят из двух элементов: вариантов (Х) и частот(f) • Числовые значения количественного признака в вариационном ряду распределения называются вариантами. Они могут быть положительными и отрицательными (прибыль и убыток), абсолютными и относительными. • Частоты — это численности отдельных вариант или каждой группы вариационного ряда, т. е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот называется объемом совокупности. • Частости — это частоты, выраженные в виде относительных величин (долях единиц или процентах). Сумма частостей равна единице или 100%. Замена частот частостями позволяет сопоставлять вариационные ряды с разным числом наблюдений.

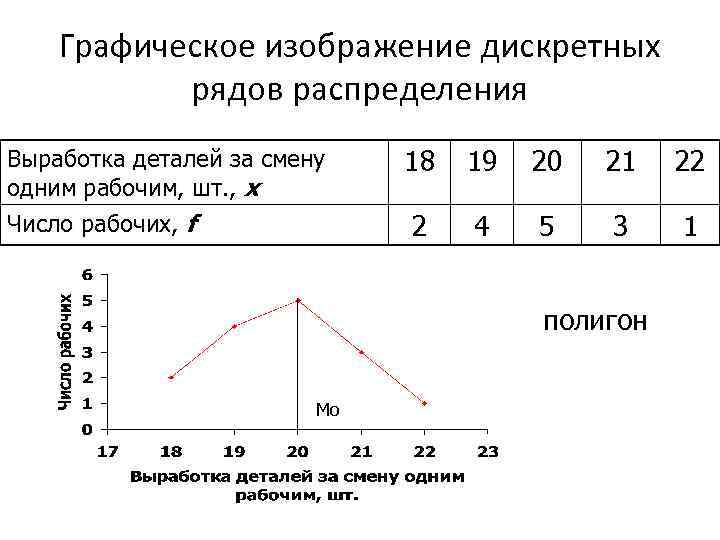Графическое изображение дискретных рядов распределения Выработка деталей за смену одним рабочим, шт. , x Число рабочих, f 18 19 20 21 22 2 4 5 3 1 полигон Мо

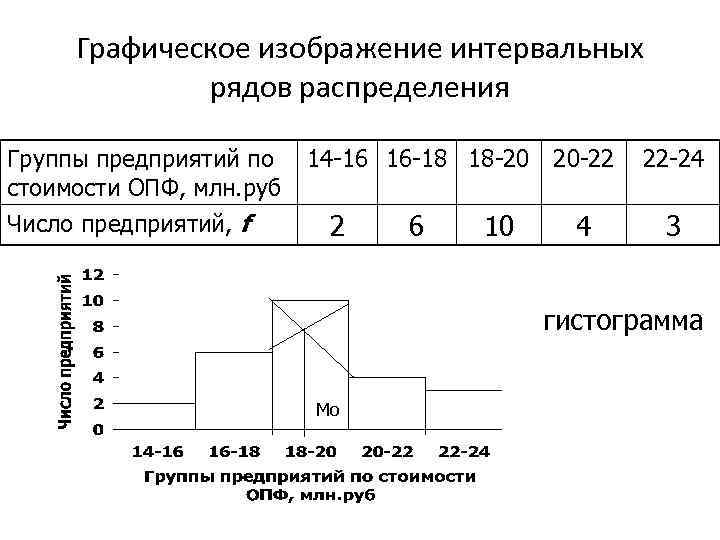Графическое изображение интервальных рядов распределения Группы предприятий по стоимости ОПФ, млн. руб Число предприятий, f 14 -16 16 -18 18 -20 20 -22 2 6 10 4 22 -24 3 гистограмма Мо

СТРУКТУРНЫЕ СРЕДНИЕ • Мода (Мо)– это значение признака, повторяющееся в совокупности с наибольшей частотой, т. е. отражает наиболее часто распространенный вариант значения признака. Поэтому графически мода изображается на полигоне или гистограмме. • Медиана – это значение признака, приходящееся на середину ранжированной совокупности. Поэтому графически медиана изображается на кумуляте или огиве. Для определения медианного значения признака находят номер медианной единицы ряда, используя формулу: где n – объем совокупности.

МОДА где хмо – нижняя граница модального интервала, h. Мо –величина модального интервала, f. Мо – частота модального интервала, f. Мо-1 – частота интервала, предшествующего модальному, f. Мо+1 – частота интервала, следующего за модальным.

МЕДИАНА где х. Ме – нижняя граница медианного интервала, h. Ме –величина медианного интервала, f. Ме – частота медианного интервала, SМе-1 – накопленная частота интервала, предшествующего медианному

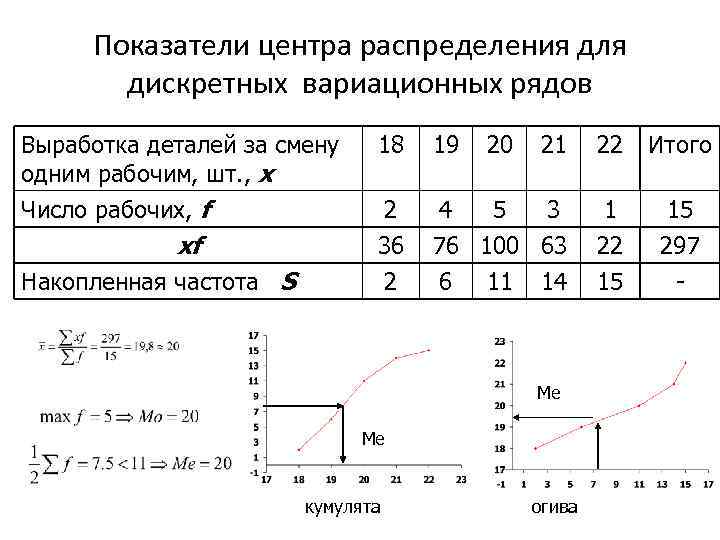Показатели центра распределения для дискретных вариационных рядов Выработка деталей за смену одним рабочим, шт. , x Число рабочих, f xf Накопленная частота S 18 19 20 21 2 36 2 4 5 3 76 100 63 6 11 14 Me Me кумулята огива 22 Итого 1 22 15 15 297 -

Выводы по показателям центра распределения: • Х: В среднем один рабочий за смену производит 20 деталей • Мо: Большинство рабочих за смену производит 20 деталей • Ме: Первые 7 рабочих за смену производят не более 20 деталей, а последние 7 рабочих за смену производят не менее 20 деталей. 7 -ой рабочий за смену производит 20 деталей

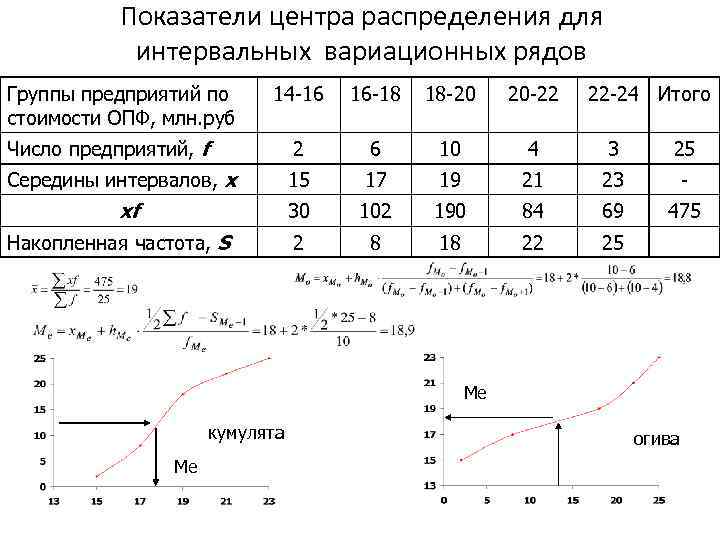Показатели центра распределения для интервальных вариационных рядов Группы предприятий по стоимости ОПФ, млн. руб 14 -16 16 -18 18 -20 20 -22 Число предприятий, f 2 6 10 4 3 25 Середины интервалов, х 15 17 19 21 23 - 30 102 190 84 69 475 2 8 18 22 25 xf Накопленная частота, S 22 -24 Итого Me кумулята Me огива

Выводы по показателям центра распределения: • Х: В среднем основные фонды на предприятии стоят 19 млн. руб. • Мо: На большинстве предприятий основные фонды стоят 18, 8 млн. руб. • Ме: На первых 12 предприятиях основные фонды стоят не более 18, 9 млн. руб. , а на последних 12 предприятиях основные фонды стоят не менее 18, 9 млн. руб. . 13 -ое предприятие имеет основные фонды на сумму 18, 9 млн. руб.

Показатели вариации Абсолютные: • Размах вариации Относительные: • Коэффициент осцилляции • Среднее линейное отклонение • Относительное линейное отклонение • Дисперсия • Коэффициент вариации колеблемость Слабая <10% • Среднеквадратичное отклонение Умеренная 10 -25 Сильная>25 Однородность совокупности -33%

Показатели формы распределения • Коэффициент асимметрии • Эксцесс Если As >0, то распределение имеет правостороннюю асимметрию Если As < 0, то распределение имеет левостороннюю асимметрию. Если As =0 ( х = Мо = Ме), то распределение симметричное Если|As |<0. 5 – асимметрия незначительная Если|As |>0. 5 – асимметрия сильная Если Ех >0, то распределение островершинное Если Ех< 0, то распределение плосковершинное

Показатели вариации Абсолютные: • Размах вариации Относительные: • Коэффициент осцилляции • Среднее линейное отклонение • Относительное линейное отклонение • Дисперсия • Среднеквадратичное отклонение • Коэффициент вариации колеблемость Слабая <10% Умеренная 10 -25 Сильная>25 Однородность совокупности -33% • Коэффициент асимметрии

Выводы по показателям вариации: • R: стоимость основных фондов колеблется в пределах от 14 до 24 млн. руб. • КR: крайние значения составляют от средней стоимости основных фондов 53% • d: средневзвешенное отклонение от средней стоимости основных фондов в ту и другую сторону составляет 1. 6 млн. руб. • Kd: средневзвешенное отклонение от средней стоимости основных фондов составляет 8, 4% от средней стоимости основных фондов • As: распределение имеет правостороннюю асимметрию, т. к. As >0 Если As < 0, то распределение имеет левостороннюю асимметрию. Если As =0 ( х = Мо = Ме), то распределение симметричное.

Выводы по наиболее важным показателям вариации: • σ=2. 19: средневзвешенный квадрат отклонения от средней стоимости основных фондов в ту и другую сторону составляет 2, 19 млн. руб. • V=11. 5% 1. 10 < 11. 5 < 25 Значит изменение стоимости основных фондов умеренное 2. 11. 5 < 33 Значит совокупность однородная

Алгоритм расчета среднеквадратического отклонения: – находим среднюю арифметическую ряда ( ); – находим отклонение каждой варианты от средней арифметической ( ); – возводим каждое отклонение в квадрат ( )2; – умножаем каждый квадрат отклонений на соответствующий вес ( )2 fi; – суммируем все произведения ( )2 fi; – делим сумму произведений на сумму частот и получаем дисперсию ; – извлекаем квадратный корень из частного и получаем среднеквадратическое отклонение

Номер интервала 1 2 3 4 Границы интервала Стажа работы до 5 5 -8 8 - 13 Свыше 13 Количество сотрудников 24 30 40 6

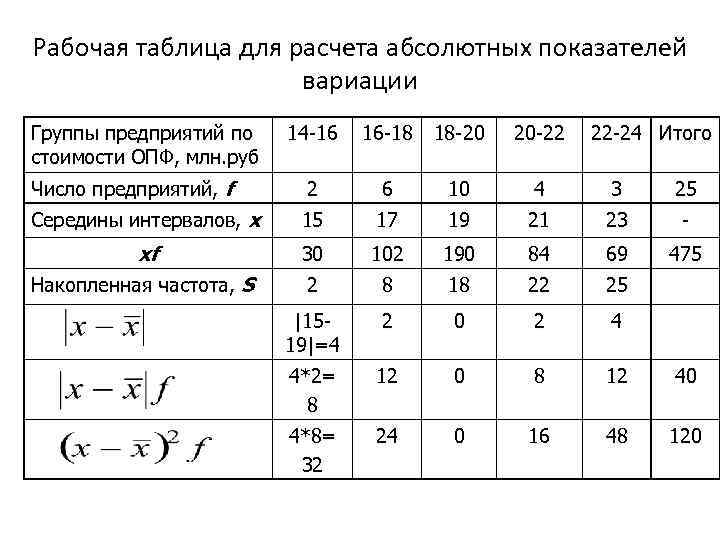Рабочая таблица для расчета абсолютных показателей вариации Группы предприятий по стоимости ОПФ, млн. руб 14 -16 16 -18 18 -20 20 -22 22 -24 Итого Число предприятий, f 2 6 10 4 3 25 Середины интервалов, х 15 17 19 21 23 - xf 30 102 190 84 69 475 Накопленная частота, S 2 8 18 22 25 |1519|=4 2 0 2 4 4*2= 8 12 0 8 12 40 4*8= 32 24 0 16 48 120

Анализ сроков и объемов поставки • Равномерность поставки – это поступление товара равными партиями через равные промежутки времени (ρ=1 -V). • Ритмичность поставки – это соблюдение сроков и объемов поставки, оговоренных контрактом с учетом сезонных и цикличных особенностей производства, продажи или потребления (Каритм).

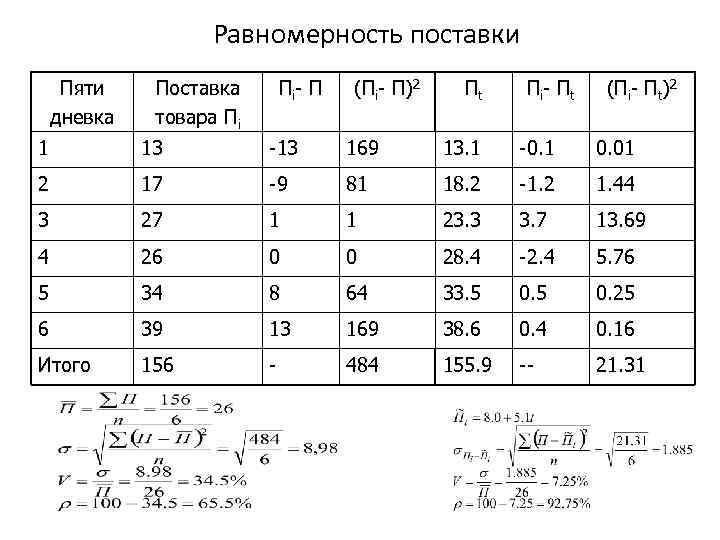Равномерность поставки Пяти дневка Поставка товара Пi Пi- П (Пi- П)2 Пt Пi- Пt (Пi- Пt)2 1 13 -13 169 13. 1 -0. 1 0. 01 2 17 -9 81 18. 2 -1. 2 1. 44 3 27 1 1 23. 3 3. 7 13. 69 4 26 0 0 28. 4 -2. 4 5. 76 5 34 8 64 33. 5 0. 25 6 39 13 169 38. 6 0. 4 0. 16 Итого 156 - 484 155. 9 -- 21. 31

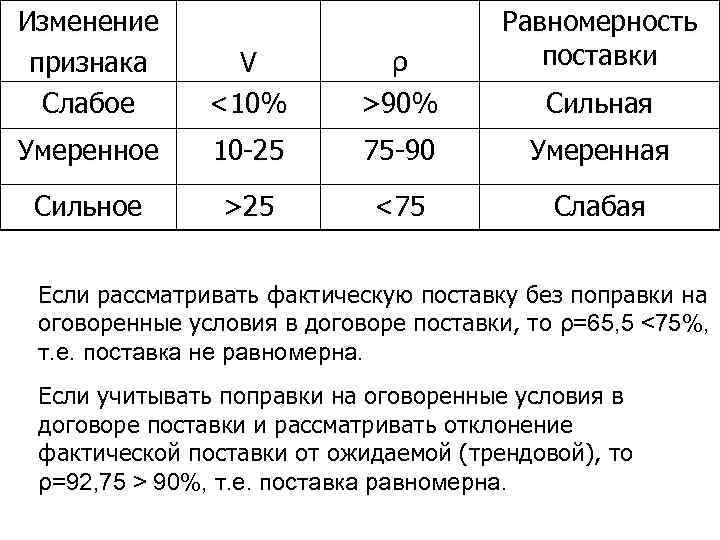Изменение признака Слабое Равномерность поставки V <10% ρ >90% Умеренное 10 -25 75 -90 Умеренная Сильное >25 <75 Слабая Сильная Если рассматривать фактическую поставку без поправки на оговоренные условия в договоре поставки, то ρ=65, 5 <75%, т. е. поставка не равномерна. Если учитывать поправки на оговоренные условия в договоре поставки и рассматривать отклонение фактической поставки от ожидаемой (трендовой), то ρ=92, 75 > 90%, т. е. поставка равномерна.

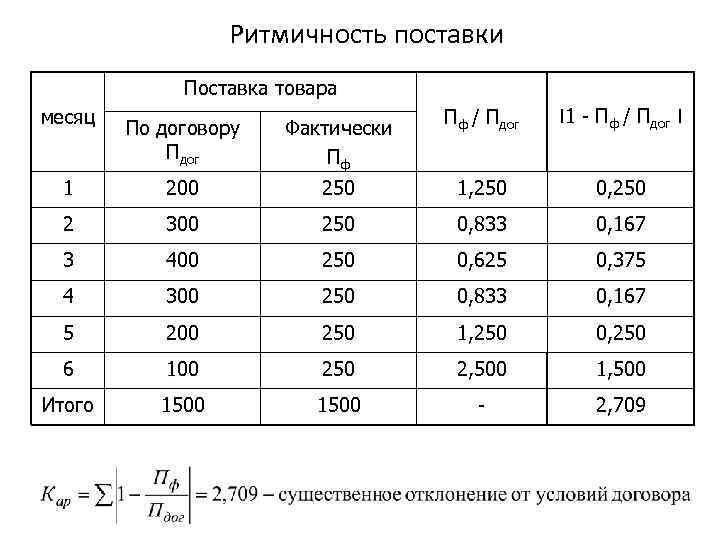Ритмичность поставки Поставка товара Пф / Пдог І1 - Пф / Пдог І 250 1, 250 0, 250 300 250 0, 833 0, 167 3 400 250 0, 625 0, 375 4 300 250 0, 833 0, 167 5 200 250 1, 250 0, 250 6 100 250 2, 500 1, 500 Итого 1500 - 2, 709 месяц По договору Пдог Фактически Пф 1 200 2

Индексы это относительные величины, характеризующие изменение единицы совокупности, группы единиц или всей совокупности в целом во времени или в пространстве по сравнению с нормативами (планом, прогнозом, нормативом). Необходимость введения индексов связана с тем, что обычно сопоставляемые показатели характеризуют явления, состоящие из однородных элементов, суммирование которых невозможно в силу их несоизмеримости

Типы индексов • Динамические: применяются для анализа динамики явления. В зависимости от базы сравнения индексы могут быть базисными или цепными. Они показывают во сколько раз или на сколько процентов (индекс*100 -100) или на сколько единиц (разность между числителем и знаменателем индекса) вырос или уменьшился показатель, характеризующий явление. Базисный период принято считать 0, текущий (отчетный) -1. • Территориальные: характеризуют изменение в пространстве. Они служат для сравнительной оценки явления по территориям и показывают во сколько раз или на сколько процентов или на сколько единиц величина явления на одной территории больше или меньше чем на другой. • Нормативные: обеспечивают сравнение с нормативами. Они предназначены для анализа выполнения плана, договоров, нормативов и показывают процент перевыполнения или недовыполнения плана, договора.

Свойства индексов • Синтетические: показывают изменение изучаемого показателя в среднем; • Аналитические: позволяют выявить влияние индексируемого показателя на результативную величину.

Задачи, решаемые с помощью индексов: оценка динамики показателей, характеризующих разнородные совокупности; • анализ влияния факторов на изменение результативных показателей; • территориальные сравнения; • оценка выполнения плана, договора; • факторный анализ выполнения плана, договора.

При построении индексов все показатели делятся на: • Качественные рассчитываются на единицу чеголибо (цена, себестоимость, производительность труда, урожайность). • Количественные выражают объем явления, они подлежат суммированию (физический объем произведенной продукции, численность работников, размер площади). • Обобщающие характеризуют изменение явления в целом.

По степени охвата единиц совокупности индексы делятся на два класса: индивидуальные и общие. • Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. • Общий индекс отражает изменение всех элементов сложного явления, отдельные элементы которого не подлежат суммированию.

Алгоритм расчета индивидуальных индексов • • • Индивидуальный индекс обозначается буквой i со знаком индексируемого показателя. Например, индивидуальный индекс цены записывается ip, физического объема – iq. Индекс – относительная величина, поэтому всегда представлен дробью. В числителе индекса записывается значение индексируемого показателя в отчетном периоде (p 1, q 1), а в знаменателе – значение базисного показателя (p 0, q 0).

Между индексами количественных, качественных и стоимостных показателей существует та же взаимосвязь, что и между индексируемыми показателями. Товарооборот – это произведение цены на количество проданных товаров, значит общий индекс товарооборота равен произведению индексов цены и физического объема: (мультипликативная модель). Общее абсолютное изменение товарооборота за счет цены и количества проданных товаров равно сумме абсолютных изменений товарооборота за счет каждого фактора в отдельности: (аддитивная модель).

Проанализируем изменение продажи товара А, если цена на него выросла с 25 рублей до 30, а объем продаж снизился с 3 тыс. шт. до 2, 7. В целом стоимость проданного товара в текущем периоде по сравнению с базисным увеличилась на 8% или 6 тыс. руб. , в том числе за счет: • роста цен на товар на 20% или 5 рублей стоимость проданного товара увеличилась на 13. 5 тыс. руб. ; • снижения объема реализации на 10% или 0, 3 тыс. шт. стоимость проданного товара уменьшилась на 7. 5 тыс. руб.

Способы построения общих индексов 1. Агрегатные 2. Средние арифметические или гармонические из индивидуальных

Алгоритм расчета агрегатных индексов • Агрегатный индекс обозначается буквой I со знаком индексируемой величины. • Это дробь, в числителе и знаменателе которой сумма произведений. • Первый сомножитель - индексируемая величина. Она изменяется: в числителе из отчетного периода (1), в знаменателе – из базисного (0). • Второй сомножитель – вес или соизмеритель остается без изменения (в числителе и знаменателе одинаков). • Если индексируется количественный показатель, то весом является качественный показатель базисного периода. Если индексируется качественный показатель, то весом является количественный показатель отчетного периода. • Индексы с весами базисного периода являются индексами, построенными по методике Ласпейреса. Индексы с весами отчетного периода являются индексами, построенными по методике Пааше.

Введем обозначения: Тогда агрегатный индекс физического объема : Агрегатный индекс цен : Агрегатный индекс товарооборота (стоимости продукции) в фактических ценах:

Агрегатный индекс физического объема продаж Ласпейреса • показывает во сколько раз или на сколько процентов увеличилось (уменьшилось) в среднем количество проданных товаров отчетном периоде по сравнению с базисным периодом. • Разность между числителем и знаменателем агрегатного индекса физического объема характеризует абсолютное изменение товарооборота (прирост или снижение) за счет происшедшего изменения количества проданных товаров:

Агрегатный индекс цен Пааше • показывает во сколько раз или на сколько процентов увеличилась (уменьшилась) в среднем цена проданных товаров отчетном периоде по сравнению с базисным периодом. • Разность между числителем и знаменателем агрегатного индекса цены характеризует абсолютное изменение товарооборота (прирост или снижение) за счет происшедшего изменения цен на проданные товары:

Агрегатный индекс товарооборота • показывает во сколько раз возрос (уменьшился) товарооборот отчетного периода по сравнению с базисным или сколько процентов составляет рост (снижение) товарооборота. Если из значения индекса вычесть 100% , то разность покажет на сколько процентов вырос (уменьшился) товарооборот в отчетном периоде по сравнению с базисным за счет изменения цен и количества проданных товаров (относительное изменение). • Разность числителя и знаменателя этого индекса показывает на сколько денежных единиц увеличился (уменьшился) товарооборот в текущем периоде по сравнению с базисным за счет изменения двух факторов: цен и количества проданных товаров (абсолютное изменение).

Взаимосвязь агрегатных индексов • Мультипликативная модель • Аддитивная модель

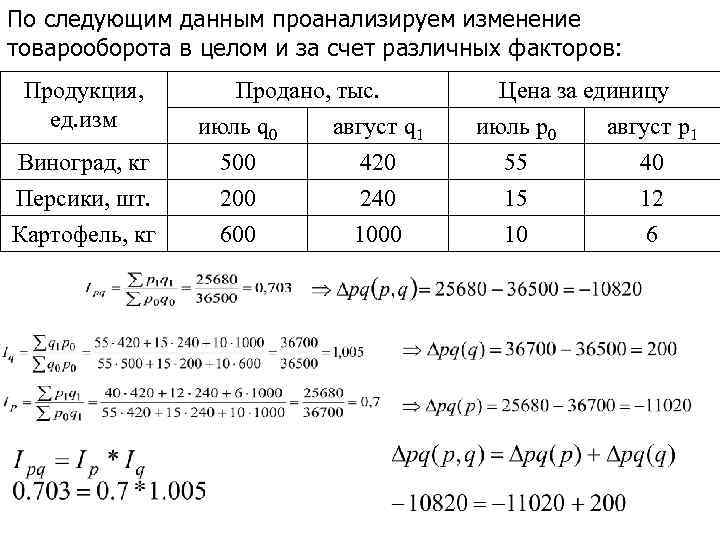По следующим данным проанализируем изменение товарооборота в целом и за счет различных факторов: Продукция, ед. изм Виноград, кг Персики, шт. Картофель, кг Продано, тыс. июль q 0 август q 1 500 420 200 240 600 1000 Цена за единицу июль p 0 август p 1 55 40 15 12 10 6

Выводы: В целом стоимость проданных фруктов в августе по сравнению с июлем уменьшилась на 70, 3 -100=29, 7% или 10820 тыс. руб. , в том числе за счет: • снижения цен на фрукты в среднем на 30% товарооборот проданных товаров уменьшился на 11020 тыс. руб. ; • роста объема реализации в среднем на 0, 5% товарооборот проданных товаров увеличился на 200 тыс. руб.

Формулы расчета среднеарифметического и среднегармонического индекса цен и физического объема: Среднеарифметический индекс Общий индекс физического объема Общий индекс цен Среднегармонический индекс

Выбор формы среднего индекса зависит от исходных данных. • Среднеарифметический индекс физического объема удобно применять в тех случаях, когда известны изменение количества проданных товаров (iq) и товарооборот базисного периода. • При наличии данных об изменении цен на отдельные товары (ip) и фактического товарооборота базисного периода используется среднегармонический индекс цен.

По следующим данным охарактеризовать изменение производства продукции. Вид продукции Выпуск продукции в I кв, млн. руб. Изменение объема производства во IIкв. в натуральном выражении, % Пленка 30 +10 Пеноплен Линолеум 25 40 -10 -25 Снижение объема производства в среднем на 10% повлекло снижение стоимости произведенной продукции на 85, 5 – 95 = 9, 5 млн. руб.

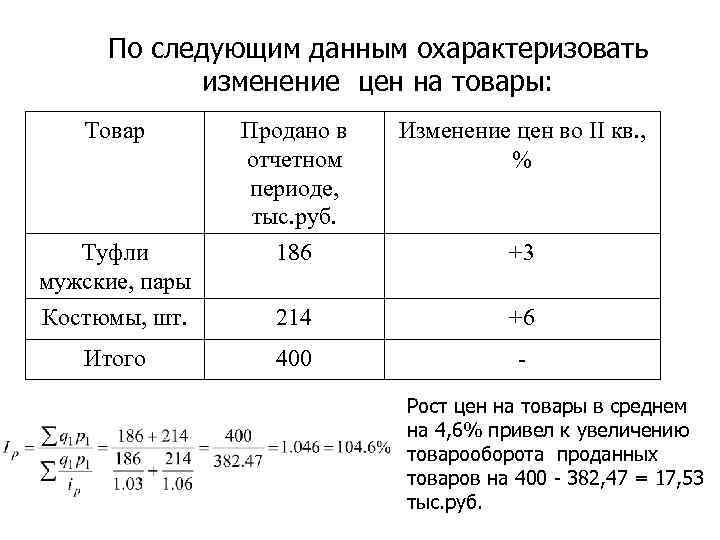По следующим данным охарактеризовать изменение цен на товары: Товар Продано в отчетном периоде, тыс. руб. 186 Изменение цен во II кв. , % Костюмы, шт. 214 +6 Итого 400 - Туфли мужские, пары +3 Рост цен на товары в среднем на 4, 6% привел к увеличению товарооборота проданных товаров на 400 - 382, 47 = 17, 53 тыс. руб.

Цепные и базисные индексы Для проведения анализа динамики явления за интервал времени, включающий более двух периодов строят ряд индексов, которые образуют индексные системы. • Ряд индексов, каждый из которых рассчитан по отношению к базисному (первоначальному) периоду, именуют базисным. • Ряд индексов, каждый из которых рассчитан по отношению к предыдущему периоду, именуют цепным.

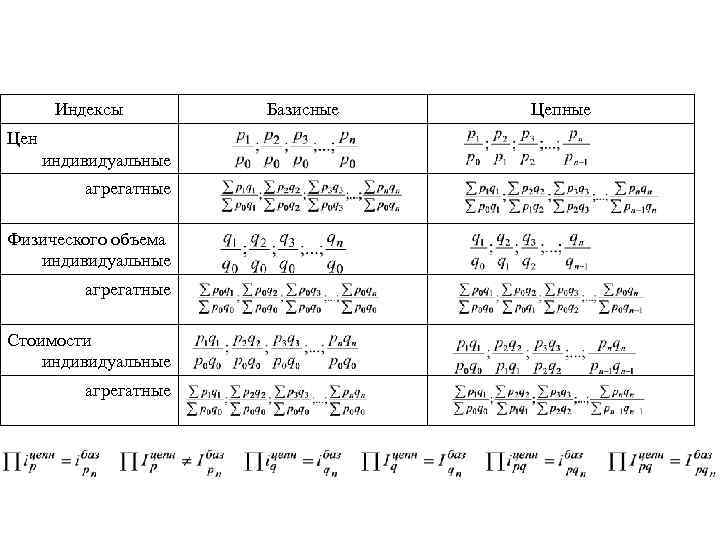Система базисных и цепных индексов цен, физического объема и стоимости продукции: Индексы Цен индивидуальные агрегатные Физического объема индивидуальные агрегатные Стоимости индивидуальные агрегатные Базисные Цепные