Ряды динамики План 1 Ряды динамики их виды

Ряды динамики План 1. Ряды динамики, их виды. 2. Аналитические показатели ряда динамики 3. Средние показатели в рядах динамики 4. Сопоставимость уровней и смыкание рядов динамики. 5. Методы анализа основной тенденции в рядах динамики 6. Статистическое изучение сезонных колебаний 7. Экстраполяция и прогнозирование в рядах динамики

1. Ряды динамики, их виды. Процесс социально-экономического развития во времени называется динамикой. Для отображения динамики развития строят ряды динамики – это хронологические, т. е. временные ряды. Ряд динамики представляют собой последовательность изменяющихся во времени значений статистического показателя. Составными элементами ряда является: время t (годы, мес, . . моменты, т. е. даты) и конкретное значение показателя y, которое принято называть уровнем ряда.

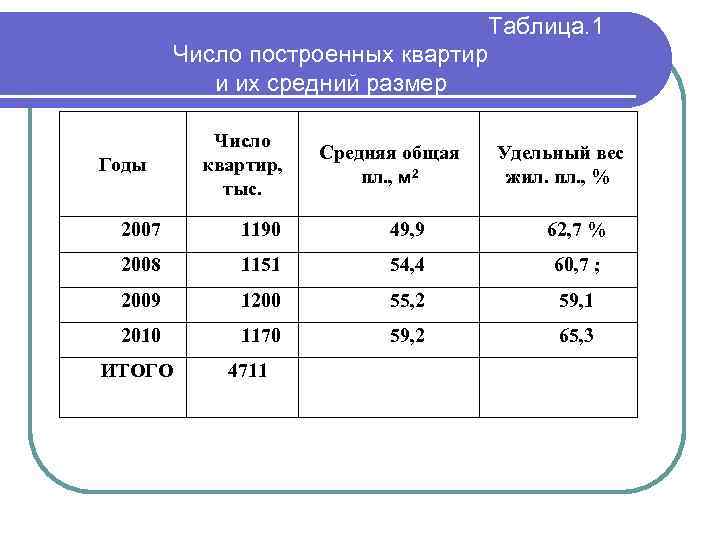Таблица. 1 Число построенных квартир и их средний размер Годы Число квартир, тыс. Средняя общая пл. , м 2 Удельный вес жил. пл. , % 2007 1190 49, 9 62, 7 % 2008 1151 54, 4 60, 7 ; 2009 1200 55, 2 59, 1 2010 1170 59, 2 65, 3 ИТОГО 4711

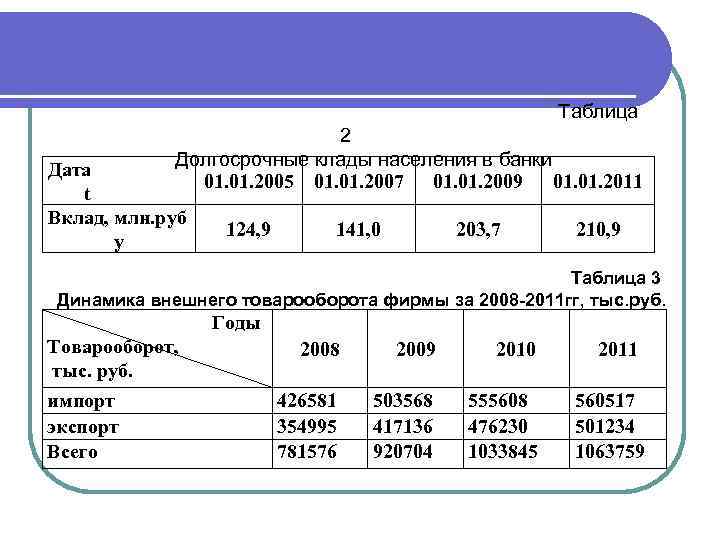Таблица 2 Долгосрочные клады населения в банки Дата 01. 2005 01. 2007 01. 2009 01. 2011 t Вклад, млн. руб 124, 9 141, 0 203, 7 210, 9 y Таблица 3 Динамика внешнего товарооборота фирмы за 2008 -2011 гг, тыс. руб. Годы Товарооборот, тыс. руб. импорт экспорт Всего 2008 2009 2010 426581 354995 781576 503568 417136 920704 555608 476230 1033845 2011 560517 501234 1063759

2. Аналитические показатели ряда динамики 1. l Абсолютные показатели динамики: абсолютные приросты 2. Относительные показатели динамики l темпы роста - базисные - цепные l абсолютное значение 1 -го процента прироста абс. 1% l темпы прироста

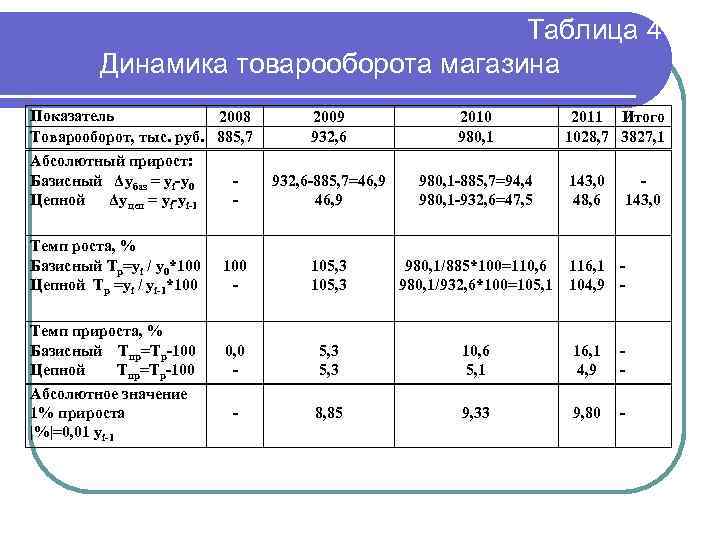. Таблица 4 Динамика товарооборота магазина Показатель 2008 Товарооборот, тыс. руб. 885, 7 2009 932, 6 2010 980, 1 -885, 7=94, 4 980, 1 -932, 6=47, 5 2011 Итого 1028, 7 3827, 1 Абсолютный прирост: Базисный Δубаз = yi-y 0 Цепной Δуцеп = yi-yi-1 - 932, 6 -885, 7=46, 9 Темп роста, % Базисный Тр=yi / y 0*100 Цепной Тр =yi / yi-1*100 - 105, 3 0, 0 - 5, 3 10, 6 5, 1 16, 1 4, 9 - - 8, 85 9, 33 9, 80 - Темп прироста, % Базисный Тпр=Тр-100 Цепной Тпр=Тр-100 Абсолютное значение 1% прироста |%|=0, 01 yi-1 143, 0 48, 6 143, 0 980, 1/885*100=110, 6 116, 1 980, 1/932, 6*100=105, 1 104, 9 -

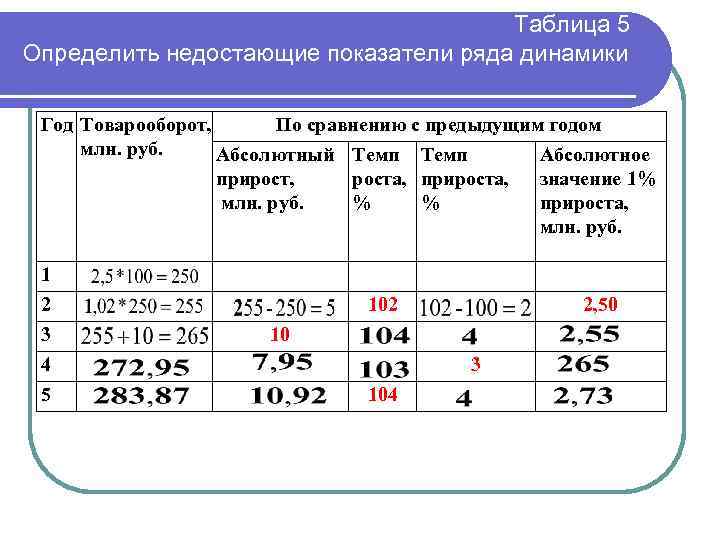Таблица 5 Определить недостающие показатели ряда динамики Год Товарооборот, По сравнению с предыдущим годом млн. руб. Абсолютный Темп Абсолютное прирост, млн. руб. роста, прироста, % % значение 1% прироста, млн. руб. 1 2 3 102 10 4 5 2, 50 3 104

3. Средние показатели в рядах динамики В интервальных: В моментных: l с равными интервалами l с одинаковыми промежутками времени между моментами l с неравными интервалами l с неодинаковыми промежутками времени

Примеры. Для примера 4 среднегодовой товарооборот магазина: Пример 6. Известны товарные остатки магазина на 1 число каждого месяца, тыс. руб. : 01. 01 01. 02 01. 03 01. 04 18 14 16 20 Среднемесячный товарный остаток за квартал составит:

Примеры. Пример 7. Известна списочная численность рабочих организации, чел. 01. 10 01. 03. 10 01. 04. 10 01. 09. 10 1. 01. 11 1200 1100 1250 1500 1350 Среднегодовая численность рабочих за 2010 год составит:

Средние из характеристик динамического ряда 1. Средний абсолютный прирост 2. Средний темп роста на основе цепных абсолютных приростов на основе базисного абсолютного прироста m=n– 1 3. Средний темп прироста

Для примера 4: Средний абсолютный прирост составит: Средний темп роста товарооборота за 2008 -2011 гг. составит: Средний темп прироста составит:

4. Сопоставимости в рядах динамики Важнейшим условием при построении ряда динамики является сопоставимость всех входящих в него уровней. Это условие соблюдается либо в процессе сбора и обработки данных, либо путем пересчета уровней. Основные причины несопоставимости уровней динамики: 1. Изменение единиц измерения или единиц счета (ткань в погонных метрах или в квадратных метрах). 2. Различные методологии учета или расчета показателей. 3. Наличие неравных интервалов при интервальном ряде. 4. Изменение территориальных границ

При отсутствии сопоставимости нужно, пользуясь дополнительными расчетами, привести ряды к сопоставимому виду. Для этого используется приём «смыкание рядов динамики» , т. е. Объединение в один ряд двух или нескольких рядов, уровни которых исчислены по разной методологии или в разных территориальных границах. Чтобы произвести смыкание, нужно наличие переходного периода, для которого имеются данные исчисленные по разной методологии или в разных территориальных границах. .

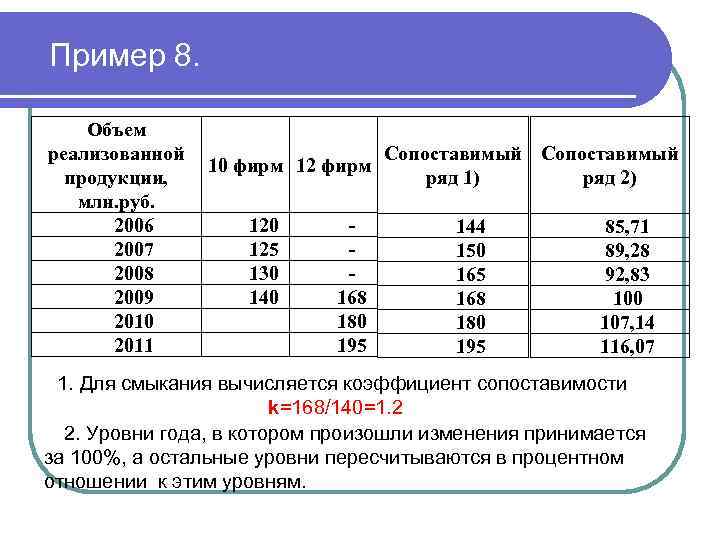Пример 8. Объем реализованной продукции, млн. руб. 2006 2007 2008 2009 2010 2011 10 фирм 120 125 130 140 168 180 195 Сопоставимый ряд 1) ряд 2) 144 150 165 168 180 195 85, 71 89, 28 92, 83 100 107, 14 116, 07 1. Для смыкания вычисляется коэффициент сопоставимости k=168/140=1. 2 2. Уровни года, в котором произошли изменения принимается за 100%, а остальные уровни пересчитываются в процентном отношении к этим уровням.

8. Методы анализа основной тенденции в рядах динамики На развитие явления во времени оказывают влияние различные факторы. Тенденция развития явления определяется основным фактором, однако, кроме основного фактора на развитие явления оказывает влияние (прямое или косвенное) множество других факторов (случайных, разовых, периодических). Поэтому речь идет не просто о тенденции развития, а об основной тенденции развития, достаточно стабильной на протяжении изучаемого этапа развития. Часто бывают такие ряды динамики, в которых уровни претерпевают самые различные изменения, тогда общая тенденция развития неясна.

Основной тенденции развития (трендом) называется устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Для того, чтобы выявить тенденцию развития изучаемого явления, необходимо иметь данные за длительный период времени. Используют три метода: 1. Метод укрупнения интервалов. 2. Метод скользящей средней. 3. Метод аналитического выравнивания. Первый метод – укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики. При этом уменьшается количество интервалов. Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер основной тенденции развития.

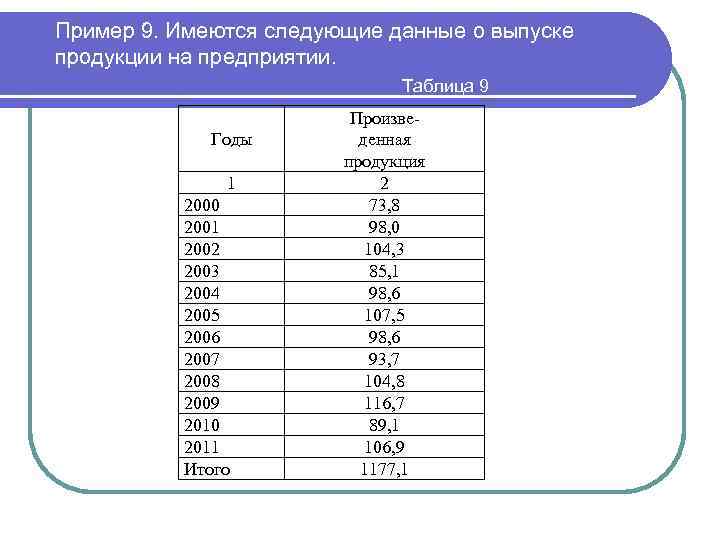Пример 9. Имеются следующие данные о выпуске продукции на предприятии. Таблица 9 Годы 1 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 Итого Произведенная продукция 2 73, 8 98, 0 104, 3 85, 1 98, 6 107, 5 98, 6 93, 7 104, 8 116, 7 89, 1 106, 9 1177, 1

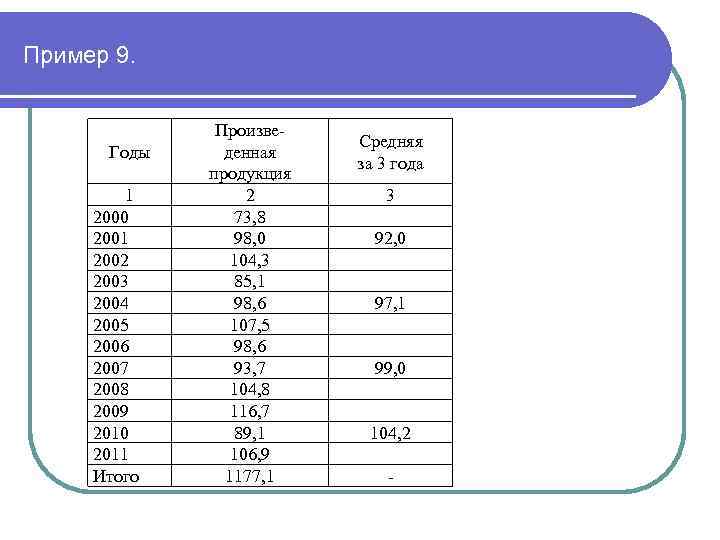Пример 9. Годы 1 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 Итого Произведенная продукция 2 73, 8 98, 0 104, 3 85, 1 98, 6 107, 5 98, 6 93, 7 104, 8 116, 7 89, 1 106, 9 1177, 1 Средняя за 3 года 3 92, 0 97, 1 99, 0 104, 2 -

Второй метод - метод скользящей средней также основан на исчислении средних величин за укрупненные периоды времени (идея та же – устранить влияние случайных факторов путем их взаимопогашения за отдельные годы). Однако метод расчета другой: - исчисляются 3 -х или 5 -ти летние средние, которые скользят по годам, образуя различные 3 -х и 5 -ти летние периоды; По формуле простой средней арифметической отыскиваются средние значения и записываются напротив среднего года. Сглаженный ряд по пятилетиям короче фактического на 4 члена ряда ( 2 в начале и 2 в конце). Он меньше, чем фактический ряд подвержен колебаниям из-за случайных причин и четче выражает основную тенденцию роста выпускаемой продукции. Недостаток – «укорачивание» ряда, а, следовательно, и потеря информации.

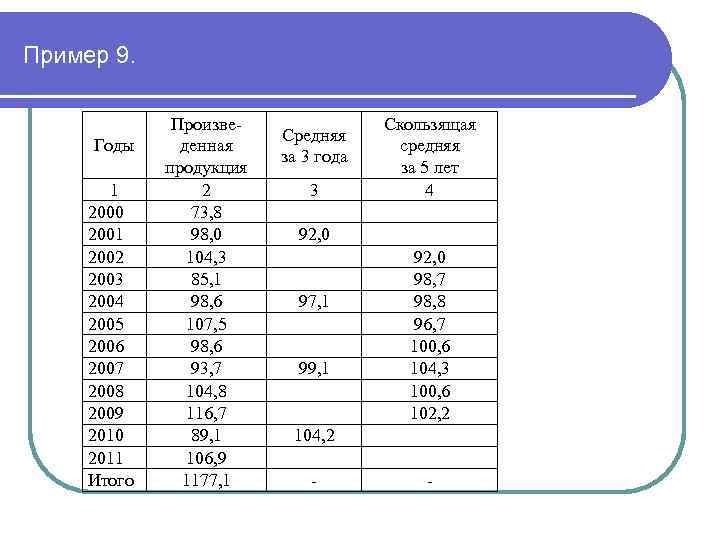Пример 9. Годы 1 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 Итого Произведенная продукция 2 73, 8 98, 0 104, 3 85, 1 98, 6 107, 5 98, 6 93, 7 104, 8 116, 7 89, 1 106, 9 1177, 1 Средняя за 3 года 3 Скользящая средняя за 5 лет 4 92, 0 97, 1 99, 1 92, 0 98, 7 98, 8 96, 7 100, 6 104, 3 100, 6 102, 2 104, 2 - -

Рассмотренные два метода дают возможность определить лишь общую тенденцию развития, Однако получить обобщенную статистическую модель тренда по этим методам невозможно. Для того, чтобы дать количественную модель, используется аналитическое выравнивание ряда динамики. Третий метод – метод аналитического выравнивания заключается в нахождении аналитического уравнения , описывающего тенденцию развития во времени. Для этого используют метод аналогичный регрессионному методу: 1) строиться система нормальных уравнений, 2) определяются числовые значения коэффициентов аналитического уравнения.

На основе найденного уравнения тренда вычисляются выровненные уровни ряда. Выравнивание ряда динамики заключается в замене фактических уровней уi плавно изменяющимися уровнями , наилучшим образом аппроксимирующими статистические данные. Рассмотрим применение метода на примере уравнения прямой линии: Для определения параметров методом регрессионного анализа с использованием методов наименьших квадратов, строим систему нормальных уравнений:

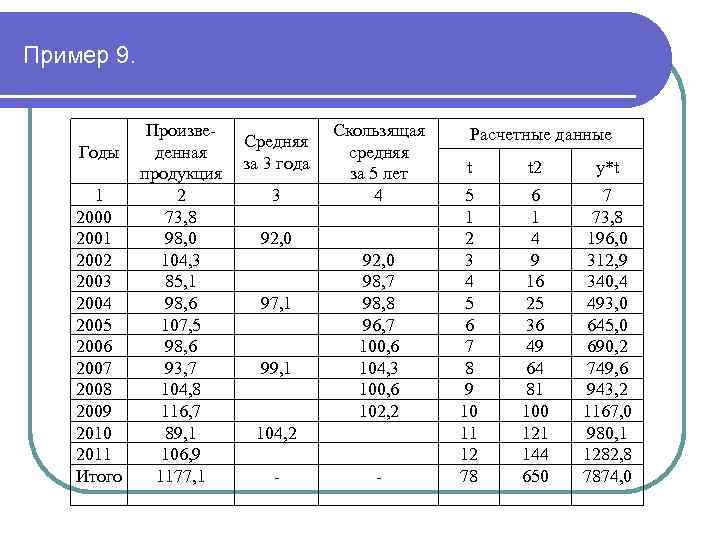Пример 9. Произведенная Годы продукция 1 2 2000 73, 8 2001 98, 0 2002 104, 3 2003 85, 1 2004 98, 6 2005 107, 5 2006 98, 6 2007 93, 7 2008 104, 8 2009 116, 7 2010 89, 1 2011 106, 9 Итого 1177, 1 Средняя за 3 года 3 Скользящая средняя за 5 лет 4 92, 0 97, 1 99, 1 92, 0 98, 7 98, 8 96, 7 100, 6 104, 3 100, 6 102, 2 104, 2 - - Расчетные данные t t 2 у*t 5 1 2 3 4 5 6 7 8 9 10 11 12 78 6 1 4 9 16 25 36 49 64 81 100 121 144 650 7 73, 8 196, 0 312, 9 340, 4 493, 0 645, 0 690, 2 749, 6 943, 2 1167, 0 980, 1 1282, 8 7874, 0

Расчетные показатели приведены в табл. 9 графы 5 -7. Вычислим по данной формуле значения и запишем их в графу 8 табл. 9 В выровненном ряду происходит равномерное возрастание уровня ряда в среднем за год на 1, 555 млн. тонн. На это указывает коэффициент регрессии 1, 555. Равномерность возрастания связана с тем, моделирование проводиться по уравнению прямой и коэффициент при t (коэффициент регрессии) положительный.

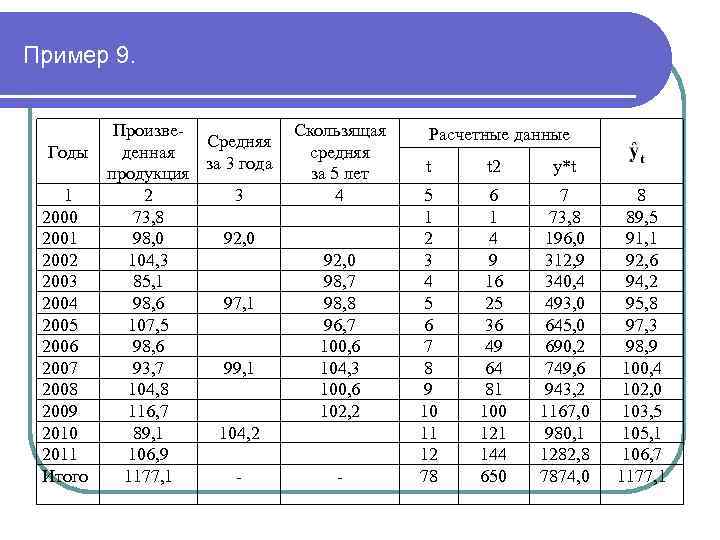Пример 9. Годы 1 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 Итого Произве. Средняя денная за 3 года продукция 2 3 73, 8 98, 0 92, 0 104, 3 85, 1 98, 6 97, 1 107, 5 98, 6 93, 7 99, 1 104, 8 116, 7 89, 1 104, 2 106, 9 1177, 1 - Скользящая средняя за 5 лет 4 92, 0 98, 7 98, 8 96, 7 100, 6 104, 3 100, 6 102, 2 - Расчетные данные t t 2 у*t 5 1 2 3 4 5 6 7 8 9 10 11 12 78 6 1 4 9 16 25 36 49 64 81 100 121 144 650 7 73, 8 196, 0 312, 9 340, 4 493, 0 645, 0 690, 2 749, 6 943, 2 1167, 0 980, 1 1282, 8 7874, 0 8 89, 5 91, 1 92, 6 94, 2 95, 8 97, 3 98, 9 100, 4 102, 0 103, 5 105, 1 106, 7 1177, 1

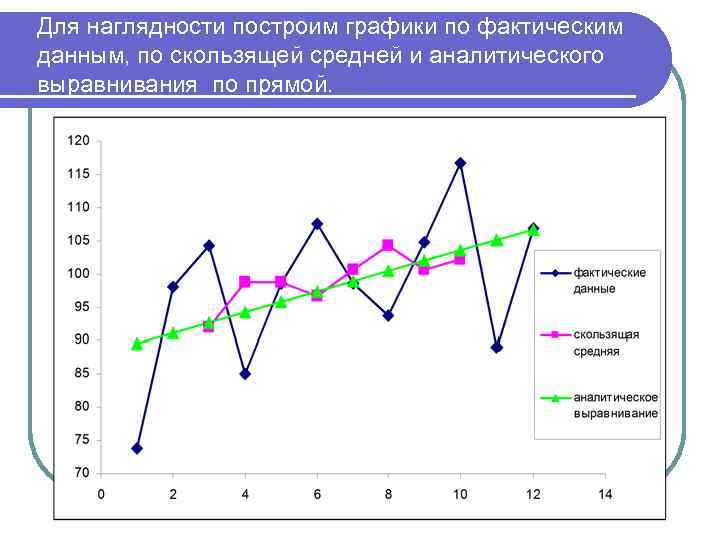Для наглядности построим графики по фактическим данным, по скользящей средней и аналитического выравнивания по прямой.

6. Статистическое изучение сезонных колебаний Изучение сезонных колебаний производится с целью выявления закономерных повторений различий в уровнях ряда динамики в зависимости от времени года. Для того, чтобы выявление сезонных различий были не случайными, а закономерными, анализ строится на данных нескольких лет (не менее 3 х). Для изучение сезонных колебаний определяется показатель сезонной волны – индекс сезонности в %: Здесь: - средний уровень для каждого месяца; - среднемесячный уровень для всего ряда. Для наглядного представления сезонной волны исчисленные индексы сезонности изображают в виде графика.

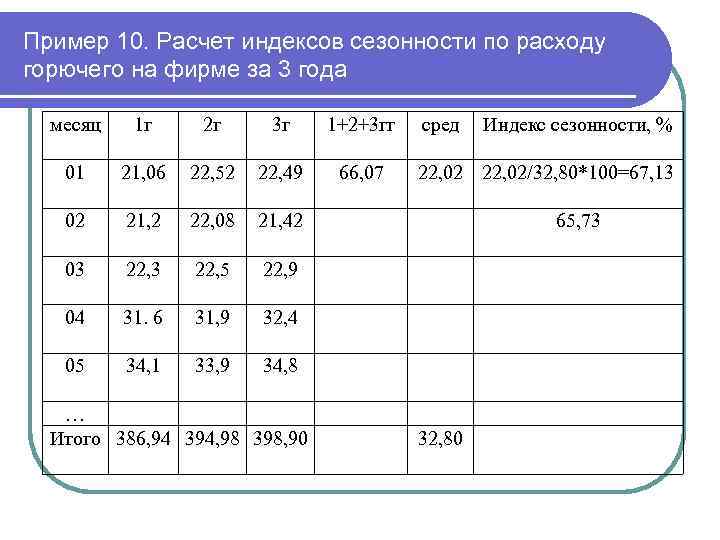Пример 10. Расчет индексов сезонности по расходу горючего на фирме за 3 года месяц 1 г 2 г 3 г 1+2+3 гг 01 21, 06 22, 52 22, 49 66, 07 02 21, 2 22, 08 21, 42 03 22, 5 22, 9 04 31. 6 31, 9 32, 4 05 34, 1 33, 9 34, 8 … Итого 386, 94 394, 98 398, 90 сред Индекс сезонности, % 22, 02/32, 80*100=67, 13 65, 73 32, 80

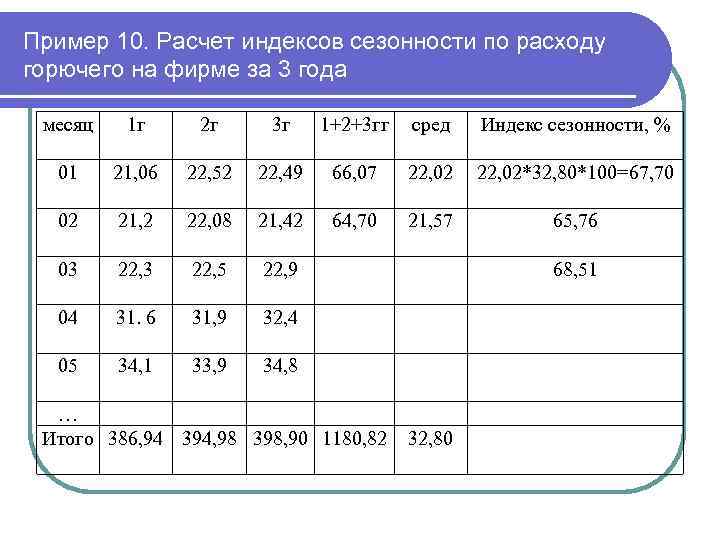Пример 10. Расчет индексов сезонности по расходу горючего на фирме за 3 года месяц 1 г 2 г 3 г 1+2+3 гг сред Индекс сезонности, % 01 21, 06 22, 52 22, 49 66, 07 22, 02*32, 80*100=67, 70 02 21, 2 22, 08 21, 42 64, 70 21, 57 65, 76 03 22, 5 22, 9 04 31. 6 31, 9 32, 4 05 34, 1 33, 9 34, 8 … Итого 386, 94 394, 98 398, 90 1180, 82 68, 51 32, 80

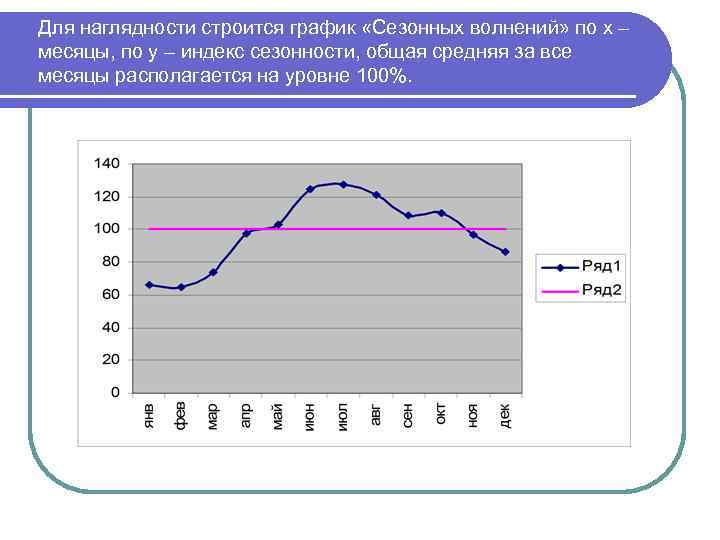Для наглядности строится график «Сезонных волнений» по х – месяцы, по у – индекс сезонности, общая средняя за все месяцы располагается на уровне 100%.

7. Экстраполяция и прогнозирование в рядах динамики Необходимым условием рыночных регулирования отношений является составление надежных прогнозов развития социально-экономических явлений. Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования. Для этого используют метод экстраполяции, т. е. нахождение уровней за пределами изучаемого ряда. Так как в действительности тренд не остается неизменным, то данные экстраполяции нужно рассматривать как вероятностные оценки. Для экстраполяции применяют различные способы. Экстраполяцию выполняют на основе: • Среднего абсолютного прироста. • Среднего темпа роста. • Выравнивания рядов по аналитическим формулам.

Прогнозирование по среднему абсолютному приросту может быть выполнено, если есть уверенность считать общую тенденцию линейной, т. е. метод основан на предположении о равномерном изменении уровня. Тогда средний абсолютный прирост последовательно прибавляется к последнему уровню yn столько раз, на сколько периодов экстраполируется ряд: Средний абсолютный прирост для примера 9 :

Тогда Прогнозирование по среднему абсолютному приросту может быть выполнено, если есть уверенность считать общую тенденцию нелинейной – показательной: Чаще всего используют третий метод - выравнивание рядов по аналитическим формулам. Рассмотрим этот метод по данным примера 9 о выпуске продукции на предприятии на основе полученного уравнения

Экстраполяцией при t =14 можно получить ожидаемый выпуск продукции в 2013 г. : =87, 96 + 1, 555*14=87, 96+21, 77=109, 73 млн. т. Для определения границ доверительного интервала используют формулу где - коэффициент доверия Стьюдента; - остаточное среднеквадратическое отклонение от тренда, скорректированное по числу степеней свободы (n-m); n – число уровней ряда динамики; m – число параметров адекватной модели тренда ( для уравнения примой m=2, т. е. а 0 и а 1).

Вероятностные границы интервала прогнозируемого явления: Рассчитаем прогнозируемые доверительные интервалы выпуска продукции на 2013 г. При n=12 и m =2 число степеней свободы равно 10. Тогда при доверительной вероятности 0, 95 ( т. е. α =0, 05) коэффициент доверия по таблице Стьюдента tα=2, 228. Для примера 9 Определим вероятностные границы: 86, 27≤ упр ≤ 133, 19