Ручная локация сейсмических событий Асминг В Э Презентация

Ручная локация сейсмических событий Асминг В. Э. Презентация для семинара в Алматы август 2014

Содержание • Методы засечек и их реализация в EL_WIN • Минимизация невязок времени в очаге • Определение глубин • Ошибки локации, их виды • Локация событий в неоднородных средах • Регионализация по Бондарю (Wave. Eater) • Локация на графе (Seismo. Configurator)

Классический метод засечек Если известны времена приходов P и S-волн на одну станцию, можно нарисовать линию, откуда пришел сигнал (при фиксированной глубине). Эта линия – окружность для одномерной среды. Для неоднородной среды может иметь более сложную форму. Будем дальше называть их «линии P-S» . Пересечение этих линий (окружностей), построенных по нескольким станциям, дает локацию сейсмического события Реализация метода в EL_WIN

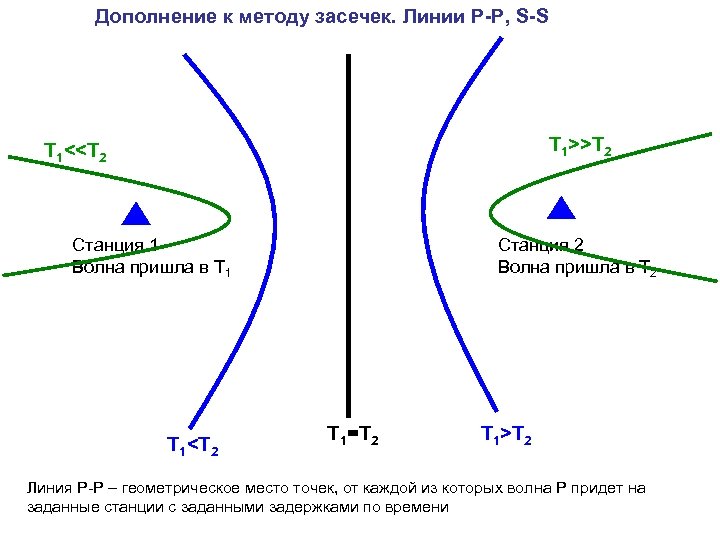
Дополнение к методу засечек. Линии P-P, S-S T 1>>T 2 T 1<<T 2 Станция 1 Волна пришла в T 1<T 2 Станция 2 Волна пришла в T 2 T 1=T 2 T 1>T 2 Линия P-P – геометрическое место точек, от каждой из которых волна P придет на заданные станции с заданными задержками по времени

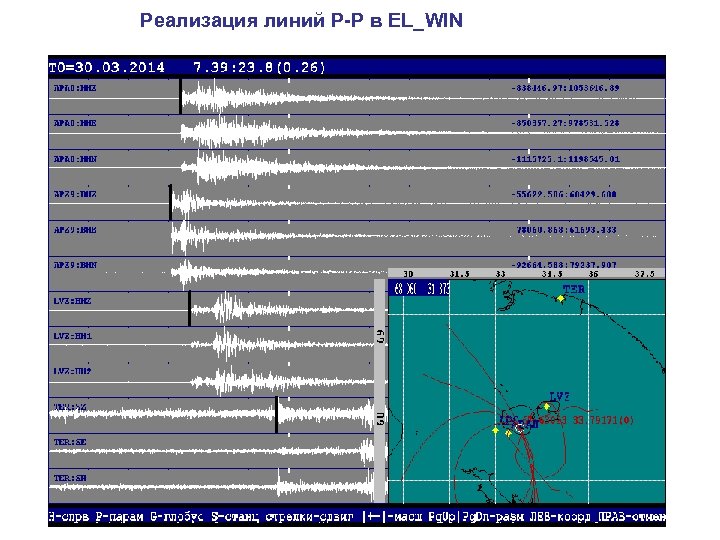
Реализация линий P-P в EL_WIN

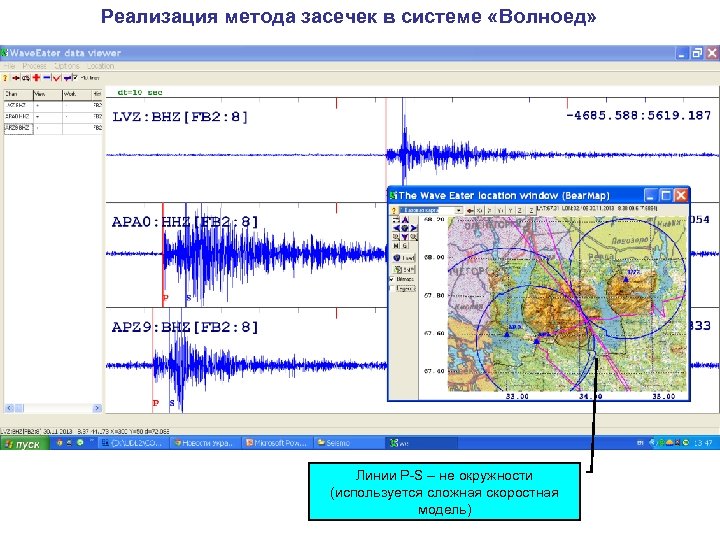
Реализация метода засечек в системе «Волноед» Линии P-S – не окружности (используется сложная скоростная модель)

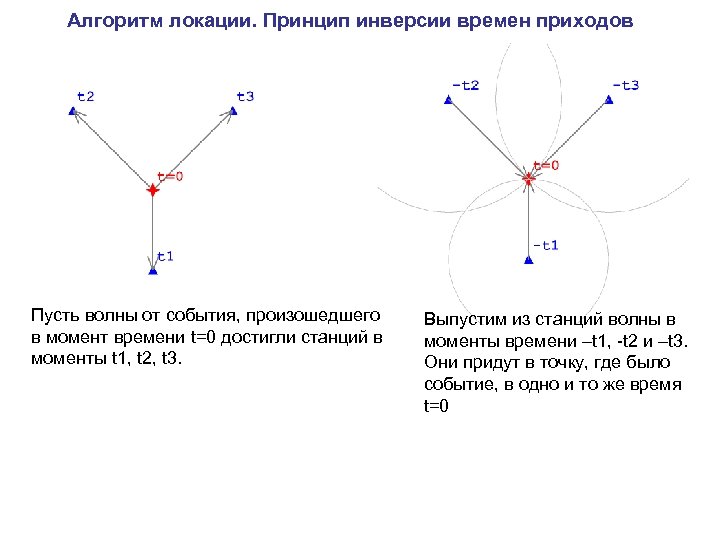
Алгоритм локации. Принцип инверсии времен приходов Пусть волны от события, произошедшего в момент времени t=0 достигли станций в моменты t 1, t 2, t 3. Выпустим из станций волны в моменты времени –t 1, -t 2 и –t 3. Они придут в точку, где было событие, в одно и то же время t=0

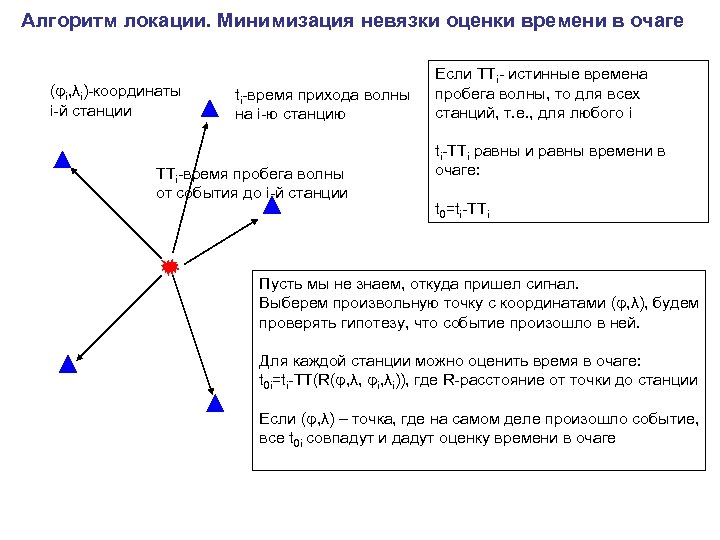
Алгоритм локации. Минимизация невязки оценки времени в очаге (φi, λi)-координаты i-й станции ti-время прихода волны на i-ю станцию TTi-время пробега волны от события до i-й станции Если TTi- истинные времена пробега волны, то для всех станций, т. е. , для любого i ti-TTi равны и равны времени в очаге: t 0=ti-TTi Пусть мы не знаем, откуда пришел сигнал. Выберем произвольную точку с координатами (φ, λ), будем проверять гипотезу, что событие произошло в ней. Для каждой станции можно оценить время в очаге: t 0 i=ti-TT(R(φ, λ, φi, λi)), где R-расстояние от точки до станции Если (φ, λ) – точка, где на самом деле произошло событие, все t 0 i совпадут и дадут оценку времени в очаге

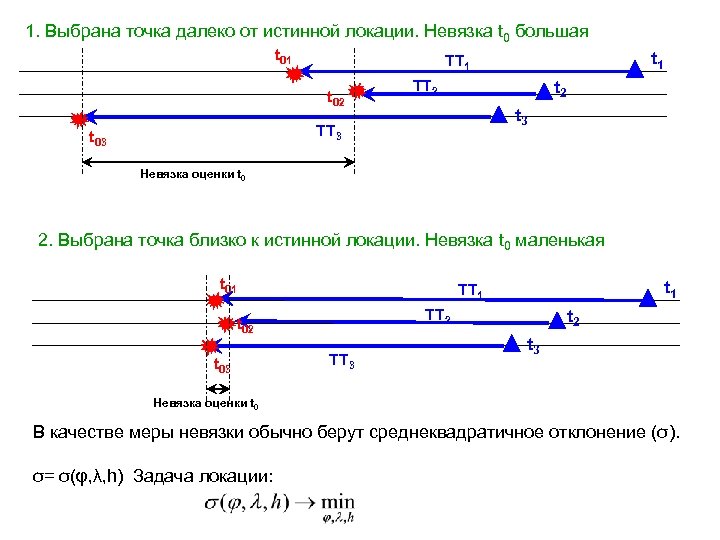
1. Выбрана точка далеко от истинной локации. Невязка t 0 большая t 01 t 02 TT 2 t 3 TT 3 t 03 t 1 TT 1 Невязка оценки t 0 2. Выбрана точка близко к истинной локации. Невязка t 0 маленькая t 01 TT 2 t 03 t 1 TT 3 t 2 t 3 Невязка оценки t 0 В качестве меры невязки обычно берут среднеквадратичное отклонение (σ). σ= σ(φ, λ, h) Задача локации:

Решение задачи может быть выполнено разными способами (см. теорию оптимизации) В общем случае функция σ(φ, λ, h) может быть овражной, может иметь локальные минимумы В программе EL_WIN реализована градиентная минимизация (начальную точку указывает пользователь) В программе «Волноед» реализована произвольная (задаваемая пользователем) комбинация поиска из начальной точки с постоянными шагами и поиска по сетке, охватывающей область локации, с ее последовательным уменьшением

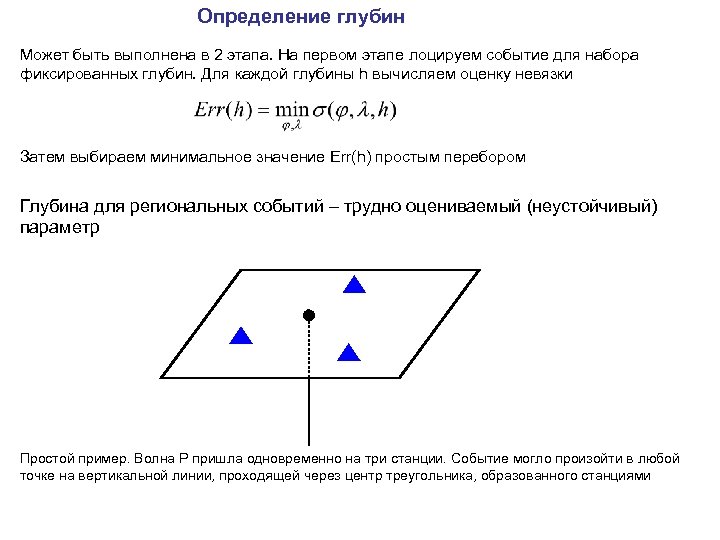
Определение глубин Может быть выполнена в 2 этапа. На первом этапе лоцируем событие для набора фиксированных глубин. Для каждой глубины h вычисляем оценку невязки Затем выбираем минимальное значение Err(h) простым перебором Глубина для региональных событий – трудно оцениваемый (неустойчивый) параметр Простой пример. Волна P пришла одновременно на три станции. Событие могло произойти в любой точке на вертикальной линии, проходящей через центр треугольника, образованного станциями

Пример. Локация события системой «Волноед» Поиск из заданной пользователем точки Стартовая точка, заданная пользователем Путь из стартовой точки в точку локации Зависимость невязки времени в очаге от глубины

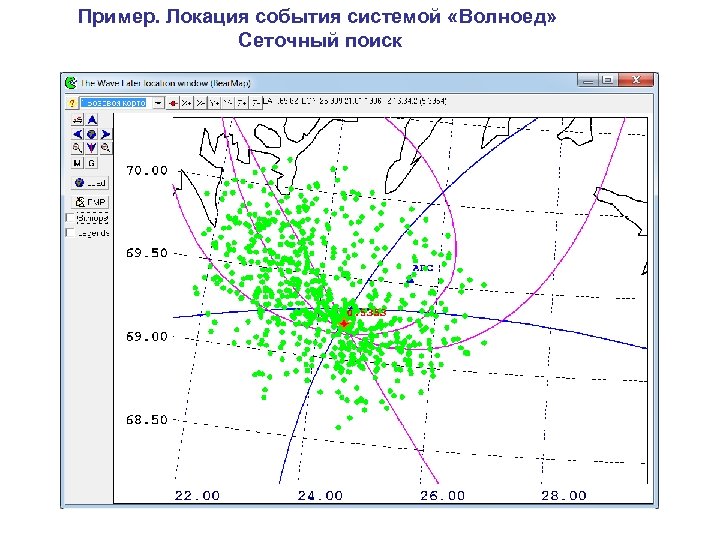
Пример. Локация события системой «Волноед» Сеточный поиск

Ошибки локации Главные источники ошибок: 1. Неправильная идентификация вступлений волн (Особенности строения среды, маскирующие некоторые приходы волн) 2. Неточность измерения времен вступлений сейсмических волн 3. Неточность используемых скоростных моделей (годографов) 4. Ошибки привязки ко времени Пример к п. 1. Событие на арх. Шпицберген. Видны многократные приходы P-волны. Линии засечек (по первым видимым приходам) сильно расходятся. Объяснение – видимый приход S не первый (первые приходы замаскированы кодой P-волны)

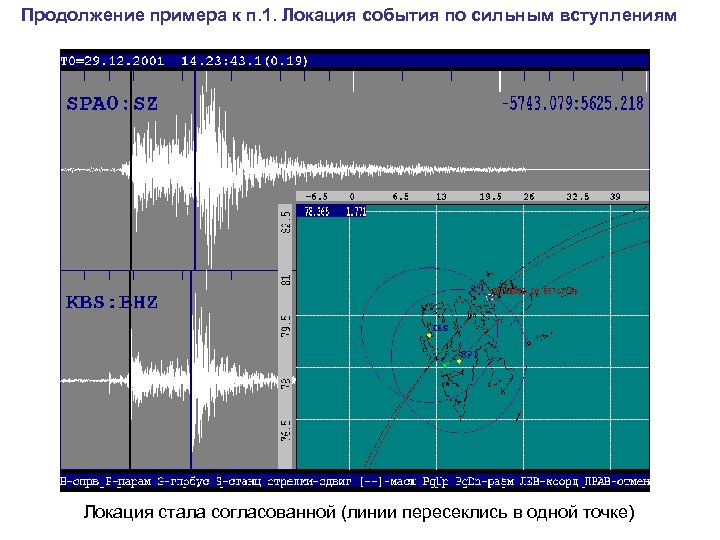
Продолжение примера к п. 1. Локация события по сильным вступлениям Локация стала согласованной (линии пересеклись в одной точке)

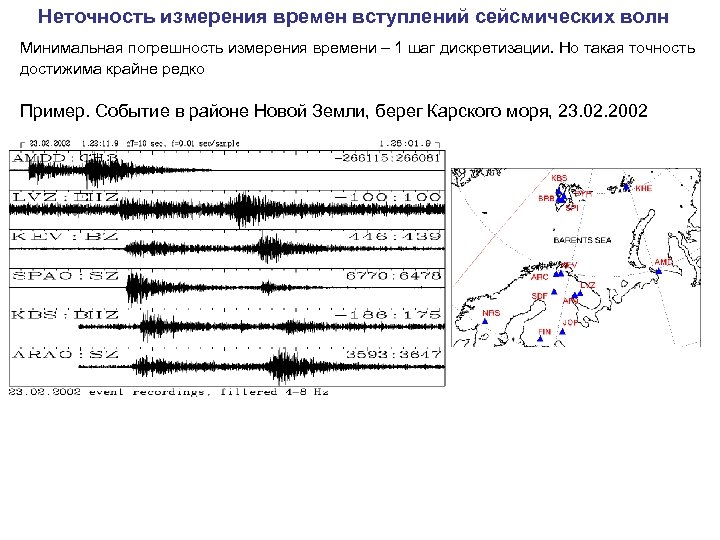
Неточность измерения времен вступлений сейсмических волн Минимальная погрешность измерения времени – 1 шаг дискретизации. Но такая точность достижима крайне редко Пример. Событие в районе Новой Земли, берег Карского моря, 23. 02. 2002

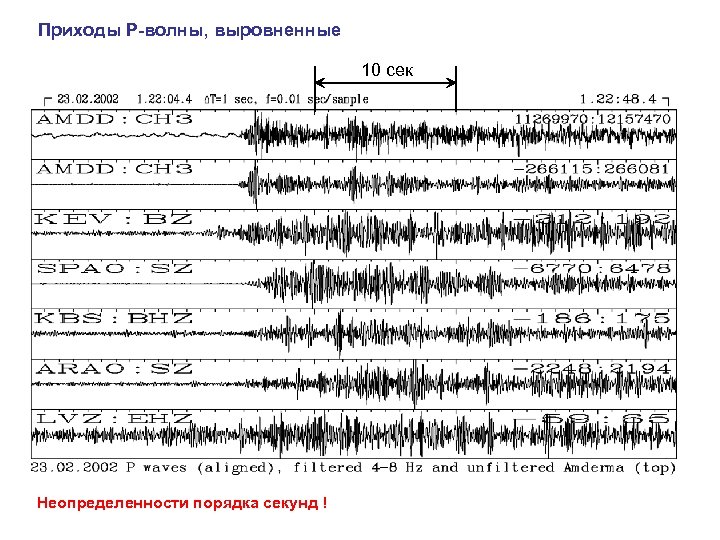
Приходы P-волны, выровненные 10 сек Неопределенности порядка секунд !

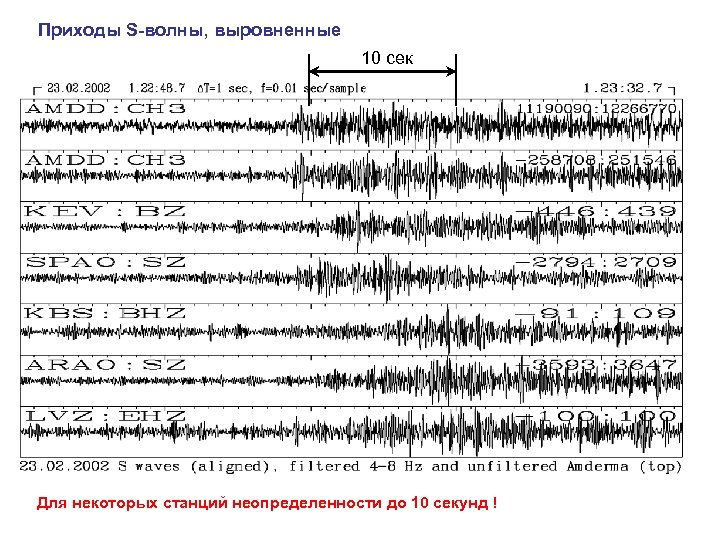
Приходы S-волны, выровненные 10 сек Для некоторых станций неопределенности до 10 секунд !

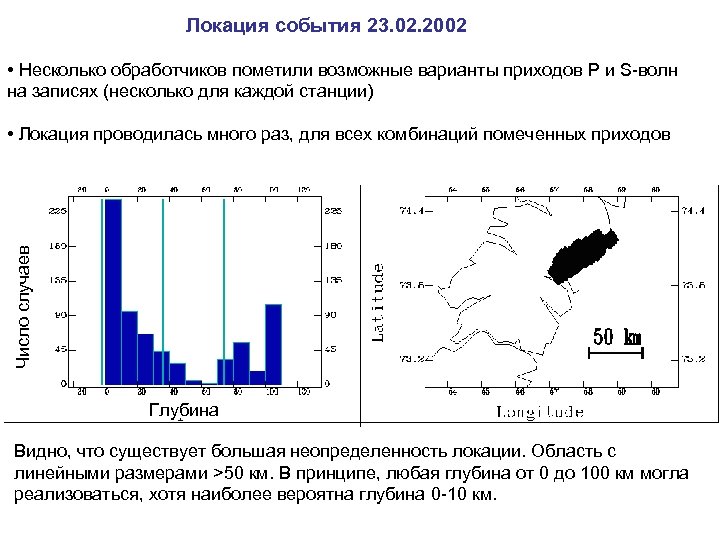
Локация события 23. 02. 2002 • Несколько обработчиков пометили возможные варианты приходов P и S-волн на записях (несколько для каждой станции) Число случаев • Локация проводилась много раз, для всех комбинаций помеченных приходов Глубина Видно, что существует большая неопределенность локации. Область с линейными размерами >50 км. В принципе, любая глубина от 0 до 100 км могла реализоваться, хотя наиболее вероятна глубина 0 -10 км.

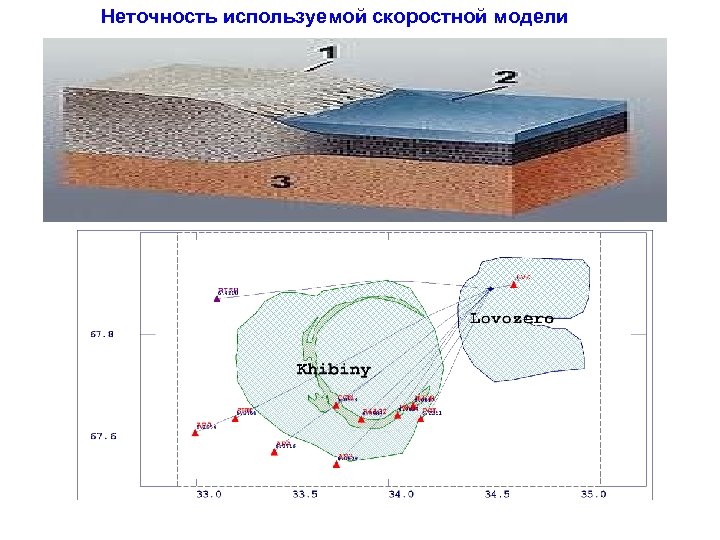
Неточность используемой скоростной модели

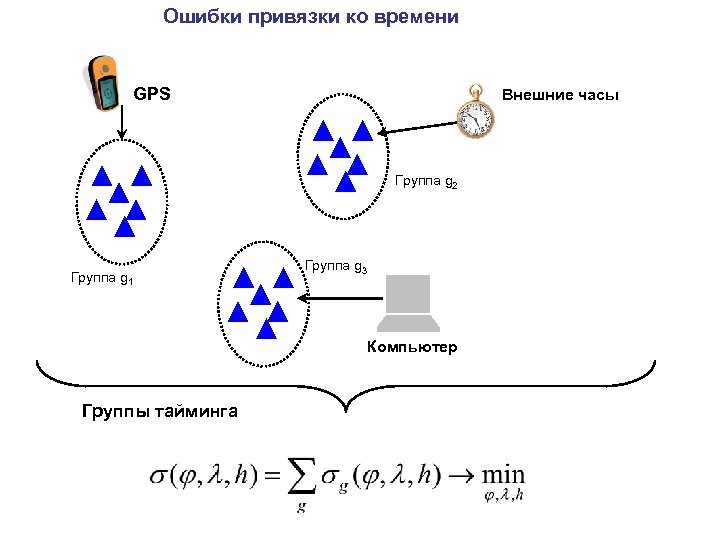
Ошибки привязки ко времени GPS Внешние часы Группа g 2 Группа g 1 Группа g 3 Компьютер Группы тайминга

Локация событий в неоднородных средах Необходимо уметь вычислять время пробега волн от одной точки до другой Распространенным методом учета является введение станционных поправок (Source Specific Station Correction). Для каждой конкретной станции время пробега от источника до станции выражается в виде: Поправки считаются заранее для каждой конкретной станции некими внешними программами Достоинства: простота алгоритма локации, быстрота счета Недостатки: трудность перехода на другую скоростную модель, трудность подключения новых станций (необходимо пересчитывать таблицы поправок) Альтернатива: регионализация по Бондарю, локация на графе

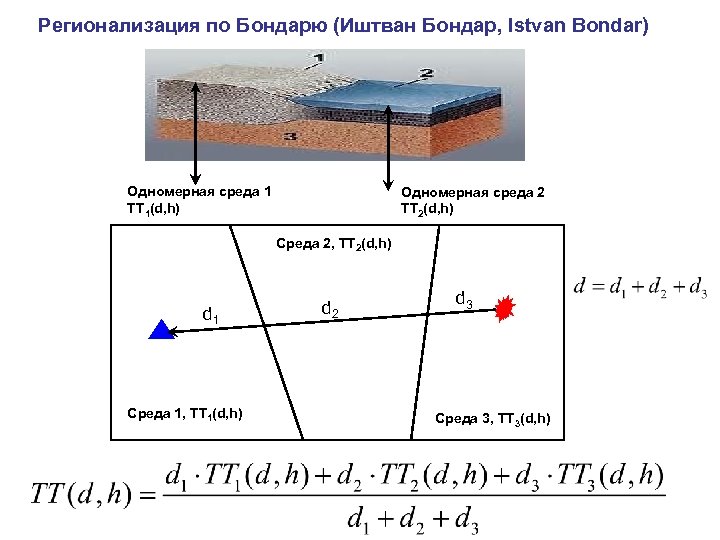
Регионализация по Бондарю (Иштван Бондар, Istvan Bondar) Одномерная среда 1 TT 1(d, h) Одномерная среда 2 TT 2(d, h) Среда 2, TT 2(d, h) d 1 Среда 1, TT 1(d, h) d 2 d 3 Среда 3, TT 3(d, h)

Локация на стохастическом графе (программа SK) • Локация сейсмических событий по первым временам прихода волн на сейсмостанции в произвольной трехмерной среде • Оценка ошибок локации, вызванных: - неточностью используемой скоростной модели - неучетом пустот (выработок), рельефа - ошибками измерений времен приходов волн на станции • Трассировка лучей (путей пробега наибыстрейших волн) в среде ПРИНЦИП РАБОТЫ ПРОГРАММЫ SK • Трехмерная среда заменяется на стохастический граф (набор вершин и связей между ними). Длина связи соответствует времени пробега волны между вершинами. Длина пути между двумя вершинами графа соответствует времени пробега волны между точками среды. • Расчет времен пробега, трассировка лучей и локация производятся с помощью волнового алгоритма, разновидности которого известны в теории графов как алгоритмы Ли и Дейкстры. Волновой алгоритм позволяет для заданной вершины графа быстро рассчитать кратчайшие пути из нее во все другие вершины.

СТОХАСТИЧЕСКИЙ ГРАФ Характеризуется плотностью density (числом вершин на единицу объема) и радиусом связи radius (все вершины, расстояния между которыми меньше radius связываются). В программе параметры density и radius являются функциями координат и могут быть заданы пользователем. Таким образом, можно сконфигурировать граф с большим числом вершин в наиболее интересных участках, например, вокруг сейсмостанций и в зонах локации Пример генерации вершин графа в программе SK. Пользователем задана двухслойная среда, плотность точек в верхнем слое выше. В нее вкраплены два объемных тела, изображающие Хибинский и Ловозерский массивы. В них плотность точек графа еще выше. Количественные ограничения: до 10 000 вершин и 40 000 связей

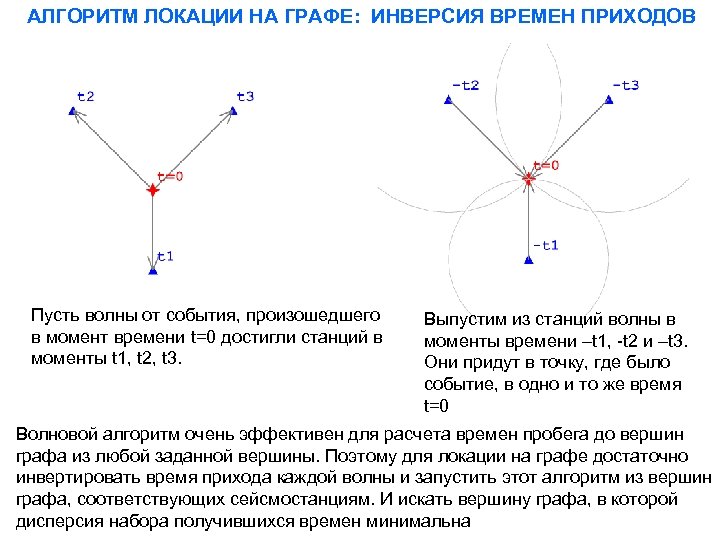
АЛГОРИТМ ЛОКАЦИИ НА ГРАФЕ: ИНВЕРСИЯ ВРЕМЕН ПРИХОДОВ Пусть волны от события, произошедшего в момент времени t=0 достигли станций в моменты t 1, t 2, t 3. Выпустим из станций волны в моменты времени –t 1, -t 2 и –t 3. Они придут в точку, где было событие, в одно и то же время t=0 Волновой алгоритм очень эффективен для расчета времен пробега до вершин графа из любой заданной вершины. Поэтому для локации на графе достаточно инвертировать время прихода каждой волны и запустить этот алгоритм из вершин графа, соответствующих сейсмостанциям. И искать вершину графа, в которой дисперсия набора получившихся времен минимальна

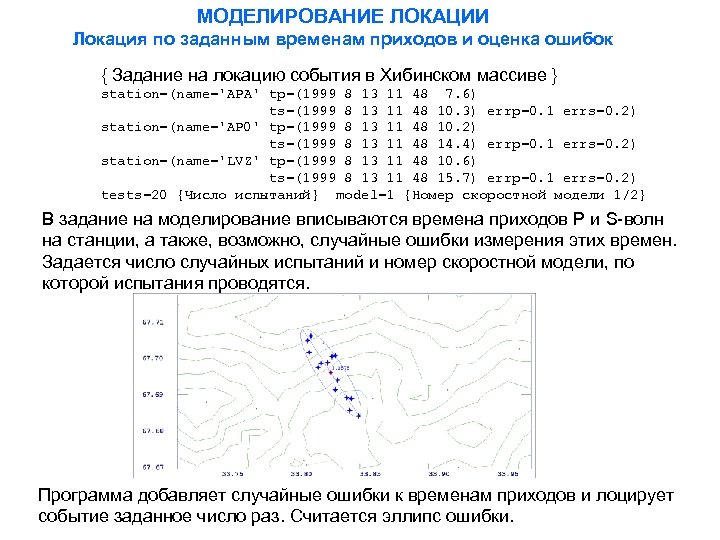
МОДЕЛИРОВАНИЕ ЛОКАЦИИ Локация по заданным временам приходов и оценка ошибок { Задание на локацию события в Хибинском массиве } station=(name='APA' tp=(1999 8 13 11 48 7. 6) ts=(1999 8 13 11 48 10. 3) errp=0. 1 errs=0. 2) station=(name='AP 0' tp=(1999 8 13 11 48 10. 2) ts=(1999 8 13 11 48 14. 4) errp=0. 1 errs=0. 2) station=(name='LVZ' tp=(1999 8 13 11 48 10. 6) ts=(1999 8 13 11 48 15. 7) errp=0. 1 errs=0. 2) tests=20 {Число испытаний} model=1 {Номер скоростной модели 1/2} В задание на моделирование вписываются времена приходов P и S-волн на станции, а также, возможно, случайные ошибки измерения этих времен. Задается число случайных испытаний и номер скоростной модели, по которой испытания проводятся. Программа добавляет случайные ошибки к временам приходов и лоцирует событие заданное число раз. Считается эллипс ошибки.

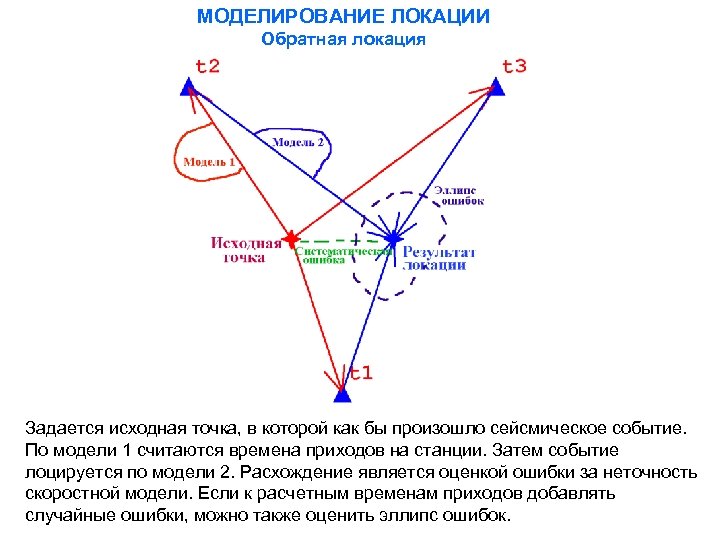
МОДЕЛИРОВАНИЕ ЛОКАЦИИ Обратная локация Задается исходная точка, в которой как бы произошло сейсмическое событие. По модели 1 считаются времена приходов на станции. Затем событие лоцируется по модели 2. Расхождение является оценкой ошибки за неточность скоростной модели. Если к расчетным временам приходов добавлять случайные ошибки, можно также оценить эллипс ошибок.

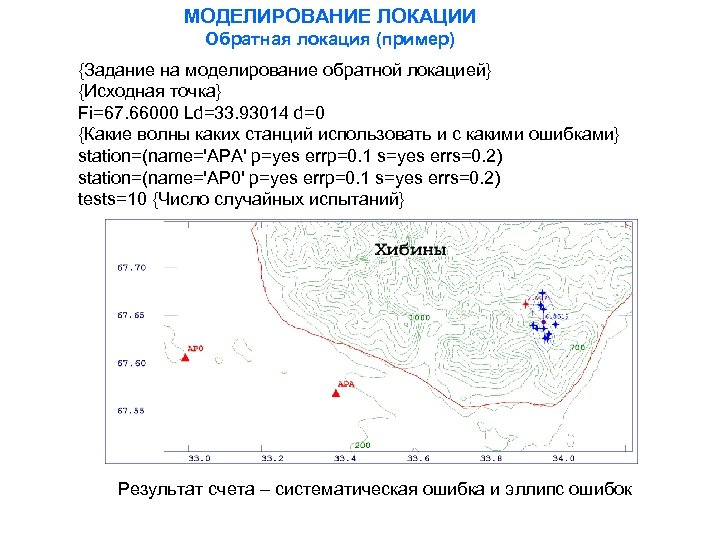
МОДЕЛИРОВАНИЕ ЛОКАЦИИ Обратная локация (пример) {Задание на моделирование обратной локацией} {Исходная точка} Fi=67. 66000 Ld=33. 93014 d=0 {Какие волны каких станций использовать и с какими ошибками} station=(name='APA' p=yes errp=0. 1 s=yes errs=0. 2) station=(name='AP 0' p=yes errp=0. 1 s=yes errs=0. 2) tests=10 {Число случайных испытаний} Результат счета – систематическая ошибка и эллипс ошибок

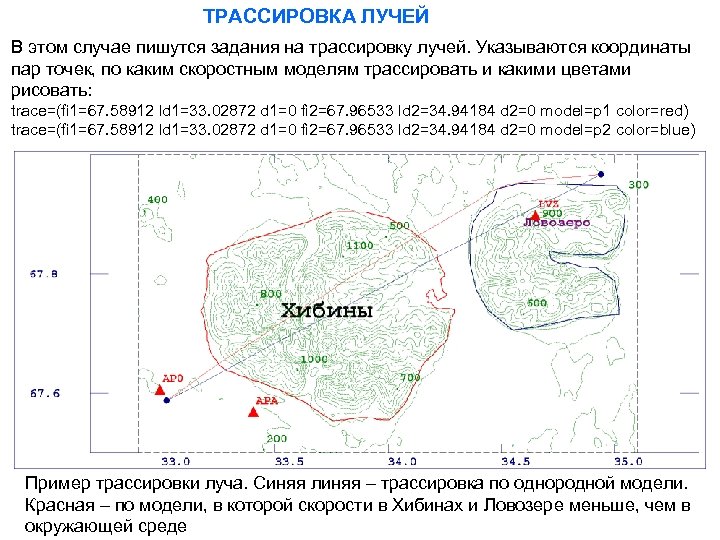
ТРАССИРОВКА ЛУЧЕЙ В этом случае пишутся задания на трассировку лучей. Указываются координаты пар точек, по каким скоростным моделям трассировать и какими цветами рисовать: trace=(fi 1=67. 58912 ld 1=33. 02872 d 1=0 fi 2=67. 96533 ld 2=34. 94184 d 2=0 model=p 1 color=red) trace=(fi 1=67. 58912 ld 1=33. 02872 d 1=0 fi 2=67. 96533 ld 2=34. 94184 d 2=0 model=p 2 color=blue) Пример трассировки луча. Синяя линяя – трассировка по однородной модели. Красная – по модели, в которой скорости в Хибинах и Ловозере меньше, чем в окружающей среде

СПАСИБО ЗА ВНИМАНИЕ !