РС 2 КУ Раздел № 2

РС 2 КУ Раздел № 2 Показательная и логарифмическая
Выполните действия: 21+(-41)-1= (-1)²= 0· 1013=
? Какие числовые множества вам известны? 1 -4 -5
R- множество действительных чисел N ={1, 2, 3, …, n}- множество натуральных
Записать известные формулы сокращенного умножения в справочник!
Упростить выражение и найти его значение при х=1, у=2: • а) (х-1)²-у(х+1)+ху= •
Повторение пройденного: 1. Найти нули функции и записать ее область определения:
Вид уравнения Название Решение 1 ax+b=0
1. Решить уравнения: а) х· 0=87 б) 0·х=0 в) г) (½)·х=6
2. Решить уравнения: а) 2 х-6 х+9=4 -4 х+5 б) (х+8)(х-7)=0
(все данные занести в справочник) Неравенства Строгие > <
№ 1. Решить неравенство методом интервалов: (х+2)(х-3)(х-5)≥ 0 • Решение.
№ 2. Решить неравенство методом интервалов Решение.
Домашнее задание. 1. Решить уравнение: х⁵-х⁴-2 х³+2 х²-3
Скачать презентацию РС 2 КУ Раздел № 2 Скачать презентацию РС 2 КУ Раздел № 2

1- Повторен.ppt

  • Количество слайдов: 14

> РС 2 КУ Раздел № 2 Показательная и логарифмическая РС 2 КУ Раздел № 2 Показательная и логарифмическая функция. Тема№ 1: «Повторение профессионально- значимого алгебраического материала» .

> Выполните действия: 21+(-41)-1= (-1)²= 0· 1013= Выполните действия: 21+(-41)-1= (-1)²= 0· 1013= (-1)³= (-25)· 2= (-2)³= (-30)·(-5)= (½)²= (-1)-(-24)= (¾)²= (-60): 2= 5º= (-21): (-3)= 7¹= 0: (-1356)= 8ˉ¹= (-¾): (½) (⅝)ˉ² =

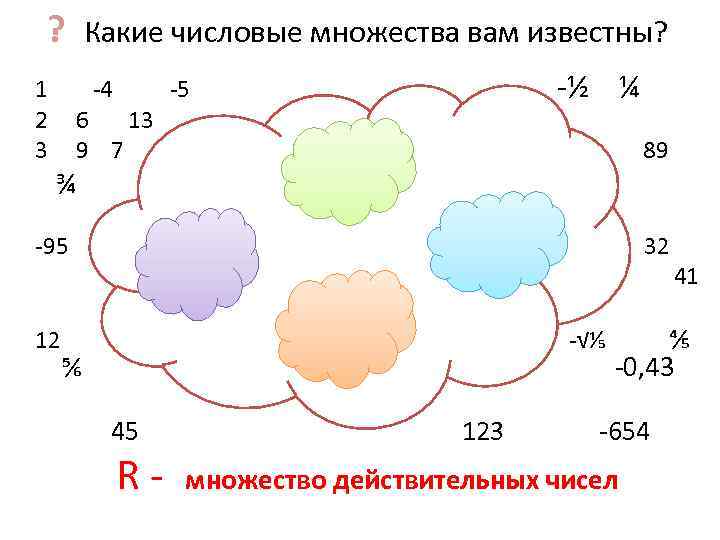> ? Какие числовые множества вам известны? 1 -4 -5 ? Какие числовые множества вам известны? 1 -4 -5 -½ ¼ 2 6 13 3 9 7 89 ¾ -95 32 41 12 -√⅕ ⅘ ⅚ ℮ -0, 43 45 123 -654 R- множество действительных чисел

>R- множество действительных чисел N ={1, 2, 3, …, n}- множество натуральных R- множество действительных чисел N ={1, 2, 3, …, n}- множество натуральных чисел Z={…, -n, …, -3, -2, -1, 0, 1, 2, 3, …, n }- множество целых чисел Q={m/n, где m€Z, n≠ 0 }- множество рациональных чисел Q={√ 2, ∏≈3, 14, ℮≈2, 7} множество иррациональных чисел

>Записать известные формулы сокращенного умножения в справочник! Записать известные формулы сокращенного умножения в справочник!

>Упростить выражение и найти его значение при х=1, у=2: • а) (х-1)²-у(х+1)+ху= • Упростить выражение и найти его значение при х=1, у=2: • а) (х-1)²-у(х+1)+ху= • б) (х-у)(х+у)+у²= • Разложить на множители: (х-1)²+у(х-1)=

> Повторение пройденного: 1. Найти нули функции и записать ее область определения: Повторение пройденного: 1. Найти нули функции и записать ее область определения: определения: 2. Найти f(-2)= 2. Найти f(5)=

> Вид уравнения Название Решение 1 ax+b=0 Вид уравнения Название Решение 1 ax+b=0 Линейное 1) а≠ 0, корень: х=b/а где a, b- R числа уравнение с одной 2) 0·х=0 х=R переменной 3) 0·х=b (а=0, b≠ 0), корней нет 1) D>0, то 2 корня: х= 2 ax²+bх+с=0 Квадратное где a≠ 0 , b, с уравнение 2) D<0, то корней нет - R числа 3) D=0, то 1 корень: х=-b/2 а 3 х²=а неполное (х-а)(х+а)=0 х=±√а квадратное уравнение 4 Дробно- рациональное уравнение 5 Уравнение n-ой степени 6 ax⁴+bх²+с=0 Биквадратное х²= у → aу²+bу+с=0 где a≠ 0 , b, с -R числа уравнение

> 1. Решить уравнения: а) х· 0=87 б) 0·х=0 в) г) (½)·х=6 1. Решить уравнения: а) х· 0=87 б) 0·х=0 в) г) (½)·х=6 д) х²=25 е) х²= -81 ж) х²-49=0

> 2. Решить уравнения: а) 2 х-6 х+9=4 -4 х+5 б) (х+8)(х-7)=0 2. Решить уравнения: а) 2 х-6 х+9=4 -4 х+5 б) (х+8)(х-7)=0 в) г) х³-5 х²+6 х=0 д) 9 х⁴-10 х²+1=0 е) х³-3 х²-х+3=0

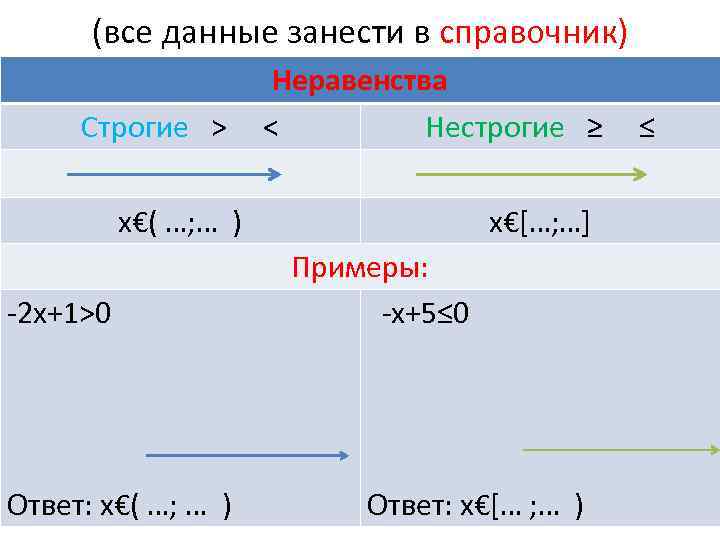> (все данные занести в справочник) Неравенства Строгие > < (все данные занести в справочник) Неравенства Строгие > < Нестрогие ≥ ≤ х€( …; … ) х€[…; …] Примеры: -2 х+1>0 -х+5≤ 0 Ответ: х€( …; … ) Ответ: х€[… ; … )

>№ 1. Решить неравенство методом интервалов: (х+2)(х-3)(х-5)≥ 0 • Решение. № 1. Решить неравенство методом интервалов: (х+2)(х-3)(х-5)≥ 0 • Решение.

>№ 2. Решить неравенство методом интервалов Решение. № 2. Решить неравенство методом интервалов Решение.

> Домашнее задание. 1. Решить уравнение: х⁵-х⁴-2 х³+2 х²-3 Домашнее задание. 1. Решить уравнение: х⁵-х⁴-2 х³+2 х²-3 х+3=0 2. Решить неравенство: