РОЗВ ’ ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ

РОЗВ ’ ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ • 2. 1 Системи лінійних рівнянь • 2. 2 Матричный метод • 2. 3 Правило Крамера • 2. 4 Метод Гаусса

Лінійною системою m рівнянь з n невідомими х 1 , х 2 , … х n називається система виду . . . , . . . 2211 22222121 11212111 mnmnmm nn nn bxaxaxa де числа а 11 , а 12 , … а mn – коефіцієнти системи. Система рівнянь, що має принаймні один розв’язок, називається сумісною. Якщо система не має розв’язків, то вона називається несумісною. (2. 1 )2. 1 Системилінійнихрівнянь

Сумісна система, що має єдиний розв’язок, називається визначеною , система, що має більш ніж один розв’язок – невизначеною. Найвищий порядок ненульового мінору називається рангом матриці і позначається rang A. називаються основною і розширеною матрицями системи , відповідно. Теорема (Кронекера-Капеллі): Для того чтоб лінійна система була сумісною, необхідно і достатньо, чтоб ранг розширеної матриці цієї системи дорівнював рангу її основної матриці. , . . . 21 22221 11211 mnmm n n aaa aaa A mmnmm n n b b b aaa aaa b. A. . . 2 1 21 22221 11211 Матриц і

Система рівнянь (2. 1) е квівалентна системі А х= b , записаній в матричній формі. Якщо | А | 0, то матриця А називається невиродженою і для неї існує обернена матриця А -1, . . . 1 21 22212 12111 1 nnnn n n AAA AAA A A x = А -1 b. 2. 2 Матричный метод де А ij – алгебраїчні доповнення відповідних елементів матриці. Тоді

Приклад : Розвязати систему рівнянь . 3 , 12 , 024 32 321 xx xxx матричним методом. , 011)2(40018 110 121 124 A отже , А – невироджена і існує A ij =(-1) i + j М ij. , 3)12(1 11 12 )1(11 11 A , 1)01()1( 10 11 )1(21 12 A , 1)01(1 10 21 )1(31 13 A , 1)12()1( 11 12 )1(12 21 A , 4)04(1 10 14 )1(22 22 A , 4)04()1( 10 24 )1( 32 23 A.

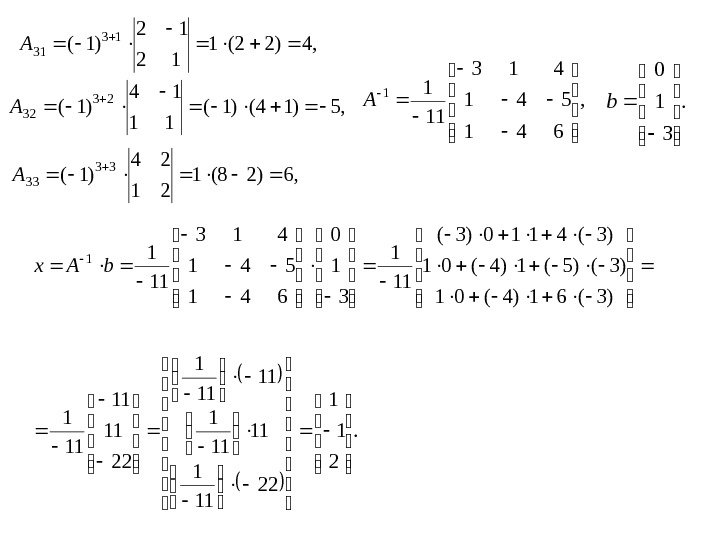, 4)22(1 12 12 )1( 13 31 A , 5)14()1( 11 14 )1( 23 32 A , 6)28(1 21 24 )1( 33 33 A, 641 541 413 11 11 A. 31 0 b . 2 1 1 22 11 11 1 22 11 11 11 1 )3(61)4(01 )3()5(1)4(01 )3(4110)3( 11 1 3 1 0 641 541 413 11 11 b. Ax

2. 3 Правило Крамера Матрична рівність х = А -1 b можна записати у вигляді nnnnn nnnnn n n nb. Ab. Ab. A A b b b AAA AAA A x x x. . . 1. . . 2211 2222112 1221111 2 1 21 22212 12111 2 1 звідки, з урахуванням теореми Лапласа випливає, що , i ix i =1. . n , де = | А | , а i – визначник, одержаний з заміною i -го стовпчика стовпцем вільних членів

Правило Крамера : якщо визначник системи рівнянь відмінний від 0, то вона має єдиний розв’язок який визначається за формулами Крамера. Існування цього розв’язку випливає з теореми Кронекера-Капеллі, оскільки зі співвідношення | А | 0 випливає, що ранг основної матриці А дорівнює п , а ранг розширеної матриці, що містить п рядків, більше числа п бути не може і тому дорівнює рангу основної матриці.

Приклад : Розв’язать систему рівнянь , 3 , 12 , 024 32 321 xx xxx за формулами Крамера. , 011 110 121 124 A Отже, система має єдиний розв ’ язок , визначений за формулами Крамера. , , 3 3 2 2 1 1 xxx , 11 113 121 120 1 , 1 11 1 x , 11 130 111 104 2 , 1 1111 2 2 x. 2 11 22 3 3 x ,

Дослідженнясистеми • Якщо det ≠ 0, то система має єдиний розв ’ язок. • Якщо det = 0 і принаймні дин з визначників det i не дорівнює 0, то система несумісна. • Якщо det = det i = 0, то система має нескінчену множину розвязків або не має розв ’ язків.

2. 4 Метод Гаусса Елементарними перетвореннями матриці називаются наступні операції: а) перестановка двох рядків матриці; б) множення рядка на число 0; в) додавання до одного рядка матриці іншого її рядка, помноженої на число 0; г) транспонування матриці. Елементарні перетворення матриці не змінюють її рангу. Тому при обчисленні рангу матриці, вона за допомогою елементарних перетворень зводиться до матриці В , ранг якої легко знаходиться. Якщо A = rang B , то A B.

Розглянемо систему лінійних рівнянь nnn nn d d b c cc aaa. . 00. . . 21 222 11211 або до трапецієподібного виду mmnmm nm nm d d b cc ccc aaaa. . . . 00. . . 21 2222 111211Її розширену матрицю елементарними перетвореннями над рядкаси можна звести . . . , . . . 2211 22222121 11212111 mnmnmm nn nn bxaxaxa або до трикутного виду (2. 2) (2. 3)

Матриця (2. 2) відповідає перетвореній системі . . , . . . 22222 11212111 nnnn nn nn dxcxc bxaxaxa В цьому випадку , починаючи з останнтього рівняння, знаходим послідовно значения невідомих x n , x n -1 , … x 1 єдиним чином, якщо c nn 0, … c 22 0, a 11 0. Якщо у деякому i -му рядку всі с ij =0, а d i 0, то це свідчить про те, що что система несумісна, оскільки в даному випадку rang([ A |b]) rang( A ).

Приклад : Розв’язать систему рівнянь , 3 , 12 , 024 32 321 xx xxx методом Гаусса. . 3 1 0 110 121 124 b. A Розширена матриця системи має вид : Переставим другий рядок на місце першого , перший на місце третього, а третій на місце другого, одержим: . 0 31 124 110 121 Від першого рядка помноженого на 4 віднімемо 3 -й: .

. 22 31 1100 110 121 Від другого рядка помноженого на 6 віднімемо 3 -й : Матриця зведена до трикутного виду, їй відповідає перетворена система рівнянь: . 2211 , 3, 123 32 321 xxx Знаходим розв ’ язок цієї системи, починаючи з останнього рівняння : . 2 11 22 , 1323 , 112)1(212 3 32 321 x xx xxx

Для трапецієвидної матриці (2. 3) перетворена система має вид : . . . . , . . . 22222 11212111 mnmnmmm nn nn dxcxс dxcxc bxaxaxa Звідки знаходим . . . . , . . . 11 2121222222 111111212111 nmnmmmmmmm nnmmmm xcxcdxс xcxcdxcxc xaxabxaxaxa Надаючи змінним x m +1 , x m +2 , … x n довільні значення, знаходим із системи x m , x m -1 , … x 1. Таким чином, метод Гаусса надає можливість не тільки розв’язать систему, але і дати відповідь на запитання про її сумісність.

Приклад : За допомогою метода Гаусса розвязать систем у . 052 , 023 , 0323 4321 xxxx. 5211 1123 1323 4 2400 1710 5211 Оскільки, rang( A )=3<4= n , то система имеет нескінченну множин розв’язків. Основна матриця системи має вид: Поміняємо перший і третій рядки місцями : . 1323 1123 5211 Від першого рядка помноженого на 3 віднімемо послідовно другій, а потім третій рядок. Потім від другого рядка віднімемо третій, одержимо: 04 400 710 211 123 M — базисний мінор, х 1 , х 2 , х 3 – базисні змінні , х 4 – вільна змінна.

Нехай х 4 =2 t , t R , тоді : Матриця зведена до трапецієвидної форми, їй відповідає перетворена система рівнянь: . 024 , 0147 , 052 43 4321 xx xxxx Знаходим розвязок цієї системи, починаючи з останнього рівняння. . 4 22 4 2 , 352147147 , 232523552 4 3 4321 t tx x tttxxx ttttxxxx