Rough-Cut Capacity Planning in SCM EIN 5346 Logistics

Rough-Cut Capacity Planning in SCM EIN 5346 Logistics Engineering Fall, 2017

Rough-Cut Capacity Planning in SCM Theories & Concepts

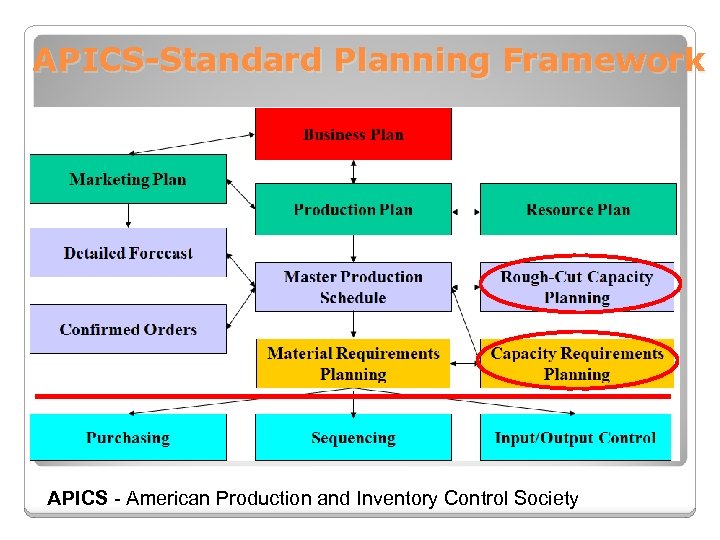APICS-Standard Planning Framework APICS - American Production and Inventory Control Society

Rough-cut Capacity Planning Main goal in rough-cut capacity planning is to identify where overloading or under-loading of production capacity occurs and revise the MPS as required. • Overloading means that too much production of products has been planned in the facility and insufficient capacity exists to produce planned quantities of products required in MPS. • Under-loading means that not enough production of products has been planned to fully load the facility.

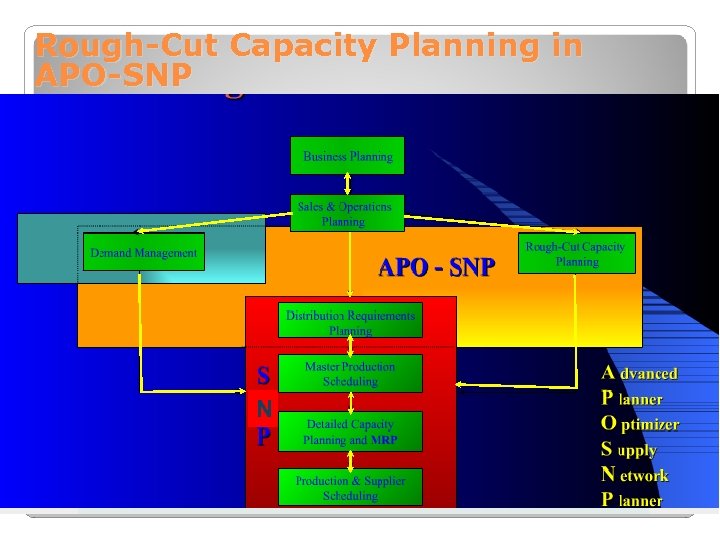Rough-Cut Capacity Planning in APO-SNP N

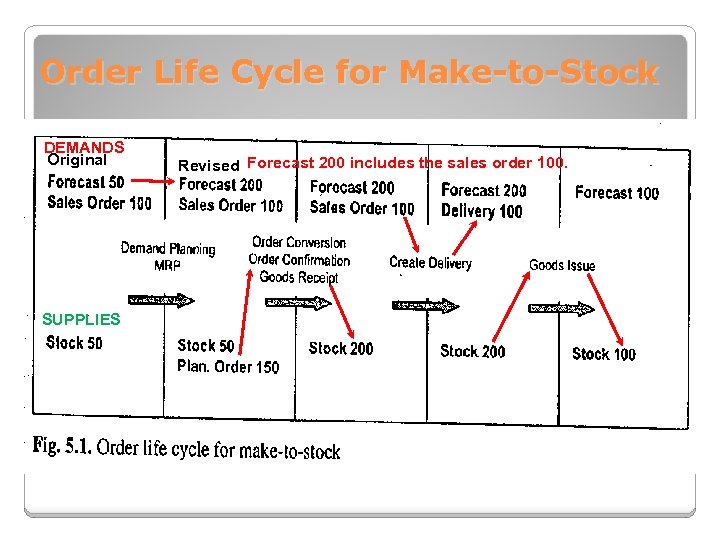Order Life Cycle for Make-to-Stock DEMANDS Original SUPPLIES Revised Forecast 200 includes the sales order 100.

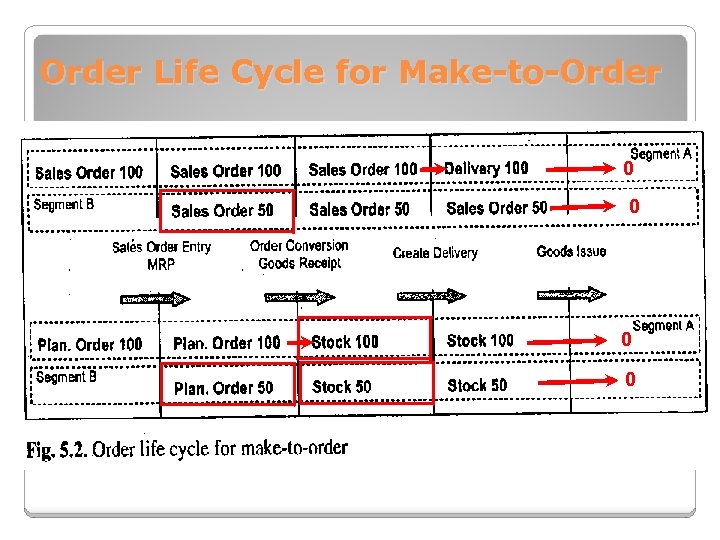Order Life Cycle for Make-to-Order 0 0

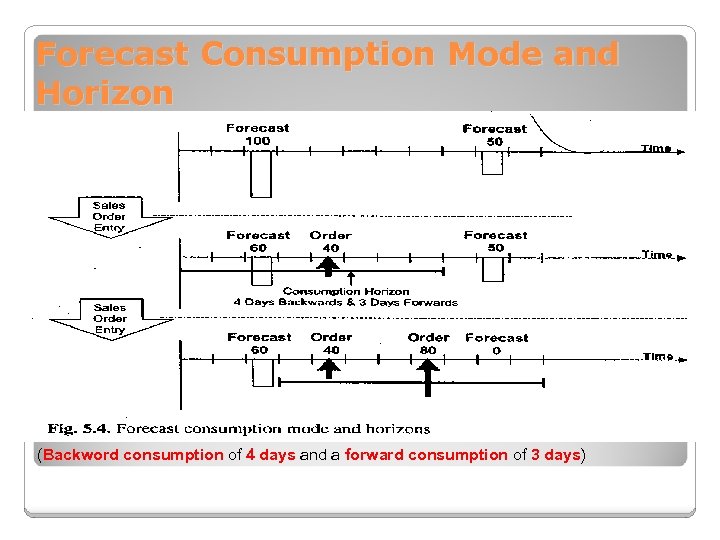Forecast Consumption Mode and Horizon (Backword consumption of 4 days and a forward consumption of 3 days)

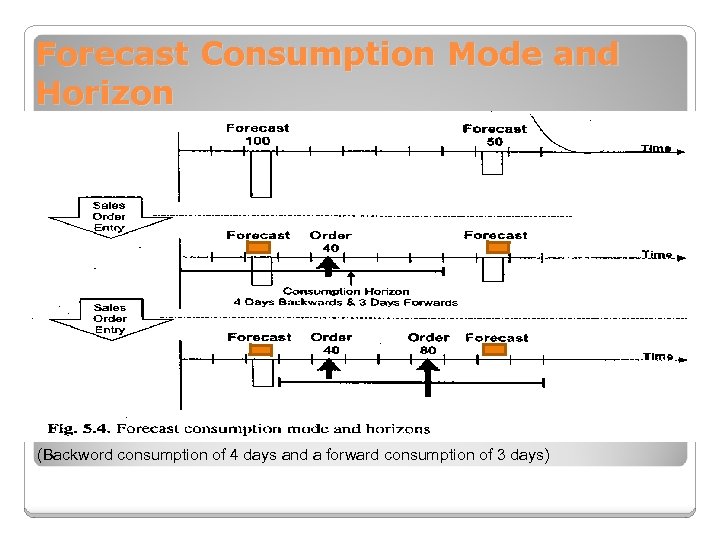Forecast Consumption Mode and Horizon (Backword consumption of 4 days and a forward consumption of 3 days)

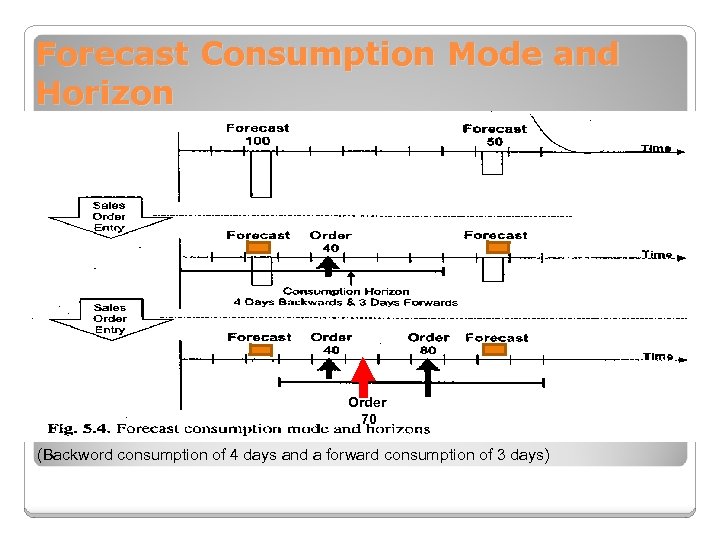Forecast Consumption Mode and Horizon Order 70 (Backword consumption of 4 days and a forward consumption of 3 days)

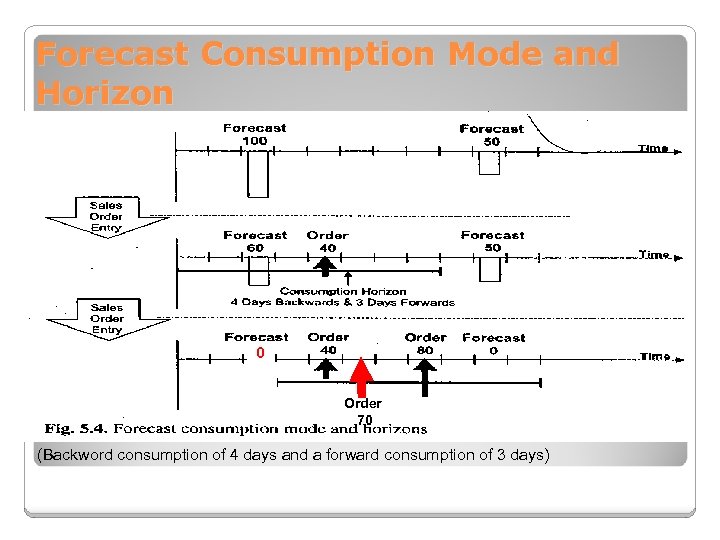Forecast Consumption Mode and Horizon 0 Order 70 (Backword consumption of 4 days and a forward consumption of 3 days)

Transactional Data for Transferring • Starting from a demand plan, SNP checks the resource capacities and delivers a medium/long-term plan for the estimated sales volumes. • The plan includes 1) quantities to be transported between locations (e. g. , DC-customer, or plant-DC) and 2) quantities to be produced (and procured), taking available capacity into consideration. • SNP creates planned orders, purchase requisitions, and stock transfers that can be transferred directly to the connected OLTP systems.

Capacity Levelling Capacity leveling supports the following resource categories: • Production resources in APO (Work centers in ERP) • Transportation resources

Capacity Levelling Profile The main settings in the capacity leveling profile are scheduling direction, prioritization, and method. • Scheduling Direction controls whether Forward, Backward or Combined scheduling is used. • Prioritization for the heuristic run defines how leveling determines the sequence of orders. The two possible choices for prioritization (to be sorted by ascending or descending order) are • by order size or • by product priority. • Method choices are • Heuristic, • Optimizer

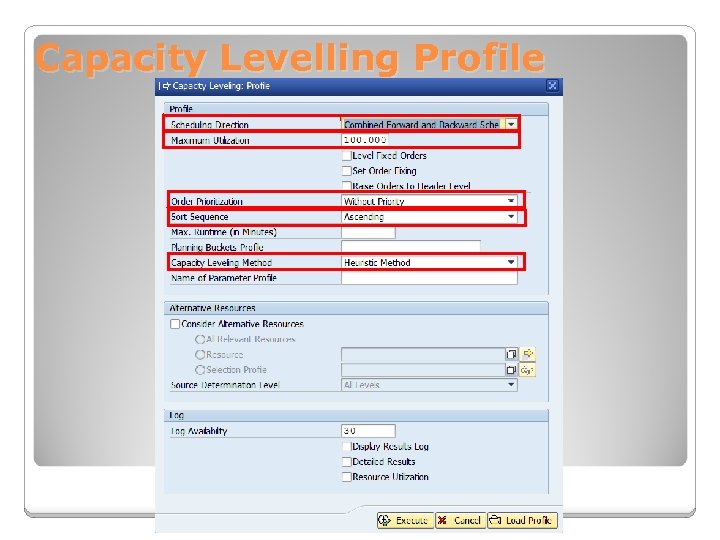Capacity Levelling Profile

Heuristics-based Capacity Levelling • Heuristic-based capacity leveling compares, period by period, • If resource is found overloaded, the system first selects all the activities or orders that cause the overload in this period. • It sorts these orders according to the priority one by one until the required maximum resource utilization is reached.

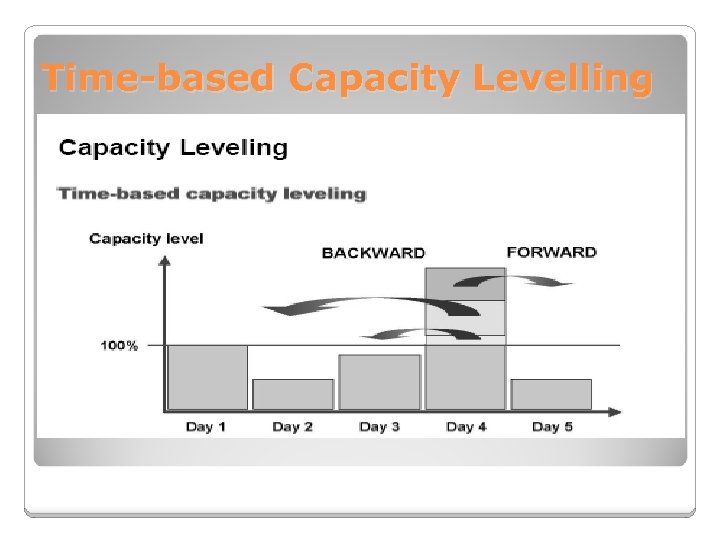Time-based Capacity Levelling

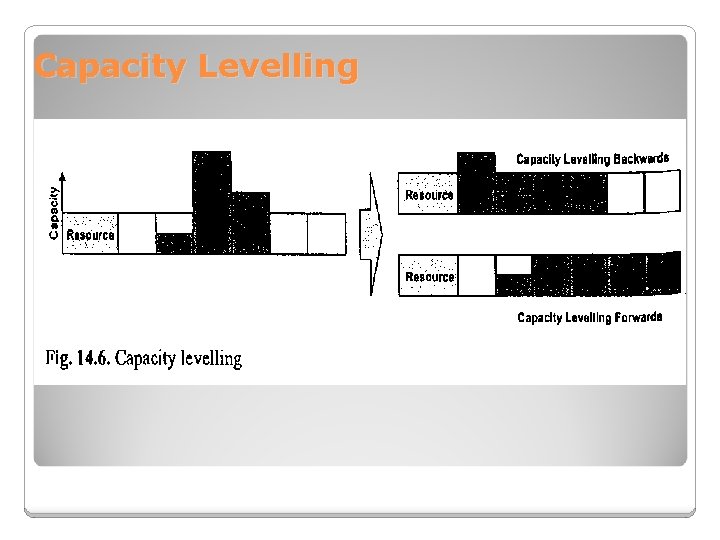Capacity Levelling

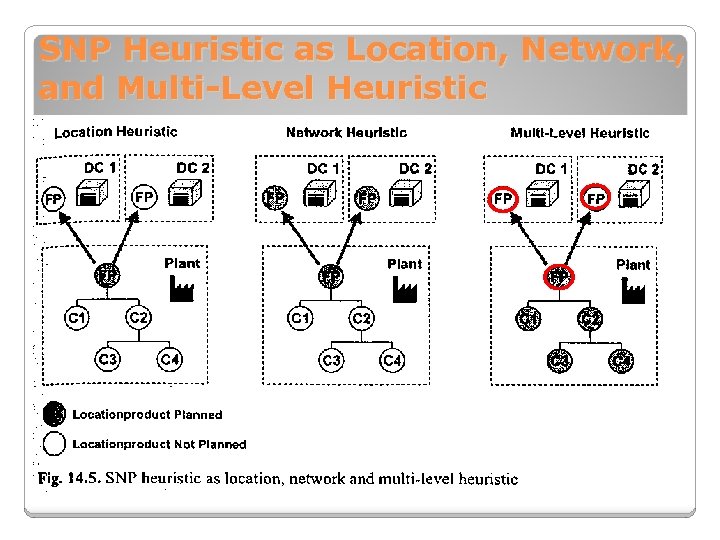SNP Heuristic as Location, Network, and Multi-Level Heuristic

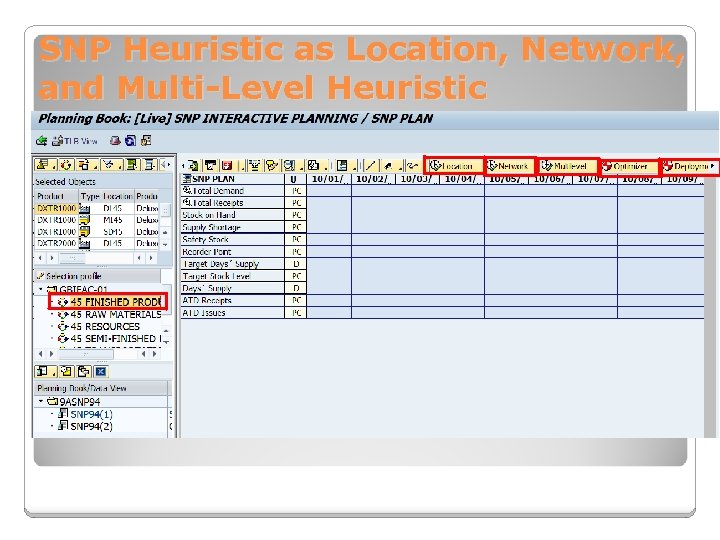SNP Heuristic as Location, Network, and Multi-Level Heuristic

Operation Research (OR) Operation research refers to the application of quantitative methods and techniques to business problems in order to best utilize a company’s resources. OR is used by many leading companies to optimize their limited resources in order to maximize their profits or minimize their costs. Linear programming (LP) is one of the most important tools of operation research.

Linear Programming (LP)

Linear Programming (LP) Five common types of LP problems: • Product mixed • Ingredient mix • Transportation • Production plan • Assignment

Five common types of LP problems

Five common types of LP problems

Steps in Formulating LP Problems 1. Define the objective 2. Define the decision variables 3. Write the mathematical function for the objective (objective function) 4. Write a one- or two-word description of each constraints 5. Write the right-hand side (RHS) of each constraint, including the unit of measure. 6. Write<=, =, or >= for each equation 7. Write all the decision variables on the left-hand side of each constraints 8. Write the coefficient for each decision variable in each constraint.

Formulating LP

Formulating LP

Formulation LP

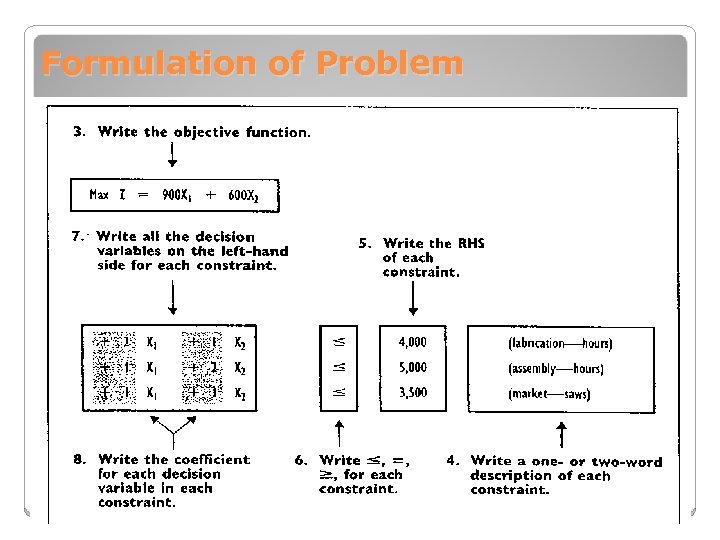Formulation of Problem

Objective and Constraints

Steps in Graphical Solution Method

Graphical Solution

Graphical Solution

Graphical Solution

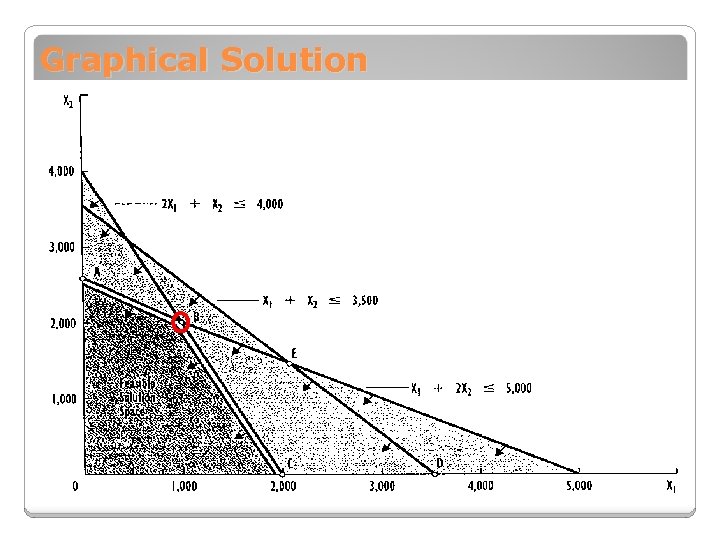Graphical Solution

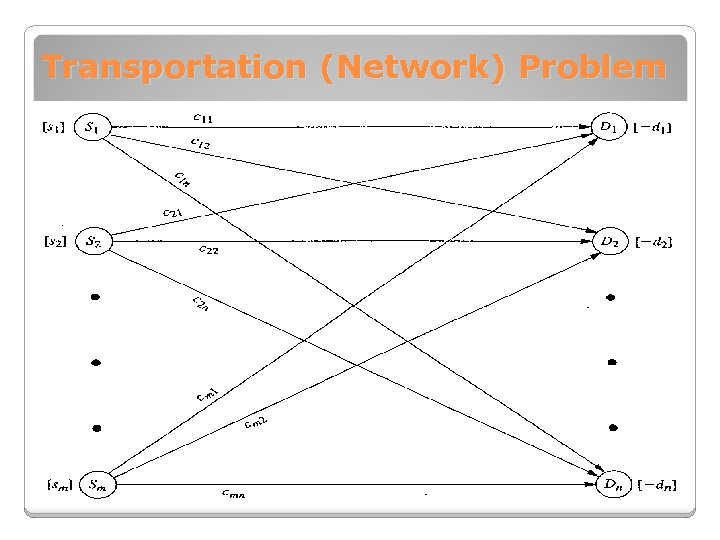Transportation (Network) Problem

Requirement Assumption

Feasible Solutions Property

Cost Assumption

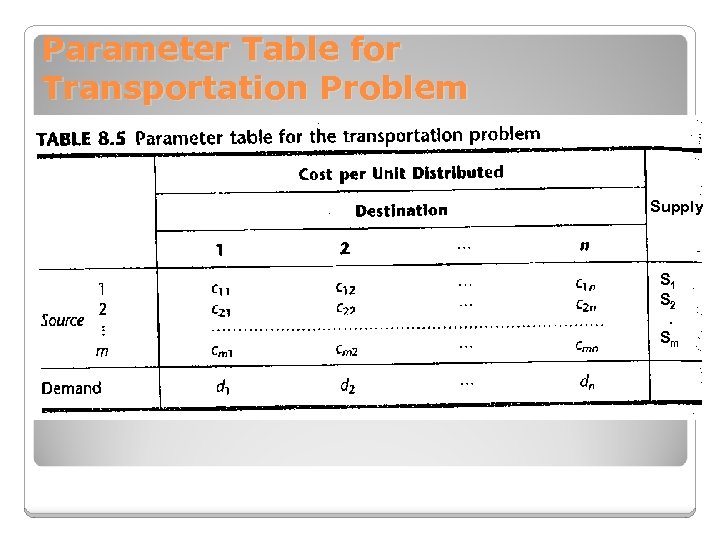Parameter Table for Transportation Problem Supply S 1 S 2. Sm

Transportation Problem Modeling Any problems (whether involving transportation or not) fits the model for a transportation problem if it can be described completely in term of a parameter table like Table 8. 5 and it satisfies both the requirements assumption and cost assumption. The objective is to minimize the total cost of distributing the units. All the parameters of the model are included in this parameter table.

Objective Function & Constraints

Software for Solving LP Programs 1. Lingo: to download software and access user menu at http: //www. lindo. com/index. php? option=com_content&view= article&id=34&Itemid=15 2. Excel with Add-ins

Solving LP Models with Lingo – Download software for free

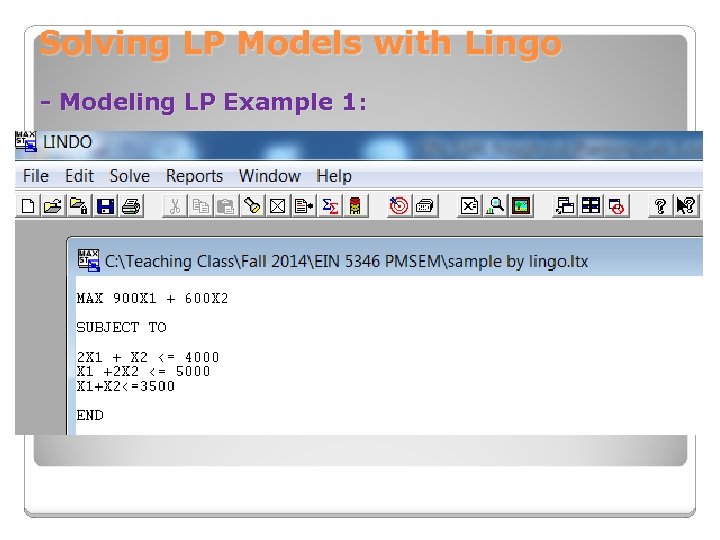Solving LP Models with Lingo - Modeling LP Example 1:

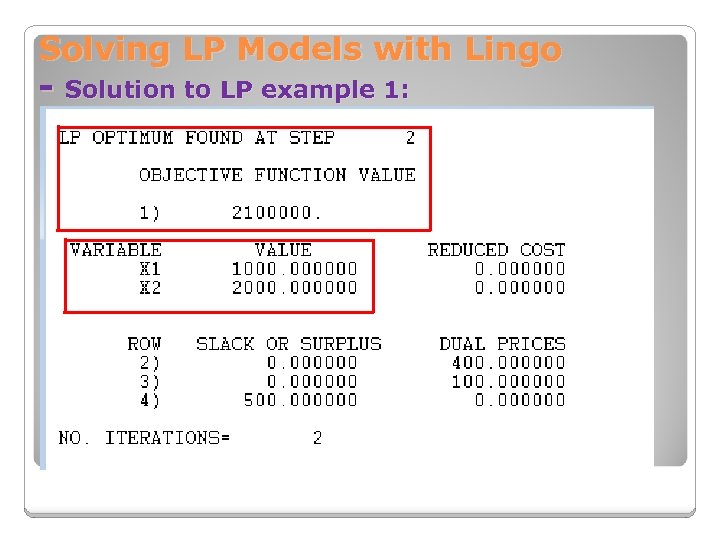Solving LP Models with Lingo - Solution to LP example 1:

Solving LP Models with Excel - to include Solver Addin

Solving LP Models with Excel - Solver Addin included

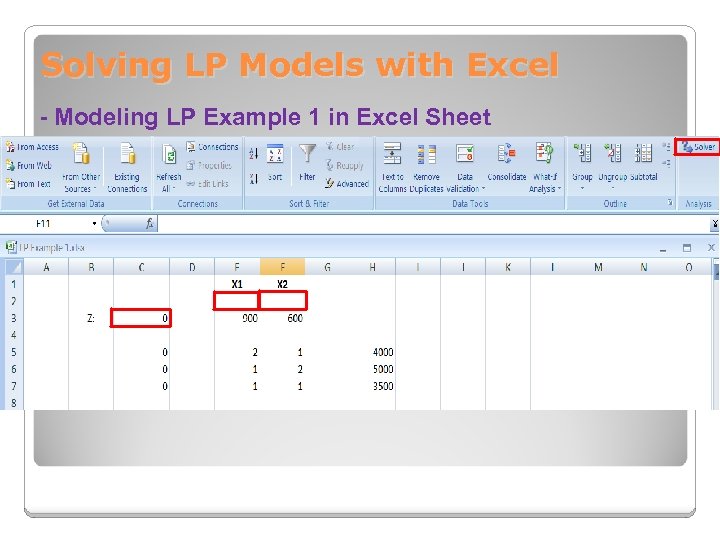Solving LP Models with Excel - Modeling LP Example 1 in Excel Sheet

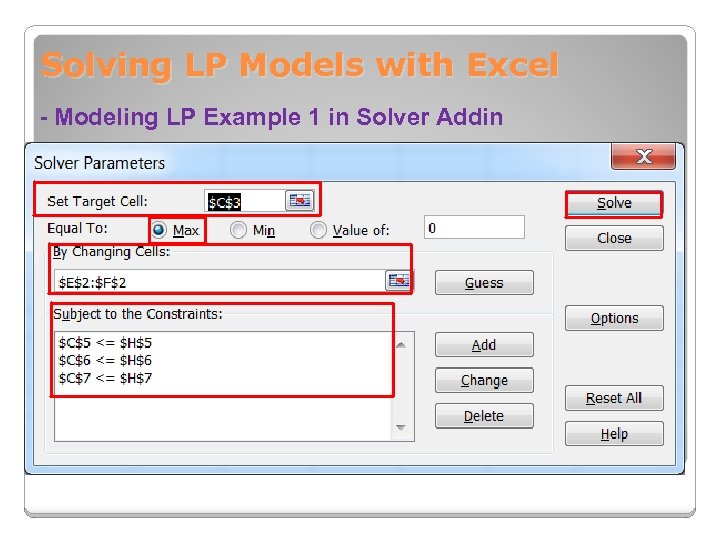Solving LP Models with Excel - Modeling LP Example 1 in Solver Addin

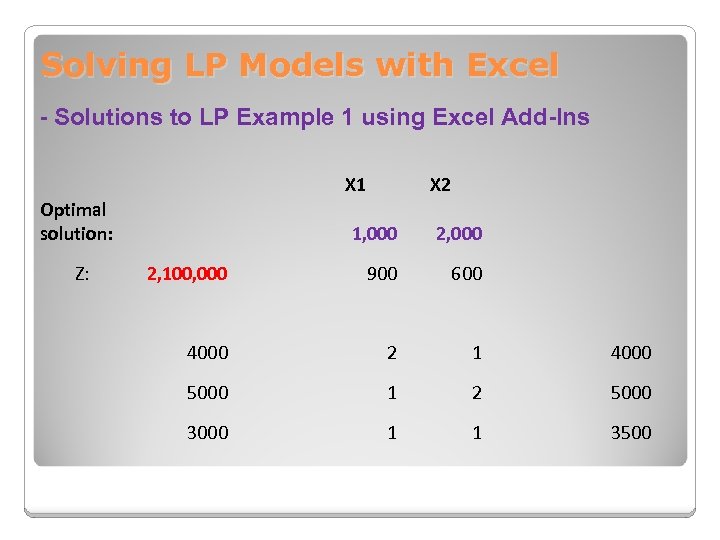Solving LP Models with Excel - Solutions to LP Example 1 using Excel Add-Ins X 1 Optimal solution: Z: X 2 1, 000 2, 100, 000 900 600 4000 2 1 4000 5000 1 2 5000 3000 1 1 3500

Lab 6: Exercises: (Due date: 10/16/17) Questions 1 and 2 by team, Questions 3 and 4 for LP problem by individual. 1. Ex 1: Create demands from distribution centers 2. Ex 2. Network Planning with Multilevel Heuristic

Questions 3 and 4 by individual 3. Please solve the following LP problem. Objective: Min Z = 10, 000 X 1 + 15, 000 X 2 S. T. X 1 + 2 X 2 >= 4 X 1+ X 2 >= 2. 5 X 1, X 2 >= 0 1) Draw a graph 2) Plot the constraint function 3) Outline the feasible solution 4) Circle the optimal solution point.

Questions 3 and 4 by individual 4. The Green Up Fertilizer Company ships fertilizer from three manufacturing plants to four distribution centers (DC). The shipping cost per truckload of fertilizer from each plant to each DC is: Plant Distribution Center (DC) A 1 2 3 B C D $464 $352 $995 $513 $416 $682 $654 $690 $388 $867 $791 $685 Plant 1 has a monthly capacity of 75 truckload, Plant 2 has a monthly capacity of 125 truckload, and the Plant 3 has a monthly capacity of 100 truckload. The monthly DC demand is A = 80 truckload, B = 65 truckload, C = 70 truckload, and D = 85 truckload. Please formulate an LP problem to determine how much truckload of fertilizer should be shipped from each plant to each DC per month to minimize monthly shipping cost. 1) Define the objective. 2) Define the decision variables. 3) Write the mathematical function for the objective. 4) Write the constraints. 5) Solve the LP problem using Lingo or Excel Addin.