РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ Программно-методическая разработка по теме: «Оптимизация игровых ситуаций» Выполнили студенты ГУБ-22: Ташбулатов Бактияр Дабо Мариама Денисова Надежда Москва 2013
Общая формулировка: Игровые модели применяются для принятия решения в ситуациях полной неопределенности, которые характеризуются наличием заинтересованных сторон, наборами возможных действий каждой стороны, четко сформулированными интересами сторон. Вероятностная стратегическая игра с конечными множествами возможных действий игроков и полной информацией, в которой участвуют две стороны, имеющие противоположные интересы, называется конечной (матричной) игрой двух лиц с нулевой суммой. Пример формулировки : Фирма готовится провести диверсификацию производства. В дополнение к отработанным моделям ею разработаны еще три изделия. Перспективными покупателями продукции могут являться рекламные компании, PR-компании, детские учреждения и фирмы-организаторы празднований. Маркетологи рассчитали прогнозные цены, по которым каждая группа покупателей готова приобретать изделия. Требуется определить структуру выпуска продукции, обеспечивающую максимальный доход фирмы. Одновременно менеджеры фирмы должны необходимо найти оптимальную стратегию противоположной стороны – покупателей, определяемую как расчетную долю затрат каждой группы покупателей в общей сумме расходов на товары фирмы, что позволит правильно определить приоритеты.
• Математическая модель. В рассматриваемой ситуации необходимо провести анализ стратегий участников рынка с двух позиций – со стороны фирмы и с противоположной стороны – с точки зрения покупателей продукции. Вся необходимая для этого информация содержится в результатах маркетинга. Это платежная матрица С, элементы которой показывают, какую цену готова платить каждая группа покупателей за каждое изделие фирмы. • Целью фирмы-производителя является такой выбор стратегий, который обеспечивает максимальную цену игры ν. Целевая функция задачи имеет вид • ν max • Система ограничений задачи строится, исходя из предположения о том, что оптимальная стратегия производителя должна обеспечивать ему получение дохода не меньше, чем цена игры ν, для любой группы потребителей. То есть при любой стратегии противной стороны (рынка) фирма должна получить доход не ниже величины цены игры.
Рассмотрим группу потребителей RJ. Цены, по которым эта группа готова покупать предлагаемые изделия, образуют J столбец платежной матрицы С. Для стратегии производителя, описываемой вектором структуры производства P={P 1, P 2, P 3, P 4, P 5}, расходы DIJ рассматриваемой группы на модель GI будут равны произведению платежа CIJ на долю объема производства PI: DIJ=CIJ*PIJ. Общая величина расходов данного сектора рынка на продукцию фирмы будет представлять собой сумму затрат на все модели. Условие оптимального выбора структуры производства – компонент вектора P – предполагает, что для любого сектора рынка расходы должны быть не ниже цены игры ν. То есть для любой группы потребителей должно выполняться неравенство DJ≥ ν , откуда следует, что в систему ограничений должны входить N неравенств
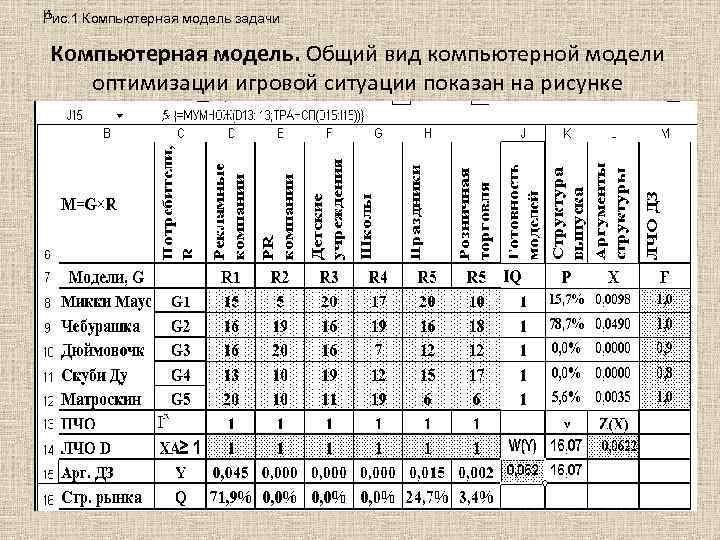
и Рис. 1 Компьютерная модель задачи Компьютерная модель. Общий вид компьютерной модели оптимизации игровой ситуации показан на рисунке
Настройки программы "Поиск решения"
• Компьютерная технология моделирования и исследования игровой ситуации включает в себя следующие операции: 1)Разместить исходные данные – матрицу платежей С[D 8: I 12], вектор готовности продукции IG[G 8: G 12] и вектор-индикатор потребителей IR[D 3: I 13]. 2)Отвести блоки ячеек для размещения вектора решения Х[L 8: L 12]. 3)Отвести ячейку для размещения целевого функционала Z(X)[L 14] и ввести в нее формулу =МУМНОЖ(ТРАНСП(L 8: L 12); J 8: J 12). 4)В ячейку цены игры ν[K 14] ввести формулу =1/L 14. 5)Вычислить вектор структуры выпуска Р[K 8: K 12] по =K 14*L 8: L 12. 6)Отвести блок ячеек для вычисления левых частей плановых ограничений D=ХС[D 14: I 14] по формуле =МУМНОЖ(ТРАНСП(L 8: L 12); D 8: I 12) 7)Настроить и запустить программу «Поиск решения» .
Ответ: • В результате вычислений при помощи представленной компьютерной модели исследуемой игровой ситуации получено решение – структура плана выпуска продукции, обеспечивающего максимальную цену игры производителя при любой стратегии покупателей. В соответствии с данным решением план должен предусматривать выпуск ММ в количестве 15, 7% от общего объема производства, Ч – 78, 7%, остальные 5, 6% - М. В условиях, представленных результатами маркетинговых исследований, план не должен включать изделия Д и СД. Такая структура выпуска гарантирует, что расходы каждой группы покупателей на продукцию фирмы будут не меньше оптимальной цены игры, равной в данном случае 16, 07. Одновременно анализ оптимальных стратегий противной стороны рыночных отношений – покупателей показывает, что основной объем покупок будет приходиться на долю рекламных компаний (71, 9%); заметна также доля продаж в секторе организаторов праздников (24, 7%); незначительный объем потенциального рынка составляет розница (3, 4%); остальные сегменты рынка неперспективны.
Спасибо за внимание! Дабо Мариама Денисова Надежда Ташбулатов Бахтияр ГУБ-22
Скачать презентацию РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ Программно-методическая разработка по теме
Оптимизация игровых ситуации.pptx