Клеточные автоматы.pptx
- Количество слайдов: 24

РОССИЙСКИЙ УНИВЕРСИТЕТ ДРУЖБЫ НАРОДОВ К ЛЕТОЧНЫЕ АВТОМАТЫ Выполнила: Поджарая Анастасия Сергеевна студентка группы НИ-301

ЧТО ТАКОЕ КЛЕТОЧНЫЙ АВТОМАТ? Кле точный автомат (КА) — набор клеток, образующих некоторую периодическую решетку с заданными правилами перехода, определяющими состояние клетки в следующий момент времени через состояние клеток, находящимися от нее на расстоянии не больше некоторого, в текущий момент времени. Идея возникла в конце сороковых годов 20 века, и принадлежит Джону фон Нейману и Конраду Цусе.

ОСНОВНЫЕ ПОНЯТИЯ Состояние решётки - совокупность состояний всех клеток решётки называется. Правило клеточного автомата (или закон системы) – закон, в соответствии с которым меняется состояние решётки. Итерация - каждое изменение состояния решётки. Время в рассматриваемой модели дискретно и каждая итерация соответствует некому моменту времени. Окрестность клетки(соседи клетки) - множество клеток, влияющих на значение данной, за исключением её самой.
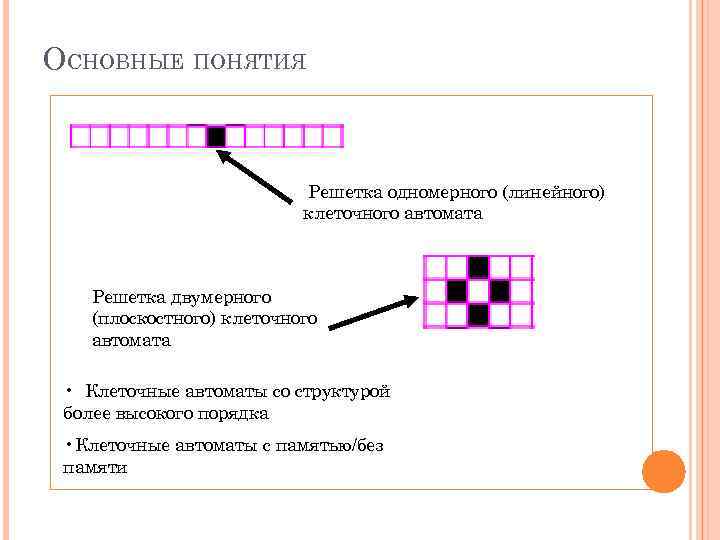
ОСНОВНЫЕ ПОНЯТИЯ Решетка одномерного (линейного) клеточного автомата Решетка двумерного (плоскостного) клеточного автомата • Клеточные автоматы со структурой более высокого порядка • Клеточные автоматы с памятью/без памяти

ОСНОВНЫЕ СВОЙСТВА КА Значения во всех клетках меняются единовременно. В конце итерации, а не по мере вычисления. Локальность правил. На новое состояние клетки могут влиять только элементы её окрестности и, возможно, она сама. Чтобы узнать, что произойдет мгновенье спустя, достаточно посмотреть на ближайшее окружение: никакое дальнодействие не допускается. Однородность ( «Одинаковость» ) системы. Ни одна область решётки не может быть отличена от другой по каким-либо особенностям правил и т. п. Множество возможных состояний клетки - конечно. Это условие необходимо, чтобы для получения нового состояния клетки требовалось конечное число операций.
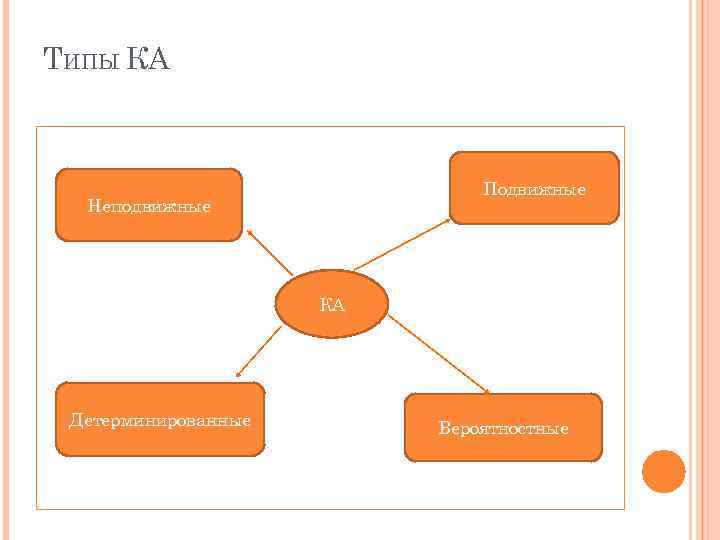
ТИПЫ КА Подвижные Неподвижные КА Детерминированные Вероятностные

ДЕТЕРМИНИРОВАННЫЕ, ПОДВИЖНЫЕ И НЕПОДВИЖНЫЕ КА В детерминированных КА состояние ячейки i+1 в последующий момент времени однозначно определяется состоянием этой ячейки и ее ближайших соседей в предыдущий момент времени. Подвижные КА характеризуются возможностью изменения положения клетки в решетке во время эволюции системы В неподвижных КА положение клетки во время эволюции остается постоянным.

ВЕРОЯТНОСТНЫЕ КА КА, в которых состояния ячеек в последующий момент времени определяются на основе некоторых вероятностей, называются вероятностными КА (ВКА). В классических ВКА правила переходов имеют абстрактный характер и не связаны однозначно с реальными процессами, происходящими в моделируемой системе.

КЛАССИФИКАЦИЯ КА ПО ТИПАМ ПОВЕДЕНИЯ Класс 1. Автоматы, приходящие через определенное время к устойчивому однородному состоянию Класс 2. Автоматы, которые через некоторое время после запуска генерируют стационарные или периодические во времени состояния. Класс 3. Автоматы, в которых по прошествии некоторого времени перестаёт наблюдаться корреляция процесса с начальными условиями. Класс 4. Поведение определяется начальными условиями. С их помощью можно генерировать весьма сложные шаблоны поведения

ПРИМЕНЕНИЕ КА Составление генетических алгоритмов Поиск кратчайшего пути на графе Моделирование распространения тепловых потоков Моделирование описания движения толпы Моделирование развития популяции вида Моделирование взаимодействия видов по типу «хищник – жертва» Моделирование многих других химических, физических и биологических процессов

ОБЩИЕ ПРАВИЛА ПОСТРОЕНИЯКА Состояние клеток дискретно (обычно 0 и 1, хотя могут быть автоматы и с большим числом состояний). Соседями являются ограниченное число клеток, часто это ближайшие клетки. ( по фон Нейману – соседи граничат по граням, по Муру – также и по диагоналям) Правила, задающие динамику развития клеточного автомата, обычно имеют простую функциональную форму и зависят от решаемой проблемы. Клеточный автомат является тактируемой системой, т. е. смена состояний клеток происходит одновременно.

РЕАЛИЗАЦИЯ КЛЕТОЧНОГО АВТОМАТА Вводятся два массива для хранения состояний клеток Определяется функция переходов клетки решетки На нулевом шаге производится заполнение решетки (первого массива) начальными данными Для вычисления новых состояний вводится цикл После завершения итерации значения из всех элементов второго массива переносятся в первый массив

ПРИМЕРЫ КА Игра «Жизнь» Игра «Аква-Тор» Линейный автомат Автомат, моделирующий движение толпы Тьюрмиты Автоматы серии «Поколения»

АВТОМАТЫ СЕРИИ « ОКОЛЕНИЯ» П Автоматы с числом состояний более чем два. Правила изменений состояния клетки записываются следующим образом S/B/C где: S - набор цифр от 0 до 8, определяет число "живых" соседей, при котором клетка остается "в живых", B - набор цифр от 0 до 8, определяет число "живых" соседей при котором "мертвая" клетка становится "живой" С - число, определяет число ходов "умирания" клетки
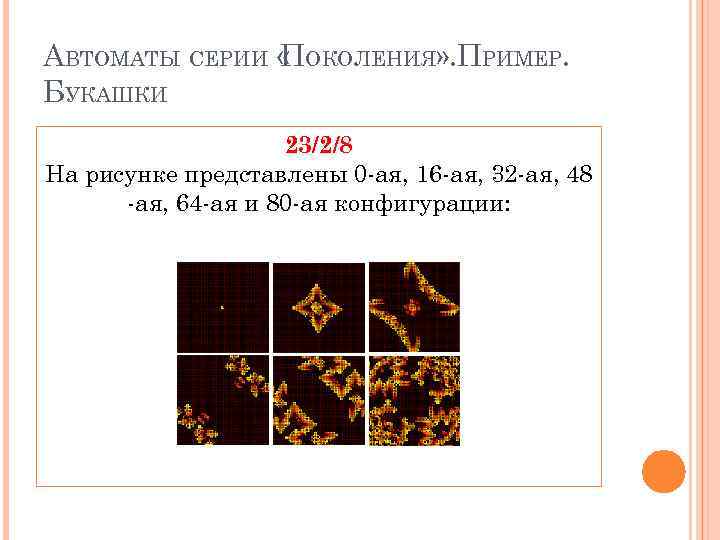
АВТОМАТЫ СЕРИИ « ОКОЛЕНИЯ» . ПРИМЕР. П БУКАШКИ 23/2/8 На рисунке представлены 0 -ая, 16 -ая, 32 -ая, 48 -ая, 64 -ая и 80 -ая конфигурации:

ИГРА « ИЗНЬ» Ж 1. 2. 3. Создана игра «Жизнь» была в 1970 году Джоном Хортоном Конуэем, математиком Кембриджского университета. Правила игры «Жизнь» : Выживание. Каждая клетка, имеющая две или три соседние живые клетки, выживает и переходит в следующее поколение. Гибель. Каждая клетка, у которой больше трёх соседей, погибает из-за перенаселённости. Каждая клетка, вокруг которой свободны все соседние клетки или же занята всего одна клетка, погибает от одиночества. Рождение. Если число занятых клеток, с которыми граничит какая-нибудь пустая клетка, в точности равно трём, то на этой клетке происходит рождение нового организма.

СТРУКТУРЫ, РЕАЛИЗУЮЩИЕСЯ В ИГРЕ «ЖИЗНЬ» Вскоре после опубликования правил, было обнаружено несколько интересных шаблонов (вариантов расстановки живых клеток в первом поколении): Устойчивые фигуры: фигуры, которые остаются неизменными Периодические фигуры: фигуры, у которых состояние повторяется через некоторое число поколений Двигающиеся фигуры: фигуры, у которых состояние повторяется, но с некоторым смещением Ружья: фигуры, у которых состояние повторяется, но дополнительно появляется двигающаяся фигура Паровозы: двигающиеся фигуры, которые оставляют за собой следы в виде устойчивых или периодических фигур Пожиратели: устойчивые фигуры, которые могут пережить столкновения с некоторыми двигающимися фигурами
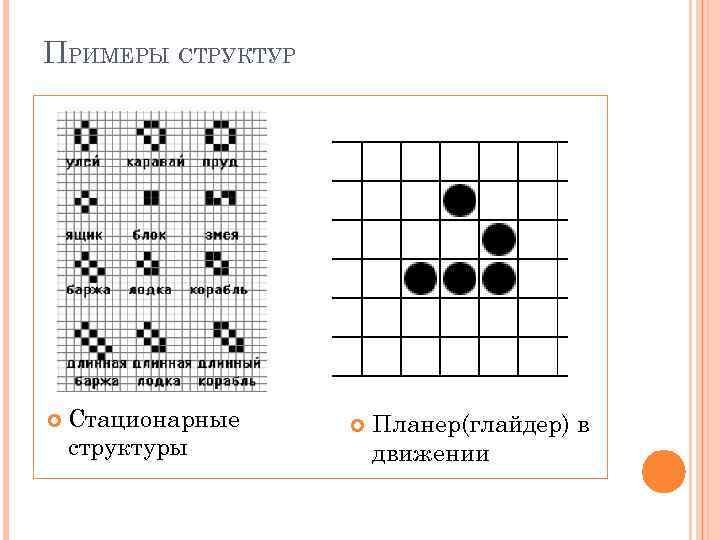
ПРИМЕРЫ СТРУКТУР Стационарные структуры Планер(глайдер) в движении

ЭДЕМ Райским садом называется такое расположение клеток, у которого не может быть предыдущего поколения. Практически для любой игры, состояние клеток в которой определяется несколькими соседями на предыдущем шаге, можно доказать существование садов Эдема, но построить конкретную фигуру гораздо сложнее.

ИГРА « КВА-ТОР» А Игра «Аква-Тор» – наглядный пример применения клеточных автоматов в биологии. Игра моделирует поведение системы, состоящей из двух популяций, условно называемых «травоядные» и «хищники» . Пищей для «хищников» являются особи «травоядных» , пищи же для «травоядных» бесконечно много. Полем для игры является тор– квадрат, замкнутый сам на себе, т. е. если особь достигает крайней клетки квадрата, она переносится на противоположную сторону квадрата автоматически.

ИГРА « КВА-ТОР» А Параметры системы: особь может переместиться на любую клетку, имеющую с данной общую сторону. Направление выбирается случайно из возможных свободных. особь может оставить потомство в той клетке, из которой она переместилась. Потомство появляется периодически, период является параметром. если особь является «хищной» , то она может поглотить свою жертву, при этом перемещаясь на место жертвы. особь живет ограниченное количество времени, называемое временем жизни особи – так же параметр. если «хищная» особь не находит себе пищи в течение определенного времени (называемого временем голодной смерти), то она погибает. Время голоднойсмерти является параметром.

ТЬЮРМИТЫ Тьюрмит - это некий синтез клеточного автомата и машины Тьюринга. От клеточного автомата тьюрмит отличается тем, что в начальный момент времени его поле пусто и какая-то одна клетка считается начальной (тьюрмит занимает начальную позицию, находится в начальном состоянии, начальное направление, например, на восток). Затем на каждом такте применяется правило вида: <текущее состояние><старый цвет текущей клетки><новый цвет><направление перемещения><новое состояние>

ТЬЮРМИТЫ Состояния принято обозначать латинскими буквами; цвета - числами от 0 до 15 (16 -ти цветовая палитра), направление перемещения изменяется относительно текущего курса тьюрмита, обозначается числами -1 (повернуть налево), 1 (повернуть направо), 0 (прямо). Например, правило А 0 15 0 В означает, что если тьюрмит находится в состоянии А и стоит на черной клетке, то он должен покрасить ее в белый цвет, продвинуться на одну клетку в текущем направлении и перейти в состояние В.
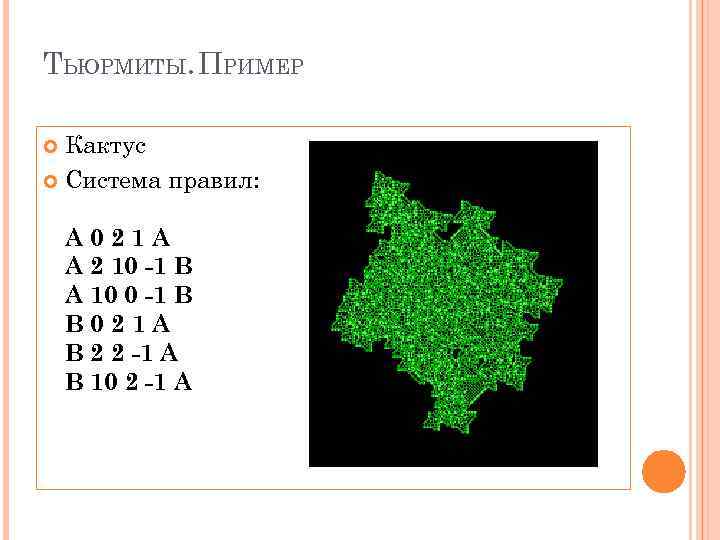
ТЬЮРМИТЫ. ПРИМЕР Кактус Система правил: A 021 A A 2 10 -1 B A 10 0 -1 B B 021 A B 2 2 -1 A B 10 2 -1 A
Клеточные автоматы.pptx