ROGICS 08 May 14 2008 Universal Random Semi-Directed

ROGICS’ 08 May 14, 2008 Universal Random Semi-Directed Graphs Anthony Bonato Wilfrid Laurier University Ryerson University Canada Joint work with Dejan Delić and Changping Wang Random Semi-Directed Graphs. Anthony Bonato

Web graph Random Semi-Directed Graphs. Anthony Bonato 2

The web graph • nodes: web pages • edges: links Random Semi-Directed Graphs. Anthony Bonato 3

How big is the web? • the web is infinite… – calendars, online organizers – random strings: • google “raingod random strings” • total web ≈ 54 billion static pages (Hirate, Kato, Yamana, 07) Random Semi-Directed Graphs. Anthony Bonato 4

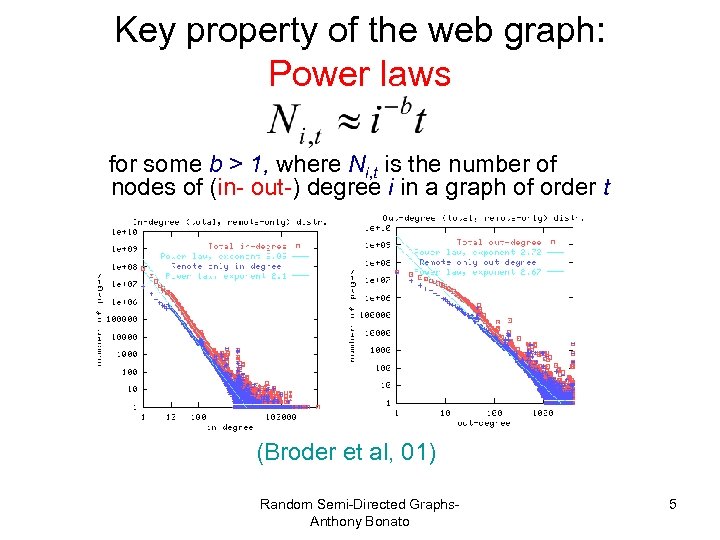Key property of the web graph: Power laws for some b > 1, where Ni, t is the number of nodes of (in- out-) degree i in a graph of order t (Broder et al, 01) Random Semi-Directed Graphs. Anthony Bonato 5

Other properties of the web graph • small world property (Watts, Strogatz, 98): – in a graph of order t, diameter O(log t), average distance: O(loglog t) – globally sparse, locally dense • many bipartite subgraphs, sparse cuts, strong conductance, eigenvalue power law, … Random Semi-Directed Graphs. Anthony Bonato 6

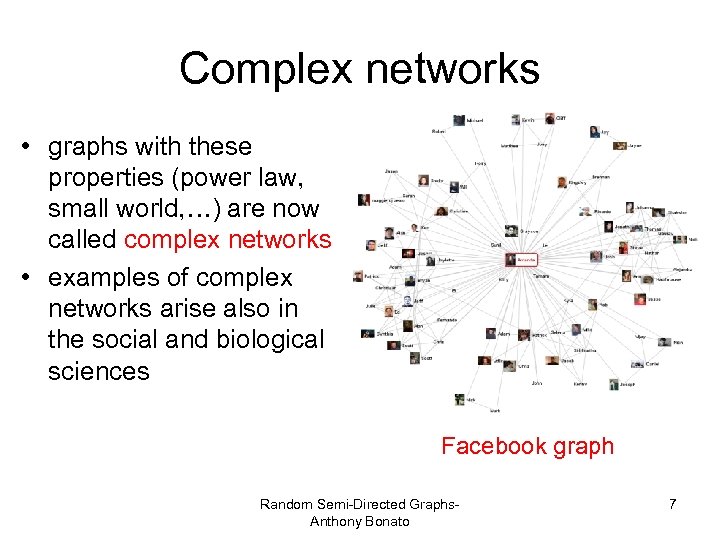Complex networks • graphs with these properties (power law, small world, …) are now called complex networks • examples of complex networks arise also in the social and biological sciences Facebook graph Random Semi-Directed Graphs. Anthony Bonato 7

Preferential attachment (PA) model for complex networks (Barabási, Albert, 99), (Bollobás, Riordan, Spencer, Tusnady, 01) • parameter: m a positive integer • at time 0, add a single directed edge • at time t+1, add m directed edges from a new node vt+1 to existing nodes – the edge vt+1 vs is added with probability Random Semi-Directed Graphs. Anthony Bonato 8

Properties of the PA model • (BRST, 01) For integers m > 0, a. a. s. (that is, with probability tending to 1 as t→∞) for all k satisfying 0 ≤ k ≤ t 1/15 • (Bollobás, Riordan, 04) For integers m > 0, a. a. s. the diameter of the graph at time t is Random Semi-Directed Graphs. Anthony Bonato 9

• several web graph models introduced and rigorously analyzed – Bollobás, Chung, Frieze, Kleinberg, Luczak, … • in most models, nodes are born joined to an -set of vertices satisfying some properties m – high degree – in a neighbour set – older nodes Random Semi-Directed Graphs. Anthony Bonato 10

Semi-directed graphs • • the following assumptions are common to most models of the web graph and complex networks 1. on-line: nodes are added over a countable sequence of discrete time-steps 2. constant out-degree: new vertices point only to existing ones, and for a fixed integer m > 0, there are exactly m such directed edges a digraph satisfying 1) and 2) is called semi-directed – name recently coined by Bollobás – emphasizes that orientation arises according to time: “new point to old” Random Semi-Directed Graphs. Anthony Bonato 11

• semi-directed graphs lead naturally to countably infinite limits: – unions of chains of finite semi-directed graphs • are the limits unique? • do the limits naturally arise from a random graph process? • what properties do the limits satisfy? Random Semi-Directed Graphs. Anthony Bonato 12

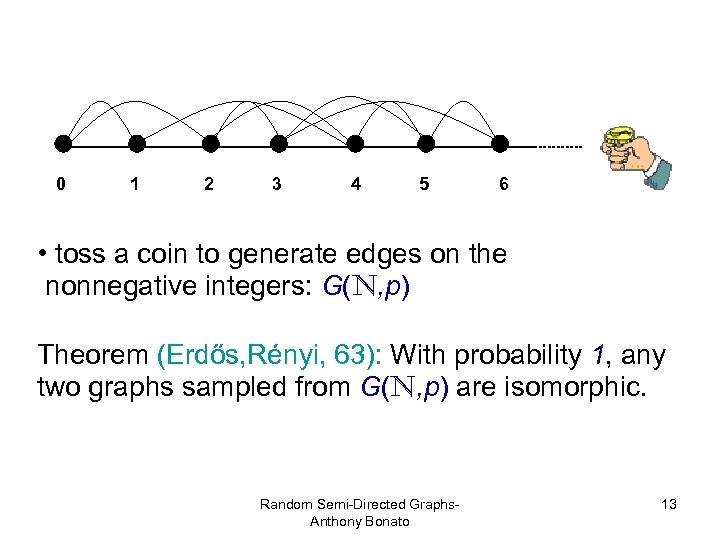0 1 2 3 4 5 6 • toss a coin to generate edges on the nonnegative integers: G(N, p) Theorem (Erdős, Rényi, 63): With probability 1, any two graphs sampled from G(N, p) are isomorphic. Random Semi-Directed Graphs. Anthony Bonato 13

The infinite random graph • unique isomorphism type, R – infinite random graph, Rado graph – existentially closed (e. c. ): A B z • R is the unique countable e. c. graph • Fraïssé: R is the unique universal homogeneous graph Random Semi-Directed Graphs. Anthony Bonato 14

Rm, H • fix R 0 = H a finite digraph with m vertices • suppose Rt is defined • to form Rt+1, for each m-set S in Rt, add a vertex zs joined to each vertex of S and to no other vertices of Rt Rt S zs • the limit graph is Rm, H Random Semi-Directed Graphs. Anthony Bonato 15

Properties of Rm, H • acyclic; constant out-degree m, sensitive to H • unlike R, Rm, H is not inexhaustible: S – deleting vertices changes constant out-degree zs Random Semi-Directed Graphs. Anthony Bonato 16

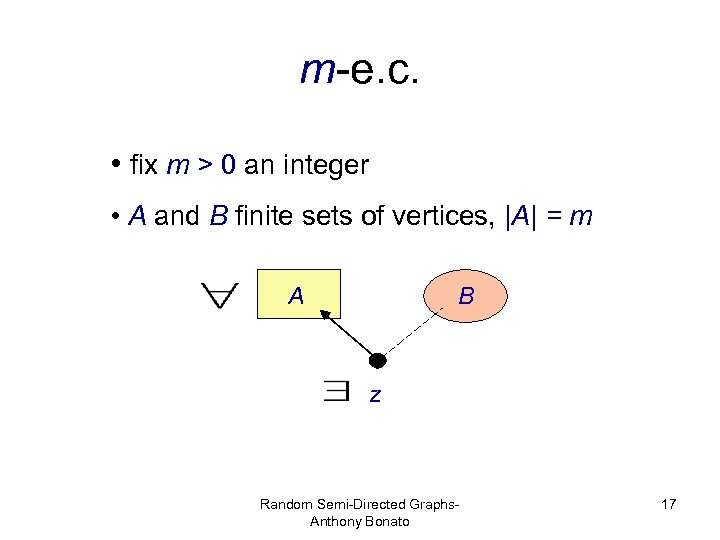m-e. c. • fix m > 0 an integer • A and B finite sets of vertices, |A| = m B A z Random Semi-Directed Graphs. Anthony Bonato 17

Uniqueness and universality Theorem (Bonato, Delić, Wang, 08) A countable digraph G is isomorphic to Rm, H iff G is semi-directed with initial graph H, and satisfies the m-e. c. property. • proved by a back-and-forth argument • corollary: each countable semi-directed digraph embeds in Rm, H Random Semi-Directed Graphs. Anthony Bonato 18

Age Dependent Process (ADP) Random Semi-Directed Graphs. Anthony Bonato 19

Universal random semi-directed graphs Theorem (BDW, 08) With probability 1, a countable digraph generated by ADP with parameters m and H is isomorphic to Rm, H. Random Semi-Directed Graphs. Anthony Bonato 20

Generalization • theory may be generalized so that the isotypes induced by out-neighbour sets are in a specified infinite hereditary class of finite digraphs: – all digraphs – tournaments; linear orders – digraphs with bounded in-degree… Random Semi-Directed Graphs. Anthony Bonato 21

Group of R • R is homogeneous (eg vertex- and edge-transitive) • R has a rich automorphism group (see P. Cameron’s surveys) – cardinality and is simple – cyclic automorphisms – strong small index property – embeds all countable groups Random Semi-Directed Graphs. Anthony Bonato 22

Group of Rm, H • Rm, H is not vertex-transitive Theorem (BDW, 08) Aut(Rm, H) embeds all countable groups. • implies that Aut(Rm, H): – generates the variety of all groups – has undecidable universal theory Random Semi-Directed Graphs. Anthony Bonato 23

Future research • further investigate the automorphism group and endomorphism monoid of Rm, H – distinguishing number is 2 • consider limits of other recent models of complex networks – (Kleinberg, 05): limits of PA model – (Bonato, Janssen, 04/08): limits of copying model… – geometric models? Chung, Frieze, Bonato et al. Random Semi-Directed Graphs. Anthony Bonato 24

• preprints, contact: Google: “Anthony Bonato” Random Semi-Directed Graphs. Anthony Bonato 25

New book Random Semi-Directed Graphs. Anthony Bonato 26