Robust Mechanisms for Information Elicitation Aviv Zohar

Robust Mechanisms for Information Elicitation Aviv Zohar & Jeffrey S. Rosenschein

Overview of the talk • • • Motivation – how to pay for information Scoring Rules Mechanisms for information elicitation Robust mechanisms for a single agent Multi-agent extensions Conclusion

Motivation - How to Pay for Information • Alice wishes to know the weather in Tel. Aviv – This cannot be predicted in advance by anyone! • She’s only interested in the chance of rain. • There are two options:

Paying for Information • Bob lives in Tel-Aviv. • He can go outside and check the weather. • Getting the information costs him some effort. A cost of c. • He wants Alice to pay him for his efforts.

Paying for Information • If Alice pays him c$ no matter what he says he can just make something up. • If Alice pays him c 1$ for saying rain, and c 2$ for saying clear weather, he will pick the larger payment every time. • Conclusion: Alice has to have some way to verify the information. • Example: The weather in Jerusalem is correlated with the weather in Tel-Aviv • In the real world we often buy unverified information. We are usually playing a repeated game.

How to Pay for Information • Bob knows that Tel-Aviv is usually sunny. • His beliefs affect the cost-benefit analysis. • Alice needs to take Bob’s beliefs into consideration when deciding on payments. • Does she know what Bob believes? Usually only approximately! • Can she find a payment scheme to Bob that will be robust against small changes in belief?

Information Elicitation vs. Preference Elicitation. • Information Elicitation: – – Knowledge is changing hands. The seller only cares about payment. Not interested in how the knowledge is to be used. The buyer wants the truth! • Preference Elicitation: – Information is just the means to an end: Achieving some optimal outcome. – The outcome is the bottom line. – The mechanism has more freedom of action – can control outcome as well as payments. (EXAMPLE: Auctions)

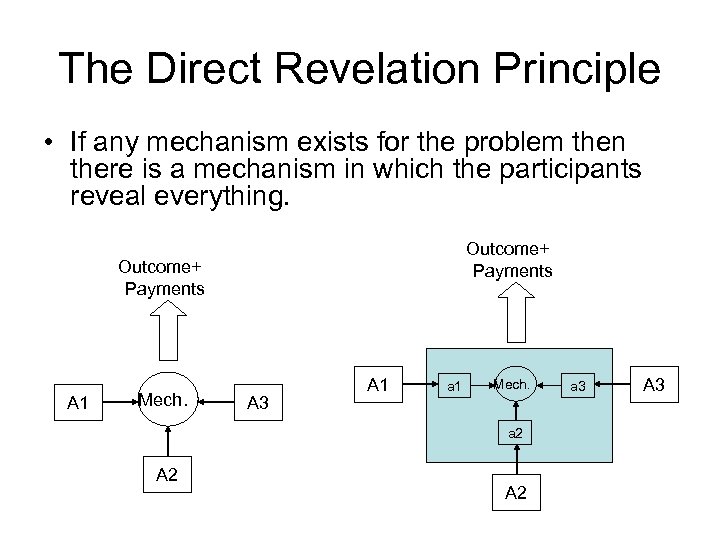
The Direct Revelation Principle • If any mechanism exists for the problem then there is a mechanism in which the participants reveal everything. Outcome+ Payments A 1 Mech. A 3 A 1 a 1 Mech. a 2 A 2 a 3 A 3

Direct Revelation • Direct revelation can allow us to get over the problem of learning bob’s beliefs. • We can ask Bob to reveal everything: – The information to be sold – His beliefs about probabilities. • But… – We don’t want to reveal everything. – Information is what Bob sells! – No trusted third party.

Proper Scoring Rules • A way to evaluate a probabilistic prediction. • For a prediction p, and a final outcome o we shall pay: S(p, o). • A proper scoring rule is one in which telling a more accurate prediction gives a higer payment: • Eo~p[S(p, o)] > Eo~p[S(q, o)]

Scoring Rules • Eo~p[S(p, o)] > Eo~p[S(q, o)] • There are lots of functions S(. , . ) that fulfill this condition. • Example: Logarithmic payments: S(p, i) = log(pi) In which case:

Scoring Rules • Predictions are given in the form of probability distributions. • How do we combine the predictions of two different experts that have access to different sources of information? • We need a model of how their information interacts.

Our Model • Seller i owns a random variable Xi that it pays ci to discover. • Buyer owns a random variable Ω • After it learns about values x’ from the sellers and a value ω, it pays the sellers uiω, x’ • The variables X 1, X 2, …, Ω are presumably not independent • We assume that they are governed by probability distribution px 1, x 2, …, ω • Now we know how to combine information from several sources. Pr(ω|X 1, X 2…)

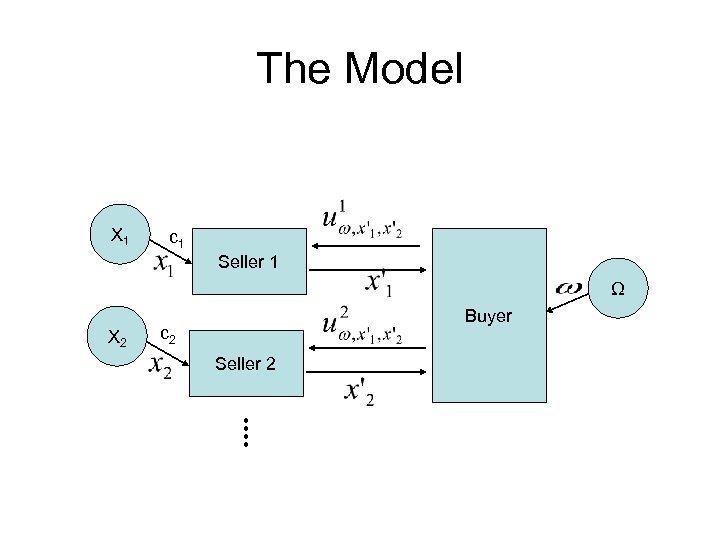
The Model X 1 c 1 Seller 1 Ω X 2 Buyer c 2 Seller 2

The Requirements from a Proper Mechanism (Single Agent) 1. Truth-telling: The truth is more profitable than any lie. 2. Investment: Knowing is better than guessing. 3. Individual Rationality: There is a positive expected gain from participating.

Finding a Mechanism • We assume P is known. • The constraints are all linear in the payments u. • We can find a payment scheme using some LP solver. • We can optimize the cost too: • When can we find a good mechanism? • What is the optimal cost?

The Truth is Enough • Suppose we have some set of payments that satisfies the truthfulness constraints: • We can scale and shift it To satisfy the other constraints.

The Truthfulness Constraints • Let’s define: • Now we get: • And also: • We need every pair of vectors px, px’ to be linearly separated by vx, x’

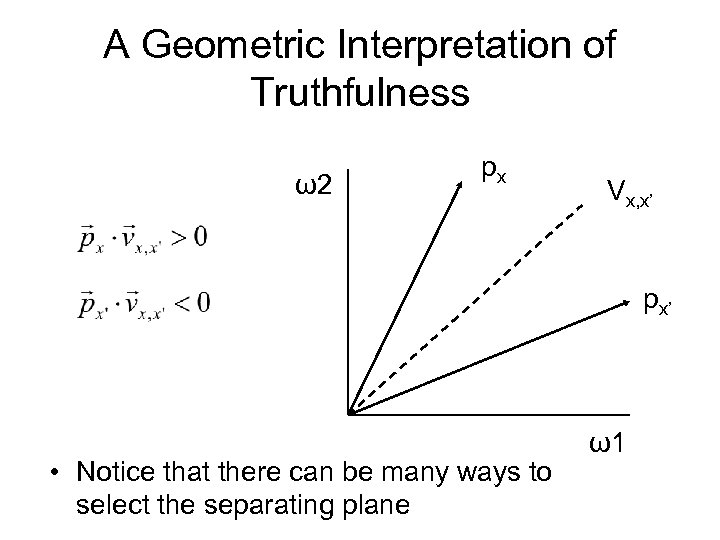
A Geometric Interpretation of Truthfulness ω2 px Vx, x’ px’ • Notice that there can be many ways to select the separating plane ω1

Existence of a Mechanism • A mechanism exists if and only if all vectors px are pair-wise independent. – One direction is easy: we can’t separate vectors that are linearly dependent. – For the other direction: show a working mechanism: – Setting does the trick.

Robust Mechanisms • We return to the case where P is not known exactly. • We assume ε is small (according to L∞). • certain solutions may be better than others ω2 px px’ ω1

Robustness of a Specific Payment Scheme • A conservative definition: A payment scheme u will be considered ε-robust with regard to distribution if it is proper for every distribution for which • How do we find the robustness level of a payment scheme? – Find the minimal ε for which a constraint is violated.

Robustness of a Payment Scheme • The robustness of one of the truthfulness constraints can be found by solving: • After solving a similar program for every constraint, take the smallest ε found.

Finding a Robust solution • Given an ε, all ε-robust solutions form a convex set. • This is a stochastic programming problem. – Find a solution to a mathematical program with uncertainty regarding the constraints. • The ellipsoid algorithm needs only a separation oracle in order to optimize over the set of solutions. • A separation oracle provides a linear separator between any non-solution and the set of solutions. • We’ve just seen how to find one! Find a constraint that the payments + a perturbation violate.

The full stochastic program:

Robust Mechanisms • Definition: The robustness level of a problem p is the largest ε that can be set as the robustness of a solution. • How can we find it? • Use binary search. – The robustness level is somewhere between 0 and 1. – Test at any wanted ε in between by trying to actually find an ε-robust solution. – Then, update the boundaries according to the answer.

A Bound for Problem Robustness • Problem robustness is only bounded by the truthfulness constraints. – Again, shifting and rescaling takes care of the other constraints. • A simple bound can be derived: ω2 px εx ε x’ px’

Mechanisms for Multiple Sellers • Collusion between agents is a critical matter. • If they can move payments and share information, we can treat them as one agent with multiple sources of information. • An exponential number of constraints is needed. • Tension within the group may limit their collusion. • From here on we assume no collusion is possible.

Mechanisms for Multiple Sellers Two main options: 1. Mechanisms that work in only in equilibrium. – Truth telling is profitable only when everyone else does it. – Payments are conditioned on all the information – Other equilibriums may exist. 2. Dominant strategy mechanisms. – It is always better to tell the truth. – Payments are conditioned on the agent’s own information only (And the verifier).

A Simple Example (2 x 2 x 2( x 1 x 2 Pr(x 1, x 2) Pr(ω=1|x 1, x 2) 0 0 1 1/4 1/4 0 1 - δ 1 δ Pr(ω|x 2=1)=Pr(ω|x 2=0) • Hence no dominant strategy mechanism for player 2 • But a mechanism in equilibrium exists.

A Simple Example (2 x 2 x 2( x 1 x 2 Pr(x 1, x 2) Pr(ω=1|x 1, x 2) 0 0 1 1/4 1/4 0 1 - δ 1 δ • The variable Ω is slightly biased to agree with player 1’s variable. • We can have a dominant strategy mechanism for player 1.

Robust Mechanisms for Many Sellers • Dominant strategy mechanism – Just like the single agent case. May not always exist. • Mechanisms that work in equilibrium- problematic. • An equilibrium is a best response to a best response. • A player must believe that its counterpart will play the equilibrium strategy. • This only happens if it believes that the other believes that it will play the equilibrium. • And so on…

Belief Hierarchies • Assume player A believes the probability is p • player B might conceivably believe it’s p’ • Furthermore it may believe that A believes it is p. ’’ • p’’ may be far from p, and we get further away with every step. P’ P P’’

What can we do? • We can consider bounded players. Only look some distance into the belief hierarchy. • We can create finite belief hierarchies. – The first player has a dominant strategy. – The payment to second player depends only on the first. – Payment to the third only on the previous two – Etc. • Every player considers just beliefs of players that precede him. • They do not care about his beliefs. No loops.

Finite belief hierarchies • Only a single equilibrium. • Very reasonable that it will be played. • Such mechanisms might not always exist • The extreme case: – All agents have a dominant strategy mechanism.

Conclusion • Designing information elicitation mechanisms: – Easy for one agent. – Can be extended easily to robust mechanism – Complicated for many agent. – Robust extension is unclear in equilibrium. – Collusion makes the design even harder.