Robotics Science and Systems MIT 2005 Workshop on

Robotics: Science and Systems, MIT, 2005 Workshop on Modular and Reconfigurable Robots Behavior Synthesis in Self-Organizing Robotic Systems Eric Klavins Assistant Professor Electrical Engineering University of Washington In collaboration with Rob Ghrist (UIUC Mathematics) and Josh Bishop, Sam Burden, JM Mc. New and Nils Napp (UW Students). 55 min

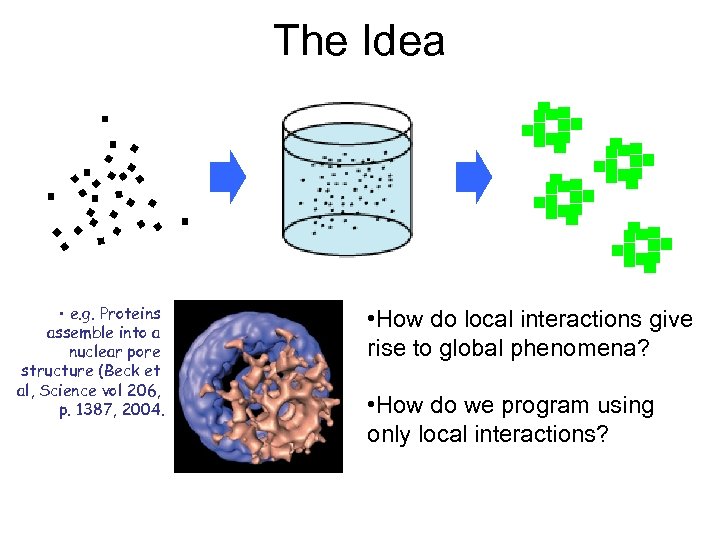
The Idea • e. g. Proteins assemble into a nuclear pore structure (Beck et al, Science vol 206, p. 1387, 2004. • How do local interactions give rise to global phenomena? • How do we program using only local interactions?

Tile Self-Assembly Seems Like a Good Place to Start foam tiles, magnets, air hockey table. active tiles ? e. g. conformational switching passive tiles • Can compute: Wang (1975) • Mesoscale (PDMS, Si, . . . ): Whitesides, (1999 etc. ) and others • Can make from DNA: Winfree (1998) Electrical connections Parviz et al.

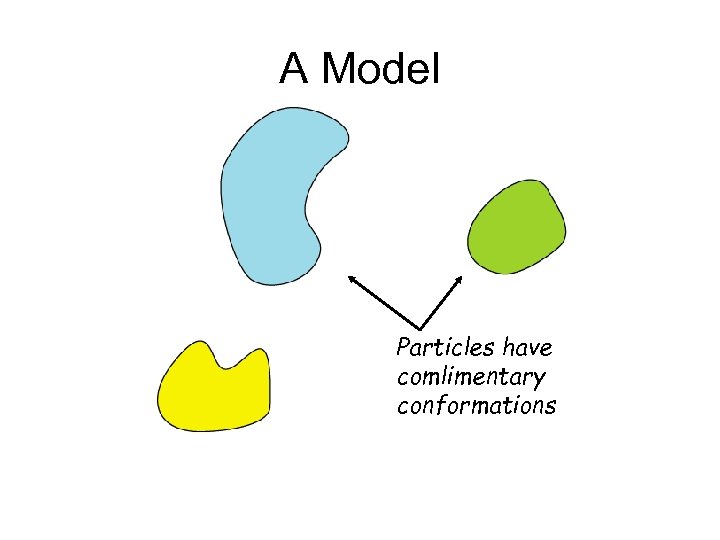
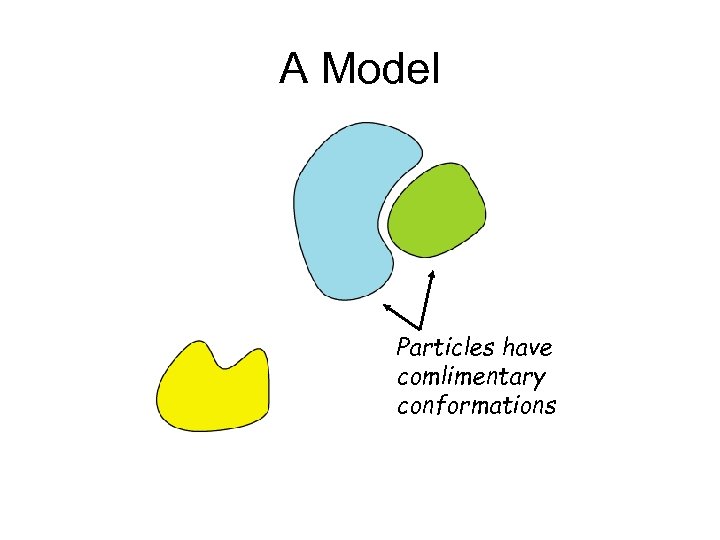
A Model Particles have comlimentary conformations

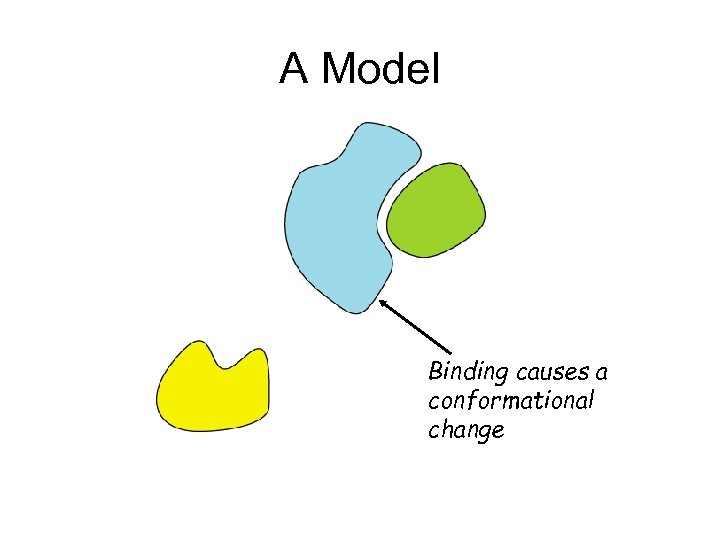
A Model Binding causes a conformational change

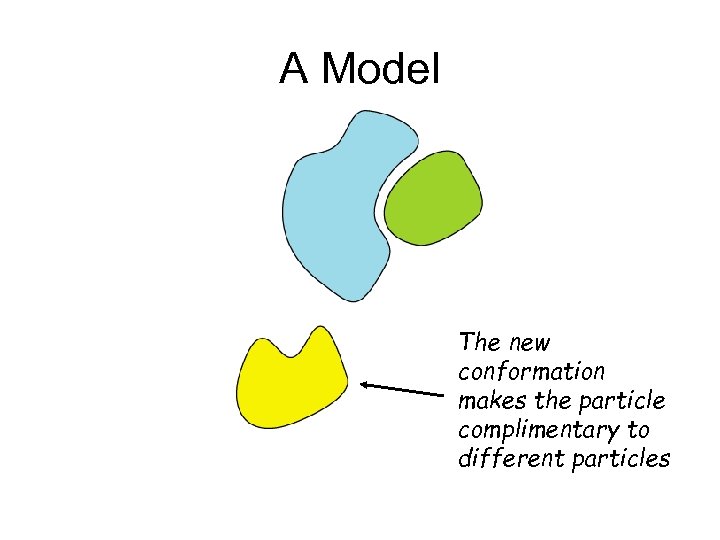
A Model The new conformation makes the particle complimentary to different particles

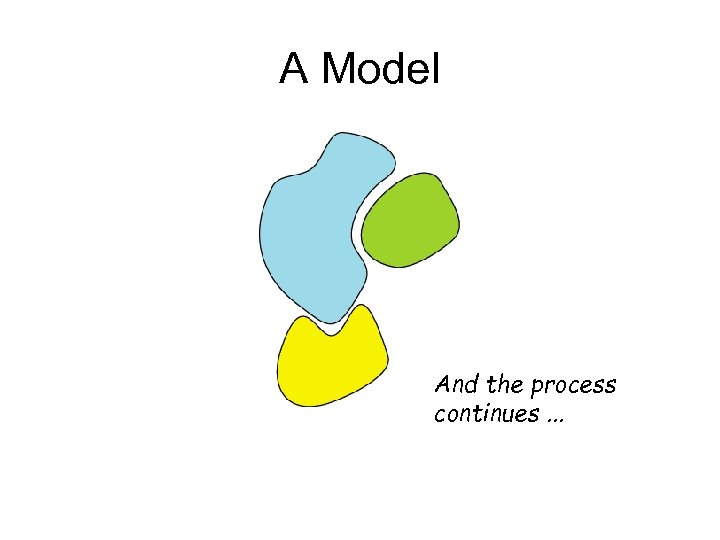
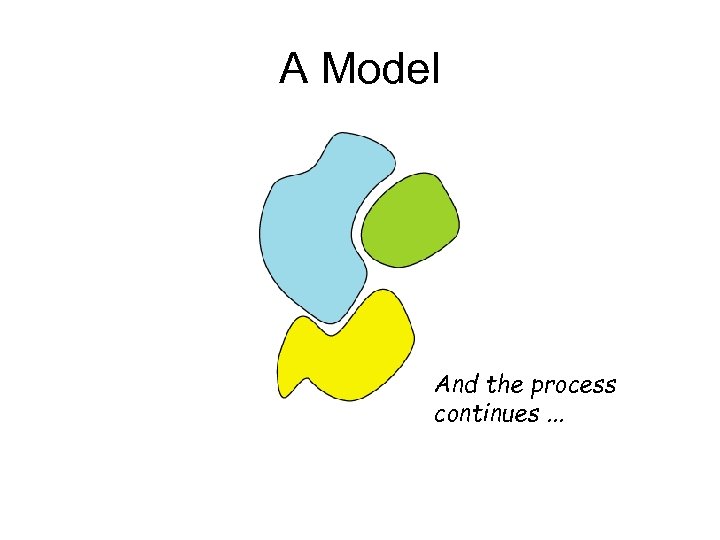
A Model And the process continues. . .

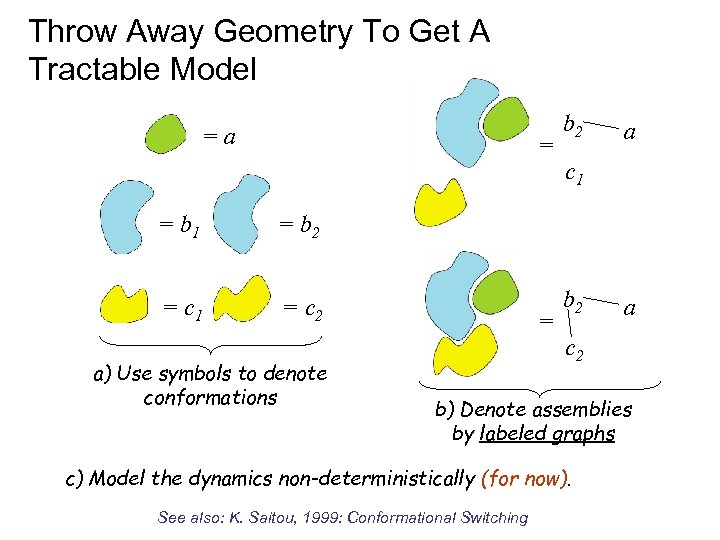
Throw Away Geometry To Get A Tractable Model =a = = b 1 = c 2 a c 1 = b 2 = c 1 b 2 a) Use symbols to denote conformations = b 2 a c 2 b) Denote assemblies by labeled graphs c) Model the dynamics non-deterministically (for now). See also: K. Saitou, 1999: Conformational Switching

Graph Grammars Klavins, Ghrist and Lipsky, IEEE TAC (To Appear) See Also, Courcelle: Handbook of TCS, Vol B A system is modeled by a simple labeled graph: parts connections c a a a b a c states b d b a a b

Graph Grammars Klavins, Ghrist and Lipsky, IEEE TAC (To Appear) See Also, Courcelle: Handbook of TCS, Vol B An rule and a monomorphism lead to a new graph. c a a b d a e f g b a c d b a a b

Graph Grammars Klavins, Ghrist and Lipsky, IEEE TAC (To Appear) See Also, Courcelle: Handbook of TCS, Vol B An rule and a monomorphism lead to a new graph. c a a b d a e f g b a e a c f b a g b • Small rules model local interactions. • Commutative rules model parallelism via interleaving.

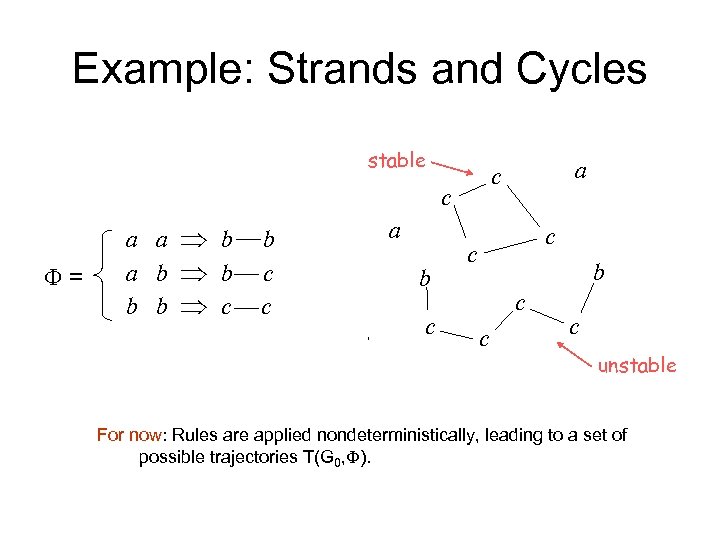
Example: Strands and Cycles stable c a b = a a b a b b b b c b c c a b c a a c b a c a b c b a unstable For now: Rules are applied nondeterministically, leading to a set of possible trajectories T(G 0, ).

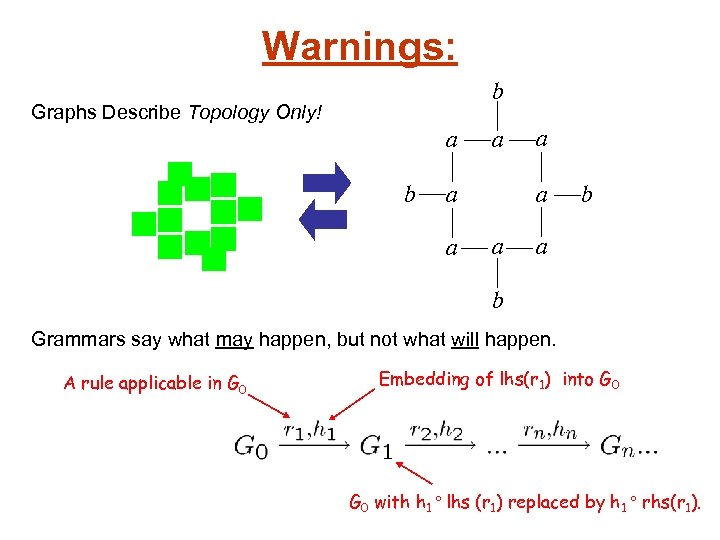
Warnings: b Graphs Describe Topology Only! a b a a a b a b Grammars say what may happen, but not what will happen. A rule applicable in G 0 Embedding of lhs(r 1) into G 0 with h 1 lhs (r 1) replaced by h 1 rhs(r 1).

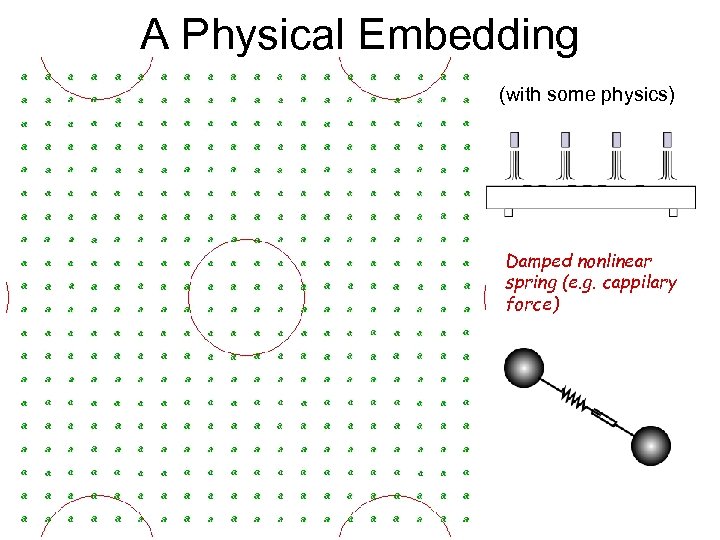
A Physical Embedding (with some physics) Damped nonlinear spring (e. g. cappilary force)

Example II: Self-Replication Klavins, ICMENS 2004 Attach raw materials Move right Close loops Move Left Break strands

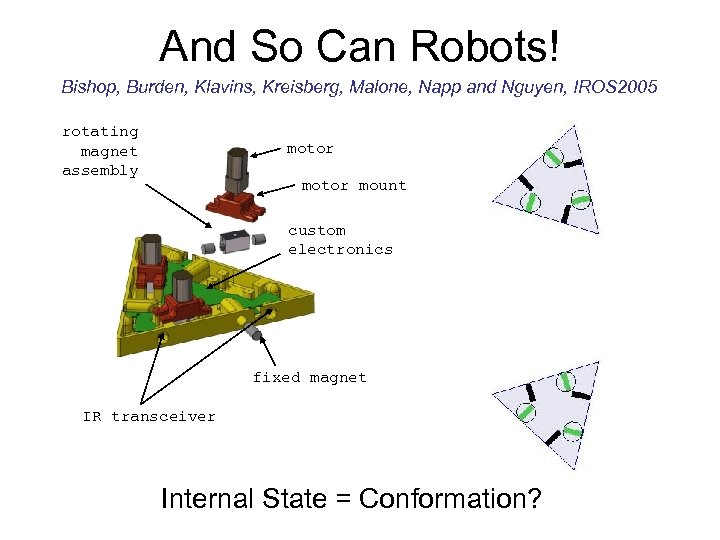
And So Can Robots! Bishop, Burden, Klavins, Kreisberg, Malone, Napp and Nguyen, IROS 2005 rotating magnet assembly motor mount custom electronics fixed magnet IR transceiver Internal State = Conformation?

Version 1. 0 Bishop, Burden, Klavins, Kreisberg, Malone, Napp and Nguyen, IROS 2005 Initial test of latching mechanism 1 cm Compare: Modular and Reconfigurable robots (e. g. Yim, Chirickjian, Murata, Rus, Lipson and many others).

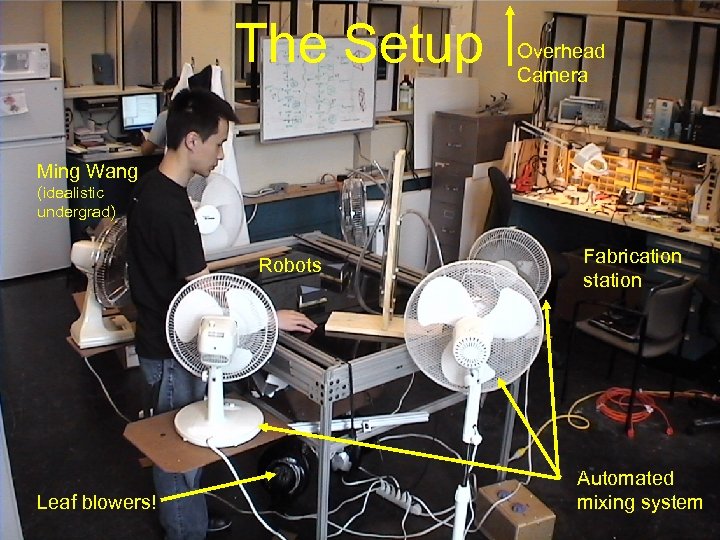
The Setup Overhead Camera Ming Wang (idealistic undergrad) Robots Leaf blowers! Fabrication station Automated mixing system

A Test of the Latching Mechanism Four parts interacting on an air table (from 30 fps vision tracking system) So how do you program them?

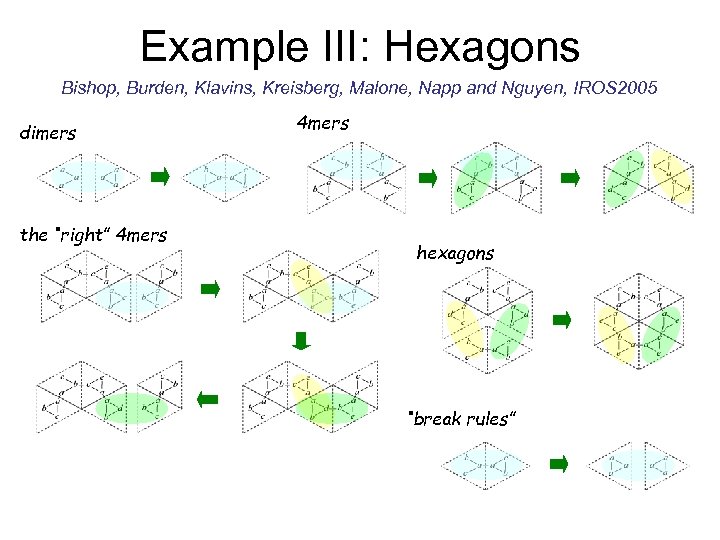
Example III: Hexagons Bishop, Burden, Klavins, Kreisberg, Malone, Napp and Nguyen, IROS 2005 dimers the “right” 4 mers hexagons “break rules”

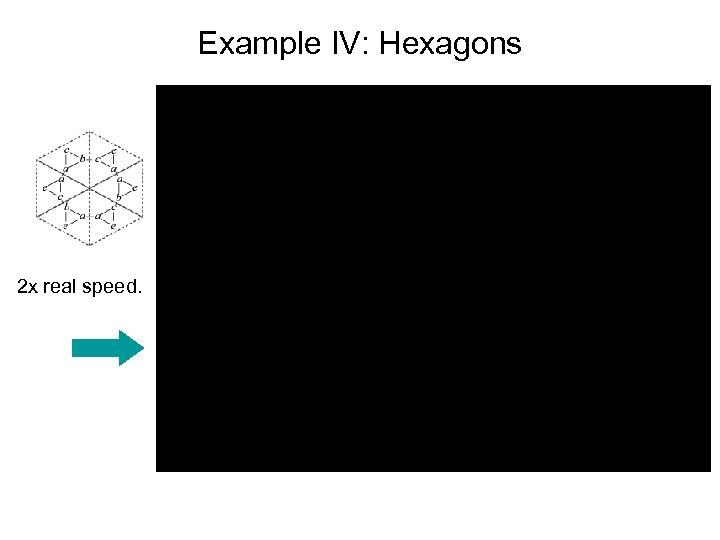
Example IV: Hexagons 2 x real speed.

Local Minima • To avoid deadlock, add rules of the form (V, E, l) (V, , x. a) that are executed randomly (Klavins, ICRA 2002) • Note: Statistical mechanics takes care of this, but the above rules make for bigger energy differences (Compare: DNA Free Energy Landscapes)

More Examples . . .

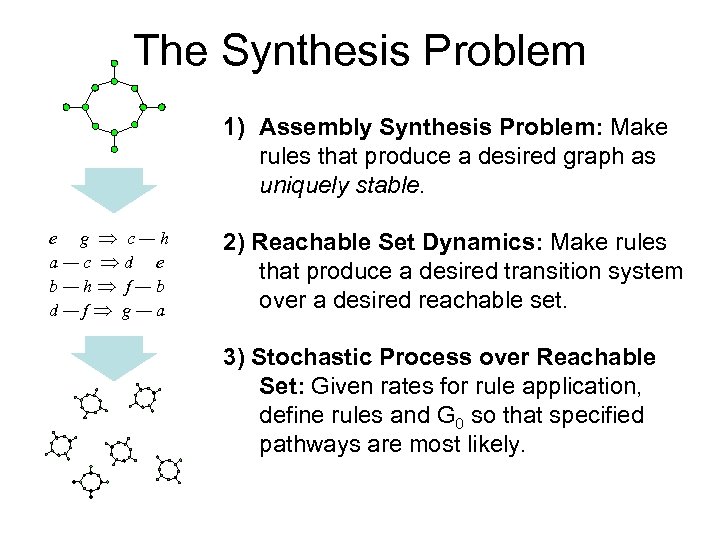
The Synthesis Problem 1) Assembly Synthesis Problem: Make rules that produce a desired graph as uniquely stable. e g c—h a—c d e b—h f—b d—f g—a 2) Reachable Set Dynamics: Make rules that produce a desired transition system over a desired reachable set. 3) Stochastic Process over Reachable Set: Given rates for rule application, define rules and G 0 so that specified pathways are most likely.

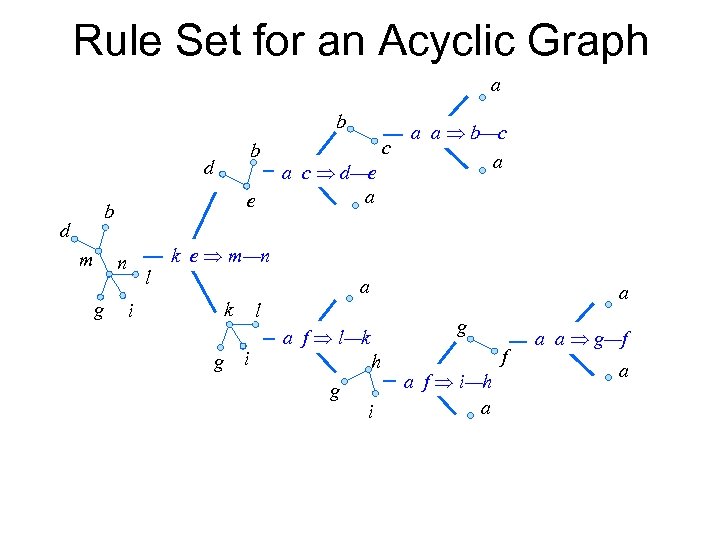
Rule Set for an Acyclic Graph a b b d e b d m n g l i a c d—e a a a b—c c a k e m—n a k g i a l g a f l—k h g i f a f i—h a a a g—f a

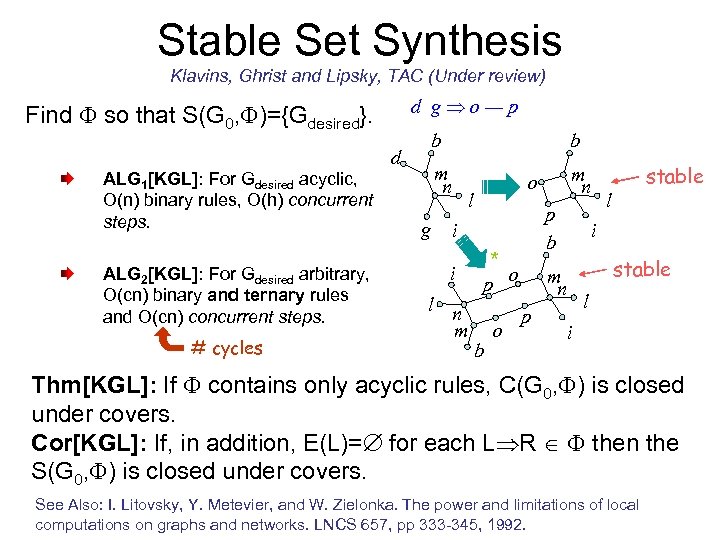
Stable Set Synthesis Klavins, Ghrist and Lipsky, TAC (Under review) d g o—p Find so that S(G 0, )={Gdesired}. d ALG 1[KGL]: For Gdesired acyclic, O(n) binary rules, O(h) concurrent steps. ALG 2[KGL]: For Gdesired arbitrary, O(cn) binary and ternary rules and O(cn) concurrent steps. # cycles b b m n g l p b i i l n m m n o * o p b o l i m n p stable l i Thm[KGL]: If contains only acyclic rules, C(G 0, ) is closed under covers. Cor[KGL]: If, in addition, E(L)= for each L R then the S(G 0, ) is closed under covers. See Also: I. Litovsky, Y. Metevier, and W. Zielonka. The power and limitations of local computations on graphs and networks. LNCS 657, pp 333 -345, 1992.

The Covering Problem (Proof Sketch)

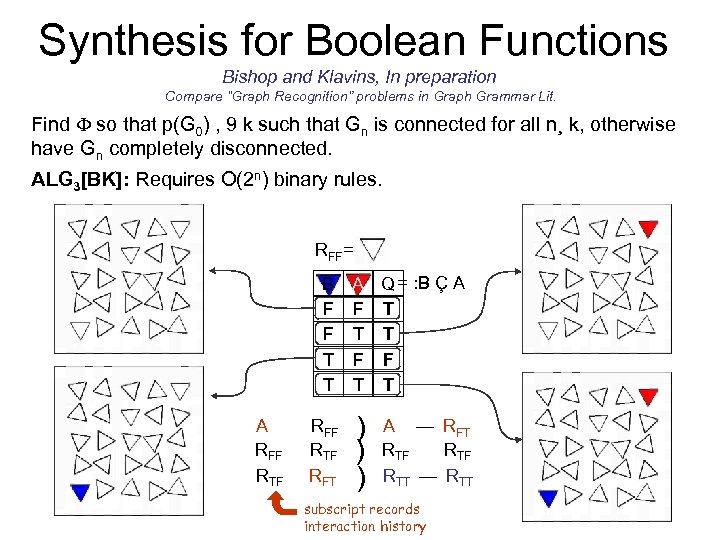
Synthesis for Boolean Functions Bishop and Klavins, In preparation Compare “Graph Recognition” problems in Graph Grammar Lit. Find so that p(G 0) , 9 k such that Gn is connected for all n¸ k, otherwise have Gn completely disconnected. ALG 3[BK]: Requires O(2 n) binary rules. RFF= B F F T T A RFF RTF RFT A Q = : B Ç A F T T T F F T T ) ) ) A — RFT RTF RTT — RTT subscript records interaction history

Specify Behaviors From the Point of View of the Particles Idea: Consider the transition system induced by a graph grammar modulo neighborhood equivalence. Graphs are U 0 and U 1 equivalent, but not U 2 equivalent.

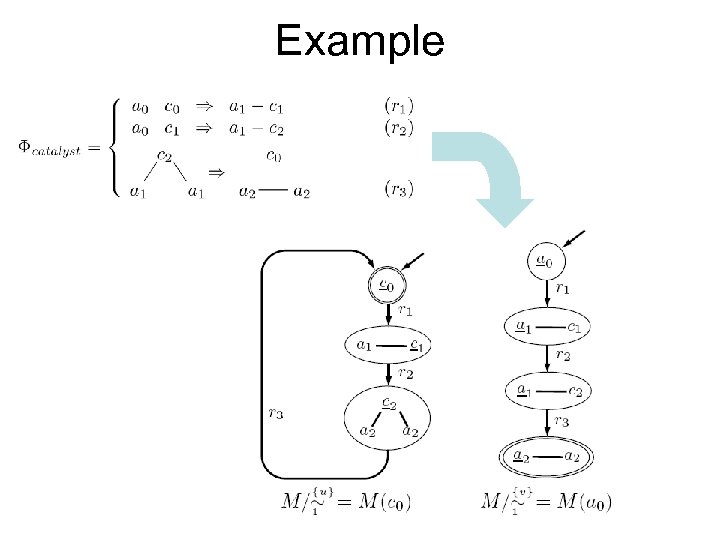
Example

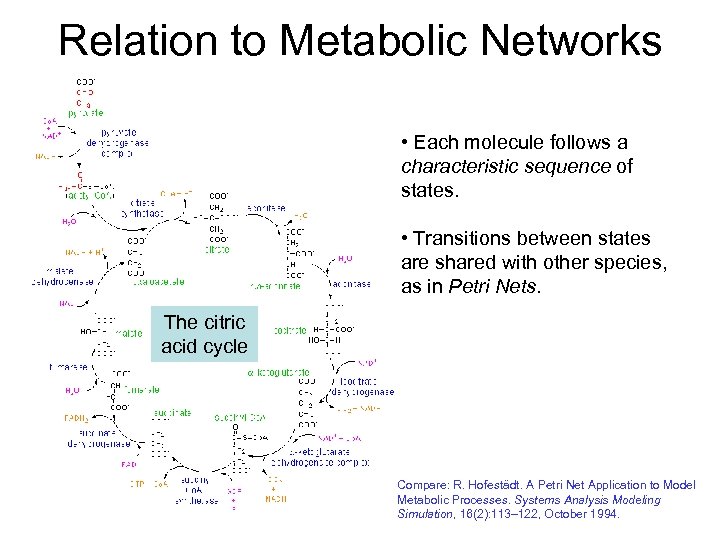
Relation to Metabolic Networks • Each molecule follows a characteristic sequence of states. • Transitions between states are shared with other species, as in Petri Nets. The citric acid cycle Compare: R. Hofestädt. A Petri Net Application to Model Metabolic Processes. Systems Analysis Modeling Simulation, 16(2): 113– 122, October 1994.

CAS Generation Problem: Given (G 0, ) find its characteristic automata set. (Dumb) Algorithm 1) Produce trajectories 1, 2, . . . of (G 0, ). 2) Build the neighborhood automaton for each particle for each trajectory. 3) Take equivalence classes modulo neighborhood isomorphism. 4) Compare: Metabolic network identification.

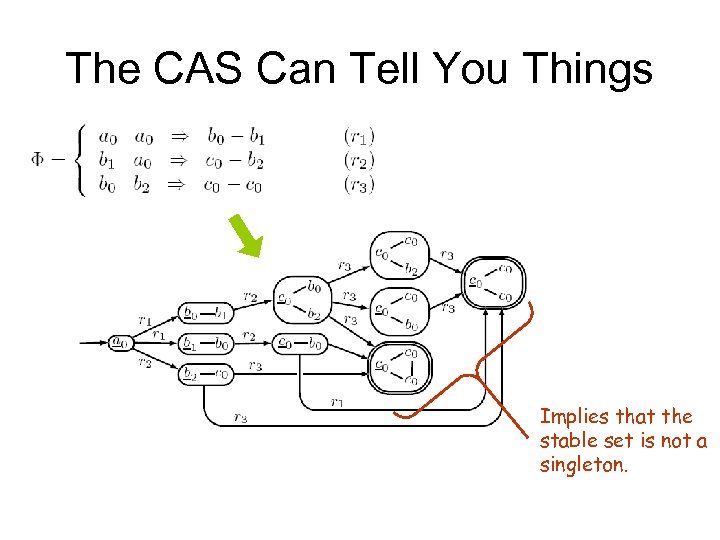
The CAS Can Tell You Things Implies that the stable set is not a singleton.

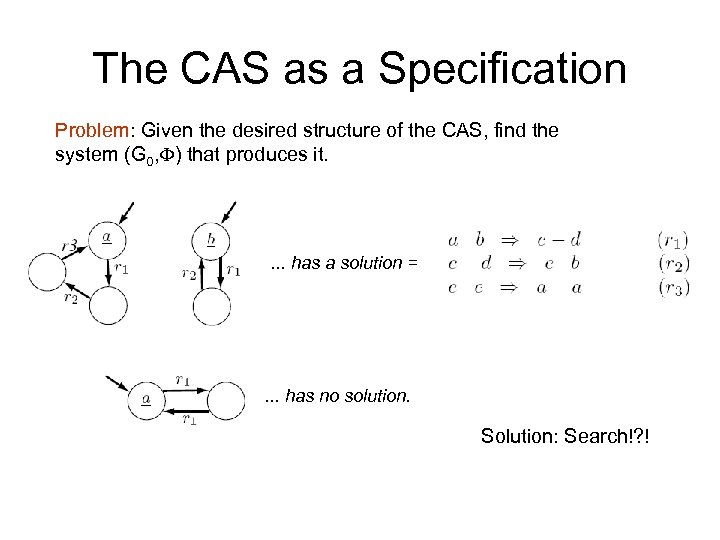
The CAS as a Specification Problem: Given the desired structure of the CAS, find the system (G 0, ) that produces it. . has a solution = . . . has no solution. Solution: Search!? !

Rates Issue 1: Our systems are usually stochastic. Issue 2: The number of states is (usually) exponential in the number of particles. Rate from G to G’ Rate out of G

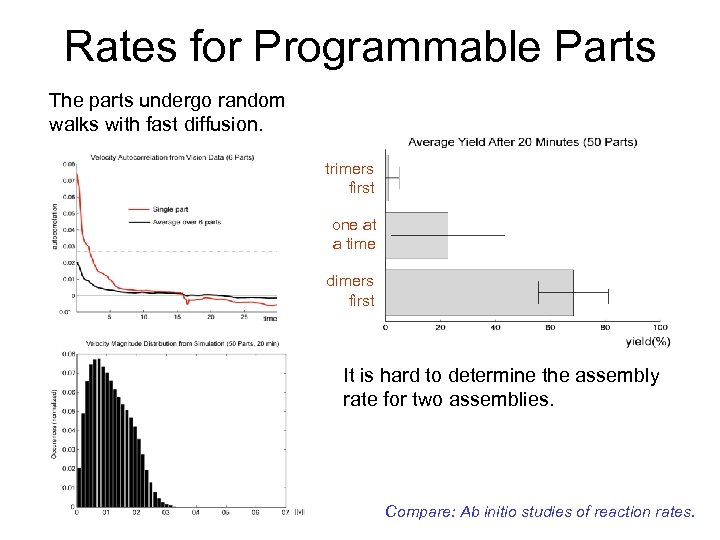
Rates for Programmable Parts The parts undergo random walks with fast diffusion. trimers first one at a time dimers first It is hard to determine the assembly rate for two assemblies. Compare: Ab initio studies of reaction rates.

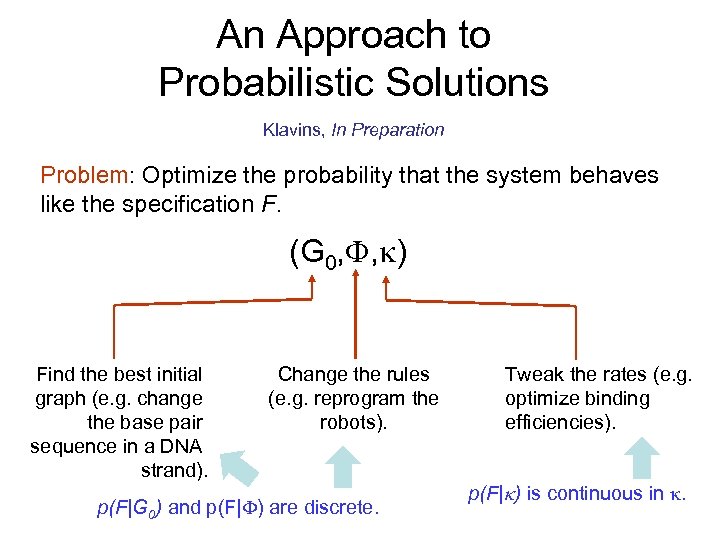
An Approach to Probabilistic Solutions Klavins, In Preparation Problem: Optimize the probability that the system behaves like the specification F. (G 0, , ) Find the best initial graph (e. g. change the base pair sequence in a DNA strand). Change the rules (e. g. reprogram the robots). p(F|G 0) and p(F| ) are discrete. Tweak the rates (e. g. optimize binding efficiencies). p(F| ) is continuous in .

Optimizing Example: Find k so that (k) behaves like the specification F half of the time. F: (k) Approach: 1) Sample behaviors of (k) to estimate |p(F| (k))-0. 5| for a given k. 2) Use these samples to estimate the gradient and do gradient descent. J. Spall, Ch. 14: Simulation-Based Optimization, Introduction to Stochastic Search and Optimization: Estimate, Simulation and Control, Wiley & Sons, 2003.

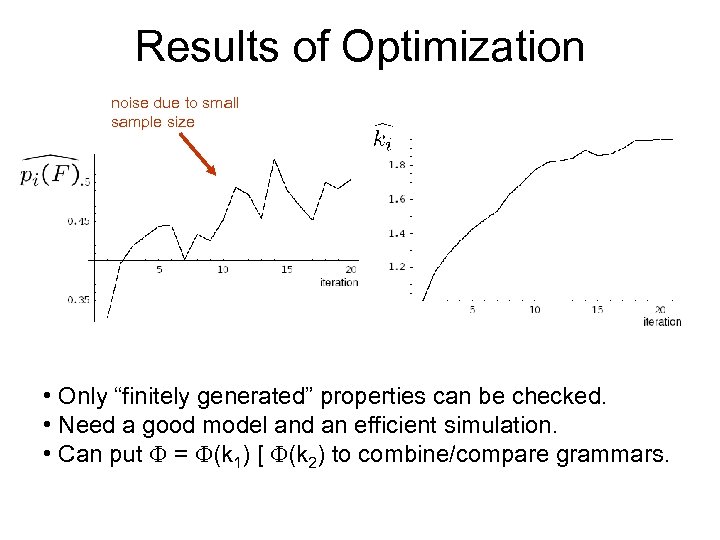
Results of Optimization noise due to small sample size • Only “finitely generated” properties can be checked. • Need a good model and an efficient simulation. • Can put = (k 1) [ (k 2) to combine/compare grammars.

Acknowledgements CAREER: Programmed Robotic Self-Assembly COLLABORATORS Karl Böhringer Robert Ghrist STUDENTS Josh Bishop Sam Burden Richard Kreisberg William Malone Nils Napp Tho Nguyen Fayette Shaw Ming Wang

Ongoing Work Modeling Synthesis Complexity Statistical Dynamics Robots Swarming MEMs DNA