Robotics Chapter 5 Path and Trajectory Planning

Robotics Chapter 5 – Path and Trajectory Planning Dr. Amit Goradia

Topics • • • Introduction – Coordinate transformations – Forward Kinematics Inverse Kinematics Velocity Kinematics Trajectory Planning Robot Dynamics (Introduction) Force Control (Introduction) Task Planning - 2 hrs 6 hrs 2 hrs 1 hrs 6 hrs

Robot Motion Planning • Path planning – Geometric path – Issues: obstacle avoidance, shortest path • Trajectory planning, – “interpolate” or “approximate” the desired path by a class of polynomial functions – Generate a sequence of time-based “control set points” for the control of manipulator from the initial configuration to its destination.

Definitions • Configuration: Specification of all the variables that define the system completely – Example: Configuration of a dof robot is • Configuration space (C-space): Set of all configurations • Free configuration: A configuration that does not collide with obstacles • Free space ( F ) : Set of all free configurations – It is a subset of C

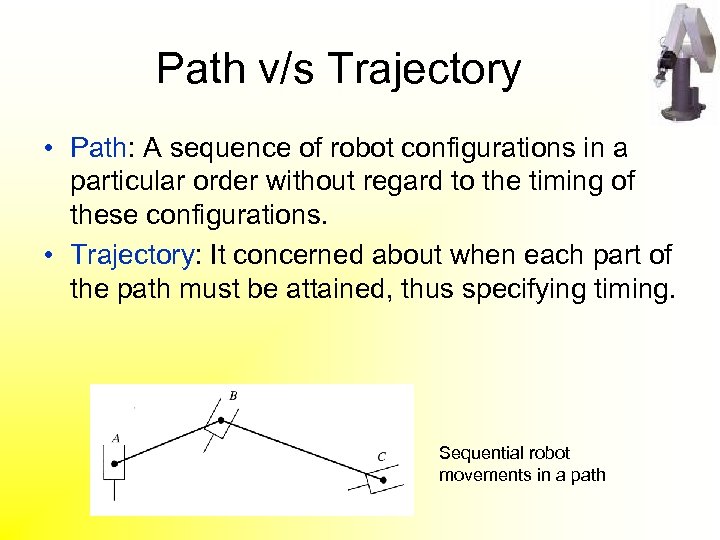
Path v/s Trajectory • Path: A sequence of robot configurations in a particular order without regard to the timing of these configurations. • Trajectory: It concerned about when each part of the path must be attained, thus specifying timing. Sequential robot movements in a path

Path Planning: Problem Definition • Problem statement: Compute a collision-free path for a rigid or articulated moving object among static obstacles. • Input – Geometry of a moving object (a robot, a digital actor, or a molecule) and obstacles – How does the robot move? – Kinematics of the robot (degrees of freedom) – Initial and goal robot configurations (positions & orientations) • Output Continuous sequence of collision-free robot configurations connecting the initial and goal configurations

Trajectory Planning: Problem Definition • Problem statement Turn a specified Cartesianspace trajectory of Pe into appropriate joint position reference values • Input – Cartesian space path – Path constraints including velocity and acceleration limits and singularity analysis. • Output – a series of joint position/velocity reference values to send to the controller

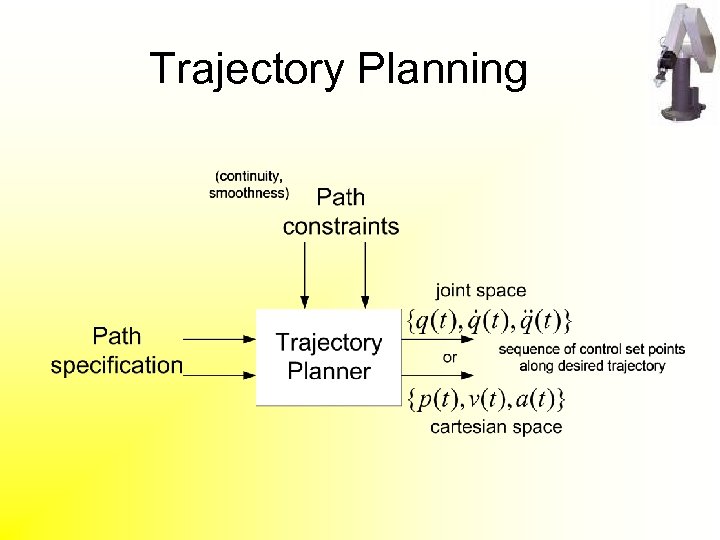
Trajectory Planning

Joint Space v/s Task Space • Joint-space description: – The description of the motion to be made by the robot by its joint values. – The motion between the two points in joint space is not predicted. • Task space description: – The motion between the two points is known at all times and controllable. – It is easy to visualize the trajectory, but is difficult to ensure singularity robustness.

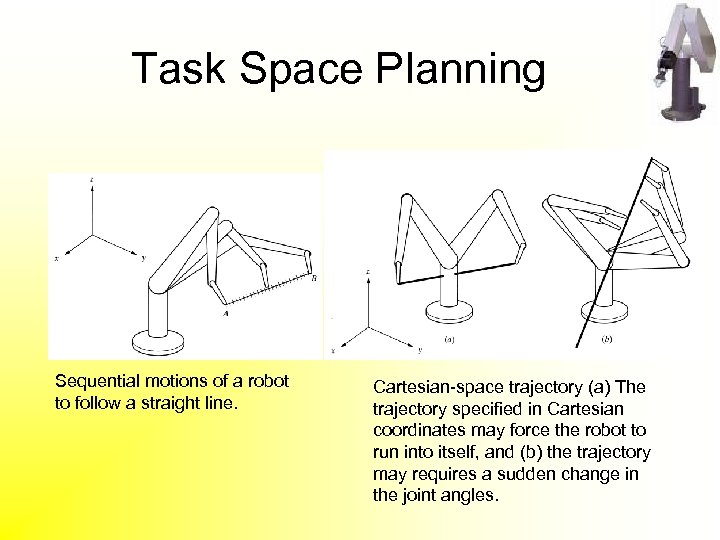
Task Space Planning Sequential motions of a robot to follow a straight line. Cartesian-space trajectory (a) The trajectory specified in Cartesian coordinates may force the robot to run into itself, and (b) the trajectory may requires a sudden change in the joint angles.

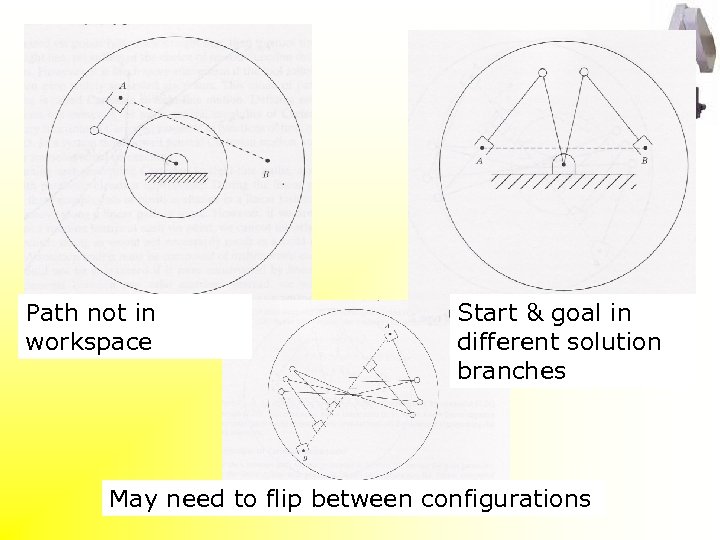
Path not in workspace Start & goal in different solution branches May need to flip between configurations

Trajectory Planning • Point to point motion – Teach initial and final points; intermediate path is not critical and is computed by the controller – Applications: Moving of parts, spot welding, automated loading and unloading of machines; pickand-place motion • Continuous path motion – Used when there is a need to follow a complex path through 3 -D space, possibly at high speeds (spray painting, welding, polishing) – Points generally taught by manual lead through with high speed automatic sampling

Point to Point Motion • Simple point-to-point smooth trajectory with a few constraints on the lift -off and set-down positions. • There are 3 ways a manipulator can move from point to point: – slew motion – joint interpolated motion – straight line motion • Slew motion: all joints move to their required new position as quickly as possible. All axes begin motion at the same time but arrive at their destination at different times. This generally results in joint wear and unpredictable arm motions. • Joint interpolated motion requires the controller to calculate which joint will take the longest to arrive at its destination and slow other joints down accordingly. A separate velocity is calculated for each axis. Manipulator motion is generally smooth and wear is reduced. • Straight line motion is a particular case of continuous path motion.

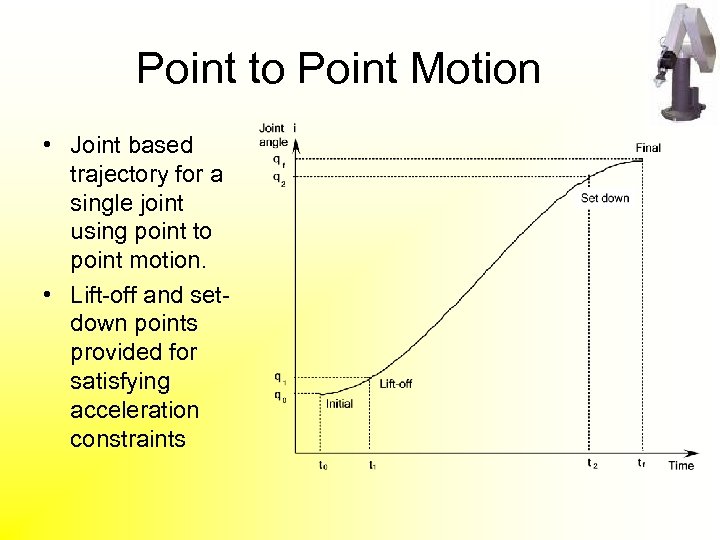
Point to Point Motion • Joint based trajectory for a single joint using point to point motion. • Lift-off and setdown points provided for satisfying acceleration constraints

Cubic Polynomial Trajectories • Single joint (1 DOF): – – We Know , We also Know Want to find , Where , , and • So we have four Constraints: Lets try a Cubic polynomial

Cubic Polynomial Trajectory • To determine the coefficients we need to look at our boundry conditions. Namely: – – Position at t=0 Velocity at t=0 Position at t=final Velocity at t=final • Plugging these in we get. • Solving for a 2 and a 3

Cubic Polynomial Trajectory • So the an are • If the initial and final velocity is zero then • So finally the acceleration is given by or

Minimum Torque Trajectories • Is a good solution? ? • Solve the following minimization problem: • The solution is:

Quintic Polynomial Trajectory • Cubics allow us to define the position and velocity at each location in the trajectory. However, the acceleration is discontinuous. • If we also want to specify the acceleration we would need a Quintic or order 5 polynomial. • Use the initial and final positions, velocities and accelerations as our boundary conditions to solve for the coefficients.

Quintic Polynomial Trajectory

Quintic Polynomial Trajectory • Compute inverse for each joint

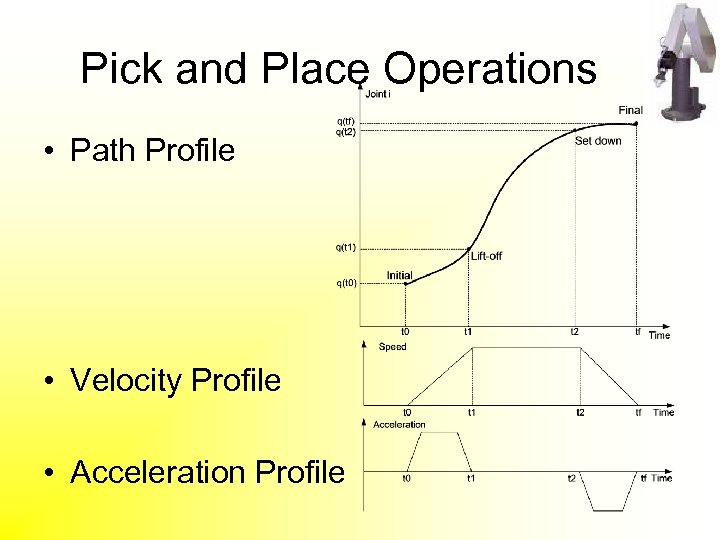
Pick and Place Operations • Path Profile • Velocity Profile • Acceleration Profile

Boundary Conditions 1) 2) 3) 4) 5) Initial position Initial velocity Initial acceleration Lift-off position Continuity in position at t 1 6) Continuity in velocity at t 1 7) Continuity in acceleration at t 1 8) 9) Set-down position Continuity in position at t 2 10) Continuity in velocity at t 2 11) Continuity in acceleration at t 2 12) Final position 13) Final velocity 14) Final acceleration

Known Parameters • Initial and Final – Positions (given) – Velocities (normally 0) – Accelerations (normally 0) • Intermediate Positions (Lift-off and setdown) – Positions (given) – Velocities (continuous with previous trajectory segment) – Accelerations (continuous with previous trajectory segment)

Solution • Nth order polynomial must satisfy N+1 conditions • 13 th order polynomial • 4 -3 -4 trajectory t 0 t 1, 5 unknowns t 1 t 2, 4 unknowns t 2 tf, 5 unknowns

Task Space Trajectory Planning • Procedure: – Obtain function for task space path – Sample function to get discrete points (in task space) – Apply IK and Jacobian calculations – Fit functions to joints – Sample to get discrete reference points (in joint space).

Sample Task Space Analytic Functions • Analytic function to describe task space motion: • Differentiate to get rate of change • Sample trajectory to get m sample points

Inverse Kinematics and Jacobian • Use Inverse Kinematics to convert task space trajectory into joint space vector. – Handle multiple solutions – Handle problems related to existence of solutions m ~ 10

Inverse Kinematics and Jacobian • Using Inverse Jacobian convert task space velocities to joint space velocities – Handle singular configurations

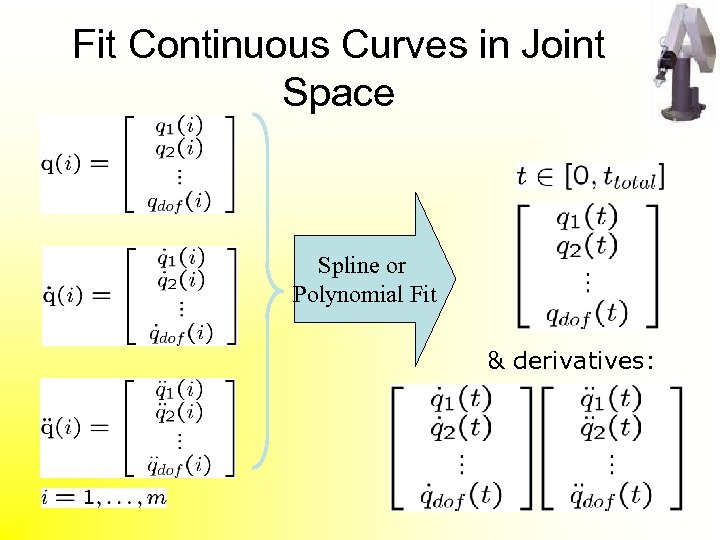
Fit Continuous Curves in Joint Space Spline or Polynomial Fit & derivatives:

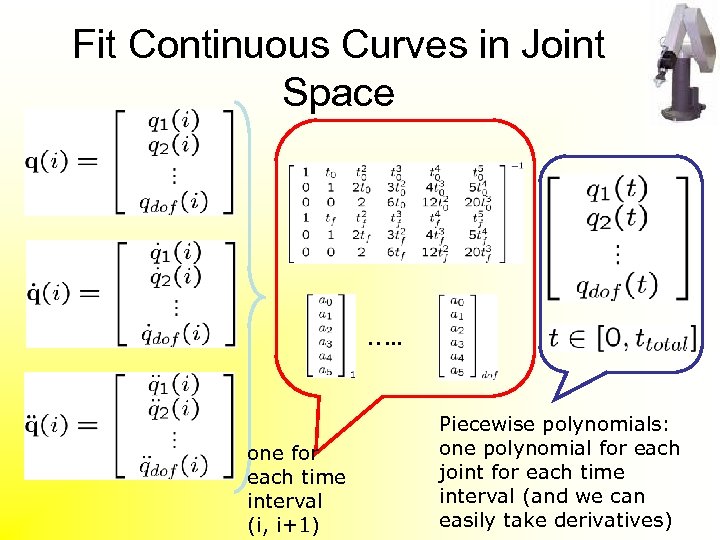
Fit Continuous Curves in Joint Space …. . one for each time interval (i, i+1) Piecewise polynomials: one polynomial for each joint for each time interval (and we can easily take derivatives)

Sample Continuous Curves in Joint Space • Sample Joint positions and speeds Sample N ~ 1000+

Example Straight Line Motion • Parameterize a straight line using time – x(t), y(t), f(t) • Move along line with constant velocity v • Equation of line: • Velocity: • Solve

Parameterize the Straight Line • Velocity:

Sample Continuous Path

Path Planning Approaches: Classifications 1. Methods exploring a “search graph” – – Attempt to capture the topology of the C-space Pre-processing of the C-space independently of any goal Multiple query type Examples: PRM’s, Voronoi diagrams, Cellular decomposition 2. Methods incrementally building a search tree – – No attempt at capturing the topology of the C-space Goal dependent methods Single query type Examples: A* algorithm, Rapidly-exploring Random Trees(RRT)

Potential Field Approaches • A heuristic function (artificial potential field) is defined on the configuration space to steer robot towards a goal through gradient descent. • Random walks are used to escape local minimum traps. • Efficient for holonomic planning but depends on the choice of a good heuristic function. • Choosing a good heuristic function is difficult when obstacles and differential constraints are added to the problem.

Path Planning Approaches • Probabilistic Roadmaps – A graph is constructed on configuration space by generating random configurations and attempting to connect pairs of nearby configurations with a local planner. – Local planning is efficient – Connecting configurations is a difficult task, particularly for complicated nonholonomic dynamical systems. (nonlinear control problem)