РОБАСТНОЕ СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ Грубые ошибки и методы их

РОБАСТНОЕ СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ Грубые ошибки и методы их выявления в статистической совокупности данных n

n При исследовании статистических совокупностей часто приходится иметь дело с данными, отклоняющимися от основного массива, т. е. с ошибками, или выбросами.

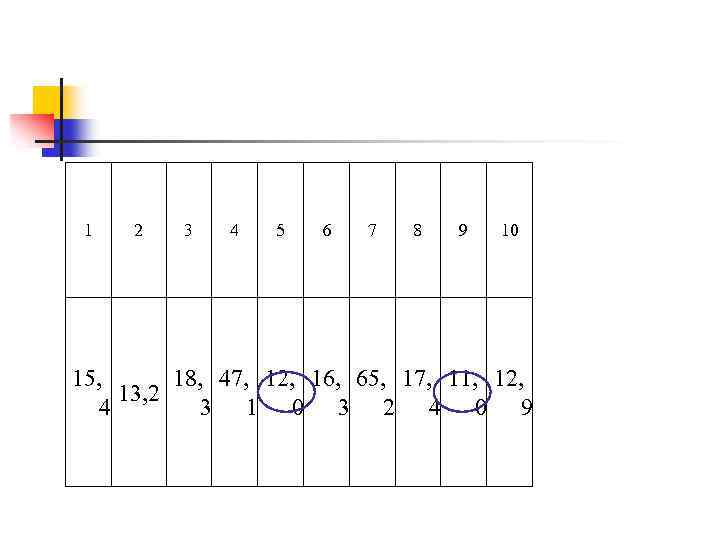
1 2 3 4 5 6 7 8 9 10 15, 18, 47, 12, 16, 65, 17, 11, 12, 13, 2 4 3 1 0 3 2 4 0 9

n При выявлении подобных «выбросов» возникают серьезные вопросы: являются ли отклоняющиеся данные действительно ошибками (например, регистрации) или это реальные значения и как получить адекватные оценки для параметров изучаемой совокупности. Решением подобных вопросов занимается специальный раздел статистики — робастное (устойчивое) оценивание.

n Методы робастного оценивания — это статистические методы, которые позволяют получать достаточно надежные оценки статистической совокупности с учетом неявности закона ее распределения и наличия существенных отклонений в значениях данных. У истоков развития методов робастного оценивания стояли американский статистик Д. Тьюки и швейцарский математик П. Хубер.

При решении задач робастного оценивания выделяют два типа данных, засоряющих статистическую совокупность. n данные, несущественно отличающиеся от значений, которые наиболее часто встречаются в изучаемой совокупности. n резко выделяющиеся на фоне изучаемой совокупности, их называют «засорением» или «грубыми ошибками» , они оказывают сильное искажающее воздействие на аналитические результаты.

основные причины появления грубых ошибок: • Специфические особенности отдельных элементов изучаемой совокупности. Как правило, они приводят к появлению случайных, или «нормальных» ( «обычных» ) отклонений. • Неправильное причисление элементов к исследуемой совокупности, например, ошибки группировки, ошибки при организации наблюдения и т. п. • Грубые ошибки при регистрации и обработке данных.

При обработке «грубых» ошибок (засорений) выделяют два основных подхода. n устранение из выборочной совокупности ошибок и оценку параметров по оставшимся «истинным» значениям n Усеченная выборка

Второй подход предполагает в каждом случае с грубой ошибкой выделение истинных значений признака и собственно ошибки n х=хист+ξ осуществляется модификация данных таким образом, чтобы искажающий элемент ξ получил нормальное распределение с нулевым математическим ожиданием

Алгоритм обработки «засорений» включает последовательное выполнение шагов: 1) распознавание ошибок в данных; 2) выбор метода и проведение робастного оценивания данных; 3) критериальная или логическая проверка и интерпретация результатов устойчивого оценивания.

Простой формальный прием для обнаружения грубых ошибок основывается на расчете Ткритерия Граббса: n n где х — выборочная средняя. Ее оценка предпочтительна по истинным данным σ — выборочное среднеквадратическое отклонение случайной величины.

Наблюденные значения Т-критерия сравнивают с пороговыми, заданными соответствующим распределением. n Проверяемые признаковые значения относят к классу выбросов, если Тн >Ткр (Ткр=Тα, h). Если Тн<Ткр, то считается, что эти значения несущественно отличаются от других данных, и не будут давать сильного искажающего эффекта.

n Критерий Граббса прост и легко применим в анализе, но имеет существенные недостатки. В частности, исследователи обращают внимание на его недостаточную точность (часто дает весьма грубые оценки) и, кроме того, он «нечувствителен» к маскирующим эффектам, когда выбросы группируются достаточно близко друг от друга в отдаленности от основной массы наблюдений.

n Более точными по сравнению со статистикой Граббса оценками грубых ошибок признаются L- и Е-критерии, предложенные американскими статистиками Г. Титьеном и Г. Муром:

L-критерий исчисляется для выявления грубых ошибок в верхней части ранжированного ряда данных: число наблюдений с резко отклоняющимися значениями признака объем выборки средняя, которую рассчитывают по п - k наблюдениям, остающимися после отбрасывания k грубых ошибок «сверху» ранжированного ряда данных

L'-критерий применяется для выявления грубых ошибок в данных, расположенных в нижней части ранжированного ряда данных

E-критерий используется, когда в выборке имеются предположительно грубые ошибки с наибольшими и наименьшими значениями, т. е. расположенные в верхней и нижней частях ранжированного ряда данных

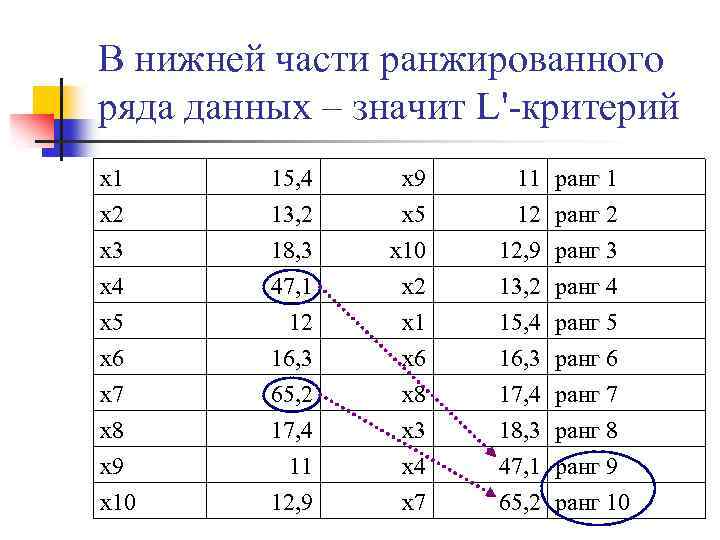
В нижней части ранжированного ряда данных – значит L'-критерий х1 х2 х3 х4 15, 4 13, 2 18, 3 47, 1 х9 х5 х10 х2 11 12 12, 9 13, 2 ранг 1 ранг 2 ранг 3 ранг 4 х5 х6 х7 х8 х9 х10 12 16, 3 65, 2 17, 4 11 12, 9 х1 х6 х8 х3 х4 х7 15, 4 16, 3 17, 4 18, 3 47, 1 65, 2 ранг 5 ранг 6 ранг 7 ранг 8 ранг 9 ранг 10

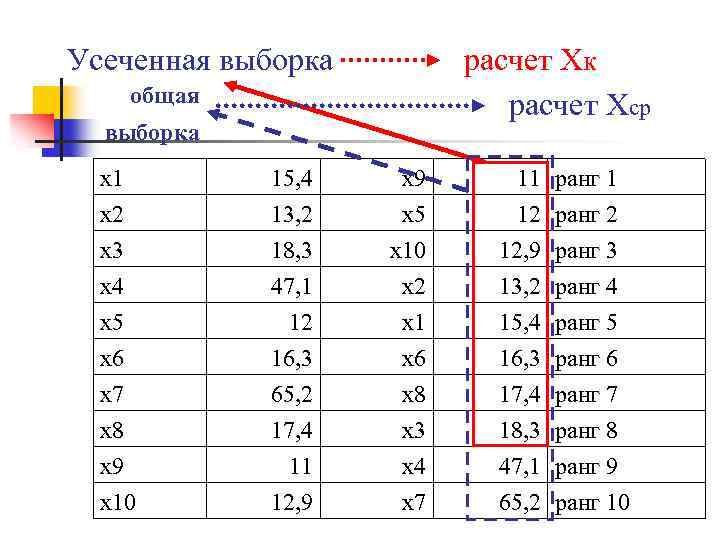
Усеченная выборка расчет Хк расчет Хср общая выборка х1 х2 х3 х4 15, 4 13, 2 18, 3 47, 1 х9 х5 х10 х2 11 12 12, 9 13, 2 ранг 1 ранг 2 ранг 3 ранг 4 х5 х6 х7 х8 х9 х10 12 16, 3 65, 2 17, 4 11 12, 9 х1 х6 х8 х3 х4 х7 15, 4 16, 3 17, 4 18, 3 47, 1 65, 2 ранг 5 ранг 6 ранг 7 ранг 8 ранг 9 ранг 10

n Все три критерия L, L' и Е имеют табулированные критические значения для заданного уровня значимости α при известном объеме выборки п и предполагаемом числе ошибок k. Если наблюденные значения критериев оказываются меньше пороговых Са, k, то ошибки в данных, подвергаемые проверке, признаются грубыми, существенно отклоняющимися от основного массива данных. При L, L', Е> Са, k данные гипотетически предполагаются типичными для изучаемой выборочной совокупности.

Графический метод

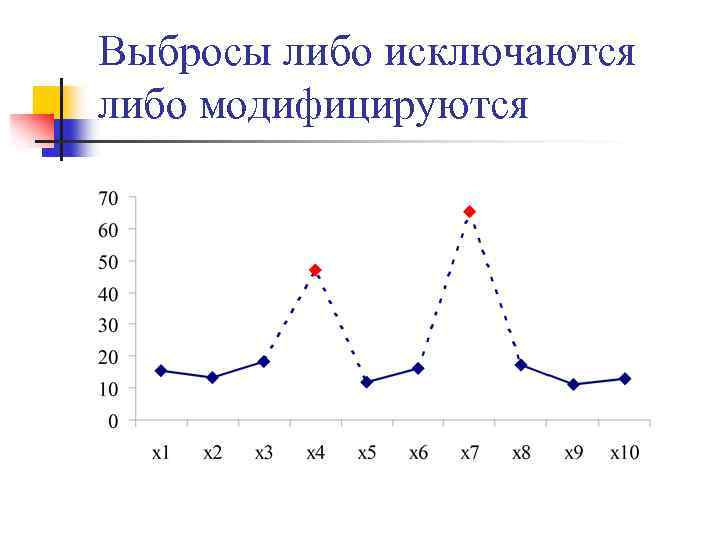
Выбросы либо исключаются либо модифицируются

Методы исчисления устойчивых статистических оценок: Пуанкаре, Винзора, Хубера n После обнаружения выбросов в данных решается задача оценивания параметров выборочной совокупности. При этом, как выше уже сказано, используются два основных подхода: экстремальные значения (грубые ошибки) отбрасываются либо модифицируются.

Американский статистик Пуанкаре n предложил следующую формулу для расчета средней по усеченной совокупности (урезанную среднюю): объем выборочной совокупности число грубых ошибок k≤ a∙n — целая часть от произведения a∙n, где п – объем выборочной совокупности, а α – некоторая функция величины засорения выборки ξ. Значения α находят по специальным таблицам. Обычно α колеблется в пределах от нуля до 0, 5.

Другой подход демонстрирует оценка Винзора она предполагает замену признаковых значений, засоряющих выборку, на модифицированные (винзорированные) значения с устраненными или уменьшенными ошибками. Средняя по Винзору определяется также с известным заранее уровнем а (0< α < 1/2) по формуле:

n n По аналогии с оценками Т(α) и W(α), т. е. соответственно по усеченной совокупности, или винзорированным данным, могут быть найдены не только средние величины, но и другие оценки параметров статистической совокупности, например, вариации, моды, медианы и т. п. Приемы робастного оценивания Пуанкаре и Винзора дают хорошие результаты на выборках с симметричным распределением засорений, когда грубые ошибки группируются примерно на одном расстоянии от центра в нижней и верхней частях статистической совокупности.

n Наряду с уже названными методами робастного оценивания, широкое распространение имеет ставший классическим подход Хубера. Он напоминает процедуры для последовательного «улучшения» данных по Винзору. При этом используется некоторая исходная величина k, определяемая с учетом степени «засорения» статистической совокупности ξ; и определяющая шаг модификации резко отличающихся наблюдений (см. табл. 5. 6).

Оценка средней величины по методу Хубера производится по формуле: где – – численность группы наблюдений из совокупности, n 1 устойчивая оценка, определяется при помощи итеративных процедур; отличающихся наименьшими значениями: xi < Θ - k, или k - величина, которая допускается в качестве отклонения от значения в интервале (-∞; Θ - k); центра совокупности, принимает постоянные значения с учетом п 2 – численность группы наблюдений из совокупности, удельного веса грубых ошибок в совокупности данных ξ отличающихся наибольшими значениями: xi < Θ + k, или значения в интервале (Θ + k; ∞).

ВЫВОДЫ: При обнаружении «засорения» , или «грубых ошибок» , в совокупности данных, т. е. значений, резко отличающихся от медианных, используются принципы проверки статистических гипотез. Наиболее простыми и распространенными являются методы поиска ошибок Граббса, Титьена и Мура. Если в статистической совокупности действительно выявлены «грубые ошибки» , то для уменьшения их влияния на аналитические результаты рекомендуется применение специальных приемов обработки данных.

ВЫВОДЫ: Сущность этих приемов сводится к одному из двух решений: устранению из совокупности аномальных наблюдений, (усечению совокупности), или модификации резко отличающихся значений с целью уменьшения ошибок в данных. Первое решение представлено в подходе Пуанкаре, второе — в подходах Хубера и Винзора, Само изменение данных, направленное на минимизацию ошибки в них, принято называть как винзорирование.

ВЫВОДЫ: Проверка статистических гипотез и робастное оценивание часто используются как самостоятельные статистические приемы в решении задач оценки качества, оценки адекватности заданным условиям и т. п. n. Представленные методы в комплексе с другими статистическими методами позволяют предварительно анализировать наблюденные значения характерных признаков, выявить в них несоответствия и грубые ошибки, провести модификацию данных, повышающую гомогенность изучаемой совокупности. n