521464e59d816678bcb519cfd18c93fb.ppt
- Количество слайдов: 76

Risk & Return (Portfolio) Basic Terminologies q. Required Return: This comprises of two element; risk-free return and risk premium q. Risk-free return: This is the return required by investors to compensate them for investing in a risk-free investment. 3/17/2018 Compiled by F O Boateng 1

q. Risk-free return serves as compensation to investors for inflation and consumption preference. That is, the fact they are deprived from using their funds whilst tied up in investment. T/Bill rate normally used as surrogate. 3/17/2018 Compiled by F O Boateng 2

q. Risk Premium: This is the risk that the future actual return from a security may vary from the expected return. Thus, if an investor undertakes a risky investment he needs to receive a greater return than the risk-free rate for compensation. 3/17/2018 Compiled by F O Boateng 3

q. For an instance, if an investor holds shares in Q plc. The shares of Q plc are twice as risky as the market with the assumption that, the market returns is 11% and the T/Bill rate is 6%. In this scenario, the required rate of return is calculated as: 3/17/2018 Compiled by F O Boateng 4

• Required Return = Risk-free rate (T/B) + [(market returns – riskfree rate (T/B)] x β • » 6% + (11% - 6%) x 2 • » 6% + 10 • » 16% 3/17/2018 Compiled by F O Boateng 5

• Thus 16% is the return that the investor requires to compensate for the perceived level of risk in A plc, i. e, it the discount rate that needs to be used to appraise an investment in Q plc. 3/17/2018 Compiled by F O Boateng 6

q. Unsystematic/Specific Risk: This refers to the impact on a company’s cash flow of largely random events like industrial relations problems, equipment failure, R&D achievement, changes in senior management team etc. 3/17/2018 Compiled by F O Boateng 7

These random factors tend to cancel out as the number of investments in a portfolio increase. q. Systematic/Market Risk: These are general economic (macroeconomic) factors that affect the cash flows all companies in the stock market in a consistent manner, e. g. , 3/17/2018 Compiled by F O Boateng 8

country’s economic growth rate, corporate tax rate, unemployment level, and interest rates. Since the factors can cause returns to move in the same direction, they cannot cancel out. 3/17/2018 Compiled by F O Boateng 9

• Expected Return: investors receive their returns from shares in the form of dividends and capital gains/losses. The formula for computing annual returns on a share is: • Annual return = D 1 + (P 1 – P 0) P 0 3/17/2018 Compiled by F O Boateng 10

• Where: D 1 = dividend per share P 1 = year – end share price P 0 = share price at the beginning of the year. 3/17/2018 Compiled by F O Boateng 11

• Illustration : Assuming that a dividend of 5 pessewas per share was paid during the year on a share whose value was 100 pessewas ath the beginning of the year and 117 pessewas at the end of the year. The annual returns would be: 3/17/2018 Compiled by F O Boateng 12

5 + (117 – 100) x 100 =22% 100 • The total return is made up of a 5% dividend yield and a 17% capital gain. 3/17/2018 Compiled by F O Boateng 13

THE CONCEPT OF RISK • Risk as defined in finance literature is generally based on the variability of the actual return from the expected return. Statistical measures of variability are the variance and standard deviation (the square root of the variance). 3/17/2018 Compiled by F O Boateng 14

• The variance of returns is apparently the weighted sum of squared deviations from the expected returns. The reason for squaring the deviation is to ensure that both positive and negative deviations contribute equally to the measure of variability. Please consider the following worked example: 3/17/2018 Compiled by F O Boateng 15

RISK AND RETURN ON TWO-ASSET PORTFOLIOS. ILLUSTRATION • The following table gives information about four investments: A plc, B plc, C plc and D plc. Assume that the investor has decided to construct a two-asset portfolio and that he has already decided to invest 50% of the funds in A plc. He is currently trying to decide which one of the other three investments into which will invest the remaining 50% of his funds 3/17/2018 Compiled by F O Boateng 16
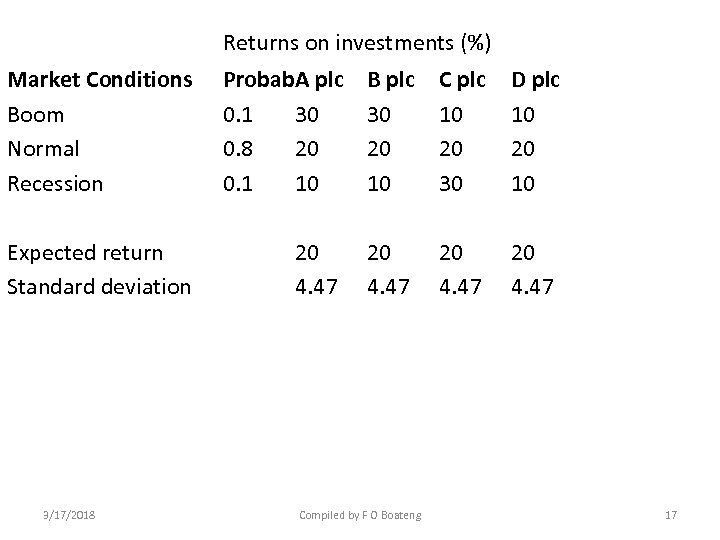
Returns on investments (%) Market Conditions Boom Normal Recession Probab. A plc 0. 1 30 0. 8 20 0. 1 10 B plc 30 20 10 C plc 10 20 30 D plc 10 20 10 Expected return Standard deviation 20 4. 47 3/17/2018 Compiled by F O Boateng 17

THE EXPECTED RETURN OF A TWO-ASSET PORTFOLIO This is computed as; Rport = XRA + (1 -x)RB, Where; x = the proportion of funds invested in A. (1 -x) = the proportion of funds invested in B. Therefore, Rport A+B = (0. 5 * 20) + (0. 5 * 20) = 20% Rport A+C = (0. 5 * 20) + (0. 5 * 20) = 20% Rport A+D = (0. 5 * 20) + (0. 5 * 20) = 20% The expected return of a two-asset portfolio (Rport) is simply the weighted average of the expected returns of the individual investments. 3/17/2018 Compiled by F O Boateng 18

Given from the above, the expected return is same for all portfolios, as such; the investor will opt for the portfolio that has the lowest risk as measured by the portfolios standard deviation 3/17/2018 Compiled by F O Boateng 19

THE STANDARD DEVIATION OF A TWO-ASSET PORTFOLIO • From the scenario above, the standard deviation of all individual investments is 4. 47%. Notably, you may think that it does not really matter which portfolio the investor chooses as the standard deviation of the portfolios should be the same (because the deviations of the individual investments are all same). 3/17/2018 Compiled by F O Boateng 20

• However, this analysis is completely out of gear! This is because a standard deviation of a portfolio (σport) is not simply the weighted average of the standard deviation of the individual investment but is generally less than the weighted average. 3/17/2018 Compiled by F O Boateng 21

• This effect is caused by the extent to which returns of the two investments co-vary or corelate (i. e. move up and down together), measured by using either covariance or correlation coefficient terms. 3/17/2018 Compiled by F O Boateng 22

• MEASURING COVARIABILITY Covariance (absolute measure) • Positive covariance indicates that the returns moves in the same direction • Negative covariance indicates that the returns move in opposite direction • Zero covariance indicates that the returns are independent of each other. 3/17/2018 Compiled by F O Boateng 23

• The formula for computing covariance is; Cova, b = ρa, bσaσb • Correlation coefficient is a relative mesaure of covariability • The formula for the standard deviation of returns of a two-asset portfolio is: (σport) = σa 2 x 2 + σb 2(1 x)2 + 2 X(1 -x) ρa, bσaσb 3/17/2018 Compiled by F O Boateng 24

• From the illustration above, (assuming the correlation coefficient of returns are; +1, 0, and -1 for portfolios - (A+B), (A+C) AND (A+D) respectively) then the portfolio risk for various combination of investment can be computed as folows; 3/17/2018 Compiled by F O Boateng 25

σport (A+B) = (4. 472 x 0. 52) + (2 x 0. 5) + 1(4. 47 x 4. 47) = 4. 47 σport (A+C) = (4. 472 x 0. 52) + (2 x 0. 5) – 1(4. 47 x 4. 47) = 0. 00 σport (A+D) = (4. 472 x 0. 52) + (2 x 0. 5) 0(4. 47 x 4. 47) = 3. 16 3/17/2018 Compiled by F O Boateng 26

• Summary ØThe expected return on a share comprises of a dividend yield and a capital gain/loss in percentage terms, ØThe required rate of return on a risky investment comprise the risk-free rate and risk premium, ØTotal risks is normally measured by the standard deviation of returns (σ), 3/17/2018 Compiled by F O Boateng 27

ØPortfolio theory demonstrates that it is possible to reduce risk without having a consequential reduction in return, i. e. the portfolio’s expected return is equal to the weighted average of the expected returns on the individual investments, whilst the portfolio risks is normally less than the weighted average of the risk of individual investments. 3/17/2018 Compiled by F O Boateng 28

• The extent of reduction is basically influenced by the way the returns on investments covary, normally measured by correlation coefficient, 3/17/2018 Compiled by F O Boateng 29

• A portfolios total risk consists of systematic and unsystematic risk. However, a well diversified portfolio suffers from systematic risk as the unsystematic risk has been diversified, 3/17/2018 Compiled by F O Boateng 30

MEASUREMENT OF SYSTEMATIC RISK • It is known that investors who hold welldiversified portfolios will find that the risk affecting the portfolio is wholly systematic. Unsystematic risk has been diversified away. These investors may want to measure the systematic risk of each individual investment within their portfolio, or of a potential new investment to be added to the portfolio. 3/17/2018 Compiled by F O Boateng 31

• A single investment is affected by both systematic and unsystematic risk but if an investor owns a well-diversified portfolio then only the systematic risk of that investment would be relevant. If a single investment becomes part of a welldiversified portfolio the unsystematic risk can be ignored. 3/17/2018 Compiled by F O Boateng 32

• The systematic risk of an investment is measured by the covariance of an investment's return with the returns of the market. • Once the systematic risk of an investment is calculated, it is then divided by the market risk, to calculate a relative measure of systematic risk. 3/17/2018 Compiled by F O Boateng 33

• This relative measure of risk is called the ‘beta' and is usually represented by the symbol b. If an investment has twice as much systematic risk as the market, it would have a beta of two. There are two different formulae for beta. The first is: 3/17/2018 Compiled by F O Boateng 34

3/17/2018 Compiled by F O Boateng 35

• You must commit both formulae to memory, as they are not given on the exam formulae sheet. The formula that you need to use in the exam will be determined by the information given in the question. If you are given the covariance, use the first formula or if you are given the correlation coefficient, use the second formula. 3/17/2018 Compiled by F O Boateng 36

• Example 2 You are considering investing in Y plc. The covariance between the company's returns and the return on the market is 30%. The standard deviation of the returns on the market is 5%. • Calculate the beta value: be = 30% = 1. 2 52% • 3/17/2018 Compiled by F O Boateng 37

• Example 3 You are considering investing in Z plc. The correlation coefficient between the company's returns and the return on the market is 0. 7. The standard deviation of the returns for the company and the market are 8% and 5% respectively. • Calculate the beta value: be = 0. 7 x 8% = 1. 12 5% 3/17/2018 Compiled by F O Boateng 38

• Investors make investment decisions about the future. Therefore, it is necessary to calculate the future beta. Obviously, the future cannot be foreseen. As a result, it is difficult to obtain an estimate of the likely future co-movements of the returns on a share and the market. 3/17/2018 Compiled by F O Boateng 39

• However, in the real world the most popular method is to observe the historical relationships between the returns and then assume that this covariance will continue into the future. You will not be required to calculate the beta value using this approach in the exam. 3/17/2018 Compiled by F O Boateng 40

• The CAPM Formula The capital asset pricing model (CAPM) provides the required return based on the perceived level of systematic risk of an investment: 3/17/2018 Compiled by F O Boateng 41

3/17/2018 Compiled by F O Boateng 42

• The calculation of the required return • Example 4 • The required return on a share will depend on the systematic risk of the share. What is the required return on the following shares if the return on the market is 11% and the risk free rate is 6%? 3/17/2018 Compiled by F O Boateng 43

• The shares in B plc have a beta value of 0. 5 Answer: 6% + (11% - 6%) 0. 5 = 8. 5% • The shares in C plc have a beta value of 1. 0 Answer: 6% + (11% - 6%) 1. 0 = 11% • The shares in D plc have a beta value of 2. 0 Answer: 6% + (11% - 6%) 2. 0 = 16%. 3/17/2018 Compiled by F O Boateng 44

• Obviously, with hindsight there was no need to calculate the required return for C plc as it has a beta of one and therefore the same level of risk as the market and will require the same level of return as the market, ie the RM of 11%. 3/17/2018 Compiled by F O Boateng 45

The meaning of beta • The CAPM contends that shares comove with the market. If the market moves by 1% and a share has a beta of two, then the return on the share would move by 2%. The beta indicates the sensitivity of the return on shares with the return on the market. Some companies' activities are 3/17/2018 Compiled by F O Boateng 46

more sensitive to changes in the market - eg luxury car manufacturers - have high betas, while those relating to goods and services likely to be in demand irrespective of the economic cycle - eg food manufacturers - have lower betas. The beta value of 1. 0 is the benchmark against which all share betas are measured 3/17/2018 Compiled by F O Boateng 47

• Beta > 1 - aggressive shares These shares tend to go up faster then the market in a rising (bull) market and fall more than the market in a declining (bear) market. • Beta < 1 - defensive shares These shares will generally experience smaller than average gains in a rising market and smaller than average falls in a declining market. 3/17/2018 Compiled by F O Boateng 48

• Beta = 1 - neutral shares These shares are expected to follow the market. • The beta value of a share is normally between 0 and 2. 5. A risk-free investment (a treasury bill) has a b = 0 (no risk). 3/17/2018 Compiled by F O Boateng 49

Basic exam application of CAPM • Capital investment decisions ØThe calculation of Ke in the WACC calculation to enable an NPV calculation • A shareholder's required return on a project will depend on the project's perceived level of systematic risk. 3/17/2018 Compiled by F O Boateng 50

• Different projects generally have different levels of systematic risk and therefore shareholders have a different required return for each project. A shareholder's required return is the minimum return the company must earn on the project in order to compensate 3/17/2018 Compiled by F O Boateng 51

• Example 5 E plc is evaluating a project which has a beta value of 1. 5. The return on the GSE All-Share Index is 15%. The return on treasury bills is 12%. • Required: What is the cost of equity? • Answer: 5% + (15% - 12%) 1. 5 = 9. 5% 3/17/2018 Compiled by F O Boateng 52

ØStock market investment decisions • When we read the financial section of newspapers, it is commonplace to see analysts advising us that it is a good time to buy, sell, or hold certain shares. The CAPM is one method that may employed by analysts to help them reach their conclusions. 3/17/2018 Compiled by F O Boateng 53

• An analyst would calculate the expected return and required return for each share. They then subtract the required return from the expected return for each share, ie they calculate the alpha value (or abnormal return) for each share. They would then construct an alpha table to present their findings. 3/17/2018 Compiled by F O Boateng 54

• Example 6 We are considering investing in F plc or G plc. Their beta values and expected returns are as follows: Beta values Expected returns F plc 1. 5 18% G plc 1. 1 18% The market return is 15% and the risk-free return is 5%. • Required: What investment advice would you give us? 3/17/2018 Compiled by F O Boateng 55
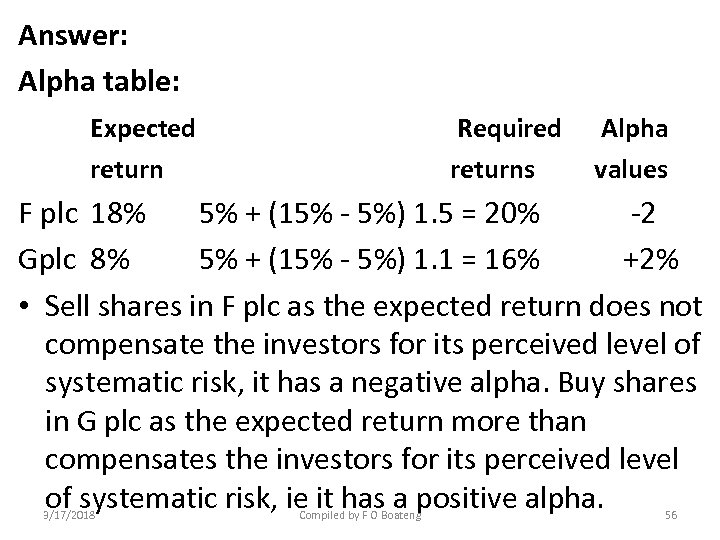
Answer: Alpha table: Expected Required returns return Alpha values F plc 18% 5% + (15% - 5%) 1. 5 = 20% -2 Gplc 8% 5% + (15% - 5%) 1. 1 = 16% +2% • Sell shares in F plc as the expected return does not compensate the investors for its perceived level of systematic risk, it has a negative alpha. Buy shares in G plc as the expected return more than compensates the investors for its perceived level of systematic risk, ie it has a positive alpha. 3/17/2018 Compiled by F O Boateng 56

ØThe preparation of an alpha table for a portfolio (the portfolio beta is a weighted average) A common exam-style question is a combined portfolio theory and CAPM question. A good example of this is the Boateng plc question at the end of this article where you are asked to calculate the alpha table for a portfolio. 3/17/2018 Compiled by F O Boateng 57

• The expected return of the portfolio is calculated as normal (a weighted average) and goes in the first column in the alpha table. We then have to calculate the required return of the portfolio. To do this we must first calculate the portfolio beta, which is the weighted average of the individual betas. Then we can calculate the required return of the portfolio using the CAPM formula. 3/17/2018 Compiled by F O Boateng 58

• Example 7 The expected return of the portfolio A + B is 20%. The return on the market is 15% and the risk-free rate is 6%. 80% of your funds are invested in A plc and the balance is invested in B plc. The beta of A is 1. 6 and the beta of b is 1. 1. • Required: Prepare the alpha table for the Portfolio (A + B) • Answer: • b(A + B) = (1. 6 ×. 80) + (1. 1 ×. 20) = 1. 5 • R portfolio (A + B) = 6% + (15% - 6%) 1. 5 = 19. 50% 3/17/2018 Compiled by F O Boateng 59

Alpha table Alpha value Expected return Required return Portfolio (A + B) 20% 19. 50% 0. 50% The Alpha Value If the CAPM is a realistic model (that is, it correctly reflects the risk-return relationship) and the stock market is efficient (at least weak and semi-strong), then the alpha values reflect a temporary abnormal return. In an efficient market, the expected and required returns are equal, ie a zero alpha. 3/17/2018 Compiled by F O Boateng 60

Investors are exactly compensated for the level of perceived systematic risk in an investment, ie shares are fairly priced. Arbitrage profit taking would ensure that any existing alpha values would be on a journey towards zero. . 3/17/2018 Compiled by F O Boateng 61

• Remember in Example 6 that the shares in G plc had a positive alpha of 2%. This would encourage investors to buy these shares. As a result of the increased demand, the current share price would increase, thus the expected return would fall. The expected return would keep falling until it reaches 16%, the level of the required return and the alpha becomes zero 3/17/2018 Compiled by F O Boateng 62

• The opposite is true for shares with a negative alpha. This would encourage investors to sell these shares. As a result of the increased supply, the current share price would decrease thus the expected return would increase until it reaches the level of the required return and the alpha value becomes zero. 3/17/2018 Compiled by F O Boateng 63

• It is worth noting that when the share price changes, the expected return changes and thus the alpha value changes. Therefore, it can be said that alpha values are as dynamic as the share price. Of course, alpha values may exist because CAPM does not perfectly capture the risk-return relationship due to the various problems with the model. 3/17/2018 Compiled by F O Boateng 64

Problems with CAPM 1. Investors hold well-diversified portfolios CAPM assumes that all the company's shareholders hold well-diversified portfolios and therefore need only consider systematic risk. However, a considerable number of private investors in the UK do not hold well-diversified portfolios. 2. One period model CAPM is a one period model, while most investment projects tend to be over a number of years. 3/17/2018 Compiled by F O Boateng 65

3. Assumes the stock market is a perfect capital market This is based on the following unrealistic assumptions: • no individual dominates the market • all investors are rational and risk-averse • investors have perfect information • all investors can borrow or lend at the riskfree rate • no transaction costs. 3/17/2018 Compiled by F O Boateng 66

4. Estimation of future b based on past b A scatter diagram is prepared of the share's historical risk premium plotted against the historical market risk premium usually over the last five years. The slope of the resulting line of best fit will be the b value. The difficulty of using historic data is that it assumes that historic relationships will continue into the future. This is questionable, as betas tend to be unstable over time. 3/17/2018 Compiled by F O Boateng 67

Exam style question • Boateng plc is considering investing in one of two short-term portfolios of four shortterm financial investments. The correlation between the returns of the individual investments is believed to be negligible (zero/independent/no correlation). See Portfolio 1 and Portfolio 2. The market return is estimated to be 15%, and the risk free rate 5%. 3/17/2018 Compiled by F O Boateng 68
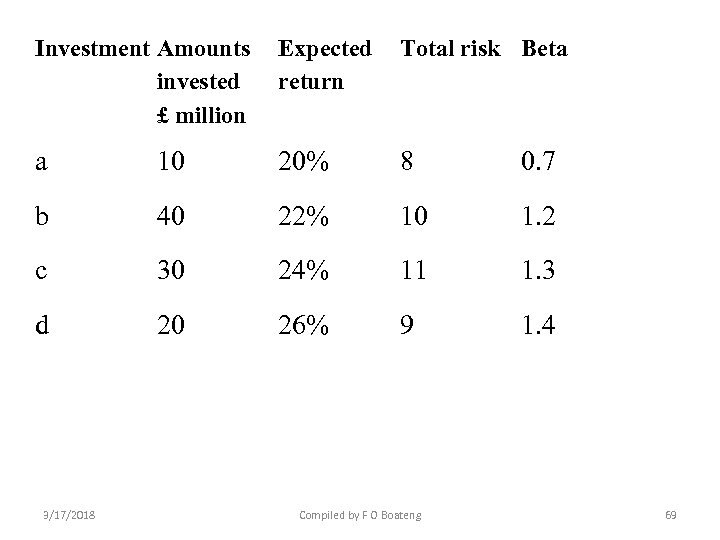
Investment Amounts Expected Total risk Beta invested return £ million a 10 20% 8 0. 7 b 40 22% 10 1. 2 c 30 24% 11 1. 3 d 20 26% 9 1. 4 3/17/2018 Compiled by F O Boateng 69
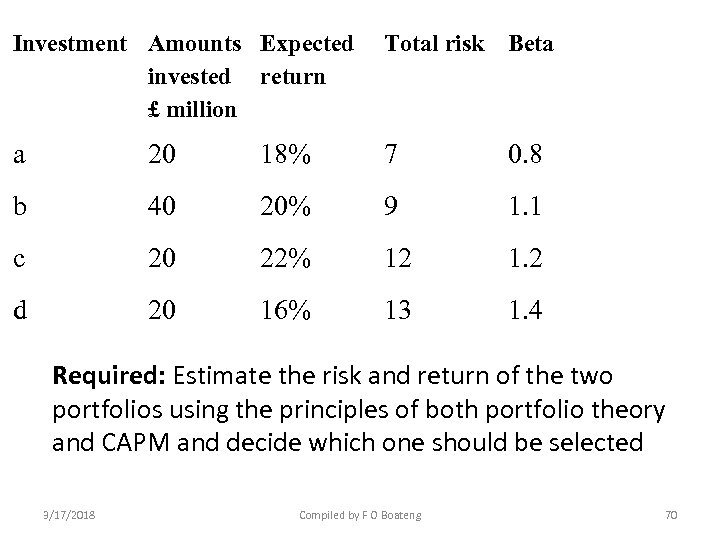
Investment Amounts Expected Total risk Beta invested return £ million a 20 18% 7 0. 8 b 40 20% 9 1. 1 c 20 22% 12 1. 2 d 20 16% 13 1. 4 Required: Estimate the risk and return of the two portfolios using the principles of both portfolio theory and CAPM and decide which one should be selected 3/17/2018 Compiled by F O Boateng 70

Answer The CAPM calculations - the application of CAPM principles in the exam means the preparation of the alpha table to find the portfolio with the largest positive alpha. See Portfolio 1 Solution and Portfolio 2 Solution. 3/17/2018 Compiled by F O Boateng 71
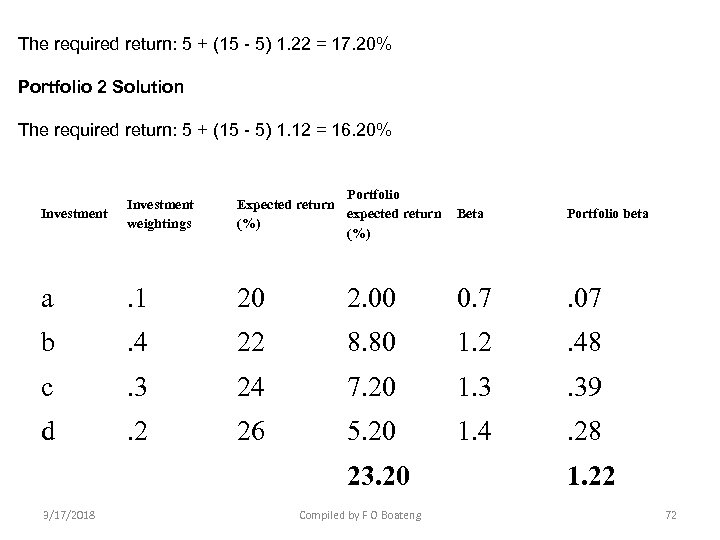
The required return: 5 + (15 - 5) 1. 22 = 17. 20% Portfolio 2 Solution The required return: 5 + (15 - 5) 1. 12 = 16. 20% Investment weightings Portfolio Expected return expected return Beta (%) Portfolio beta a . 1 20 2. 00 0. 7 . 07 b . 4 22 8. 80 1. 2 . 48 c . 3 24 7. 20 1. 3 . 39 d . 2 26 5. 20 1. 4 . 28 23. 20 1. 22 3/17/2018 Compiled by F O Boateng 72
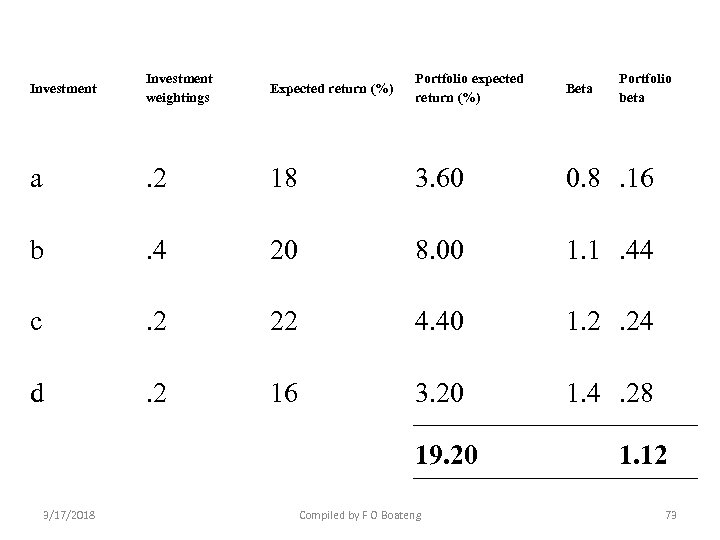
Investment weightings Expected return (%) Portfolio expected return (%) Beta a . 2 18 3. 60 0. 8 . 16 b . 4 20 8. 00 1. 1. 44 c . 2 22 4. 40 1. 2. 24 d . 2 16 3. 20 1. 4 . 28 19. 20 3/17/2018 Compiled by F O Boateng Portfolio beta 1. 12 73

Alpha table: Expected returns Required returns Alpha values Portfolio 1 23. 20% 17. 20% 6. 00% Portfolio 2 19. 20% 16. 20% 3. 00% Portfolio 1 is chosen because it has the largest positive alpha 3/17/2018 Compiled by F O Boateng 74

Key issues: 1. The beta is a relative measure of systematic risk. It indicates the sensitivity of the return on a share with the return on the market. If the market moves by 1% and a share has a beta of two, then the return on the share would move by 2%. 2. We may have to calculate the beta from basic data using the following two different formulae: 3/17/2018 Compiled by F O Boateng 75

3. Ensure that you know how to calculate the required return using the CAPM formula: Required Return = RF + (RM - RF) beta 3/17/2018 Compiled by F O Boateng 76
521464e59d816678bcb519cfd18c93fb.ppt