Risk Mitigation Services for Ads Hubert Jin, Jinsong Tan
Motivation • Hedge against the fluctuation of bids for sponsored ads. • Risk sharing and budget control on future sponsored ads cost. • Opportunity for speculation - win or lose. • Secondary market for sponsored ads.
Risk Sharing Models • Guaranteed slot (premium, deductible) – Is it possible ? • Number of slots is limited. • Insurance (premium, deductible, limit) – Customers may be fooled. • Two policies with limits of $5. 00 and $5. 01. • Co-pay (premium, deductible, co-pay rate) – Risk is shared, not 100% mitigated.
Advantages of Co-pay Model • It prevents irrational bidding of those who purchase policies (risk mitigation service). • Those who purchase policies are more likely to win the bids, which forces the rest to participate in risk mitigation. • Unlimited policies can be sold on limited ads slots. • Policies can be trade at exchange market.
Valuation • Borrow ideas from Black-Scholes of the stock option market. • Historical data provides trends and the variability of the bids. • Speculation activities on the exchange market will ‘likely’ to bring the valuation right. • Equilibrium of bids with risk mitigation.
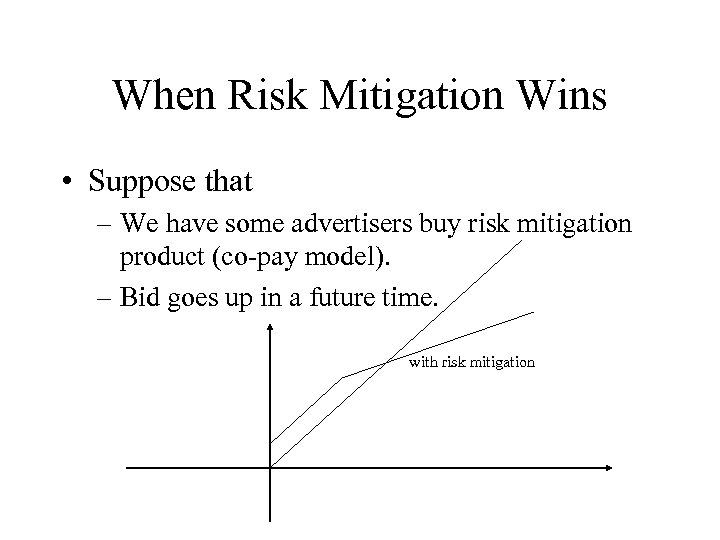
When Risk Mitigation Wins • Suppose that – We have some advertisers buy risk mitigation product (co-pay model). – Bid goes up in a future time. with risk mitigation
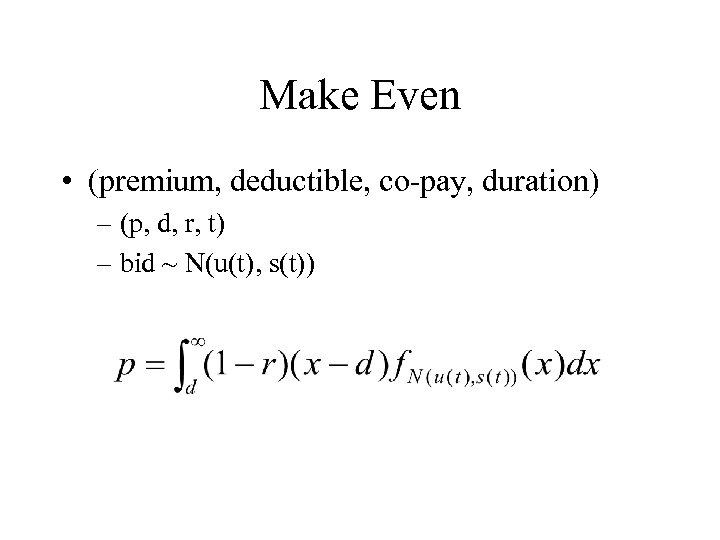
Make Even • (premium, deductible, co-pay, duration) – (p, d, r, t) – bid ~ N(u(t), s(t))
Equilibrium With Risk Mitigation • No risk mitigation. – Google/Yahoo take all the money on the table. • Bidders escalate the bids. • Except for those bidder whose limits are too low to compete. • With risk mitigation (assume it is offered by the auctioneer) – The risk mitigation mechanism could force bidders to buy risk mitigation service which also drives up bids. – Auctioneer also collects money from bidders who purchase risk mitigation contracts but withdraw when bids are too high.
Black-Scholes • The price of the underlying instrument S_t follows a geometric Brownian motion with constant drift and volatility: – – – d. S_t = mu S_t dt + sigma S_t d. W_t It is possible to short sell the underlying stock. There are no arbitrage opportunities. Trading in the stock is continuous. There are no transaction costs or taxes. All securities are perfectly divisible (e. g. it is possible to buy 1/100 th of a share). – It is possible to borrow and lend cash at a constant risk-free interest rate.
Black-Scholes (continue)
Скачать презентацию Risk Mitigation Services for Ads Hubert Jin Jinsong
ed45bf9cec10ddd5c6c1e088682a7c2b.ppt