Risk Management Lectures 6 7 8 i

Risk Management Lectures 6, 7 & 8 (i) Fixed Income Securities (ii) Interest Rate Sensitivity (iii) Duration & Convexity Nadir Khan

Risk Management Fixed Income Terminologies • We frequently refer to fixed income securities as bonds. • A zero coupon bond (or zero) promises a single cash flow, face value (or par value) at some future date, maturity. • A coupon bond promises a periodic cash flow, coupon and the face value at maturity. The coupon rate is the ratio of the coupon to the face value. Coupon payments are typically semiannual for US bonds and annual for European bonds. • The time to maturity is the length of time until maturity. • For notational simplicity, we assume from now on that bonds have a face value of $100. This is equivalent to expressing bond prices as a percentage of face value. Nadir Khan

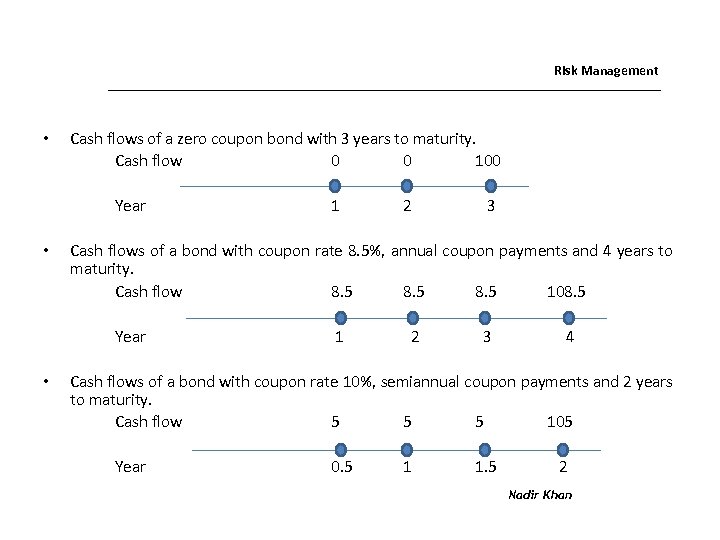Risk Management • Cash flows of a zero coupon bond with 3 years to maturity. Cash flow 0 0 100 Year • 2 3 Cash flows of a bond with coupon rate 8. 5%, annual coupon payments and 4 years to maturity. Cash flow 8. 5 108. 5 Year • 1 1 2 3 4 Cash flows of a bond with coupon rate 10%, semiannual coupon payments and 2 years to maturity. Cash flow 5 5 5 105 Year 0. 5 1 1. 5 2 Nadir Khan

Risk Management Treasury Securities • Fixed income securities generally involve default risk, the risk that the issuer will not meet the cash flow obligations. • The only fixed income securities that involve virtually no default risk are US Treasury Securities. We will focus on these securities because they are the simplest to value. • The Treasury issues have three types of securities: – Treasury Bills (T-Bills): Maturities up to 1 year. No coupon. – Treasury Notes (T-Notes): Maturities between 1 and 10 years. Semiannual coupon. – Treasury Bonds (T-Bonds): Maturities greater than 10 years. Semiannual coupon. • The Treasury allows buyers of T-Notes and T-Bonds to exchange them for the individual coupons and face value. These zero coupon bonds can be traded and are called Treasury Strips (T-Strips). Nadir Khan

Risk Management Term Structure • • • To value fixed income securities, it is essential to know the spot rate for each maturity. The term structure of spot rates (or yield curves) represents the spot rates as a function of maturity. The term structure can have many shapes: – It is generally upward sloping. This means that spot rates for long maturities are generally higher than those for short maturities. – However, it can also be hump shaped, inverted hump shaped, or downward sloping. – Upward sloping term structures are associated with periods of economic expansion. – Downward sloping term structures are associated with periods of economic slowdown/recession. • Spot rates, both for short and long maturities move substantially over time. Nadir Khan

Risk Management Valuation of Fixed Income Securities Zero Coupon Bonds Consider a zero coupon bond with T years to maturity. The PV of the bond’s cash flows will be: 100 PV = (1 + r. T)t Where: r. T = T year spot rate. T = Time period/maturity PV = Present value/Price of the bond • • • A zero coupon bond is always sold at “discount” below face value. Nadir Khan

Risk Management Valuation of Fixed Income Securities (cont’d …) Coupon Bonds • Consider a bond with annual coupon rate c% (i. e. , annual coupon payments of c) and T years to maturity. • The PV of the bond’s cash flows will be: c c 100 + c PV = + + ……. . + (1+r 1) (1+r 2)2 (1+r. T)T • A coupon bond may sell at discount (below face value), at par (at face value) or at premium (above face value). Nadir Khan

Risk Management Valuation of Fixed Income Securities • Consider a bond with semiannual coupon rate c%, (i. e. , semiannual coupon payments of c/2) and T years to maturity. Assume that the spot rates are quoted as semiannual APRs. • The PV of the bond’s cash flows will be: c/2 100 + c/2 PV = + + (1+r 0/2) (1+r 1/2)2 (1+r. T/2)T Nadir Khan

Risk Management Obtaining Spot Rates • • So far, we took the spot rates as given. But how can we obtain them? Recall that the price of a zero coupon bond with T years to maturity is: 100 = 100 x d. T (1+r)T • Therefore, we can obtain: – The discount factor d. T, by dividing the price by 100. (d. T = Price / 100) – The T year spot rate, by 1 d. T = (1 + r)T 1 = r. T = 1/T d. T Nadir Khan 1

Risk Management Valuation via Zero Coupon Bonds : An Example • • Consider a coupon bond with annual coupon rate 10% and 3 years to maturity. Cash flows are Cash flow 10 10 110 Year • • 1 2 3 Suppose that the prices of zero coupon bonds with maturities 1, 2 and 3 years are 95, 88 and 80 respectively. The price of the coupon bond is: Price = 10 x d 1 + 10 x d 2 + 110 x d 3 = 10 x 0. 95 + 10 x 0. 88 + 110 x 0. 8 = 106. 3 Nadir Khan

Risk Management Yield to Maturity (YTM) • The YTM of a bond is the discount rate that equates the PV of the bond’s cash flows to the bond’s price. • Viewing the bond as an “investment project, ” the YTM is simply the bond’s IRR. • For a bond with annual coupon rate c% and T years to maturity, the YTM (y) is given by: c c 100 + c Price = + + ……. . + (1+y)2 (1+y)T Nadir Khan

Risk Management Facts about YTM The relation between a bond’s YTM and coupon rate tells us how the bond’s price compares to the face value. • If the YTM is greater than the coupon rate, then the bond sells at discount (below face value) • If the YTM is equal to the coupon rate, then the bond sells at par (at face value) • If the YTM is less than the coupon rate, then the bond sells at premium (above face value) Nadir Khan

Risk Management Uses of YTM • Main uses of YTM are: – A measure of bond’s return. – A tool for choosing between different bonds. Nadir Khan

Risk Management YTM and Return: Zero-Coupon Bonds • • • The YTM of a zero-coupon bond is the spot rate corresponding to the bond’s time to maturity. This is the return of investing in the bond and holding it until maturity. But it is not the return for any other investment horizon. Example: consider a zero-coupon bond with 3 years to maturity and YTM 6%. The return of investing in the bond and holding it for 3 years is 6%. However, the return of investing in the bond and selling it after one year is unknown today. – The return depends on the bond’s price next year. – The price next year depends on the 2 year spot rate that will prevail next year. This spot rate is unknown today. Nadir Khan

Risk Management YTM and Return: Coupon Bonds • The YTM of a coupon bond is the return of investing in the bond, holding it until maturity and reinvesting the coupons at a rate to the YTM. • The YTM is not the return for any investment horizon other than maturity. This is for the same reason as for zero-coupon bonds. • The YTM is not the return even for investment horizon equal to maturity. This is because the future spot rates at which coupons will be reinvested may be different than the YTM. Nadir Khan

Risk Management The YTM as a Tool for Comparing Bonds • Using the YTM for comparing bonds is correct only when the bonds have the same coupon and time to maturity. In all other cases it can be very misleading. • Suppose, for instance, that the bonds have different time to maturity: – Recall that the YTM is at best the return of investing until maturity. – Therefore, by comparing YTMs we compare returns for different investment horizons. • The correct way to compare bonds is simply to compute the PV of their cash flows. Nadir Khan

Risk Management 1 st Basic Fact about Interest Rates • Bond prices are sensitive to interest rate movements. They go down when interest rates go up and vice versa. • Bond prices are negatively related to interest rates. • Bond prices are the PV of bonds cash flows. If interest rates go up, cash flows are discounted more heavily and the PV goes down. • Suppose that interest rates go up. Investors will sell bonds in order to invest in the higher interest rates. Therefore, bonds prices will decrease. Nadir Khan

Risk Management 2 nd Basic Fact about Interest Rates • Prices of long term bonds are more interest rate sensitive than prices of intermediate term bonds. • The interest rate sensitivity of bond prices increases with maturity. • The cash flows of long term bonds are farther in the future, and are more heavily discounted than the cash flows of short term bonds. • Therefore, the PV of the cash flows is more interest rate sensitive for long term bonds than for short term bonds. Nadir Khan

Risk Management Measuring and Managing Interest Rate Risk • We showed that interest rate risk is important and impacts bond prices. • Many market participants need to measure and manage interest rate risk. – – Bonds Banks Pension Funds Insurance Companies etc. • Interest Rate Risk can be measured and managed by using Duration and Convexity. Nadir Khan

Risk Management Performance Profile • To define duration and convexity, we first need to define an important curve, the Performance Profile. • For simplicity, we assume that interest rates are independent of maturity. This means that the term structure is flat. • With a flat term structure, interest rate movements can only be parallel shifts in the term structure. Nadir Khan

Risk Management Defining the Performance Profile • Consider a bond with annual coupon rate c% and T years to maturity. • Consider an investment in the bond, worth $1 at the current interest rate r. determine value of the investment when interest rate moves to r + Δr. – Price of the bond at r: P(r) = c (1+r)1 + c (1+r)2 +…+ – Units of the bond that can be bought with $1 at r: – Value of the investment r + Δr: P(r + Δr) 100 + c (1+r)n 1 P(r) Nadir Khan

Risk Management Defining the Performance Profile • We can plot the value of the investment as a function of the interest rate r + Δr. • This curve is the performance profile of the bond. • Duration and Convexity are based on the performance: – Duration is related to the slope of the performance profile. – Convexity is related to the curvature of the performance profile. Nadir Khan

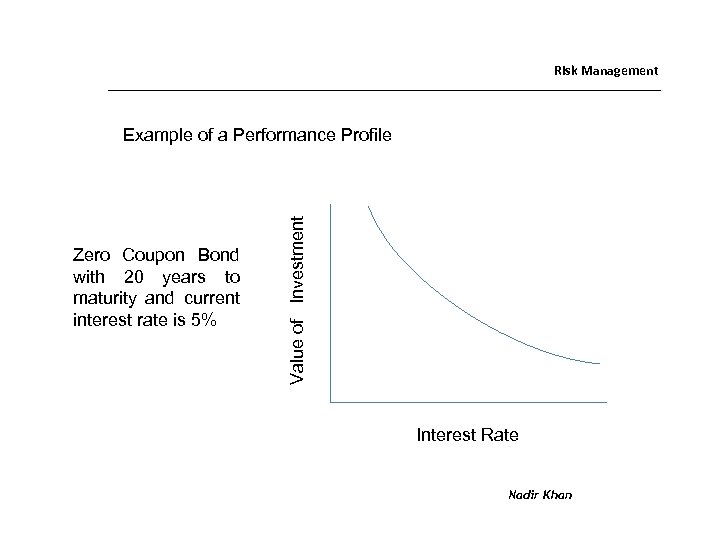Risk Management Zero Coupon Bond with 20 years to maturity and current interest rate is 5% Value of Investment Example of a Performance Profile Interest Rate Nadir Khan

Investment Analysis Some Important Points • The performance profile is downward sloping. The value of the investment goes down when interest rates go up. • The performance profile is convex. The value goes down at a decreasing rate. • These conclusions hold for any standard bond. Nadir Khan

Risk Management Conclusions • The slope of the performance profile increases with maturity. • The slope of the performance profile decreases with coupon rate. Nadir Khan

Risk Management Duration • Duration is related to the slope of the performance profile, at the current interest rate r. • Two concepts of duration: – Macaulay duration (D). – Modified duration (D*). Nadir Khan

Risk Management Macaulay Duration (D) • It is the weighted average of payback period of a bond / weighted average of the years in which the bond pays cash flows. • Consider a bond with annual coupon rate c% and T years to maturity. • The Macaulay Duration (D) of the bond is: D = Where, n x DCF Price of Bond n = year / time period DCF = discounted cash flows Nadir Khan

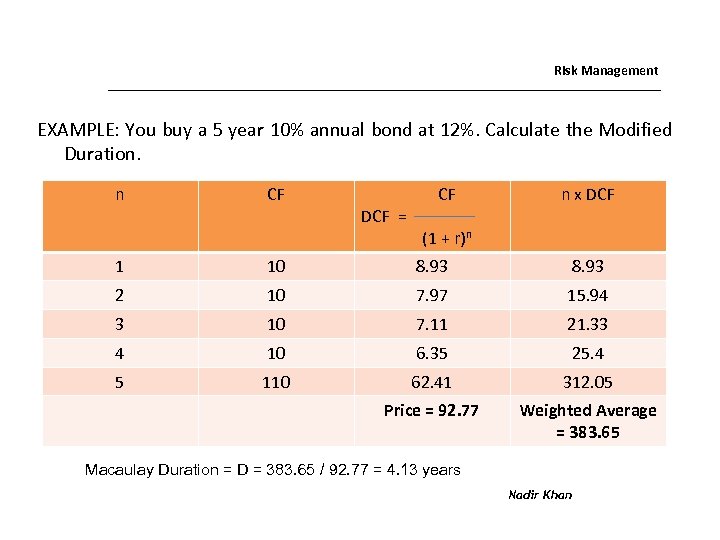Risk Management EXAMPLE: You buy a 5 year 10% annual bond at 12%. Calculate the Modified Duration. n CF DCF = CF n x DCF (1 + r)n 1 10 8. 93 2 10 7. 97 15. 94 3 10 7. 11 21. 33 4 10 6. 35 25. 4 5 110 62. 41 312. 05 Price = 92. 77 Weighted Average = 383. 65 Macaulay Duration = D = 383. 65 / 92. 77 = 4. 13 years Nadir Khan

Risk Management Modified Duration = D* = 1 1+r 1 1. 12 x Macaulay Duration x 4. 13 3. 68 years Nadir Khan

Risk Management Macaulay Duration • Macaulay duration can be interpreted as a “center of gravity. ” It is the year around which the bond’s discounted cash flows are balanced. • The Macaulay duration is, in a sense, the effective maturity of the bond. • Macaulay duration is a measure of maturity and the slope of the performance profile depends on maturity, therefore, in this manner a link between the Macaulay duration and slope of the Performance profile can be expected. Nadir Khan

Risk Management Macaulay Duration: Properties • For a zero coupon bond with T years to maturity, D = T. • D generally increases with increase in time to maturity (but not always). • D always decreases with the increase in coupon rate. Nadir Khan

Risk Management Modified Duration • D* = 1 1+r x Macaulay Duration • D* is the % change in price given % change in interest rate. • It shows sensitivity to interest rate risk. • The slope of the performance profile, at the current interest rate r is D*. Nadir Khan

Risk Management Using Duration: A Preview • So far: – We defined D and D*. – We showed that the slope of the performance profile, at the current interest rate r, is D*. • But how can we use D and D*? • Consider an investment in the bond, which is worth P at the current interest rate r. • We can use D and D* to approximate the change in the investment’s value as interest rates change. • We can approximate the change in the investment’s value using the slope of the investment’s performance profile. Nadir Khan

Risk Management Using Duration: A Preview (cont’d …) – The slope of the performance profile of a $1 investment is D*. – Therefore, the slope of the performance profile of an investment worth P is PD*. – For a small interest rate movement Δr, the change in the investment’s value is approximately: ΔP ≈ - PD* Δr Nadir Khan

Risk Management • EXAMPLE A bond with annual coupon rate 6% and 20 years to maturity. Current interest rate r = 5%. • Price of the bond is P = 112. 46 • Macaulay duration is 12. 62 and modified duration is 12. 02 • Suppose that interest rate goes up to 5. 1%. – Price of the bond becomes 111. 12 and exact change in bond price is: ΔP = 111. 12 - 112. 46 = -1. 34 – Approximate change in bond price is: ΔP ≈ -PD*Δr =(-112. 46)(12. 02)(0. 1%) = -1. 35 Nadir Khan

Risk Management EXAMPLE (cont’d …) • Now suppose the interest rate goes down to 4. 9% Exact change: Approximate change: ΔP = 1. 36 ΔP = 1. 35 • For small shifts in the term structure, duration provides a good approximation to the actual change. • Now suppose the interest rate change is 0. 5% (up to 5. 5% or down to 4. 5%). Exact change: Approximate change: • ΔP = -6. 49 for an upward shift ΔP = 7. 05 for a downward shift ΔP = -6. 76 for upward shift ΔP = 6. 76 for a downward shift For large shifts in the term structure, duration provides a less precise approximation to the actual change. Nadir Khan

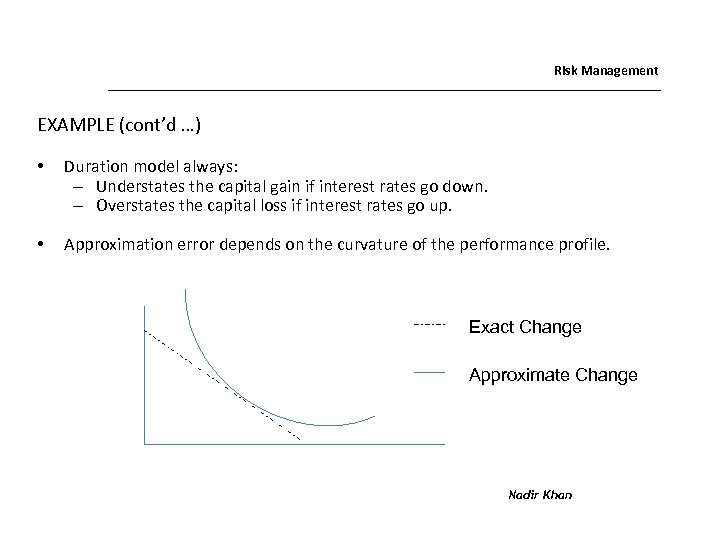Risk Management EXAMPLE (cont’d …) • Duration model always: – Understates the capital gain if interest rates go down. – Overstates the capital loss if interest rates go up. • Approximation error depends on the curvature of the performance profile. Exact Change Approximate Change Nadir Khan

Risk Management Convexity • For any given bond, a graph of the relationship between price and yield is convex. • This means that the graph forms a curve rather than a straight-line (linear). • The degree to which the graph is curved shows how much a bond’s yield changes in response to a change in price. • In this section we take a look at what affects convexity and how investors can use it to compare bonds. Nadir Khan

Risk Management Convexity (cont’d …) • We use convexity (in addition to duration) in order to better approximate the change in an investment’s value. • Convexity is related to the curvature of the performance profile, at the current interest rate r. The convexity (г) of a bond with annual coupon rate c% and T years to maturity is: 1 T г= ∑ wtt(t+1) (1+r)2 t=1 Where (wt) shows the weights. • • Fact: The curvature of the performance profile, at the current interest rate r, is г. • For a small interest rate movement r, the change in an investment’s value is approximately: ΔP = - PD* Δ r + ½ P г(Δ r)2 Nadir Khan

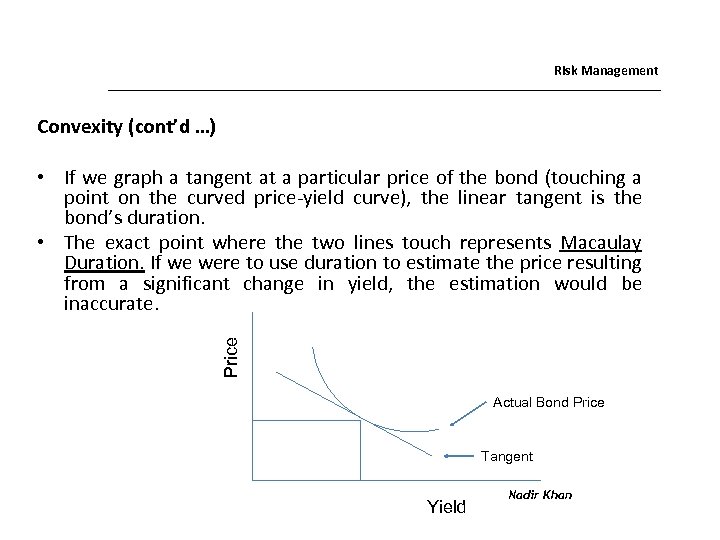Risk Management Convexity (cont’d …) Price • If we graph a tangent at a particular price of the bond (touching a point on the curved price-yield curve), the linear tangent is the bond’s duration. • The exact point where the two lines touch represents Macaulay Duration. If we were to use duration to estimate the price resulting from a significant change in yield, the estimation would be inaccurate. Actual Bond Price Tangent Yield Nadir Khan

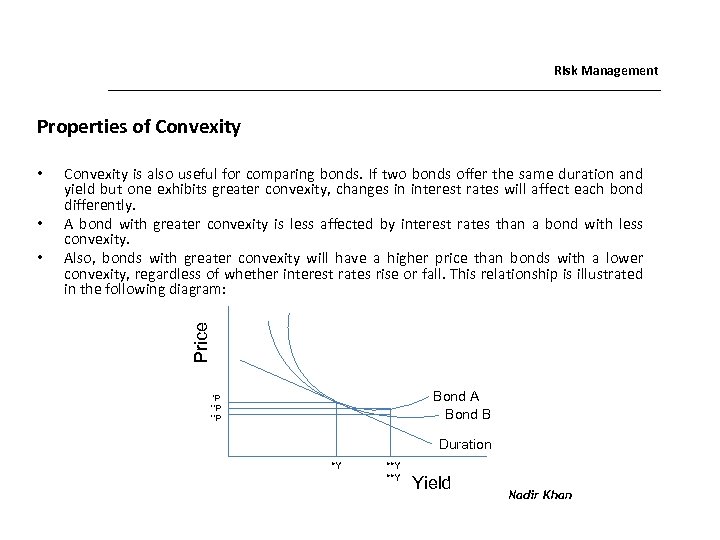Risk Management Properties of Convexity • • Convexity is also useful for comparing bonds. If two bonds offer the same duration and yield but one exhibits greater convexity, changes in interest rates will affect each bond differently. A bond with greater convexity is less affected by interest rates than a bond with less convexity. Also, bonds with greater convexity will have a higher price than bonds with a lower convexity, regardless of whether interest rates rise or fall. This relationship is illustrated in the following diagram: Price • Bond A Bond B *P **P Duration *Y **Y Yield Nadir Khan

Risk Management Properties of Convexity (cont’d …) • As you can see that Bond A had greater convexity than Bond B but they both have the same price and convexity when price equals *P and yield equals *Y. • If interest rates change from this point by a very small amount, then both bonds would have approximately the same price, regardless of the convexity. • When yield increases by a large amount, however, the prices of both Bond A and Bond B decrease but Bond B’s price decreases more than Bond A’s. • Notice how at **Y the price of Bond A remains higher, demonstrating that investors will have to pay more money (accept a lower yield to maturity) for a bond with greater convexity. Nadir Khan

Risk Management Why Hedge? A Preview • Hedgers are interested in reducing a risk that they already face. • Example: An investment bank sold a complicated (fixed-income) instrument to a client. Client: – Bears the instrument specific risk. Investment Bank: – Owes the instrument. – Bears the counterparty risk. • Market participants may be averse to big losses. Nadir Khan

Risk Management Approaches Risk Managers may want to: • Fully offset (hedge) all existing risk – Balance Sheet immunization • Approximately offset all existing risk – Duration and duration-convexity models • Control the downside – Portfolio Insurance: under no circumstances can the value of a portfolio drop below the floor $K. – Value –at-Risk: the probability that the value of a portfolio drops below the floor $K may not exceed 1%. Nadir Khan

Risk Management Using Duration • Market participants need to measure the sensitivity of their net worth to interest rate movements. • Duration provides a simple, convenient measure. • Market participants can sometimes control (or manage) the interest rate sensitivity of their net worth. They can do this by changing the composition of their assets or liabilities. • Duration is a useful tool for managing interest rate risk. Nadir Khan

Risk Management Managing Interest Rate Risk: An Example • You are the CFO of an insurance company. Your liabilities consist of four $20 million payments in 14, 15, 17 and 18 years. Your assets consist of $ 35 million. You are uncertain about future interest rates and would like to immunize your net worth (i. e. , make it insensitive to interest rate movements). What should you do? Nadir Khan

Risk Management A Dangerous Choice • Suppose you keep the $35 million in cash. • Suppose the current interest rate is 6%. – The PV of your liabilities is: 20 20 L = + + + = 31. 63 million 14 15 17 18 (1+6%) – Your net worth is: A – L = 35 – 31. 63 = 3. 37 million • Suppose the interest rate moves to 5%. – The PV of your liabilities becomes: 20 20 L = + + (1+5%)14 (1+5%)15 – Your net worth becomes: 20 (1+5%)17 + 20 (1+5%)18 = - 1. 76 million A – L = 35 – 36. 76 = - 1. 76 million Nadir Khan