RIEMANNIAN GEOMETRY CRITERION FOR CLASSICAL CHAOS Pavel Stránský

RIEMANNIAN GEOMETRY CRITERION FOR CLASSICAL CHAOS Pavel Stránský www. pavelstransky. cz Instituto de Ciencias Nucleares, Universidad Nacional Autónoma de México In collaboration with: Pavel Cejnar Institute of Particle and Nuclear Phycics, Faculty of Mathematics and Physics, Charles University in Prague, Czech Republic Michal Macek Racah Institute of Physics, The Hebrew University, Jerusalem, Israel XLIII Escuela Latino Americana de Física, 1 a ”Marcos Moshinsky“, Colegio Nacional, México 30 th July 2013

1. Geometrical Method - flat X curved space (embedding of a Hamiltonian system with a potential in a flat space into a curved space with a Riemannian tensor) 2. Model - classical dynamics of the Geometric Collective Model (GCM) of atomic nuclei 3. Results and discussion - full map of classical chaos in the GCM - instability predicted by the Geometrical method - relation between the Geometrical method and the shape of equipotential surfaces

1. Geometrical Method for Hamiltonian systems

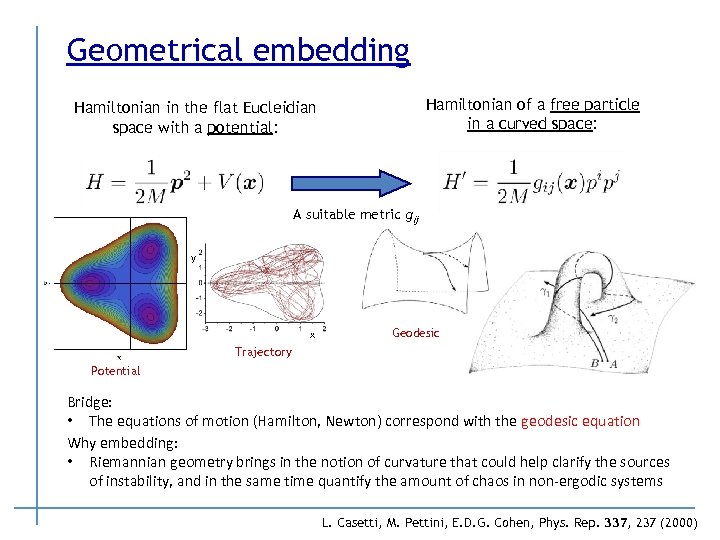Geometrical embedding Hamiltonian of a free particle in a curved space: Hamiltonian in the flat Eucleidian space with a potential: A suitable metric gij y x Geodesic Trajectory Potential Bridge: • The equations of motion (Hamilton, Newton) correspond with the geodesic equation Why embedding: • Riemannian geometry brings in the notion of curvature that could help clarify the sources of instability, and in the same time quantify the amount of chaos in non-ergodic systems L. Casetti, M. Pettini, E. D. G. Cohen, Phys. Rep. 337, 237 (2000)

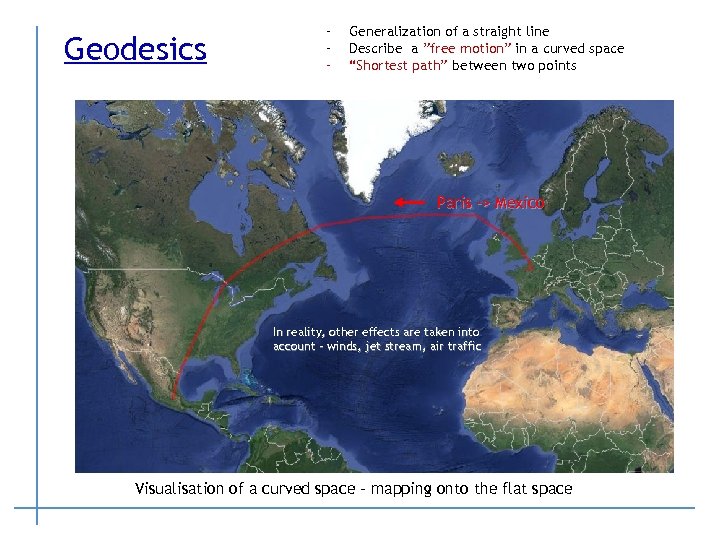Geodesics - Generalization of a straight line Describe a ”free motion” in a curved space “Shortest path” between two points Paris -> Mexico In reality, other effects are taken into account – winds, jet stream, air traffic Visualisation of a curved space - mapping onto the flat space

Flat space Curved space (dynamics) (geometry) Potential energy Time Forces Curvature of the potential Metric Arc-length Christoffel’s symbols Riemannian tensor Ricci tensor Scalar curvature Trajectories Hamiltonian equations of motion Geodesics Geodesic equation Tangent dynamics equation Equation of the geodesic deviation (Jacobi equation) Lyapunov exponent

Choice of the metric M. Pettini, Geometry and Topology in Hamiltonian Dynamics and Statistical Mechanics, Springer, New York, 2007 1. Jacobi metric - conformal metric - arc-length - nonzero scalar curvature (negative only when DV < 0) 2. Eisenhart metric - space with 2 extra dimensions - arc-length equivalent with time - only one nonzero Christoffel’s symbol and vanishing scalar curvature 3. Israeli metric (Horwitz et al. ) - conformal metric - arc-length proportional to time - metric incompatible connection form metric compatible connection L. Casetti, M. Pettini, E. D. G. Cohen, Phys. Rep. 337, 237 (2000) L. Horwitz et al. , Phys. Rev. Lett. 98, 234301 (2007)

Curvature and instability Besides solving the equation for the geodesic deviation, can one deduce something about the instability only from the curvature? 1. Riemannian tensor Difficult, the number of components grows with the 4 th power of dimension 2. Scalar curvature • R = const (isotropic manifold) • R<0 • Equation of the geodetic deviation stable R > 0 Equation of motion for • harmonic oscillator with frequency • exponential divergence with Lyapunov exponent unstable R>0 Unstable motion with estimated Lyapunov exponent dim = 2 Equation of motion of a harmonic oscillator with its length (stiffness) modulated in time Unstable if the frequency is in resonance with any of the frequency of the Fourier expansion, even if R(s) > 0 on the whole manifold: Parametric instability

Curvature and instability Besides solving the equation for the geodesic deviation, can one deduce something about the instability only from the curvature? 3. Israeli method Using the Israeli metric and connection form, the equation of the geodesic deviation is expressed as - projector into a direction orthogonal to the velocity Stability matrix Conjecture: A negative eigenvalue of the Stability matrix inside the kinematically accessible area induces instability of the motion. Example of unstable configuration Kinematically accessible area Negative lower eigenvalue of V Negative higher eigenvalue of V L. Horwitz et al. , Phys. Rev. Lett. 98, 234301 (2007)

2. Model (Geometric collective model of nuclei)

Hamiltonian It describes: Collective motion of an atomic nucleus (Bohr model) … but also (for example): Motion of a star around a galactic centre, assuming the motion is cylindrically symmetric (Hénon-Heiles model)

Geometric collective model Surface of homogeneous nuclear matter: (even-even nuclei – collective character of the lowest excitations) Monopole deformations l = 0 - “breathing” mode - Does not contribute due to the incompressibility of the nuclear matter Dipole deformations l = 1 - Related to the motion of the center of mass - Zero due to momentum conservation

Geometric collective model Surface of homogeneous nuclear matter: Quadrupole deformations l = 2 Corresponding tensor of momenta Quadrupole tensor of collective coordinates (2 shape parameters, 3 Euler angles) T…Kinetic term V…Potential Neglect higher order terms neglect 4 external parameters G. Gneuss, U. Mosel, W. Greiner, Phys. Lett. 30 B, 397 (1969)

Geometric collective model Surface of homogeneous nuclear matter: Quadrupole deformations l = 2 Corresponding tensor of momenta Quadrupole tensor of collective coordinates (2 shape parameters, 3 Euler angles) T…Kinetic term V…Potential Neglect higher order terms neglect 4 external parameters Scaling properties 1 “shape” parameter (order parameter) Adjusting 3 independent scales energy (Hamiltonian) size (deformation) time 1 “classicality” parameter sets absolute density of quantum spectrum (irrelevant in classical case) P. Stránský, M. Kurian, P. Cejnar, Phys. Rev. C 74, 014306 (2006)

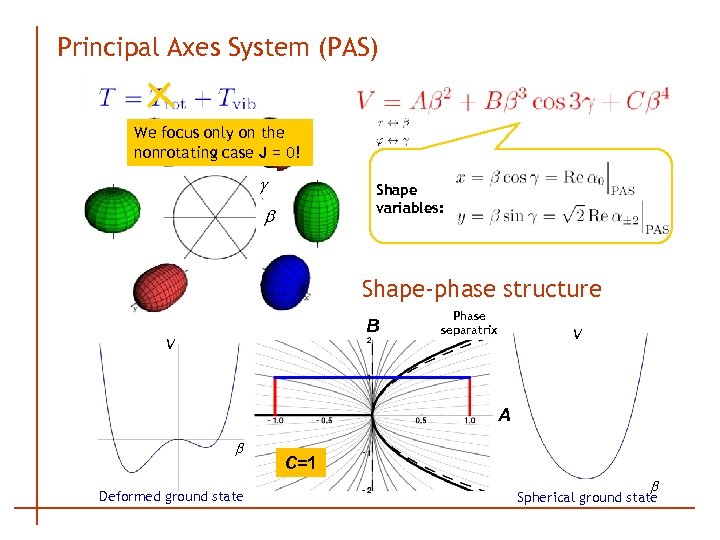Principal Axes System (PAS) We focus only on the nonrotating case J = 0! g Shape variables: b Shape-phase structure B V Phase separatrix V A b Deformed ground state C=1 b Spherical ground state

3. Results and discussion (Israeli geometry method applied to GCM)

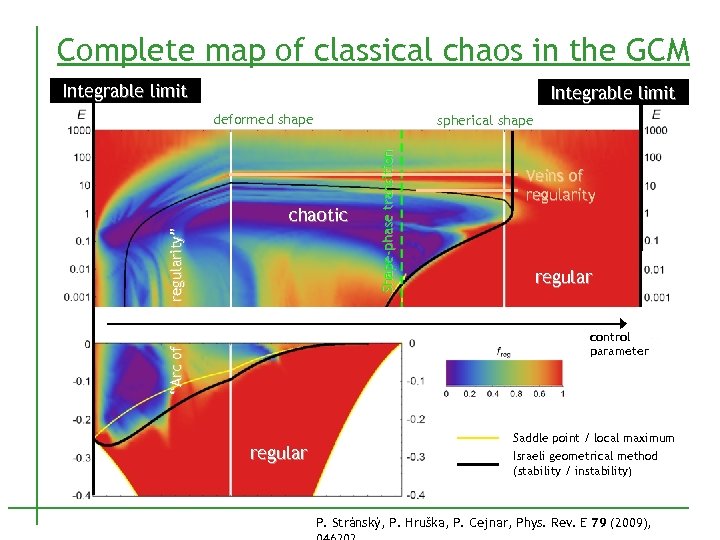Complete map of classical chaos in the GCM Integrable limit deformed shape regularity” chaotic Shape-phase transition spherical shape Veins of regularity regular “Arc of control parameter regular Saddle point / local maximum Israeli geometrical method (stability / instability) P. Stránský, P. Hruška, P. Cejnar, Phys. Rev. E 79 (2009),

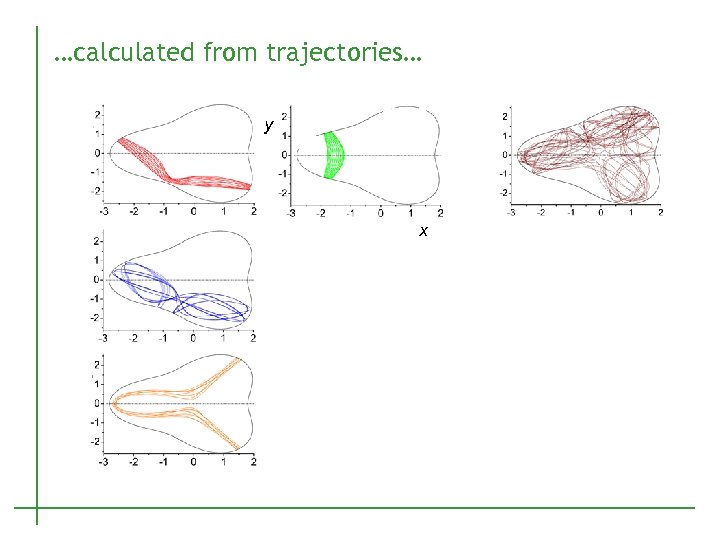…calculated from trajectories… y x

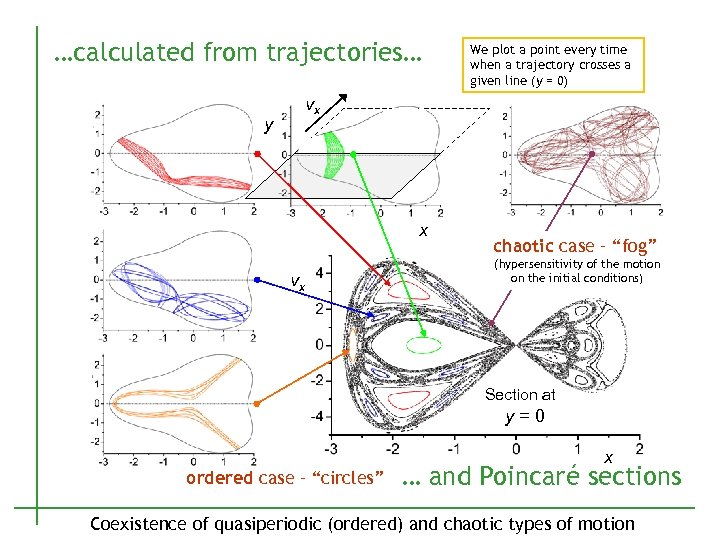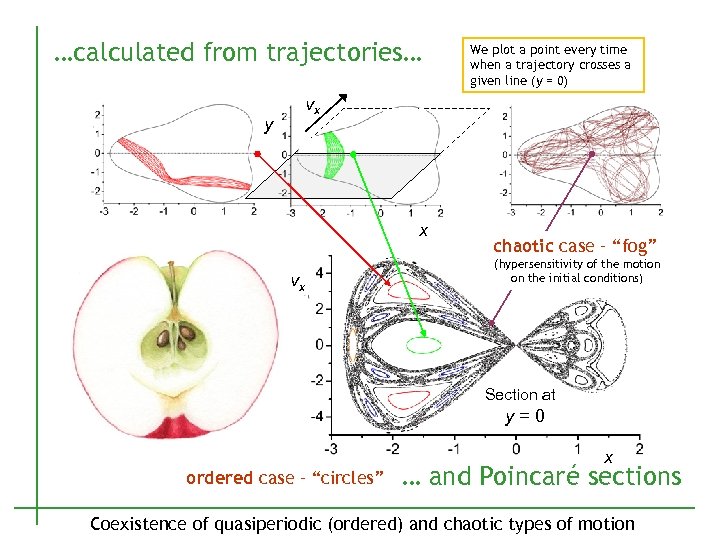…calculated from trajectories… y We plot a point every time when a trajectory crosses a given line (y = 0) vx x vx chaotic case – “fog” (hypersensitivity of the motion on the initial conditions) Section at y=0 ordered case – “circles” x … and Poincaré sections Coexistence of quasiperiodic (ordered) and chaotic types of motion

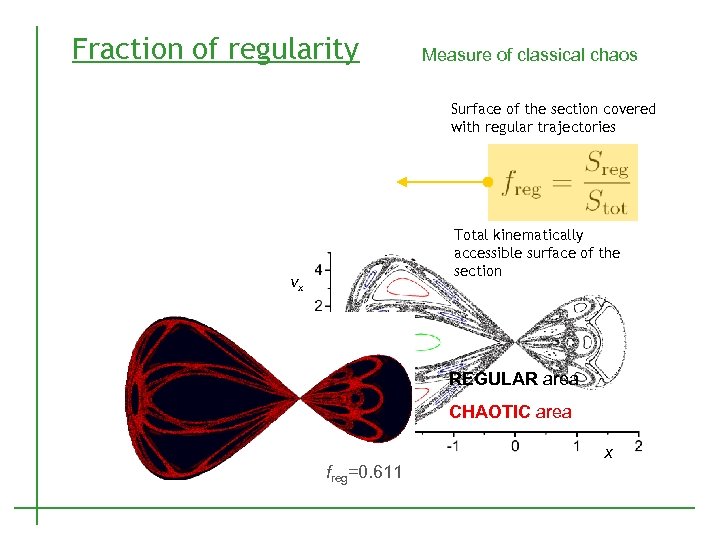Fraction of regularity Measure of classical chaos Surface of the section covered with regular trajectories Total kinematically accessible surface of the section vx REGULAR area CHAOTIC area freg=0. 611 x

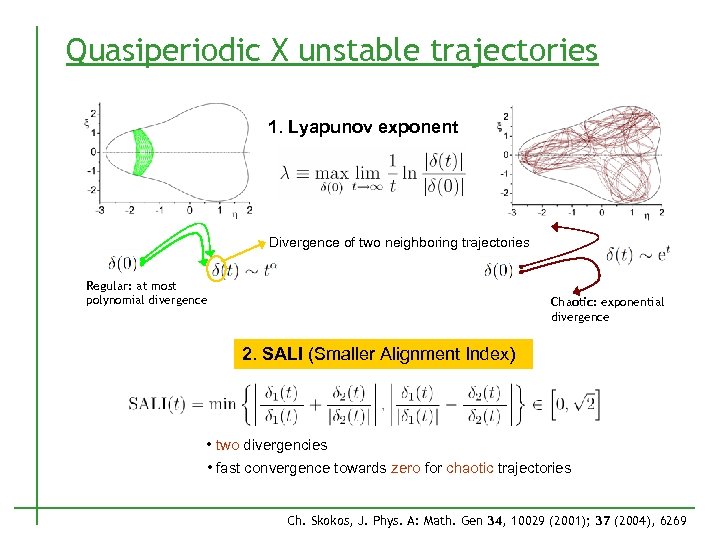Quasiperiodic X unstable trajectories 1. Lyapunov exponent Divergence of two neighboring trajectories Regular: at most polynomial divergence Chaotic: exponential divergence 2. SALI (Smaller Alignment Index) • two divergencies • fast convergence towards zero for chaotic trajectories Ch. Skokos, J. Phys. A: Math. Gen 34, 10029 (2001); 37 (2004), 6269

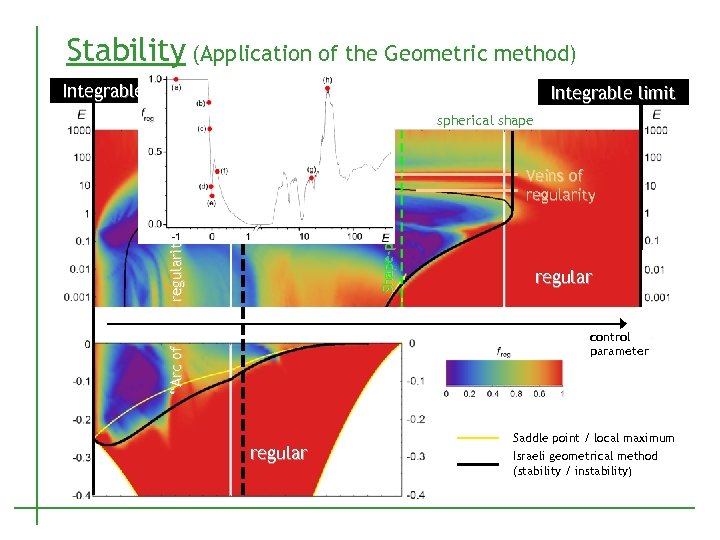Stability (Application of the Geometric method) Integrable limit deformed shape Shape-phase transition regularity” chaotic spherical shape Veins of regularity regular “Arc of control parameter regular Saddle point / local maximum Israeli geometrical method (stability / instability)

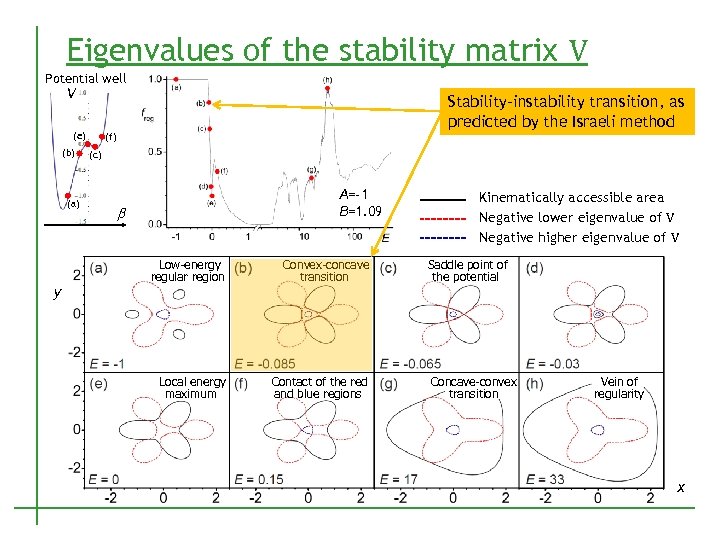Eigenvalues of the stability matrix V Potential well V Stability-instability transition, as predicted by the Israeli method (e) (b) (a) y (f) (c) A=-1 B=1. 09 b Low-energy regular region Convex-concave transition Local energy maximum Contact of the red and blue regions Kinematically accessible area Negative lower eigenvalue of V Negative higher eigenvalue of V Saddle point of the potential Concave-convex transition Vein of regularity x

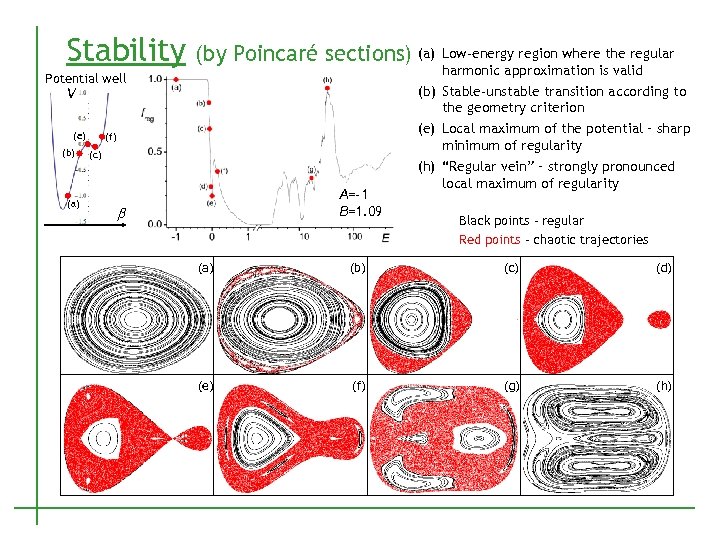Stability (by Poincaré sections) (a) Potential well V (e) (b) (a) (f) (c) A=-1 B=1. 09 b Low-energy region where the regular harmonic approximation is valid (b) Stable-unstable transition according to the geometry criterion (e) Local maximum of the potential – sharp minimum of regularity (h) “Regular vein” – strongly pronounced local maximum of regularity Black points – regular Red points – chaotic trajectories (a) (b) (c) (d) (e) (f) (g) (h)

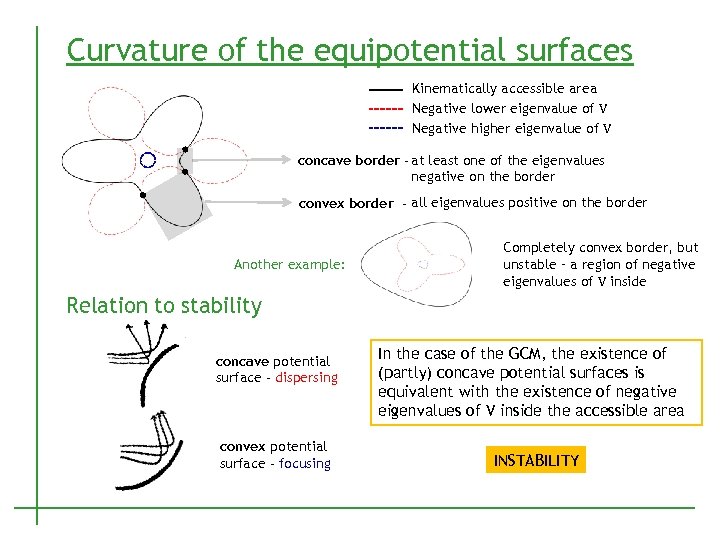Curvature of the equipotential surfaces Kinematically accessible area Negative lower eigenvalue of V Negative higher eigenvalue of V concave border - at least one of the eigenvalues negative on the border convex border - all eigenvalues positive on the border Another example: Completely convex border, but unstable – a region of negative eigenvalues of V inside Relation to stability concave potential surface - dispersing convex potential surface - focusing In the case of the GCM, the existence of (partly) concave potential surfaces is equivalent with the existence of negative eigenvalues of V inside the accessible area INSTABILITY

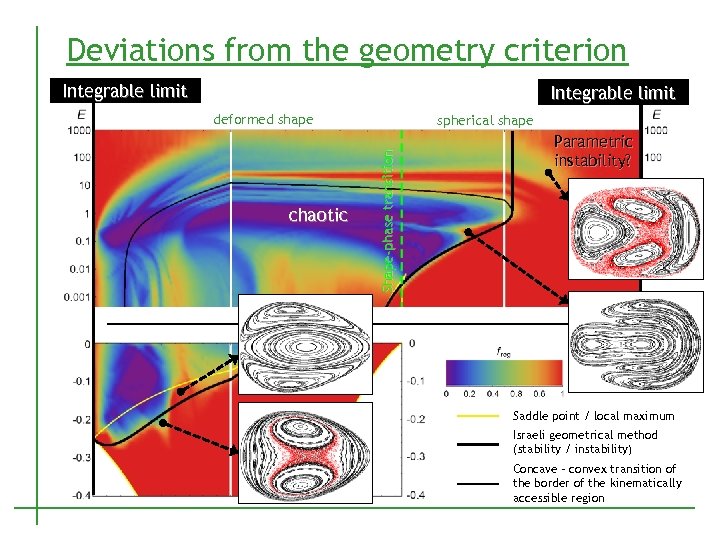Deviations from the geometry criterion Integrable limit deformed shape Shape-phase transition chaotic spherical shape Parametric instability? control parameter Saddle point / local maximum regular Israeli geometrical method (stability / instability) Concave – convex transition of the border of the kinematically accessible region

Conclusions: 1. The “Israeli geometry criterion” gives a fast indicator of stability of a Hamiltonian system without the need of solving equations of motion. In the GCM it exactly corresponds to the curvature of equipotential surfaces. 2. This indicator, although only approximate, works well in many physical systems: L. Horwitz et al. , Phys. Rev. Lett. 98, 234301 (2007) [2 D Toda lattice] Y. B. Zion and L. Horwitz, Phys. Rev. E 76, 046220 (2007) [3 D Yang-Mills system] Y. B. Zion and L. Horwitz, Phys. Rev. E 78, 036209 (2008) [2 D coupled HO, 2 D quartic oscillator] J. Li and S. Zhang, J. Phys. A: Math. Theor. 43, 125105 (2010 [Dicke model] A list of counterexamples is given in X. Wu, J. Geom. Phys. 59, 1357 (2009). However, the systems presented there are not bound. 3. The complete study of the dynamics in the GCM shows only small deviations from the criterion (chaotic dynamics penetration into stable region, completely regular appearing in unstable region). These deviations may be caused by an effect similar to the Parametric instability. The Riemannian geometry indicator gives a good estimate on the stability, but it does not capture the full richness of the inner dynamics of a Hamiltonian system.

Conclusions: 1. The “Israeli geometry criterion” gives a fast indicator of stability of a Hamiltonian system without the need of solving equations of motion. In the GCM it exactly corresponds to the curvature of equipotential surfaces. 2. This indicator, although only approximate, works well in many physical systems: L. Horwitz et al. , Phys. Rev. Lett. 98, 234301 (2007) [2 D Toda lattice] Y. B. Zion and L. Horwitz, Phys. Rev. E 76, 046220 (2007) [3 D Yang-Mills system] Y. B. Zion and L. Horwitz, Phys. Rev. E 78, 036209 (2008) [2 D coupled HO, 2 D quartic oscillator] J. Li and S. Zhang, J. Phys. A: Math. Theor. 43, 125105 (2010 [Dicke model] A list of counterexamples is given in X. Wu, J. Geom. Phys. 59, 1357 (2009). However, the systems presented there are not bound. 3. The complete study of the dynamics in the GCM shows only small deviations from the criterion (chaotic dynamics penetration into stable region, completely regular appearing in unstable region). These deviations may be caused by an effect similar to the Parametric instability. The Riemannian geometry indicator gives a good estimate on the stability. However, it does not capture the full richness of the inner dynamics of a Hamiltonian system. THANK YOU FOR YOUR And special thanks to Roelof Bijker, Octavio ATTENTIONorganizers of ELAF 2013 Castaños and all the