Резонанс токов и напряжений n Различают два

Резонанс токов и напряжений

n Различают два вида резонанса: резонанс токов и резонанс напряжений. Резонанс в последовательном контуре n Входное сопротивление такой цепи: n Условие наступления резонанса X= XL—XC=0. Поэтому резонанс в n такой цепи наступает, когда XL=XC, или

n При этом значения противоположных по фазе напряжений на индуктивности и емкости равны. Поэтому такой резонанс называют резонансом напряжений. Полное сопротивление цепи, по аналогии с полной мощностью: Резонансная частота: n или n Резонансными кривыми называются зависимости действующих или амплитудных значений тока и напряжения от частоты. n n

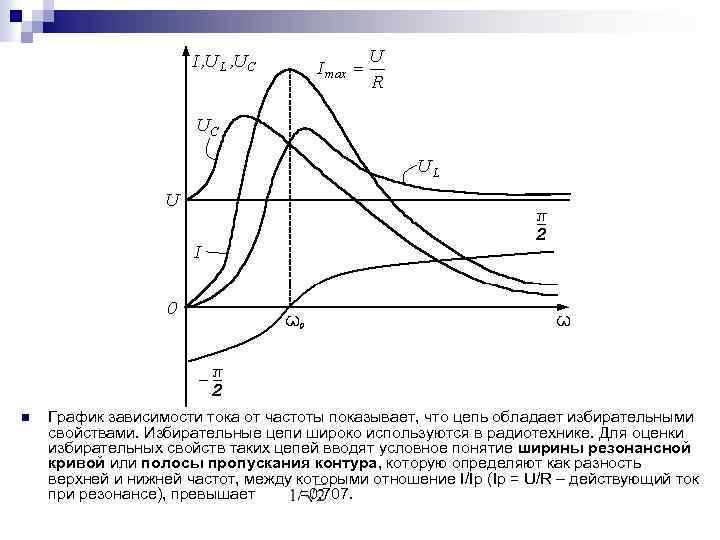n График зависимости тока от частоты показывает, что цепь обладает избирательными свойствами. Избирательные цепи широко используются в радиотехнике. Для оценки избирательных свойств таких цепей вводят условное понятие ширины резонансной кривой или полосы пропускания контура, которую определяют как разность верхней и нижней частот, между которыми отношение I/Ip (Ip = U/R – действующий ток при резонансе), превышает =0, 707.

n Добротность: n Полоса пропускания: n Характеристическое сопротивление: n или, с учетом ранее указанных соотношений, можно записать: n Зависимости от частоты параметров цепи называются частотными характеристиками.

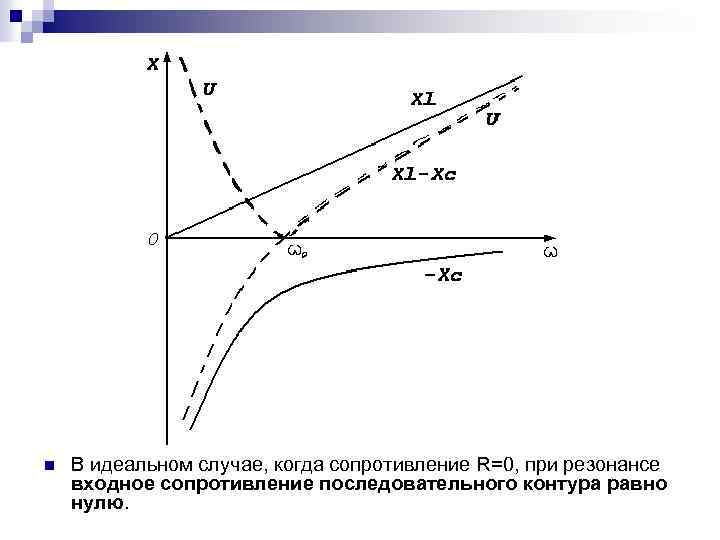n В идеальном случае, когда сопротивление R=0, при резонансе входное сопротивление последовательного контура равно нулю.

n Резонанс в параллельном контуре n Входное сопротивление такой цепи: n Видно, что такую цепь удобно рассматривать в терминах проводимости. Действительно, если сопротивление вещественно, то вещественна и проводимость этого сопротивления и наоборот. ; n Здесь знак «минус» перед мнимой частью появляется после домножения знаменателя сопротивления на комплексно сопряженное значение.

n Итак, условие резонанса будет выполнено в случае . n Получаем условие резонанса в параллельном контуре: n При резонансе в параллельном контуре противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название резонанса токов.

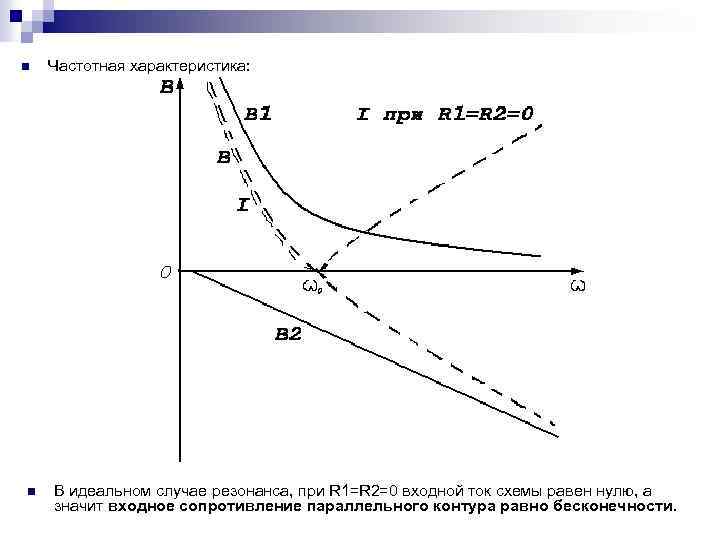n n Частотная характеристика: В идеальном случае резонанса, при R 1=R 2=0 входной ток схемы равен нулю, а значит входное сопротивление параллельного контура равно бесконечности.

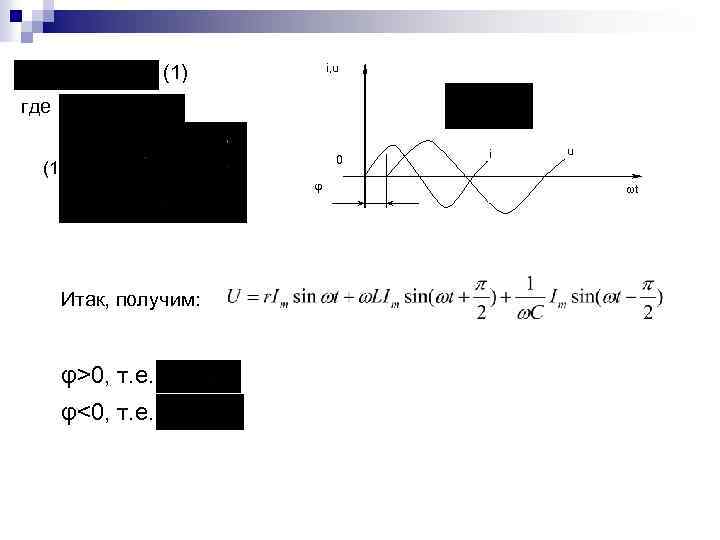i, u (1) где 0 (1) φ Итак, получим: φ>0, т. е. φ<0, т. е. i u ωt