РЕЗНИКОВ И. И. Лекция 6 План















 РЕЗНИКОВ И. И. Лекция 6
РЕЗНИКОВ И. И. Лекция 6
 План лекции: 1 Внутреннее трение (вязкость) жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости. 2 Ламинарное и турбулентное течение, число Рейнольдса. 3 Ламинарное течение жидкости в цилиндрических трубах. Формула Пуазейля. Гидравлическое сопротивление. 4 Распределение давления при течении реальной жидкости по трубам разного диаметра.
План лекции: 1 Внутреннее трение (вязкость) жидкости. Уравнение Ньютона. Ньютоновские и неньютоновские жидкости. 2 Ламинарное и турбулентное течение, число Рейнольдса. 3 Ламинарное течение жидкости в цилиндрических трубах. Формула Пуазейля. Гидравлическое сопротивление. 4 Распределение давления при течении реальной жидкости по трубам разного диаметра.
 1. ВНУТРЕННЕЕ ТРЕНИЕ ЖИДКОСТИ (ВЯЗКОСТЬ) При течении реальной Слои воздействуют жидкости отдельные её друг на друга. Так, слои воздействуют друг на например, третий слой друга с силами, стремится ускорить касательными к слоям. движение второго, но сам Это явление называют испытывает торможение с внутренним трением его стороны, а ускоряется или вязкостью. четвертым слоем и т. д. Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость.
1. ВНУТРЕННЕЕ ТРЕНИЕ ЖИДКОСТИ (ВЯЗКОСТЬ) При течении реальной Слои воздействуют жидкости отдельные её друг на друга. Так, слои воздействуют друг на например, третий слой друга с силами, стремится ускорить касательными к слоям. движение второго, но сам Это явление называют испытывает торможение с внутренним трением его стороны, а ускоряется или вязкостью. четвертым слоем и т. д. Сила внутреннего трения пропорциональна площади S взаимодействующих слоев и тем больше, чем больше их относительная скорость.
 Уравнение Ньютона для вязкой жидкости Fтр = η S • η (читается - эта) —коэффициент внутреннего трения, или динамическая вязкость. Вязкость зависит от температуры, давления и молекулярных свойств жидкости. - градиента скорости - изменение скорости в направлении х, перпендикулярном скорости, отнесенное к длине этого участка. S - площадь слоя. Размерности величин входящих в уравнение: [F] = H; [η] = = Па∙с (паскалъ-секунда), [] = ; [S] = м 2
Уравнение Ньютона для вязкой жидкости Fтр = η S • η (читается - эта) —коэффициент внутреннего трения, или динамическая вязкость. Вязкость зависит от температуры, давления и молекулярных свойств жидкости. - градиента скорости - изменение скорости в направлении х, перпендикулярном скорости, отнесенное к длине этого участка. S - площадь слоя. Размерности величин входящих в уравнение: [F] = H; [η] = = Па∙с (паскалъ-секунда), [] = ; [S] = м 2
 Примеры значений вязкости: ηводы = 1, 002∙ 10 -3 Па∙с, при t = 20 о С, а при t = 90 o. С ηводы = 0, 315∙ 10 -3 Па∙с. η подсолничного масла ≈ 55∙ 10 -3 Па∙с, при t = 20 о. С. Измерение вязкости производят с помощью специальных приборов называемых вискозиметрами.
Примеры значений вязкости: ηводы = 1, 002∙ 10 -3 Па∙с, при t = 20 о С, а при t = 90 o. С ηводы = 0, 315∙ 10 -3 Па∙с. η подсолничного масла ≈ 55∙ 10 -3 Па∙с, при t = 20 о. С. Измерение вязкости производят с помощью специальных приборов называемых вискозиметрами.
 2 Ламинарное и турбулентное течение
2 Ламинарное и турбулентное течение
 Увеличение скорости течения вязкой жидкости вследствие неоднородности давления по поперечному сечению трубы создает завихрения, и движение становится турбулентным. При турбулентном течении скорость частиц в каждом месте непрерывно и хаотически изменяется, движение является нестационарным.
Увеличение скорости течения вязкой жидкости вследствие неоднородности давления по поперечному сечению трубы создает завихрения, и движение становится турбулентным. При турбулентном течении скорость частиц в каждом месте непрерывно и хаотически изменяется, движение является нестационарным.
 • Число Рейнольдса величина безразмерная. • Если число Рейнольдса больше некоторого критического (Re > Reкp), то движение жидкости турбулентное, если меньше, то ламинарное. • Например, для гладких цилиндрических труб Reкp ≈ 2300. • Для крови Reкр = 2000. Для идеальной жидкости Reкр = ∞.
• Число Рейнольдса величина безразмерная. • Если число Рейнольдса больше некоторого критического (Re > Reкp), то движение жидкости турбулентное, если меньше, то ламинарное. • Например, для гладких цилиндрических труб Reкp ≈ 2300. • Для крови Reкр = 2000. Для идеальной жидкости Reкр = ∞.
 ФОРМУЛА ПУАЗЕЙЛЯ Формула выведена французским врачом и ученым Пуазейлем в 1840— 1842 гг. Установим, от каких факторов зависит объем Q жидкости, протекающей через горизонтальную трубу за единицу времени.
ФОРМУЛА ПУАЗЕЙЛЯ Формула выведена французским врачом и ученым Пуазейлем в 1840— 1842 гг. Установим, от каких факторов зависит объем Q жидкости, протекающей через горизонтальную трубу за единицу времени.
 Зависимость скорости слоев от их расстояния r от оси определяется выражением dv = - rdr Как видно из уравнения скорости слоев жидкости от расстояния их до оси трубы представляет параболическую зависимость.
Зависимость скорости слоев от их расстояния r от оси определяется выражением dv = - rdr Как видно из уравнения скорости слоев жидкости от расстояния их до оси трубы представляет параболическую зависимость.
 обозначим Выражение Х называется гидравлическим сопротивлением.
обозначим Выражение Х называется гидравлическим сопротивлением.
 - формула Пуазейля.
- формула Пуазейля.
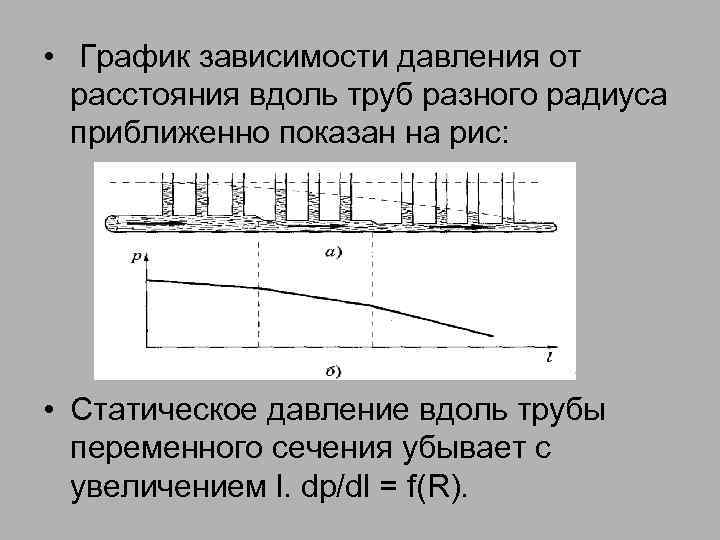
 • График зависимости давления от расстояния вдоль труб разного радиуса приближенно показан на рис: • Статическое давление вдоль трубы переменного сечения убывает с увеличением l. dp/dl = f(R).
• График зависимости давления от расстояния вдоль труб разного радиуса приближенно показан на рис: • Статическое давление вдоль трубы переменного сечения убывает с увеличением l. dp/dl = f(R).
 При рассмотрении движения крови, если крупный сосуд разветвляется на сосуды меньшего диаметра, то будет наблюдаться падение кровяного давления. Причем это падение в разветвленных сосудах больше, чем в крупных сосудах. Так, в артериях давление падает примерно на 20%, в артериолах на 50%, в капиллярах на 20%, в венах на 10%.
При рассмотрении движения крови, если крупный сосуд разветвляется на сосуды меньшего диаметра, то будет наблюдаться падение кровяного давления. Причем это падение в разветвленных сосудах больше, чем в крупных сосудах. Так, в артериях давление падает примерно на 20%, в артериолах на 50%, в капиллярах на 20%, в венах на 10%.
 ЛЕКЦИЯ № 7 Физические вопросы гемодинамики 1. Кровь как неньютоновская жидкость. 2. Механические свойства сосудов. Уравнение Ламе. 3. Пульсовая волна. 4. Модель кровообращения Франка. 5. Физические основы клинического метода измерения давления крови.
ЛЕКЦИЯ № 7 Физические вопросы гемодинамики 1. Кровь как неньютоновская жидкость. 2. Механические свойства сосудов. Уравнение Ламе. 3. Пульсовая волна. 4. Модель кровообращения Франка. 5. Физические основы клинического метода измерения давления крови.

