Reynolds Transport Theorem for Fluid Flows P M

Reynolds Transport Theorem for Fluid Flows P M V Subbarao Professor Mechanical Engineering Department I I T Delhi An Ulitmate Mathematical Frame Work to Create Fluid Flow Devices……

Reynolds : The Creator of Analogy Concept

Reynolds Analogy of First Kind • This establishes analogy between variation of field variable of a system considered as Control Mass and Control Volume. Also called as Reynolds Transport Theorem (RTT) RTT describes balance equation for field variable flowing through Control surfaces of a control volume.

Reynolds Transport Equation This Instantaneous Equation is valid for any system boundary with time the dependent volume V(t) and surface s(t). Also valid at initial time t = t 0 , where the volume V = VC and the surface s = s. C. VC and s. C are named as control volume and control surface. These control surfaces can be inlets or exits.

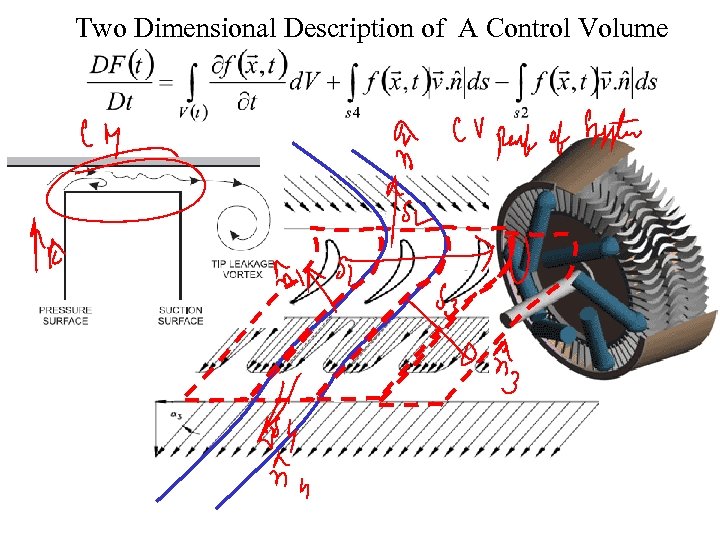Two Dimensional Description of A Control Volume

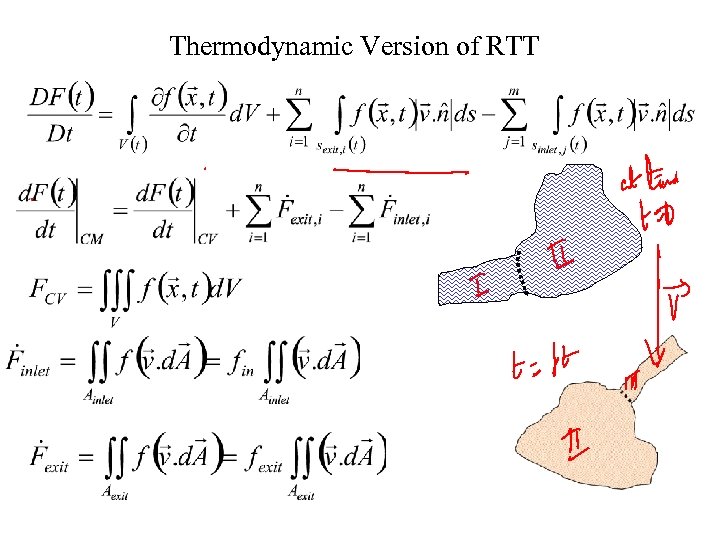Thermodynamic Version of RTT

Steady State Steady Flow Thermodynamic Model

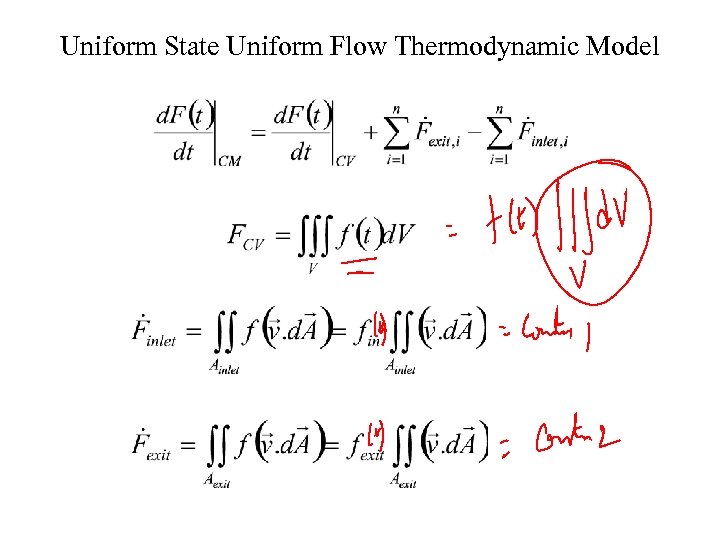Uniform State Uniform Flow Thermodynamic Model

Mass Flow Balance in Stationary Frame of Reference • The conservation law of mass requires that the mass contained in a material volume V=V(t), must be constant: Mass contained in a material volume Consequently, above equation requires that the substantial changes of the above mass must disappear:

Using this Reynolds transport theorem , the conservation of mass, results in: This integral is zero for any size and shape of material volume. Implies that the integrand in the bracket must vanish identically. The continuity equation for unsteady and compressible flow is written as: This Equation is a coordinate invariant equation. Its index notation in the Cartesian coordinate system given is:

Continuity Equation in Cylindrical Polar Coordinates • Many flows which involve rotation or radial motion are best described in Cylindrical Polar Coordinates. • In this system coordinates for a point P are r, and z. The velocity components in these directions respectively are vr , v and vz. Transformation between the Cartesian and the polar systems is provided by the relations,

The gradient operator is given by, As a consequence the conservation of mass equation becomes,

Continuity Equation in Cylindrical Polar Coordinates Spherical polar coordinates are a system of curvilinear coordinates that are natural for describing atmospheric flows. Define to be the azimuthal angle in the x-y plane from the x-axis with 0 < 2 . to be the zenith angle and colatitude, with 0 < r to be distance (radius) from a point to the origin. - The spherical coordinates (r, , ) are related to the Cartesian coordinates (x, y, z) by

Transformation Function for CCS to SCS The gradient is As a consequence the conservation of mass equation becomes,

Balance of Linear Momentum • The momentum equation in integral form applied to a control volume determines the integral flow quantities such as blade lift, drag forces, average pressure. • The motion of a material volume is described by Newton’s second law of motion which states that mass times acceleration is the sum of all external forces acting on the system. • These forces are identified as electrodynamic, electrostatic, and magnetic forces, viscous forces, gravitational forces …. • For a control mass This equation is valid for a closed system with a system boundary that may undergo deformation, rotation, expansion or compression.

Balance of Momentum for Fluid Flow • In a flow, there is no closed system with a defined system boundary. • The mass is continuously flowing from one point to another point. • Thus, in general, we deal with mass flow rate rather than mass. • Consequently, the previous equation must be modified in such a way that it is applicable to a predefined control volume with mass flow rate passing through it. • This requires applying the Reynolds transport theorem to a control volume.

The Preparation • The momentum balance for a CM needs to be modified, before proceeding with the Reynolds transport theorem. • As a first step, add a zero-term to CM Equation.

• Applying the Reynolds transport theorem to the left-hand side of Equation Replace the second volume integral by a surface integral using the Gauss conversion theorem

Fluid Flows using a selected combination of Forces • Systems only due to Body Forces. • Systems due to only normal surface Forces. • Systems due to both normal and tangential surface Forces. – Thermo-dynamic Effects (Buoyancy forces/surface)…. . – Physico-Chemical/concentration based forces (Environmental /Bio Fluid Mechanics)

Conservation Momentum for A CV

The Body Forces on A Fluid Flow • The body forces refer to long-ranged forces such as gravity or that arising from an electromagnetic field, and so on. • Such forces, as the name implies, vary slowly with the distance between interacting elements. • For instance, the gravitational force per unit mass acting on any object is very well represented by the constant vector g (|g| = 9. 806 m/s 2) for distances from the earth’s surface that are less than the order of the earth’s radius ( 6. 4 × 106 m). • A consequence of this slow variation is that such forces act equally on all the matter within an infinitesimal element of fluid continuum. • Thus, long-ranged forces manifest as body forces.

Extensive Nature of Body Forces • Assuming the body force per unit mass at a point x in the fluid, and at time t, to be (x, t). • The total force on an infinitesimal element around this point with volume d. V is given by ρ (x, t)d. V. • ρ is now the force per unit volume. • For gravity, this force is simply the weight of the element, ρgd. V. • For a conducting fluid in an magnetic field (B), the Lorentz force: L i×B • i is the current density.

The System of Body Forces in Fluid Flows • Gravitational Forces • Magnetic Forces (Magneto Hydrodynamic) – Lorentz force • Electrical forces. – Coulomb force – Dielectric force – Electrostriction

Flows Driven by Gravitational Force

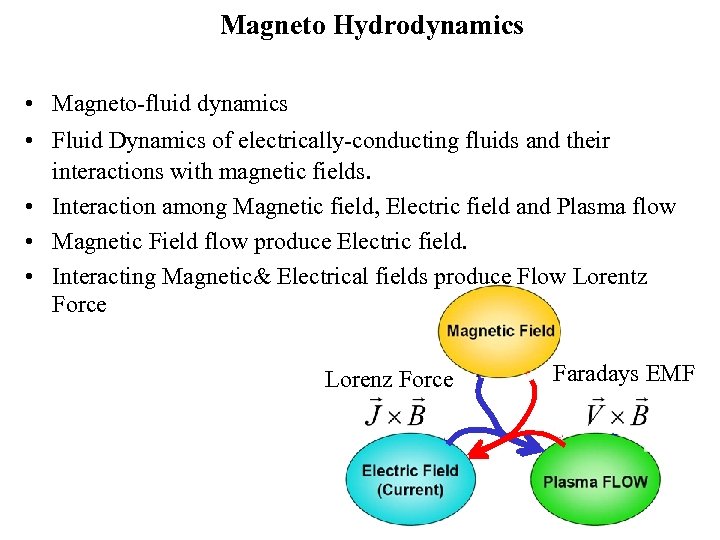Magneto Hydrodynamics • Magneto-fluid dynamics • Fluid Dynamics of electrically-conducting fluids and their interactions with magnetic fields. • Interaction among Magnetic field, Electric field and Plasma flow • Magnetic Field flow produce Electric field. • Interacting Magnetic& Electrical fields produce Flow Lorentz Force Lorenz Force Faradays EMF

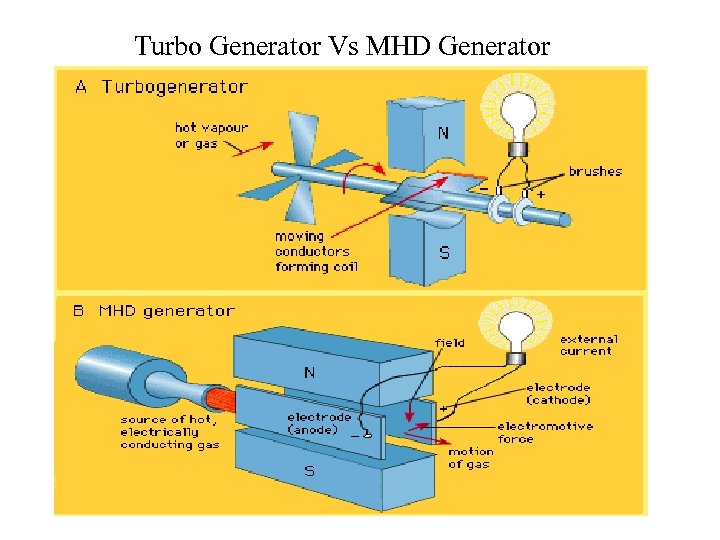Turbo Generator Vs MHD Generator

Important aspects of MDH 1. Accelerate fluids through Lorentz force, which refers to MHD accelerators. 2. Convert the kinetic energy of a fluid and its enthalpy into electric energy, which refers to MHD generators.

Principle of Operation • The underlying principle of MHD power generation is elegantly simple. • An electrically conducting fluid is energized by a primary energy source (e. g. , combustion of coal or a gas) and subject to a magnetic field. • This results in the establishment of an electromotive force within the conductor in accordance with the principle established by Faraday. • If the conducting fluid is an electrically conducting gas, it will expand. • Therefore the MHD system constitutes a heat engine involving an expansion from high to low pressure in a manner similar to that of a gas turbine.

• The gas turbine operates through the gas interaction with the surfaces of a rotating blade system. • The MHD system, however, involves a volume interaction between a gas and the magnetic field through which it is passing. • It is a system that depends on volume rather than surface interaction.

General Characteristics • The MHD generator can properly be viewed as an electromagnetic turbine. • Output is obtained from the conducting gas-magnetic field interaction directly in electrical form rather than in mechanical form. • Electrical conduction in gases occurs when electrons are available to be organized into an electric current in response to an applied or induced electric field. • The electrons may be either injected or generated internally, and, because of the electrostatic forces involved, they require the presence of corresponding positive charge from ions to maintain electrical neutrality.

• An electrically conducting gas consists in general of electrons, ions to balance the electric charge, and neutral atoms or molecules. • Such a gas is termed a plasma.

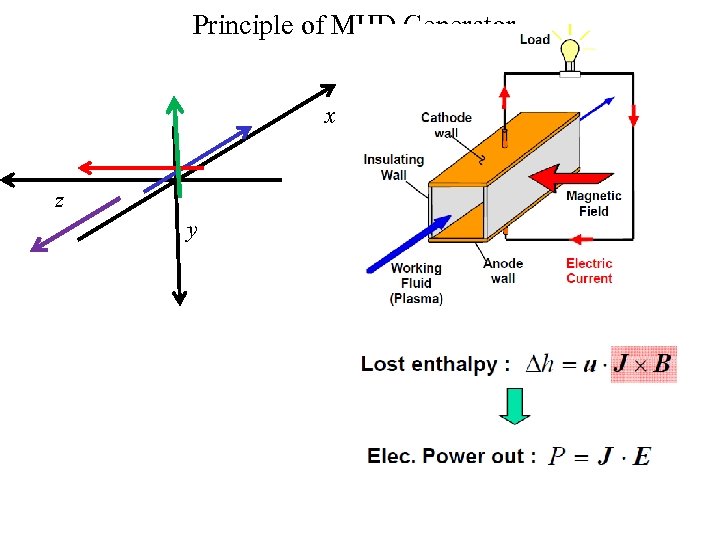Principle of MHD Generator x z y

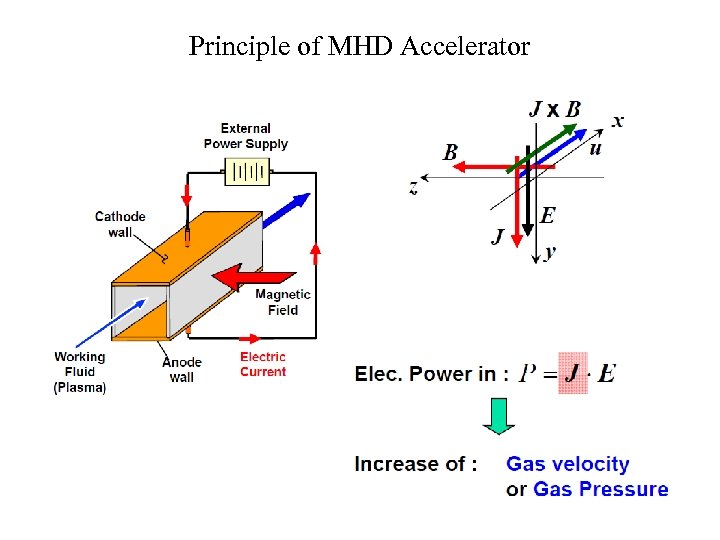Principle of MHD Accelerator

Development of Micro Pumps

Superiority of The Lorenz Force • • • Simple Structure Only MHD channel (electrodes, insulator) and Magnet High Power density ---- high electric field, current density Compact machine Small output applications High temperature operation ---- looking for suitable material No turbine, and no rotating machine Ceramic material can be used No moving parts No turbine and no rotating generator Good for space applications

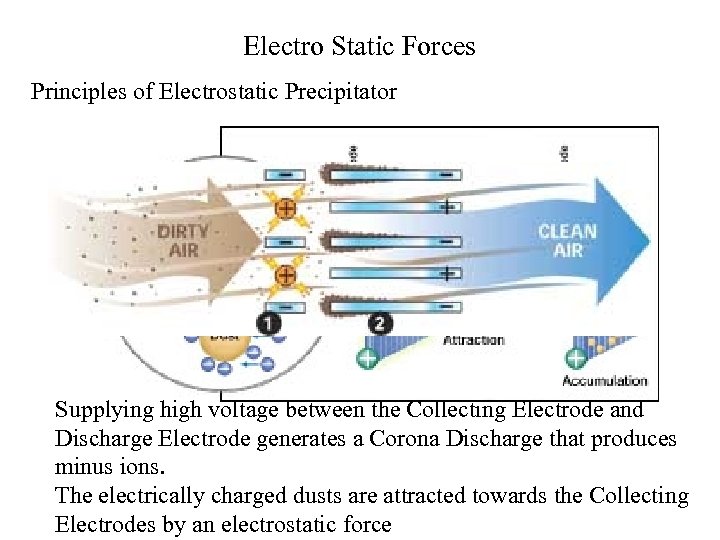Electro Static Forces Principles of Electrostatic Precipitator Supplying high voltage between the Collecting Electrode and Discharge Electrode generates a Corona Discharge that produces minus ions. The electrically charged dusts are attracted towards the Collecting Electrodes by an electrostatic force

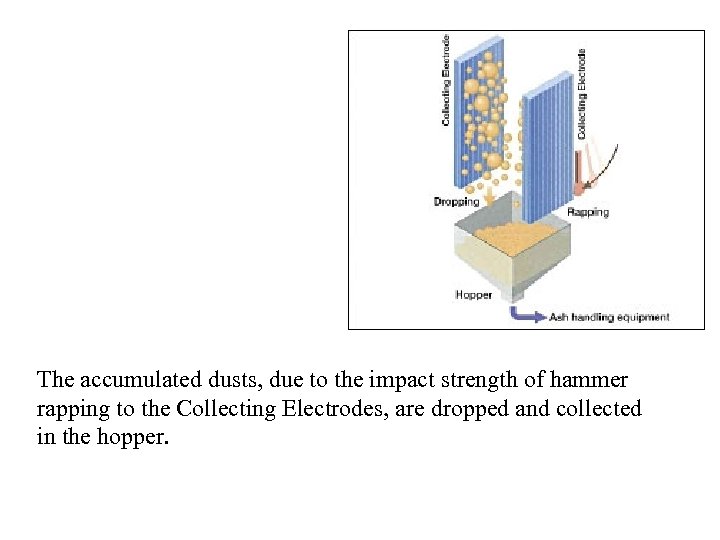The accumulated dusts, due to the impact strength of hammer rapping to the Collecting Electrodes, are dropped and collected in the hopper.

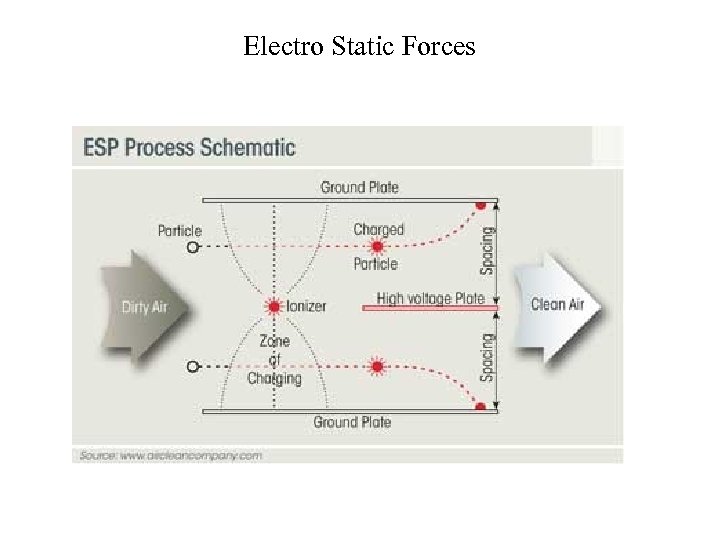Electro Static Forces