Reviewing Complex Flow Perpetuity If there is a

Reviewing Complex Flow Perpetuity If there is a mix of recurring and non-recurring or one-time cash flows that must be capitalized for perpetuity: 1. ) finding the NPW of all the one-time, nonrecurring cash flows (= CCPart 1 ) 2. ) finding the Annual Equivalent of one cycle of all the recurring cash flows, and then computing P (= CCPart 2) from the perpetuity relationship A = P(i) 3. ) summing (1. ) and (2. ) to find the total capitalized cost: CCTotal = CCPart 1 + CCPart 2 1

Perpetuity Example A new football stadium will replace the current municipal stadium at an initial cost of $250 million. One year later, the old stadium will be demolished at a net cost of $1. 5 million. Annual maintenance is expected to be $900 000, and every 15 years the skyboxes will be remodeled at a cost of $500 000. Find the capitalized cost if the discount rate is 10%, compounded annually. 2

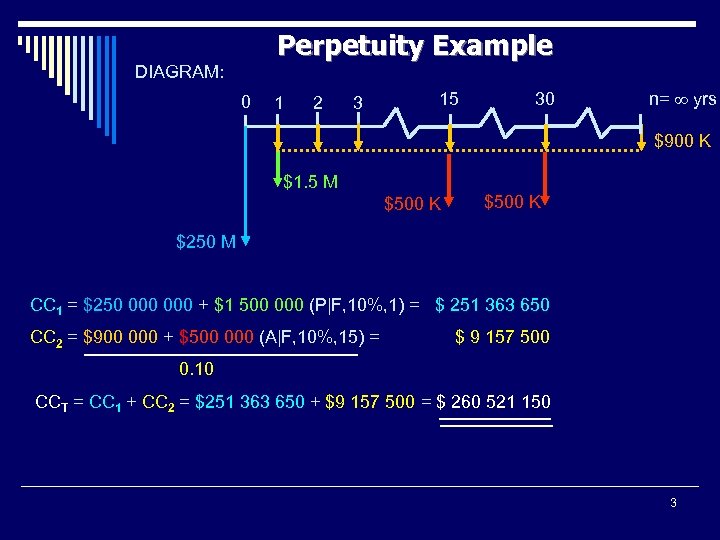Perpetuity Example DIAGRAM: 0 1 2 3 15 30 n= yrs $900 K $1. 5 M $500 K $250 M CC 1 = $250 000 + $1 500 000 (P|F, 10%, 1) = $ 251 363 650 CC 2 = $900 000 + $500 000 (A|F, 10%, 15) = $ 9 157 500 0. 10 CCT = CC 1 + CC 2 = $251 363 650 + $9 157 500 = $ 260 521 150 3

Reviewing…NPW Two approaches to handle differing project lives: Common Multiple Period: Projects are assumed to be repeated until a common multiple point in time is established. Study Period: Select a study period for both projects and estimate cash flows to conform to the study period. 4

Equivalent Annual Worth Analysis Equivalent Annual Worth (EAW) can be used to compare projects. Equivalent Annual Cost (EAC) can be used instead of EAW if revenues are not included. EAC = – EAW 5

Equivalent Annual Worth Analysis EAW and Types of Projects: • Revenue projects are expected to make money at a rate at least as high as the MARR, so select largest EAW that is 0. • Service projects are “have to do” situations, so select largest EAW (lowest EAC). 6

Capital Cost Recovery For a capital purchase (P) with a salvage value (S), the EAC can be calculated two ways: 1. P(A/P, i, n) – S (A/F, i, n) 2. (P – S) (A/P, i, n) + S( i ) Annual equivalent for loss of value Opportunity cost 7

Capital Cost Recovery Land is considered to have infinite life; it can be sold for its purchase price (neglecting inflation). P = S and EAC = S*i 8

Example 1 The Ragweed Pollination Company needs a new building to expand seed production. The building will cost $600, 000, last for 30 years, and is expected to sell for $100, 000. It will be built on property that costs $200, 000, which will be sold with the building. Energy costs are projected to be $45, 000 the first year increasing by $3, 000 each year after that. Needed equipment will cost $70, 000 and last 10 years with no salvage value. It will be replaced with identical equipment 10 and 20 years from now. Annual maintenance is projected to be $20, 000. Determine the Equivalent Annual Cost (EAC) for the proposed expansion using a MARR of 18% compounded annually. 9

1 st Costs: 200 000 Land 600 000 Building 70 000 Increases: Replacements: 20 000 Maintenance 45 000 Annuals: Equipment Energy 3 000/yr Energy Equipment (yr 10) 70 000 Salvage: 70 000 Equipment (yr 20) MARR: FIND: Building (yr 30) 200 000 Lifetime: 100 000 Land 30 yrs 18%, cpd annually EAC (= – EAW) 10

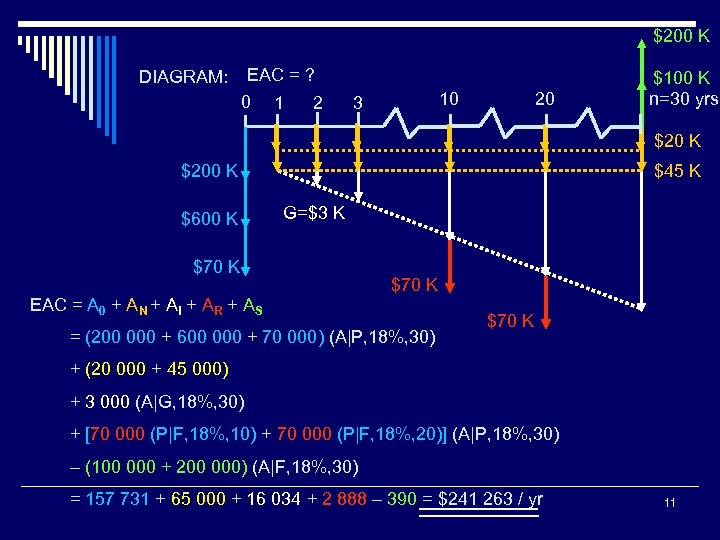$200 K EAC = ? DIAGRAM: 0 1 2 10 3 20 $100 K n=30 yrs $20 K $200 K $600 K $45 K G=$3 K $70 K EAC = A 0 + AN + AI + AR + AS $70 K = (200 000 + 600 000 + 70 000) (A|P, 18%, 30) $70 K + (20 000 + 45 000) + 3 000 (A|G, 18%, 30) + [70 000 (P|F, 18%, 10) + 70 000 (P|F, 18%, 20)] (A|P, 18%, 30) – (100 000 + 200 000) (A|F, 18%, 30) = 157 731 + 65 000 + 16 034 + 2 888 – 390 = $241 263 / yr 11

Example 2 A 1000 -foot tunnel must be constructed as part of a new aqueduct system for a major city. Two alternatives are being considered. One is to build a full-capacity tunnel now for $400, 000. The other alternative is to build a halfcapacity tunnel now for $200, 000, and then to build a second parallel half-capacity tunnel 20 years hence for $300, 000. The cost of repair of the tunnel lining at the end of every 10 years is estimated to be $20, 000 for the full capacity tunnel and $18, 000 for each half-capacity tunnel. Determine whether the full capacity tunnel or the halfcapacity tunnel should be constructed now. Solve the problem by annual worth analysis, using an interest rate of 6% per year compounded annually, and a 50 -year analysis period. (Note: There will be no tunnel lining repair at the end of the 50 years. ) 12

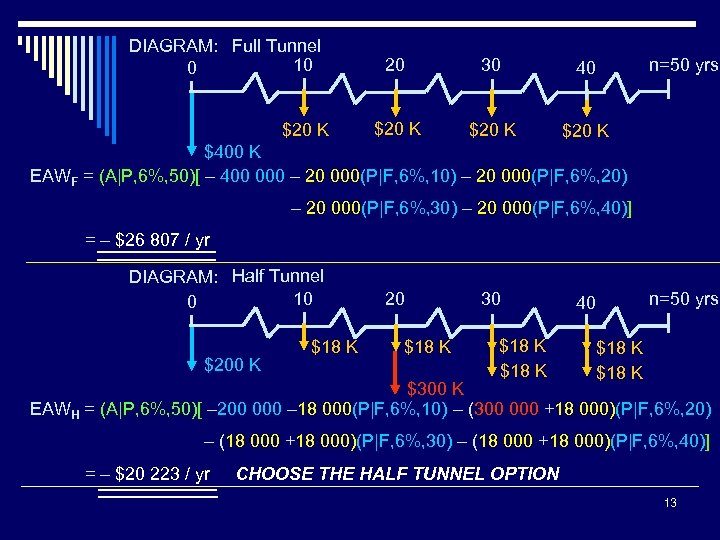DIAGRAM: Full Tunnel 10 0 $20 K 20 30 40 $20 K n=50 yrs $20 K $400 K EAWF = (A|P, 6%, 50)[ – 400 000 – 20 000(P|F, 6%, 10) – 20 000(P|F, 6%, 20) – 20 000(P|F, 6%, 30) – 20 000(P|F, 6%, 40)] = – $26 807 / yr DIAGRAM: Half Tunnel 10 0 $200 K $18 K 20 $18 K 30 $18 K 40 n=50 yrs $18 K $300 K EAWH = (A|P, 6%, 50)[ – 200 000 – 18 000(P|F, 6%, 10) – (300 000 +18 000)(P|F, 6%, 20) – (18 000 +18 000)(P|F, 6%, 30) – (18 000 +18 000)(P|F, 6%, 40)] = – $20 223 / yr CHOOSE THE HALF TUNNEL OPTION 13

Example 3 Your in-laws paid cash for a home they purchased 18 years ago for $100, 000. They just sold it for $100, 000. They were bragging that, neglecting such expenses as taxes, insurance, and utilities, it did not cost them anything to live in the house for the 18 years. Having just completed an engineering economics course as a part of your engineering degree, you knew immediately that your in-laws’ reasoning was incorrect. § Identify and describe the engineering economic principle involved. § Include in your explanation what it actually cost your in-laws each year to own the house provided that they value money at 6% per year compounded annually. (Do not include changes in the purchasing power of money, and continue to neglect taxes, maintenance, insurance and utilities) 14

What is the Engr Econ principle of Example 3? The economic principle is OPPORTUNITY COST: EAC = (P – S)(A|P, i, N) + S(i) = ($100 000 – $100 000)(A|P, 6%, 18) + $100 000(6%) = $0 + $6 000 = $6 000 / year to live in the house for each of the past 18 years. Effectively, you could tell your in-laws that if they had truly lived in the house for free, they could have spent $6 000 per year on better raising your spouse … … but then, again, maybe you shouldn’t. 15